1.算法概述

全局的能量函数公式如下: E(f)=Edata(f)+Esmooth(f) 其中,Edata 表示能量函数的数据项,意为该像素只考虑自身的视差值的倾向,不考虑邻域内其他像素的影响;N 表示匹配聚合时的支持窗口;p 表示图像中的一个像素点;dp∈D,D 表示视差取值范围;Dp(dp)表示 p 点的视差为 dp 时的匹配代价;Esmooth 表示能量函数的平滑项,平滑项反映了像素间视差值的影响关系。

针对全局立体匹配算法计算量大的问题,引入全局差错能量函数对算法进行改进.将全局差错能量函数作为立体匹配的匹配代价,同时进行跳跃式区域生长,隔点求取差错能量函数值以获取视差图,并采用均值滤波器对其做平滑处理,设置影响滤波阈值大小的容差系数,使之更适合人眼的观察.针对不同像素的彩色图像对,自适应选取容差系数得到较优的滤波后视差图.实验结果表明,改进算法在保证准确性的基础上可有效减小计算耗时,提高匹配实时性.

立体匹配算法步骤

1）匹配代价计算（Cost Computation）：

计算匹配代价，即计算参考图像上每个像素点IR(P)，以所有视差可能性去匹配目标图像上对应点IT(pd)的代价值，因此计算得到的代价值可以存储在一个h*w*d(MAX)的三维数组中，通常称这个三维数组为视差空间图（Disparity Space Image，DSI）。匹配代价时立体匹配的基础，设计抗噪声干扰、对光照变化不敏感的匹配代价，能提高立体匹配的精度。因此，匹配代价的设计在全局算法和局部算法中都是研究的重点。

2）代价聚合（Cost Aggregation）

通常全局算法不需要代价聚合，而局部算法需要通过求和、求均值或其他方法对一个支持窗口内的匹配代价进行聚合而得到参考图像上一点p在视差d处的累积代价CA(p,d)，这一过程称为代价聚合。通过匹配代价聚合，可以降低异常点的影响，提高信噪比（SNR,Signal Noise Ratio）进而提高匹配精度。代价聚合策略通常是局部匹配算法的核心，策略的好坏直接关系到最终视差图（Disparity maps）的质量。

3）视差计算（Disparity Computation）：

局部立体匹配算法的思想，在支持窗口内聚合完匹配代价后，获取视差的过程就比较简单。通常采用‘胜者为王’策略（WTA，Winner Take All）,即在视差搜索范围内选择累积代价最优的点作为对应匹配点，与之对应的视差即为所求的视差。即P点的视差为。

4）后处理（Post Process）

一般的，分别以左右两图为参考图像，完成上述三个步骤后可以得到左右两幅视差图像。但所得的视差图还存在一些问题，如遮挡点视差不准确、噪声点、误匹配点等存在，因此还需要对视差图进行优化，采用进一步执行后处理步骤对视差图进行修正。常用的方法有插值（Interpolation）、亚像素增强（Subpixel Enhancement）、精细化（Refinement）、图像滤波（Image Filtering）等操作。

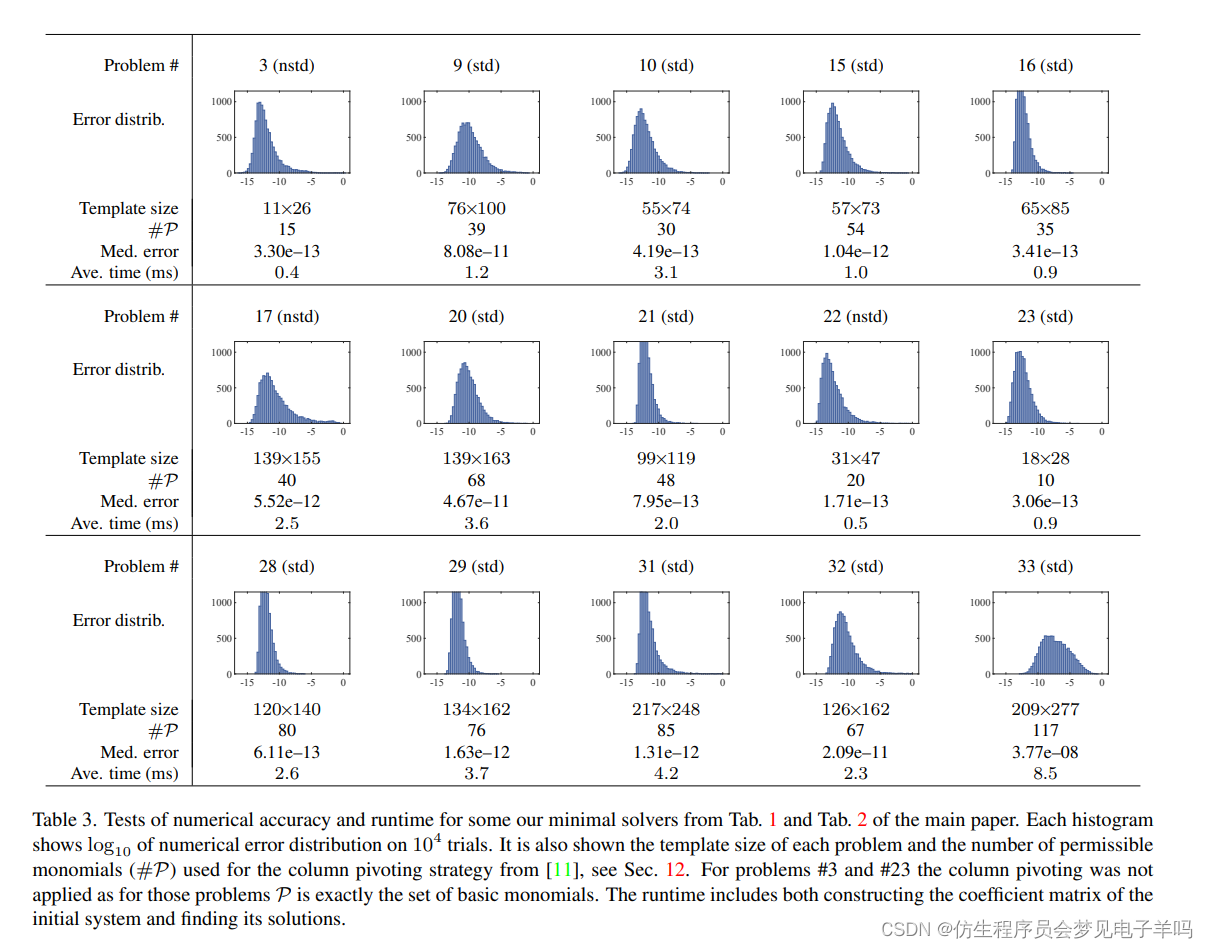
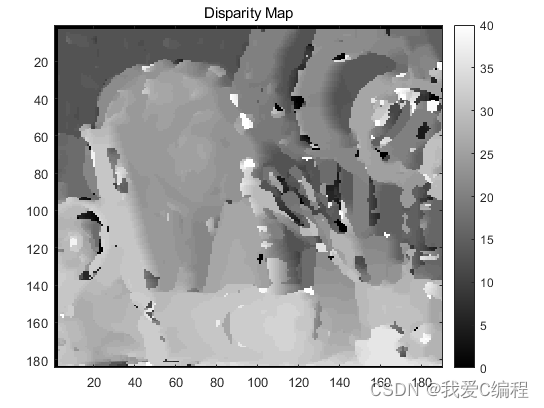
2.仿真效果预览

matlab2022a仿真结果如下：

3.核心MATLAB代码预览

% auto-presettings for the program
[m n p]=size(XR);
Edis=1000000*ones(m,n);
disparity=zeros(m,n);
XR=double(XR);
XL=double(XL);
 
% process by increasing disparity
for d=0:dmax
    fprintf ('Computing for disparity: %d\n',d);
% composing error energy matrix for every disparity.(Algorithm step:1)
for j=3+d:n-2
    for i=2:m-1
         if p==3
           %kareselfark(i,j-d)=(XR(i,j,1)-XL(i,j-d,1))^2+(XR(i,j,2)-XL(i,j-d,2))^2+(XR(i,j,3)-XL(i,j-d,3))^2;  
           if matching==1
           %point matching 
            ErrorEnergy(i,j-d)=(1/3)*[(XL(i,j,1)-XR(i,j-d,1))^2+(XL(i,j,2)-XR(i,j-d,2))^2+(XL(i,j,3)-XR(i,j-d,3))^2];
           elseif matching==2 
           %block matching with line type window
            ErrorEnergy(i,j-d)=(1/15)*[(XL(i,j,1)-XR(i,j-d,1))^2+(XL(i,j,2)-XR(i,j-d,2))^2+(XL(i,j,3)-XR(i,j-d,3))^2+(XL(i,j-1,1)-XR(i,j-1-d,1))^2+(XL(i,j-1,2)-XR(i,j-1-d,2))^2+(XL(i,j-1,3)-XR(i,j-1-d,3))^2+(XL(i,j+1,1)-XR(i,j+1-d,1))^2+(XL(i,j+1,2)-XR(i,j+1-d,2))^2+(XL(i,j+1,3)-XR(i,j+1-d,3))^2+(XL(i,j-2,1)-XR(i,j-2-d,1))^2+(XL(i,j-2,2)-XR(i,j-2-d,2))^2+(XL(i,j-2,3)-XR(i,j-2-d,3))^2+(XL(i,j+2,1)-XR(i,j+2-d,1))^2+(XL(i,j+2,2)-XR(i,j+2-d,2))^2+(XL(i,j+2,3)-XR(i,j+2-d,3))^2];
           else
               top=0;
               for k=i-1:i+1
                   for l=j-1:j+1
                     top=top+(XL(k,l,1)-XR(k,l-d,1))^2+(XL(k,l,2)-XR(k,l-d,2))^2+(XL(k,l,3)-XR(k,l-d,3))^2;  
                   end
               end
               ErrorEnergy(k,l-d)=(1/27)*top;
           end 
       else
           Disp('ERROR WARNING: Use RGB color image for stereo pair');
        end
    end
end
 
% filtering. (Algorithm step:2)
ErrorEnergyFilt=IterativeAveragingFilter(ErrorEnergy,1,[4 4]);
 
% selecting disparity which has minimum error energy.(Algorithm step:3)
[m1 n1]=size(ErrorEnergyFilt);
for k=1:m1
    for l=1:n1
       if Edis(k,l)>ErrorEnergyFilt(k,l)
            disparity(k,l)=d;
            Edis(k,l)=ErrorEnergyFilt(k,l);
        end        
    end
end
end
% clear 1000000 pre-setting in Edis
for k=1:m
    for l=1:n
       if Edis(k,l)==1000000
            Edis(k,l)=0;
        end        
    end
end
 
% extracting calculated zone
nx=n-dmax;
for k=2:m-1
    for l=2:nx-1
        disparityx(k,l)=disparity(k,l);
        %Edisx(k,l)=Edis(k,l);
        %regMapx(k,l)=regMap(k,l);
        XLx(k,l)=XL(k,l);
        XRx(k,l)=XR(k,l);
        top=0;
        for x=k-1:k+1
            for y=l-1:l+1
                top=top+(XL(x,y+disparity(k,l),1)-XR(x,y,1))^2+(XL(x,y+disparity(k,l),2)-XR(x,y,2))^2+(XL(x,y+disparity(k,l),3)-XR(x,y,3))^2;  
            end
        end
        Ed(k,l)=(1/27)*top;
    end
end
 
%calculates error energy treshold for reliablity of disparity
Toplam=0;
for k=1:m-1
    for l=1:nx-1
      Toplam=Toplam+Ed(k,l);       
    end
end
% Error threshold Ve
Ve=Alfa*(Toplam/((m-1)*(nx-1)));
 
EdReliable=Ed;
disparityReliable=disparityx;
Ne=zeros(m,nx);
for k=1:m-1
    for l=1:nx-1
       if Ed(k,l)>Ve
          % sets unreliable disparity to zero
          disparityReliable(k,l)=0;
          EdReliable(k,l)=0;
          Ne(k,l)=1; % indicates no-estimated state
        end        
    end
end
 
% calculating reliablities both raw disparity and filtered disparity
TopE=0;
TopER=0;
Sd=0;
for k=1:m-1
    for l=1:nx-1
          TopE=TopE+Ed(k,l);
          if Ne(k,l)==0          
             TopER=TopER+EdReliable(k,l);
             Sd=Sd+1;
          end          
    end
end
ReliablityE=((nx-1)*(m-1))/(TopE);
ReliablityER=(Sd)/(TopER);
 
% median filtering for repairment of occulations
%disparityF=IterativeAveragingFilter(disparity,5,[4 4]);
disparityF=medfilt2(disparityReliable,[5 5]);
 
for k=1:m-1
    for l=1:nx-1
          % Zero disparity produce zero dept
          if disparityF(k,l)<5;
              DepthMap(k,l)=0;
          else
              DepthMap(k,l)=foc*(T/disparityF(k,l));
        end        
    end
end
 
fprintf ('******** Reliablity Report  ********** \n')
fprintf ('Reliablity of the disparity map: %f \n',ReliablityE)
fprintf ('Reliablity of the disparity map filtered: %f \n',ReliablityER)
fprintf ('******** Algoritm Speed Report  ********** \n')
fprintf ('Time Spend for calculation: %f \n',toc)
 
figure(1)
imagesc(disparityx);colorbar;
colormap('gray')
title('Disparity Map')
% pixval on
 
figure(2)
colormap('gray')
imagesc(disparityReliable);colorbar;
title('Disparity Map with Reliable Disparities')
% pixval on
 
figure(3)
colormap('gray')
imagesc(disparityF);colorbar;
title('Median Filtered Disparity Map with Reliable Disparities')
% pixval on
A69