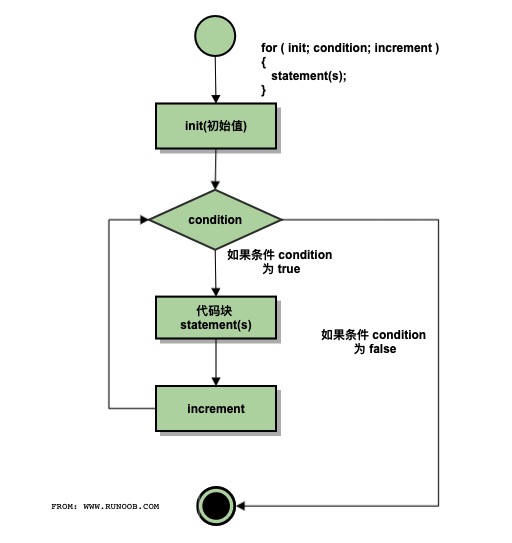
题目描述2
Problem - A - Codeforces 
题目分析
思路一:
由于是连续的数,我们可以使用f1, f2, f3来记录连续数的开头数字,只可能有三种情况
①开头数为第一个数-1
②开头数为第一个数
③开头数为第一个数+1
分别观察这三个情况,如果都不符合要求说明此只能记为NO
如果这三种情况有一种符号就记为YES
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 10;
void solve()
{
int flag1 = 0, flag2 = 0, flag3 = 0;
ll n, a[N];
cin >> n;
cin >> a[1];
ll f1 = a[1];
ll f2 = a[1] - 1;
ll f3 = a[1] + 1;
for(int i = 2; i <= n; i ++)
{
cin >> a[i];
}
for(int i = 1; i <= n; i ++)
{
if(f1 <= a[i] + 1 && f1 >= a[i] - 1)
{
f1 ++;
}
else
{
flag1 = 1;
}
}
for(int i = 1; i <= n; i ++)
{
if(f2 <= a[i] + 1 && f2 >= a[i] - 1)
{
f2 ++;
}
else
{
flag2 = 1;
}
}
for(int i = 1; i <= n; i ++)
{
if(f3 <= a[i] + 1 && f3 >= a[i] - 1)
{
f3 ++;
}
else
{
flag3 = 1;
}
}
if(flag1 == 1 && flag2 == 1 && flag3 == 1)cout << "NO" << '\n';
else cout << "YES" << '\n';
return;
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while(t --)
{
solve();
}
return 0;
}思路二:
由于是连续的一段,所以只能连续往左移或者连续往右移,最左边的只能向右移,最右边的只能向左移(这两个数的移动可以改变中间的空隙的大小,故最多空隙大小不能大于2)对于中间的数无论是向左移还是向右移都不能改变其真正中间空隙的大小
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
void solve()
{
int n, a[N];
int cnt = 0;
cin >> n;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
}
for(int i = 2; i <= n; i ++)
{
cnt += a[i] - a[i - 1] - 1;
}
if(cnt > 2)cout << "NO" << '\n';
else cout << "YES" << '\n';
}
int main()
{
int t;
cin >> t;
while(t --)
{
solve();
}
return 0;
}题目描述2
Problem - B - Codeforces

题目分析
我们可以假象使用一个数组c来描述了操作的情况,
ci < 0 表示 ci = -k * ai,也就是经行了k次的减ai的操作,
ci > 0 表示 ci = k * ai,也就是经行了k次的加ai的操作
ci = 0 表示没有经行任何的操作
我们发现操作一定是先减后加的为了使用最少的操作,也就是k最小,其中先减后加的操作中必有一个操作为0步,我们可以从每一步开始一一枚举为0的操作,最后从这个位置分别向左和向右计算出整个c数组,最后找出最小的操作即可

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5 + 10;
ll a[N], b[N], n;
int main()
{
ll ans = 8e18;
cin >> n;
for(ll i = 1; i <= n; i ++)cin >> a[i];
for(ll i = 1; i <= n; i ++)
{
ll cnt = 0;
memset(b, 0, sizeof b);
for(ll j = i - 1; j >= 1; j --)//向左
{
ll k = 1 - b[j + 1] / a[j];
b[j] = - k * a[j];
cnt += k;
}
for(ll j = i + 1; j <= n; j ++)//向右
{
ll k = 1 + b[j - 1] / a[j];
b[j] = k * a[j];
cnt += k;
}
ans = min(ans, cnt);
}
cout << ans;
return 0;
}题目描述3
Problem - C - Codeforces

题目分析
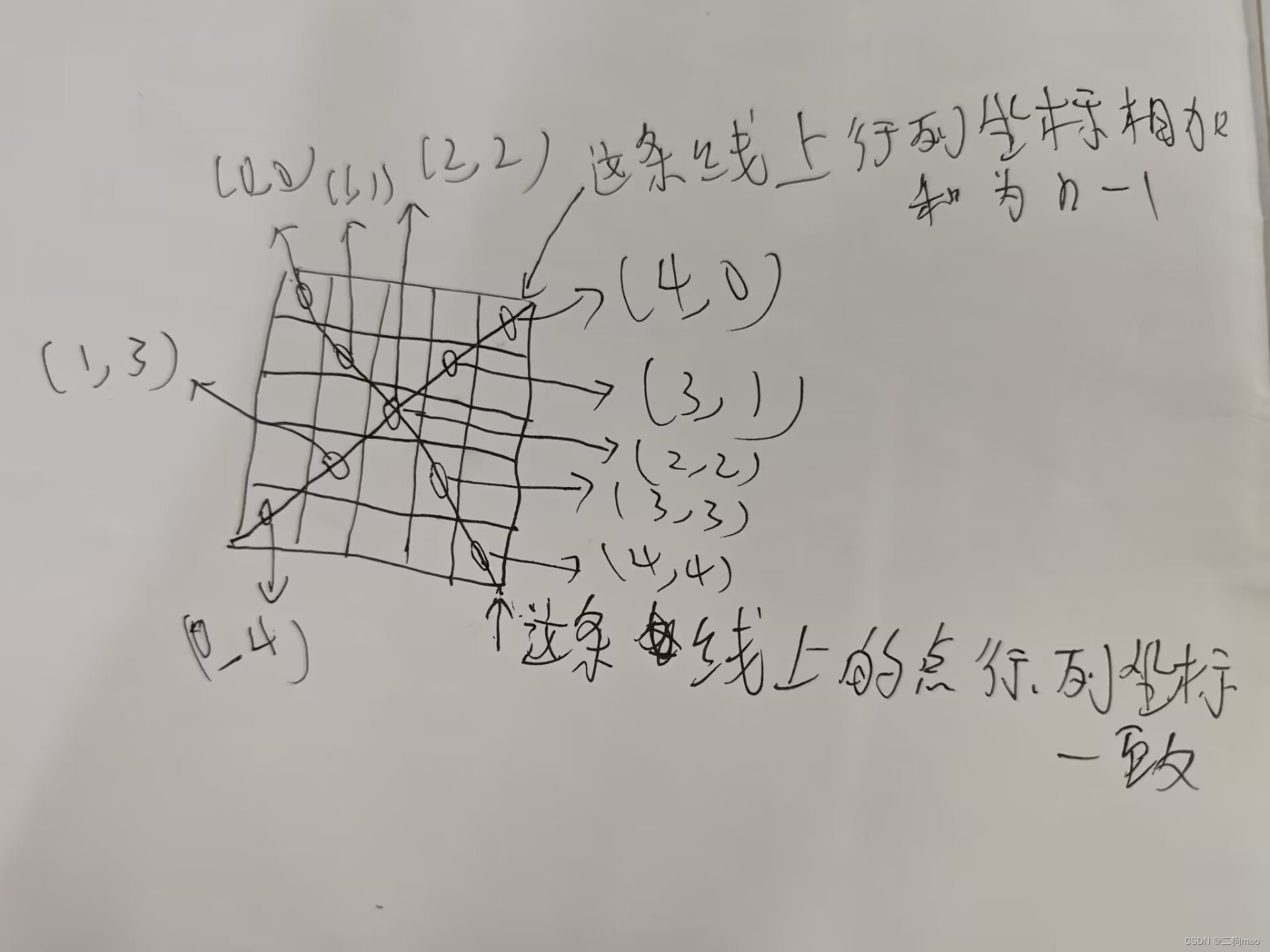
对于带有绝对值的,我们首先需要想到去掉绝对值或者说确定这个绝对值所代数的具体的正负号,对于构造问题,我们可以考虑顺序,逆序跳序
我们先思考顺序:12 34 56 78
这样由于第一部分全部为负,故我们逆序思考
87 65 43 21

通过上图我们发现在逆序过后每颠倒两个数就会多一个2,故序列得以构造
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, k, a[N];
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n >> k;
n = n * 2;
for(int i = 1; i <= n; i ++)a[i] = n - i + 1;
for(int i = 1; i <= k; i ++)swap(a[2 * i], a[2 * i - 1]);
for(int i = 1; i <= n; i ++)cout << a[i] << ' ';
return 0;
}题目描述4
Problem - D - Codeforces

题目分析

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e7 + 10, inf = 2e9;
int minp[N];
void euler(ll n)
{
bitset<N>vis;
vector<ll> primes;
vis[0] = vis[1] = true;
minp[1] = 1;
for(ll i = 2; i <= n; i ++)
{
if(!vis[i])primes.push_back(i),minp[i] = i;
for(int j = 0; j < primes.size() && i * primes[j] <= n; j ++)
{
vis[i * primes[j]] = true;
minp[i * primes[j]] = primes[j];
if(i % primes[j] == 0)break;
}
}
}
void solve()
{
ll x, y;
cin >> x >> y;
if(y - x == 1)cout << -1 << '\n';
else
{
ll ans = inf;
y-= x;
while(y > 1)
{
ll p = minp[y];
ans = min(ans, ((-x) % p + p) % p);
while(y % p == 0)y /= p;
}
cout << ans << '\n';
}
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
euler(1e7);
cin >> t;
while(t --)
{
solve();
}
return 0;
}题目描述5
Problem - A - Codeforces

题目分析
对于此题意是删除左右两端连续的串,使留下的0以及删除的1最大值最小最终只剩下一部分,我们可以使用双指针来枚举这一部分,c0 : 保留下来0的个数, c1 : 删除掉的1的个数,枚举左端点,当c0 == c1时右端点确定
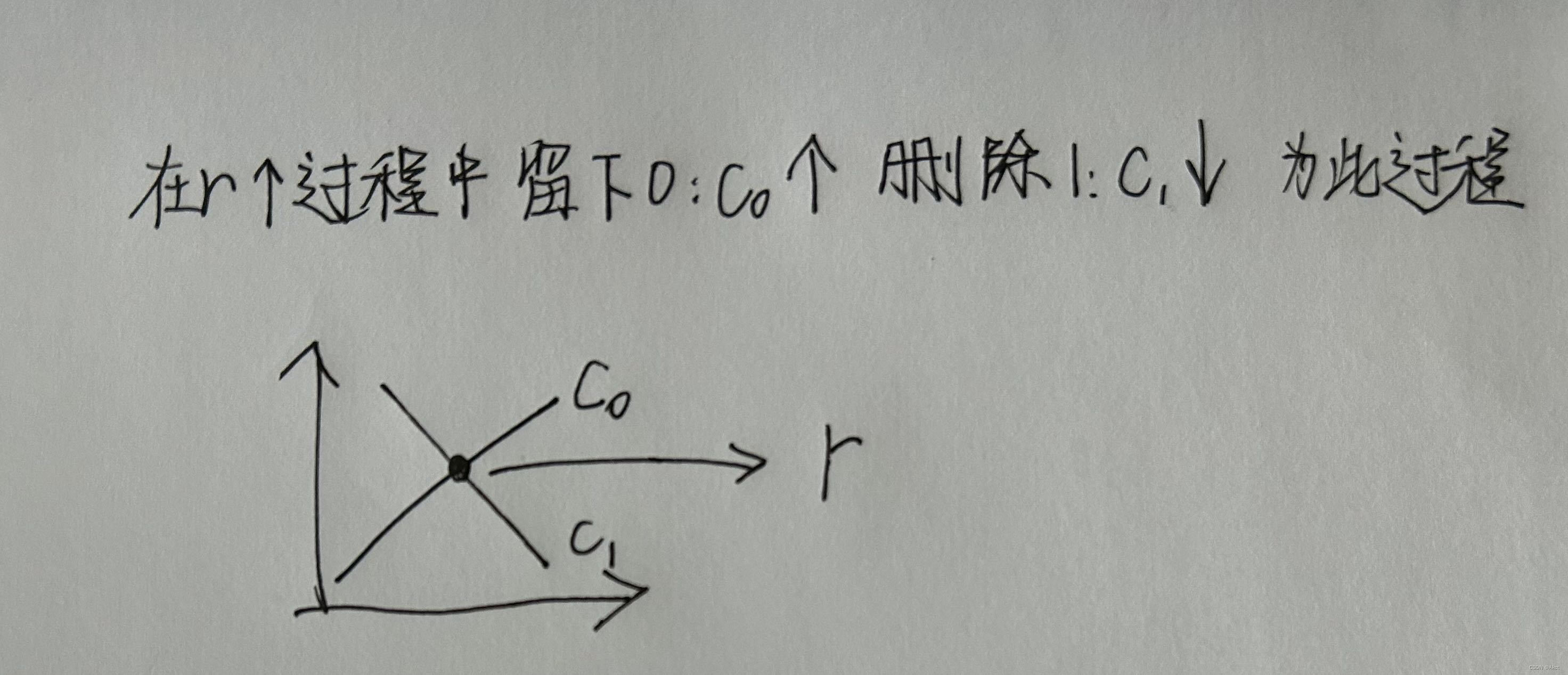
在这两个数发生变化的时候一方变化,另一方必定不变,故一定会出现相交的点此点即为答案,找出最小的即可
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
char s[N];
void solve()
{
int c1 = 0, c0 = 0, ans = 3e5 + 10;
cin >> s + 1;
int n = strlen(s + 1);
for(int i = 1; i <= n; i ++)if(s[i] == '1')c1 ++;
for(int i = 1, j = 0; i <= n; i ++)
{
while(j + 1 <= n && c0 < c1)
{
j ++;
if(s[j] == '0')c0 ++;
else c1 --;
}
ans = min(ans, max(c1, c0));
if(s[i] == '1')c1 ++;
else c0 --;
}
cout << ans << '\n';
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while(t --)
{
solve();
}
return 0;
}