实验四：回溯算法的设计与分析

news2024/11/23 13:25:12

某不知名学校大二算法课实验报告

题目来自力扣

第一题：幂集

力扣题目链接：幂集

题目描述：

幂集。编写一种方法，返回某集合的所有子集。集合中不包含重复的元素。

说明：解集不能包含重复的子集。

示例:

输入： nums = [1,2,3]

输出：

[

  [3],

  [1],

  [2],

  [1,2,3],

  [1,3],

  [2,3],

  [1,2],

  []

]

经典的递归实现指数型枚举的模板题

画出递归搜索树，一层一层递归回溯即可

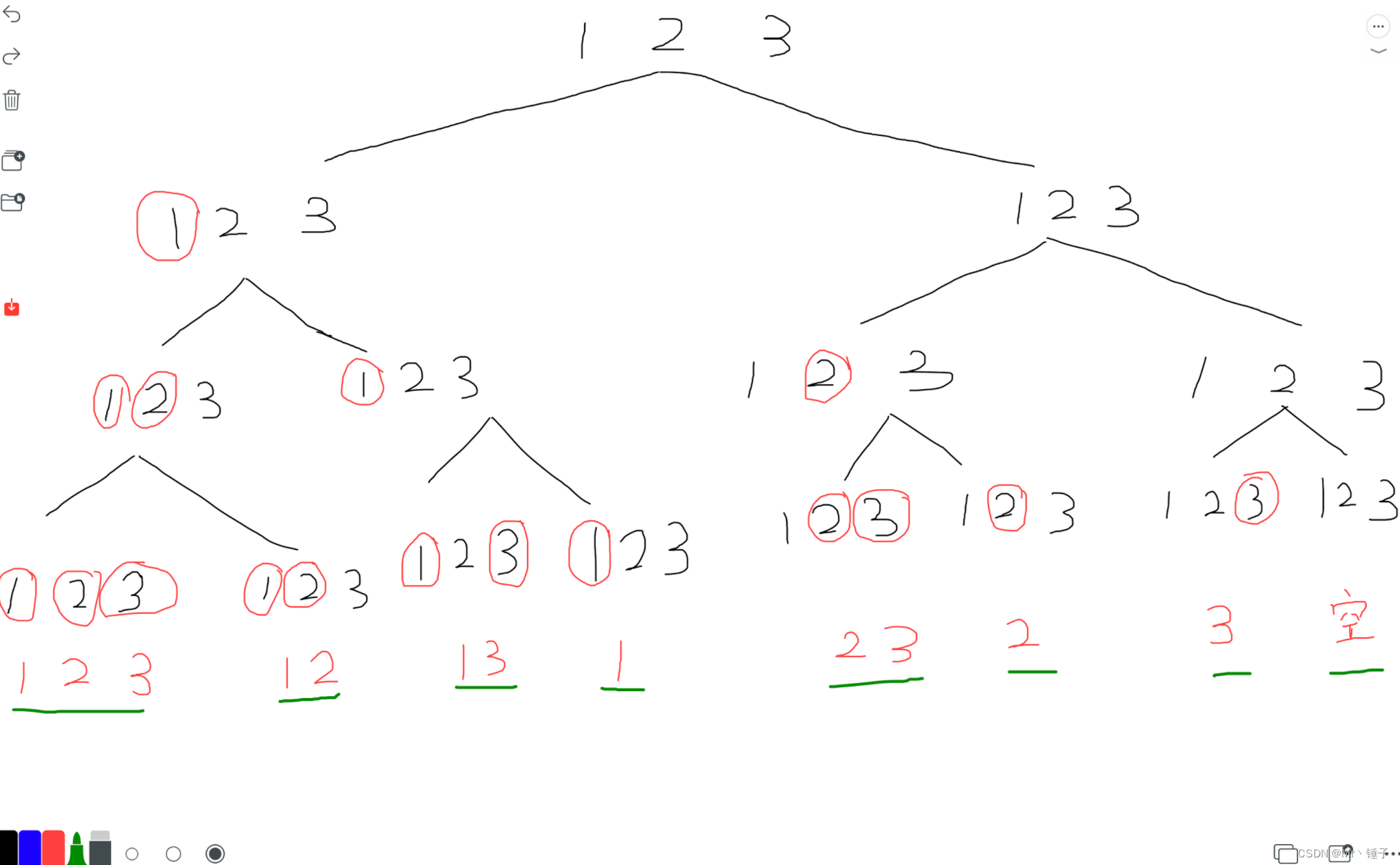注意每次要恢复现场

模板大体如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

注释＋代码如下：

class Solution {
public:
    
        vector<vector<int>>res; //答案
        vector<int>temp; //保存路径
        void dfs(vector<int>&nums, int value, int j) 
        {
            if(value == temp.size()) //选到最后一个数时
            {
                res.push_back(temp); //保存路径
            }
            for(int i = j ; i < nums.size(); i ++ )
            {
                temp.push_back(nums[i]);
                dfs(nums,value, i + 1);
                temp.pop_back();//还原现场
            }
        }
        vector<vector<int>> subsets(vector<int>& nums) {
            int n = nums.size();
            for(int i = 1; i <= n; i ++ )
            {
                dfs(nums, i , 0); // 传入数组，第几个数，已选第几个数
            }
            res.push_back(vector<int>{});
            return res;
    }
};

第二题：N皇后Ⅱ

力扣题目链接：N皇后Ⅱ

题目描述：

给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例:

输入: 4

输出: 2

解释: 4 皇后问题存在如下两个不同的解法。

[

[".Q..", // 解法 1

  "...Q",

  "Q...",

  "..Q."],

["..Q.", // 解法 2

  "Q...",

  "...Q",

  ".Q.."]

]

这道题居然是困难？这是一道非常非常经典的板子题，学习搜索必定会遇到的一道题

这题我的思路是通过行h搜索，cot，dg,udg分别标记列，对角线和反对角线

首先全部格子默认成'.'，枚举每一个位置能不能放‘Q’，符合条件则res ++ ;

代码＋注释如下：

class Solution {
public:
    //const int N = 10;
    bool cot[20], dg[20], udg[20];

    char g[20][20];
    int res;

    void dfs(int h,int n)
    {
        if( h == n) // 达到矩阵大小 答案加一
        {
            res ++ ;
            return;
        }
        for(int l = 0; l < n; l ++ )
        {
            //对角线h + l, 那么反对角线就是 n + h - l
            if(!cot[l] && !dg[h + l] && !udg[n + h - l])
            {
                g[h][l] = 'Q';
                cot[l] = dg[h + l] = udg[n + h - l] = true;
                dfs(h + 1, n);
                cot[l] = dg[h + l] = udg[n + h - l] = false;
                g[h][l] = '.';
            }
        }
    }
    int totalNQueens(int n) {
        for(int i = 0; i < n; i ++ )
        {
            for(int j = 0; j < n; j ++ )
            {
                g[i][j] = '.'; // 初始化
            }
        }
        dfs(0,n);
        return res;
    }
};

第三题：全排列

力扣题目链接：全排列

题目描述：

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]

输出:

[

  [1,2,3],

  [1,3,2],

  [2,1,3],

  [2,3,1],

  [3,1,2],

  [3,2,1]

]

这道题和第一题必须好好地对比学习，第一题是实现指数型枚举，这一题是实现排列型枚举

同样都是选不选的问题，同样都是递归搜索和回溯的问题，不过这会要多开一个数组保存路径

st数组标记有没有选过这个数字

代码如下：

class Solution {
public:
     vector<vector<int>>path;
     vector<int>temp;
     bool st[10];

    void dfs(int u, int n, vector<int>& nums)
    {
        if(temp.size() == n)
        {
            path.push_back(temp);
            return;
        }else
        {
            for(int i = 0; i < n; i ++ )
            {
                if(st[i] == false)
                {
                    st[i] = true;
                    temp.push_back(nums[i]);
                    dfs(u + 1, n, nums);
                    temp.pop_back();
                    st[i] = false;
                }
            }
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
       dfs(0, nums.size(), nums);
       return path;
    }
    
};

第四题：二进制手表

力扣题目链接：二进制手表

题目描述：

二进制手表顶部有 4 个 LED 代表 小时（0-11），底部的 6 个 LED 代表 分钟（0-59）。每个 LED 代表一个 0 或 1，最低位在右侧。

例如，下面的二进制手表读取 "4:51" 。

给你一个整数 turnedOn ，表示当前亮着的 LED 的数量，返回二进制手表可以表示的所有可能时间。你可以 按任意顺序 返回答案。

小时不会以零开头：

例如，"01:00" 是无效的时间，正确的写法应该是 "1:00" 。

分钟必须由两位数组成，可能会以零开头：

例如，"10:2" 是无效的时间，正确的写法应该是 "10:02" 。

示例 1：
输入：turnedOn = 1
输出：["0:01","0:02","0:04","0:08","0:16","0:32","1:00","2:00","4:00","8:00"]
示例 2：
输入：turnedOn = 9
输出：[]
提示：

0 <= turnedOn <= 10

思路：

构建一个可选择hour和minutes的数组，这里选择其实一共就是这10个bit，便于快速查找
递归时候就是看turnedOn是否被用完了，用完则返回结果；同时为了避免重复，每次遍历选择只选择当前序号后的数字；
剪枝：排除不允许的情况 hour<=11 和 minutes<=59

代码＋注释如下：

class Solution {
public:
    vector<string>res;

    void dfs(string& s, int start, int pointNum)
    {
        if(pointNum == 3)
        {
            if(isValid(s, start, s.size() - 1))
            {
                res.emplace_back(s);
            }
            return;
        }
        for(int i = start; i < s.size(); i ++ )
        {
            if(isValid(s, start, i)) {   
            s.insert(s.begin() + i + 1, '.'); // 插入点
            pointNum ++;
            dfs(s, i + 2, pointNum);
            pointNum -- ;
            s.erase(s.begin() + i + 1); //恢复现场
        } else break;
        }
    }

    bool isValid(string & s, int start, int end) 
    {
        if(start > end) 
        {
            return false;
        }
        if(s[start] == '0' && start != end) 
        {
            return false;
        }
        int num = 0;
        for(int i = start; i <= end; i ++ ) 
        {
            if(s[i] > '9' || s[i] < '0') 
            {
                return false;
            }
            num = num * 10 + (s[i] - '0');
            if(num > 255)
            {
                return false;
            }
        }
        return true;
    }
    vector<string> restoreIpAddresses(string s) {
        if(s.size() < 4 || s.size() > 12) return res;
        dfs(s, 0, 0);
        return res;
    }
};

第五题：复原ip地址

力扣题目链接：复原ip地址

题目描述：

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

有效的 IP 地址正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

例如："0.1.2.201" 和 "192.168.1.1" 是有效的 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是无效的 IP 地址。

示例 1：

输入：s = "25525511135"

输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"

输出：["0.0.0.0"]

示例 3：

输入：s = "1111"

输出：["1.1.1.1"]

示例 4：

输入：s = "010010"

输出：["0.10.0.10","0.100.1.0"]

示例 5：

输入：s = "101023"

输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

提示：

0 <= s.length <= 3000

s 仅由数字组成

切割问题，跟一道题切割回文子串很像，主要是检查函数isValid难写

搜索过程如下：

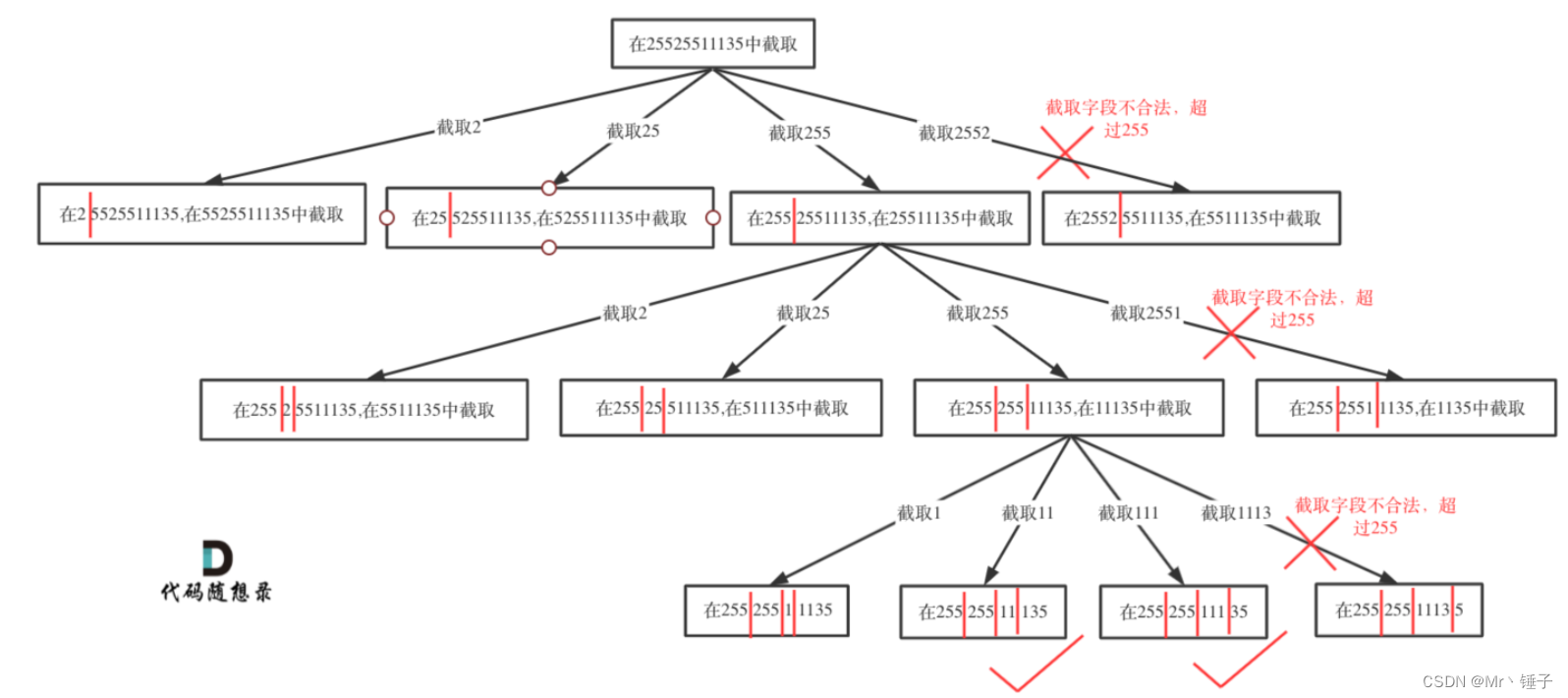
代码＋注释如下：

class Solution {
public:
    vector<string>res;

    void dfs(string& s, int start, int pointNum)
    {
        if(pointNum == 3) //3个点分4段
        {
            if(isValid(s, start, s.size() - 1))
            {
                res.emplace_back(s); //函数功能类似于push_back
            }
            return;
        }
        for(int i = start; i < s.size(); i ++ )
        {
            if(isValid(s, start, i)) {   
            s.insert(s.begin() + i + 1, '.'); // 插入点
            pointNum ++;
            dfs(s, i + 2, pointNum);
            pointNum -- ;
            s.erase(s.begin() + i + 1); //恢复现场
        } else break;
        }
    }

    bool isValid(string & s, int start, int end)  // 检查函数
    {
        if(start > end) 
        {
            return false;
        }
        if(s[start] == '0' && start != end) 
        {
            return false;
        }
        int num = 0;
        for(int i = start; i <= end; i ++ ) 
        {
            if(s[i] > '9' || s[i] < '0') 
            {
                return false;
            }
            num = num * 10 + (s[i] - '0');
            if(num > 255)
            {
                return false;
            }
        }
        return true;
    }
    vector<string> restoreIpAddresses(string s) {
        if(s.size() < 4 || s.size() > 12) return res;
        dfs(s, 0, 0);
        return res;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1098280.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！