LDA（Fisher）线性判别分析

对于二分类问题若存在一个$y_i=W{x}_i$将样本$X$投影到一维空间上

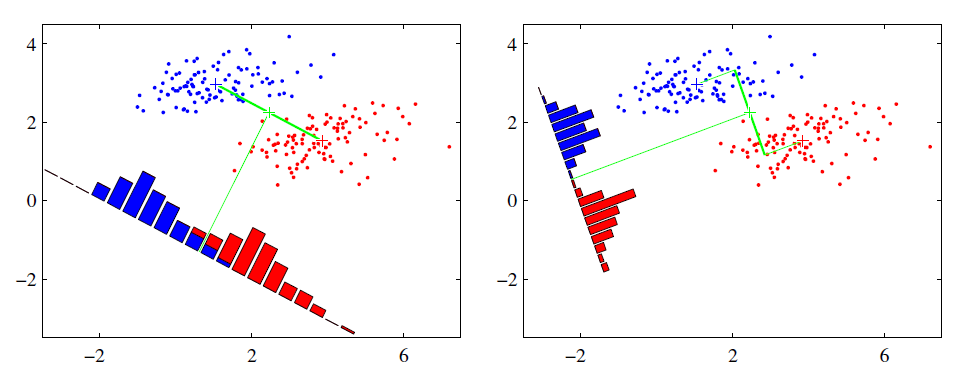
为了使两个样本能够较好的分开，应该是的每一个同类的样本的方差（离散程度）尽可能的小，而不同类的样本的尽可能的远

设样本可以分为$w_1$与$w_2$两类

则我们可以计算

各类样本的类内均值向量
$$\begin{gathered} m_i=\frac{1}{N_i}\sum _{x\in w_i}x \\ \overline{m_i}=\frac{1}{N_i}\sum _{y\in w_i}y \end{gathered}$$

各类样本的类内离散度矩阵
$$\begin{gathered} S_i=\sum _{x\in w_i}(x-m_i){(x-m_i)}^T \\ \overline{S_i}=\sum _{y\in w_i}{(y-\overline{m_i})}^2 \end{gathered}$$
总体样本的类内离散度矩阵
$$\begin{gathered} S_w=S_1+S_2 \\ \overline{S_w}=\overline{S_1}+\overline{S_2} \end{gathered}$$
样本的类间离散度矩阵
$$\begin{gathered} S_b=(m_1-m_2){(m_1-m_2)}^T \\ \overline{S_b}=(\overline{m_1}-\overline{m_2}){(\overline{m_1}-\overline{m_2})}^T \end{gathered}$$
Fisher准则函数
$$J_F(W)=\frac{{(\overline{m_1}-\overline{m_2})}^2}{\overline{S_1}+\overline{S_2}}$$
由此我们优化的目标时使得$J_F(W)$最大
$$\begin{array}{rl}{(\overline{m_1}-\overline{m_2})}^2& =W(m_1-m_2)(m_1-m_2{)}^T{W}^T\\ & =W{S}_b{W}^T\end{array}$$

$$\begin{array}{rl}\overline{S_i}& =\sum _{y\in w_i}{(y-\overline{m_i})}^2\\ & =\sum _{x\in w_i}(Wx-W{m}_i{)}^2\\ & =\sum _{x\in w_i}W(x-m_i)(x-m_i)W^T\\ & =W{S}_i{W}^T\end{array}$$

$$\begin{array}{rl}{J}_F(W)& =\frac{{(\overline{m_1}-\overline{m_2})}^2}{\overline{S_1}+\overline{S_2}}\\ & =\frac{W{S}_b{W}^T}{W(S_1+S_2)W^T}\\ & =\frac{W{S}_b{W}^T}{W{S}_w{W}^T}\end{array}$$

采用拉格朗日乘数法
$$L(W,\lambda )=W{S}_b{W}^T-\lambda (W{S}_w{W}^T-c)$$
对$W$求偏导数
$$\begin{array}{r}\frac{\partial L(W,\lambda )}{\partial W}=S_{b}W-\lambda S_{w}W\end{array}$$
偏导数为0
$$\begin{array}{r}\frac{\partial L(W,\lambda )}{\partial W}=S_{b}W-\lambda S_{w}W=0\end{array}$$
则存在
$$S_{b}W=\lambda S_{w}W$$
因为$S_w$为非奇异矩阵可得到
$$S_w^{-1}{S}_{b}W=\lambda W$$
可以视为求矩阵$S_w^{-1}{S}_b$的特征向量
$$S_w^{-1}{S}_{b}W=S_w^{-1}(m_1-m_2)(m_1-m_2{)}^{T}W$$
$(m_1-m_2{)}^{T}W$为一个标量设为R，则
$$\lambda W=S_w^{-1}(m_1-m_2)R$$
于是
$$W=\frac{R}{\lambda }{S}_w^{-1}(m_1-m_2)$$
由于寻找对是W的方向上的向量，所以
$$W^{\ast }=S_w^{-1}(m_1-m_2)$$
综上所述，存在$W^{\ast }$使得LDA可以较好的解决二分类问题。