1.题目链接：快乐数

2.题目描述：

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：

输入：n = 2
输出：false

提示：

• 1 <= n <= 231 - 1

3.题目分析：

为了⽅便叙述，将「对于⼀个正整数，每⼀次将该数替换为它每个位置上的数字的平⽅和」这⼀个
操作记为x操作；
题⽬告诉我们，当我们不断重复x操作的时候，计算⼀定会「死循环」，死的⽅式有两种：
情况⼀：⼀直在1中死循环，即1 -> 1 -> 1 -> 1…
情况⼆：在历史的数据中死循环，但始终变不到1
由于上述两种情况只会出现⼀种，因此，只要我们能确定循环是在「情况⼀」中进⾏，还是在「情
况⼆」中进⾏，就能得到结果。

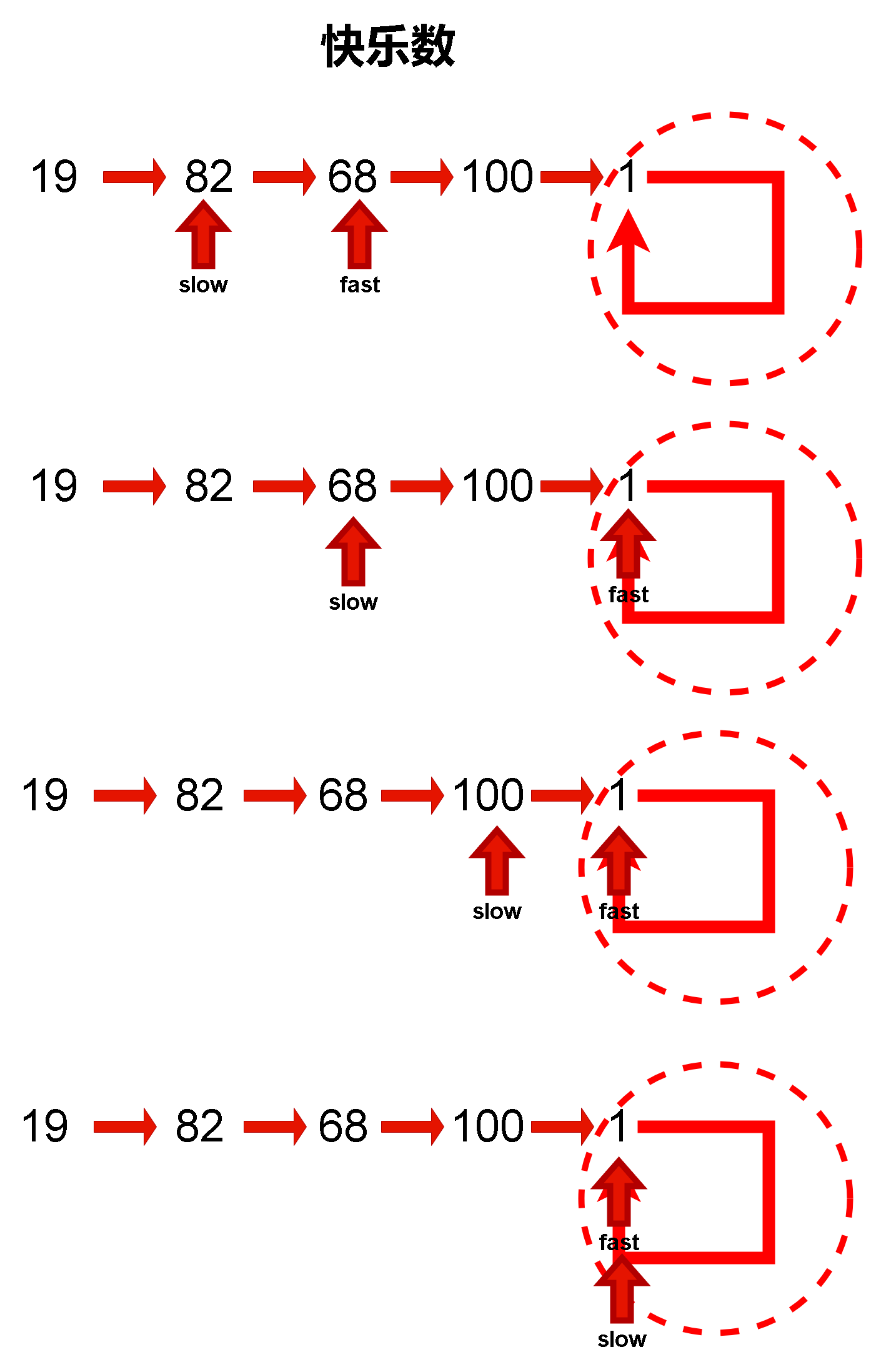
4.算法思路：

但重复执行x的时候，数据会陷入到一个死循环中，利用快慢指针的特性，快指针和慢指针早晚会相遇。如果相遇位置是1，那么这个数一定是快乐数；如果相遇位置不是1，那么就不是快乐数

5.算法流程图：

5.1快乐数流程图：

5.2非快乐数流程图：

6.C++算法代码：

class Solution {
public:
    //返回n这个数每一位上的平方和
    int Sum(int n)
    {
        //求和
        int sum=0;
        while(n)
        {
             //提取个位
            int t=n%10;
            //计算平方和
            sum+=t*t;
            //干掉个位
            n=n/10;
        }
        return sum;
    }
    bool isHappy(int n) {
        //slow指向n的平方，fast指向n的平方的平方
        int slow=Sum(n),fast=Sum(Sum(n));
        while(slow!=fast)
        {
            slow=Sum(slow);
            fast=Sum(Sum(fast));
        }
        return slow==1;
    }
    
};