【模板】二分图最大匹配

题目描述

给定一个二分图，其左部点的个数为 $n$，右部点的个数为 $m$，边数为 $e$，求其最大匹配的边数。

左部点从 $1$ 至 $n$ 编号，右部点从 $1$ 至 $m$ 编号。

输入格式

输入的第一行是三个整数，分别代表 $n$，$m$ 和 $e$。

接下来 $e$ 行，每行两个整数 $u,v$，表示存在一条连接左部点 $u$ 和右部点 $v$ 的边。

输出格式

输出一行一个整数，代表二分图最大匹配的边数。

样例 #1

样例输入 #1

1 1 1
1 1

样例输出 #1

1

样例 #2

样例输入 #2

4 2 7
3 1
1 2
3 2
1 1
4 2
4 1
1 1

样例输出 #2

2

提示

数据规模与约定

对于全部的测试点，保证：

• $1\le n,m\le 500$。
• $1\le e\le 5\times 10^4$。
• $1\le u\le n$，$1\le v\le m$。

不保证给出的图没有重边。

分析

1. 此题就是匈牙利算法的板题，用于求一个二分图的最大匹配数；
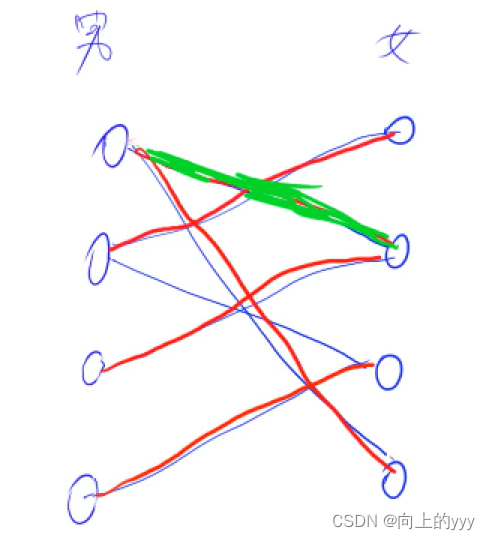
2. 匈牙利算法的过程就是：枚举左部的所有点，对于左部的每一个点，去枚举它的邻边v，判断v是否已匹配（女生已心有所属），如果没有匹配，或者说女生的现男友可以换个对象（实际就是个递归的过程，dfs他的现男友，看看能否换一个女朋友），那么这个女生v就可以和这个男生u匹配，return true；

#include <bits/stdc++.h>

using namespace std;

const int N = 510, M = 50010;
int h[N], e[M], ne[M], idx;
int n, m, edge;
int vis[N];
int match[N];//右边的点所对应的点，也就是右边的妹子现在和谁在一块

void add(int a, int b) {
    e[++idx] = b, ne[idx] = h[a], h[a] = idx;
}

bool dfs(int u) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (!vis[v]) {//这个v（女生）之前没判断过
            vis[v] = 1;
            //如果这个妹子没有匹配到男生 或者 可以让匹配的男生match[v]去找下家
            if (match[v] == 0 || dfs(match[v])) {
                match[v] = u;
                return true;
            }
        }
    }
    return false;
}

int main() {
    cin >> n >> m >> edge;
    memset(h, -1, sizeof h);
    for (int i = 0; i < edge; ++i) {
        int a, b;
        cin >> a >> b;
        add(a, b);
    }
    int ans = 0;
    for (int i = 1; i <= n; ++i) {
        memset(vis, 0, sizeof vis);
        if (dfs(i))
            ans++;
    }
    cout << ans;
    return 0;
}