目录
题目详细:编辑
题目思路:
暴力:
代码详解:
哈希:
二分:
题目详细: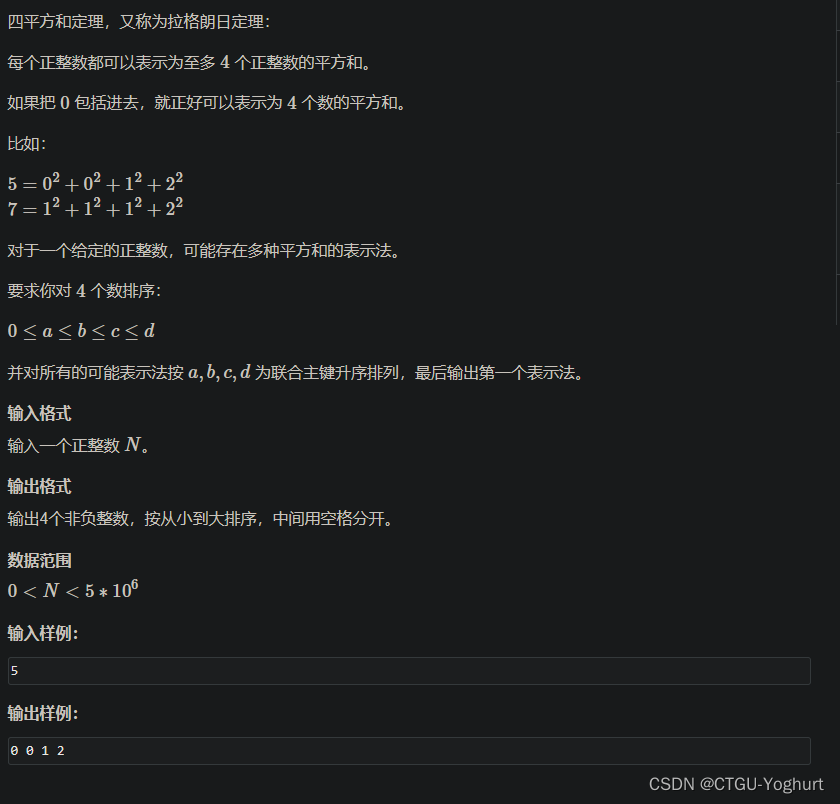
题目思路:
这个题目大家可能马上就可以想到暴力做
例如这样
暴力:
#include<iostream>
#include<cmath>
using namespace std;
int main(){
int n;
cin>>n;
int t=sqrt(n)+1;
for(int a=0;a<=t;a++)
for(int b=a;a*a+b*b<=n;b++)
for(int c=b;a*a+b*b+c*c<=n;c++){
int d=n-a*a-b*b-c*c;
int qd=sqrt(d);
if(qd*qd==d){
printf("%d %d %d %d",a,b,c,qd);
return 0;
}
}
return 0;
}
这样写的话
在题目不卡你数据的时候
可以通过题目
大部分的样例
但仍然不是很好的写法
(浅提一句:在比赛时如果时间不够就可以采用这种写法,以取得更高分数为目标)
那我们要怎么做这道题呢?
首先题目要求的是四个数的平方和
我们枚举每一个数的话一定会太慢
那么我就可以通过枚举两个数
先枚举c和d的所有情况并记录下来
然后再枚举a和b的所有情况
在枚举a和b的所有情况的时候
我们就可以在记录下来的c和d
里面去找是否存在满足条件
使 n=a^2+b^2+c^2+d^2
如果找到则就是正确答案
(注:因为枚举a和b的时候为按照顺序去找,所以我们一旦找到满足条件的a、b、c、d那么他就是最小的abcd字典序)
代码详解:
哈希:
#include<iostream>
#include<cmath>
using namespace std;
const int N=5e6+6;
struct node{
int v,c,d;
}mp[N];
int main(){
int n;
cin>>n;
for(int c=0;c*c<=n;c++)
for(int d=c;c*c+d*d<=n;d++){
int t=n-(c*c+d*d);
if(!mp[t].v) {
mp[t].v=1;
mp[t].c=c;
mp[t].d=d;
}
}
for(int a=0;a*a<=n;a++)
for(int b=a;a*a+b*b<=n;b++){
int t =a*a+b*b;
if(mp[t].v) {
printf("%d %d %d %d",a,b,mp[t].c,mp[t].d);
return 0;
}
}
return 0;
}
二分:
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=5e6+6;
struct node{
int v,c,d;
bool operator<(const node&t) const {
if(v!=t.v) return v<t.v;
if(c!=t.c) return c<t.c;
return d<t.d;
}
}mp[N];
int main(){
int n;
cin>>n;
int pos=0;
for(int c=0;c*c<=n;c++)
for(int d=c;c*c+d*d<=n;d++)
mp[pos++]={n-c*c-d*d,c,d};
sort(mp,mp+pos);
for(int a=0;a*a<=n;a++)
for(int b=a;a*a+b*b<=n;b++){
int t =a*a+b*b;
int l=0,r=pos-1;
while(l<r){
int mid=l+r>>1;
if(mp[mid].v>=t) r=mid;
else l=mid+1;
}
if(mp[l].v==t) {
printf("%d %d %d %d",a,b,mp[l].c,mp[l].d);
return 0;
}
}
return 0;
}
PS:如果采用二分的写法,那么对于记录下来的c和d,需要进行排序。另外对于为什么用从c、d种选择出来的数一定满足从 a<=b<=c<=d 的原因就比如(a=1,b=2,c=0,d=0)我们一定可以先找到(a=0,b=0,c=1,d=2)满足题目要求的答案,故为最正解。
PPS:寒假摆烂玩宝可梦真好