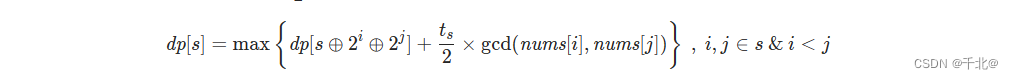一、问题描述

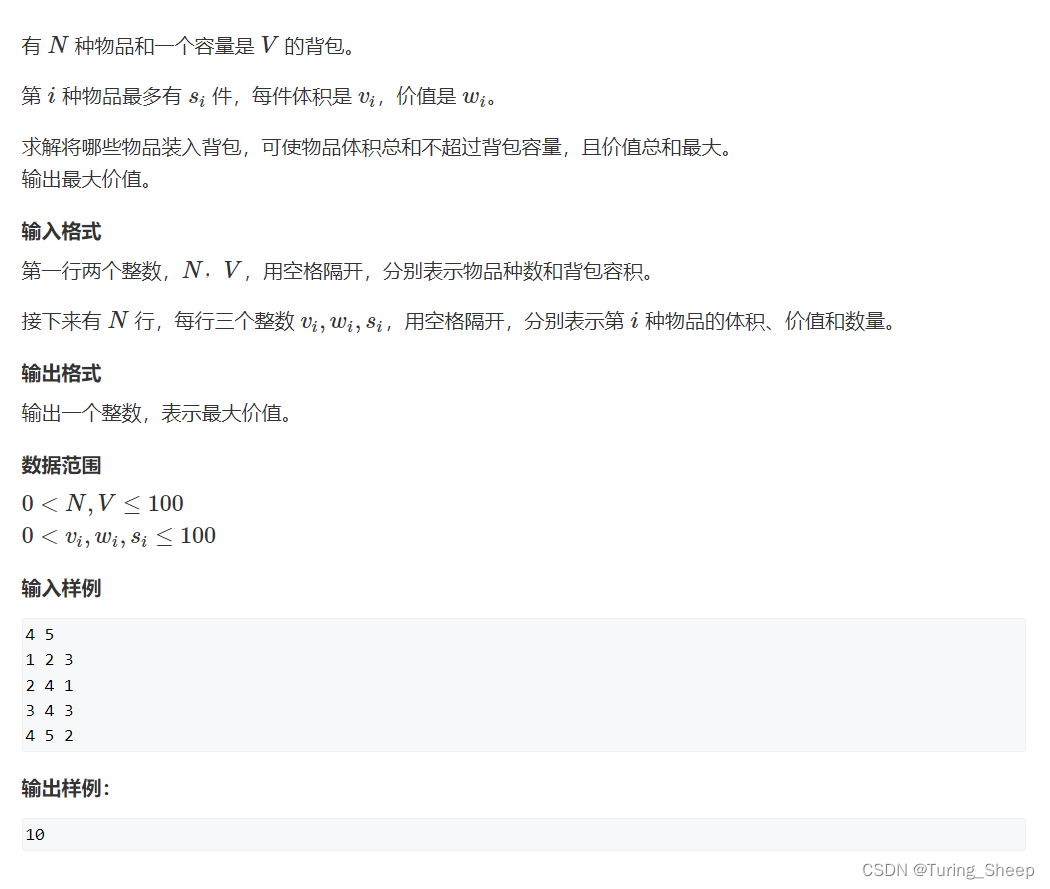
二、思路分析

这道题同样是背包问题，那么它也同样满足三个性质：重叠子问题、最优子结构以及无后效性。那么这样的话，我们依然可以使用动态规划的思路去分析这道题目。那么动态规划的分析主要分为两步：状态转移方程的书写以及循环的设计。

1、状态转移方程

（1）状态表示：

我们在前面的两篇文章中介绍过，对于背包问题而言，我们一般用一个二维数组来表示dp数组，即我们经常写的：$f(i,j)$

那么$f(i,j)$的意思是，当物品数量为$i$，自己的背包容量是$j$的时候，我们所能携带的最大价值：$f[i][j]$。

（2）状态转移：

状态转移的目的是为了能够将大规模的问题转化成较小规模的问题。

背包问题中，状态转移方程的书写就一个技巧：活在当下

我们此时共用$i$个物品，我们不可能一下子就同时做出多个决策，从而得到最优解。我们就看眼前，我们眼前的就是第$i$个物品，而我们要做的决策就是，第$i$个物品到底选不选，选的话，在背包容量允许的条件下，我们选几个？

如果我们不选的话，我们就能写出下列的方程：

$$f(i,j)=f(i-1,j)$$

由于我们不选第$i$个物品，所以我们只需要考虑前$i-1$个。这样我们就把规模从$i$降低到了$i-1$。

假设我们选的话，那么就能够写成下列形式：（$v[i]$表示第$i$个物品的体积，$w[i]$表示第$i$个物品的价值）

$$f(i,j)=f(i-1,j-v[i]\ast k)+w[i]\ast k$$

上述等式成立的前提是保证：$j\ge v[i]\ast k$

我们只需要在上述的这些情况中取一个最大值即可：

所以我们的状态转移方程可以表示为：

$$f(i,j)=max\{\begin{array}{ll}f(i-1,j)& \\ f(i-1,j-v[i])+w[i]& j\ge v[i]\\ f(i-1,j-v[i]\ast 2)+w[i]\ast 2& j\ge v[i]\ast 2\\ ......& \\ f(i-1,j-v[i]\ast k)+w[i]\ast k& j\ge v[i]\ast k\end{array}$$

2、循环设计

我们的循环和之前所介绍的01背包问题、完全背包问题的循环设计是一样的，最外层循环是背包的规模从小到大，第二层的循环是背包的容量，从小到大。

三、代码模板

1、朴素版

我们综合上面的思路，就能够写出下面的代码：

#include<iostream>
using namespace std;
const int N=110;
int f[N][N],v[N],w[N],q[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d",v+i,w+i,q+i);
    }
    for(int i=1;i<=n;i++)//枚举物品规模
    {
        for(int j=0;j<=m;j++)//枚举背包容量
        {
            for(int k=0;k*v[i]<=j&&k<=q[i];k++)//书写状态转移方程
            {
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

2、优化版

我们发现上面的这个朴素版代码包含了三重循环，那么我们如何降低一层循环呢？

其实，我们的多重背包可以转化成01背包问题。这样讲肯定很抽象，大家可以看下面的图：

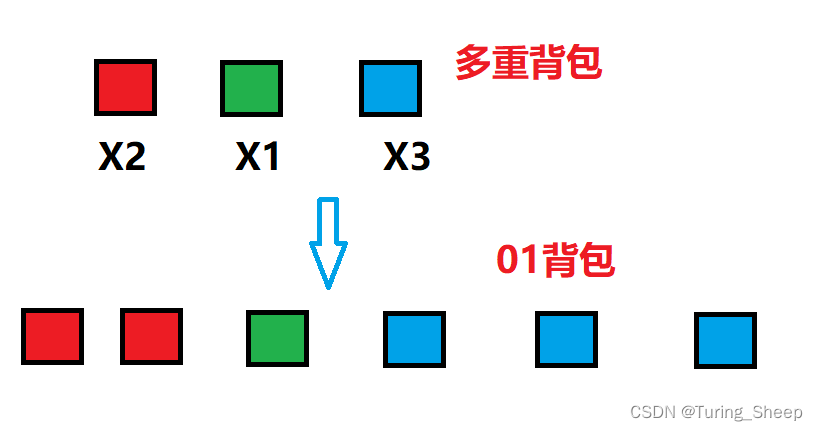
但是这样做的话只是形式上做了优化，从$n^3$到$n^2$，但实际上依旧是一个$n^3$的时间复杂度。

而这样没有成功优化的原因是因为我们有$n$个$i$物品，就需要重复$n$个i物品。那么我们是否存在一种方式，我们不需要枚举$n$次i物品，就能够表示$n$个$i$物品呢？

答案是有的。

我们的十进制数可以用二进制数来表示。

假设我们的二进制位有4位：

那么我们能表示的范围是：$0000$ ~ $1111$。

而

$1111=1000+0100+0010+0001$

上面右侧的四个部分组成了这个数字。

我们可以从形式上掌握一下，这个四个部分所代表的含义就是对应的位数是1。

$1000$：第四位是1
$0100$：第三位是1
$0010$：第二位是1
$0001$：第一位是1

接着我们发现，$0000$到$1111$之间的任何一个数字，其实无非是某位是0，某位是1。如果某位是1，我们只需要加上上面四个数字中的其中一个。

例如：
$1001=1000+0001$
$1101=1000+0001+0100$

因此我们就能够得到一个结论，我们能够有这四个数字表示$0000$到$1111$之间的所有数字。

转换成十进制而言，就是说我们能够用$1$,$2$,$4$,$8$表示出$0$到$15$之间的任何数字。

所以，我们可以利用几个$2^k$，其中$（k=0，1，2，...）$，来表达一个范围内的所有数字。根据我们刚才的推导，所能表示的范围其实就是我们刚刚这几个数加在一起时的值，其实就是一个等比数列求和。

用数学公式表达就是

我们可以利用：$2^0、2^1、2^2、2^3、...、2^k$表示$0$ ~ 2^(k+1)$-1$之间的所有数字。

那么如果我们的要表达的200

那么我们可以利用：
$2^0、2^1、2^2、2^3、2^4、2^5、2^6$

这几个数能表达的最大值是：$2^7-1=127$

那么从128到200怎么表示呢？

其实我们只需要多加一个73即可。

也就是说，我们可以用：

$2^0、2^1、2^2、2^3、2^4、2^5、2^6、73$
来表达0-200。

为什么呢？

我们只用前面的这些$2^k$。那么我们能表示的是$0-127$。
如果我们每次选择的时候都加上一个73，我们能表示的范围就是：
$73-200$

虽然两部分之间有一点重叠的部分，但是重叠的话，无非就是我们重复计算了几个相同情况而已，并不影响我们结果的正确性。

那么我们发现，此时我们利用$O(logn)$级别的数字表示了$O(n)$。

时间上做了非常大的优化。

而这种优化方式被称作二进制优化。

如图所示：

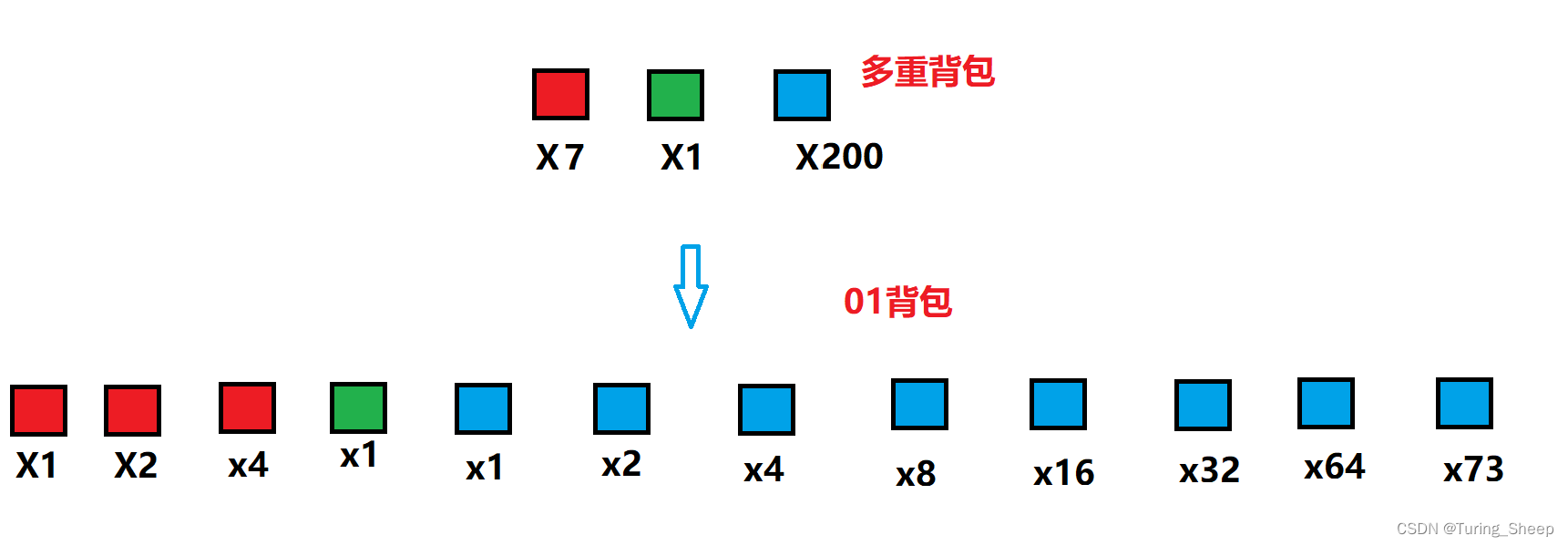
根据上面的思路，我们就能够写出下面的优化版本的代码：

#include<iostream>
using namespace std;
const int N=3e4+10;
int dp[N],v[N],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    int cnt=1;
    for(int i=1;i<=n;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        int k=1;
        //进行 “打包” 转换：二进制优化，转换成01背包
        while(k<c)
        {
            v[cnt]=k*a,w[cnt++]=k*b;
            c-=k;
            k*=2;
        }
        if(c>0)
            v[cnt]=c*a,w[cnt++]=c*b;
    }
    //利用01背包中的空间优化模板求解。
    for(int i=1;i<=cnt;i++)
        for(int j=m;j>=v[i];j--)
                dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
    cout<<dp[m]<<endl;
    return 0;
}