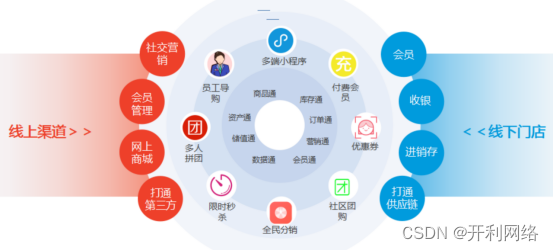
身处今数字化时代,建立线上线下相结合的数字化新零售体系是企业成功的关键。蚓链数字化营销系统致力于帮助企业实现数字化转型,打通线上线下销售渠道,提升品牌影响力和用户黏性,那么具体是如何建立的?
1. 搭建数字化中台。基于中台系统将企业的产品、库存、价格、营销等各个方面的数据集成在一起,实现数据的共享和统一管理。通过数字化中台,企业可以更好地了解客户的需求和行为,更精准地制定营销策略。
2. 整合数字化前台。这个前台包括企业的官方网站、社交媒体账号、小程序、APP等多种数字化渠道,可以吸引更多的目标客户,提高用户体验和品牌认知度。蚓链数字化营销系统具备上述多端开发能力,可以通过数字化前台,实现个性化的推荐和营销,提高销售业绩和用户满意度。
建立线上线下相结合的数字化新零售体系需要企业全面考虑数字化转型的各个环节,将线上和线下的销售渠道打通,提高销售效率,满足消费者的需求。同时,企业也需要建立线上的会员体系和积分系统,与用户建立更紧密的联系,提高用户的忠诚度和复购率。通过注重数据的集成和共享、制定个性化的营销策略、实现O2O的销售模式等多种手段,才能够更好地满足消费者的需求,提高企业的业务成果和持续发展能力。