线性代数 --- 矩阵的QR分解，A=QR

news2024/9/22 7:35:58

矩阵的QR分解，格拉姆施密特过程的矩阵表示

首先先简单的回顾一下Gram-Schmidt正交化过程的核心思想，如何把一组线性无关的向量构造成一组标准正交向量，即，如何把矩阵A变成矩阵Q的过程。

给定一组线性无关的向量a,b,c，我们希望构造出一组相互垂直的单位向量。

$A=\begin{bmatrix} | & |& |\\ a& b&c \\ | & |& | \end{bmatrix}$

第一步：

$\mathbf{A=a}$

得到一组正交向量中的第一个向量A，这就是说，我们令新的正交向量中的第一个向量A与向量a的方向相同，且大小相同。（这里我们用到了向量a）

第二步：

$\mathbf{B=b-\frac{A^{T}b}{A^{T}A}A}$

A的已经确定了，第二个向量B必须垂直于A。我们令b减去b在A上的投影Pb，得到我们想要的第二个向量B。a,b与A,B不同，但都在同一个平面内。注意：向量B一定不等于0，否则的话就与a,b线性无关这一事实相左。(这里我们用到了向量b)

第三步：

$\mathbf{C=c-\frac{A^{T}c}{A^{T}A}A-\frac{B^{T}c}{B^{T}B}B}$

现在我们基于c去找第三个向量C，C必须垂直于A,B所张成的平面，即A,B所在的子空间。我们令c减去c在这个平面上的投影Pc,得到向量C。

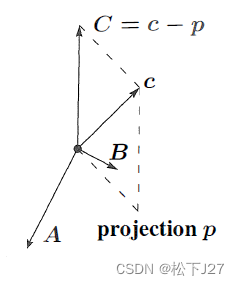
如果还有第四个，第五个向量d,e,f,g......的话，我们只需把在这个基础上重复上述过程就能找到新的正交向量D,E,F,G......。

第四步：

$\mathbf{q_{1}=\frac{A}{\left \| A \right \|},q_{2}=\frac{B}{\left \| B \right \|},q_{3}=\frac{C}{\left \| C \right \|}}$

当我们把前面的正交向量A,B,C全部找完以后，让他们分别除以各自的长度，最终得到一组标准正交向量q1,q2,q3。这最后一步被称为向量的归一化。

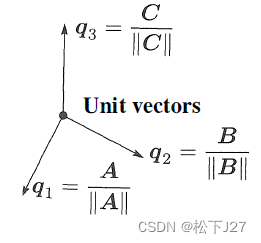
例：

已知一组线性无关的向量a,b,c：

$a=\begin{bmatrix} 1\\ -1\\ 0 \end{bmatrix} \; b=\begin{bmatrix} 2\\ 0\\ -2\end{bmatrix} \; b=\begin{bmatrix} 3\\ -3\\ 3 \end{bmatrix}$

第一步：令A=a得到

$A=\begin{bmatrix} 1\\ -1\\ 0 \end{bmatrix}$

第二步：从b中减去b在A上的投影得到

$B=b-\frac{A^{T}b}{A^{T}A}A=b-\frac{2}{2}A=\begin{bmatrix} 1\\ 1\\ -2 \end{bmatrix}$

第三步：从c中减去c在AB平面上的投影得到

$C=c-\frac{A^{T}c}{A^{T}A}A-\frac{B^{T}c}{B^{T}B}B=c-\frac{6}{2}A+\frac{6}{6}B=\begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix}$

第四步：归一化

$\left \| A \right \|=\sqrt{A^{T}A}=\sqrt{2}, \; \left \| B \right \|=\sqrt{B^{T}B}=\sqrt{6}, \; \left \| C \right \|=\sqrt{C^{T}C}=\sqrt{3}$

$q_{1}=\frac{A}{\left \| A \right \|}=\frac{1}{\sqrt{2}}\begin{bmatrix} 1\\ -1\\ 0 \end{bmatrix}\; q_{2}=\frac{B}{\left \| B \right \|}=\frac{1}{\sqrt{6}}\begin{bmatrix} 1\\ 1\\ -2 \end{bmatrix}\; q_{3}=\frac{C}{\left \| C \right \|}=\frac{1}{\sqrt{3}}\begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix}\;$