题目描述

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

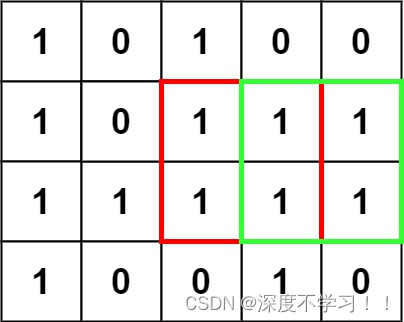
输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：4

思路分析

看了一圈题解，解释的都不太清楚。我来写一个。

这题动规。直接步骤开走。

1.确定dp下标含义：

dp[i][j] 表示为 以i和j为右下角的格子可以组成的正方形的最长边长。

2.递推公式：

dp[i][j]=min(dp[i−1][j−1],dp[i−1][j],dp[i][j−1])+1。
含义为若当前位置为111，则此处可以构成的最大正方形的边长，是其正上方，左侧，和左上界三者共同约束的，且为三者中的最小值加1。

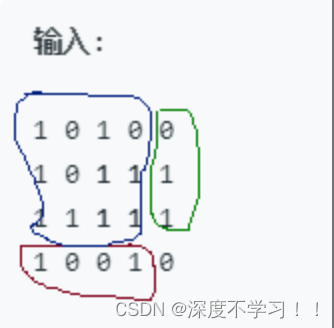
看下面这个图帮助理解，假设当前 i j 遍历到最右下角的0的时候，则此时dp[i][j]也就是算上当前这个格子，可以组成的最长边长，即由图中红蓝绿三个矩形来决定的。
也就是说，这三部分联合到一起，再加上当前遍历的右下角这一个小格子，才算是一个新的正方形，这也是为什么要取三者中的min值了，这也意味着，只有三个条件相等，边长才能变大。

3.初始化：

初始化比较容易，为了考虑一个格子的情况，也就是所给的matrix 数组第一行和第一列的元素，将dp数组进行扩充，扩充一行一列，这样就能清楚的表示所给矩阵第一行和第一列正方形的情况了。

完整代码

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        # dp[i][j] 为 以i和j为右下角的格子可以组成的正方形的最长
        row = len(matrix)+1
        col = len(matrix[0])+1
        res = 0

        dp = [[0 for _ in range(col)] for _ in range(row)]
        

        for i in range(1,row):
            for j in range(1,col):
                if matrix[i-1][j-1] == '1':
                    dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1
                res = max(res,dp[i][j])
        return res * res
        ```