常用排序算法详解

1.冒泡排序
- 原理
- 示例
- 代码实现
2.快速排序
- 原理
- 示例
- 代码实现
3.插入排序
- 原理
- 示例
- 代码实现
4.希尔排序
- 原理
- 示例
- 代码实现
5.选择排序
- 原理
- 示例
- 代码实现
6.堆排序
- 原理
- 示例
- 代码实现
7.归并排序
- 原理
- 示例
- 代码实现

本文讲述了常见的排序算法的执行过程，有详细实现过程举例

1.冒泡排序

原理

冒泡排序是指不断的遍历数组，比较相邻两个数的大小，如果顺序不对就将其掉换位置，直到所有的数据位置都正确

示例

原始数组：[ 6 , 1 , 8 , 3 , 5 , 9 , 2 , 4 ]

操作次数	排序结果	操作
原始数组	[`6,1`, 8 , 3 , 5 , 8 , 2 , 4 ]	进行第一次遍历，比较6和1，位置不对交换
第一次交换结果	[ 6 ,`1, 8`, 3 , 5 , 9 , 2 , 4 ]	比较1和8，不交换
第二次交换结果	[ 6 , 1 ,`8,3`, 5 , 9 , 2 , 4 ]	比较8和3，交换
第三次交换结果	[ 6 , 1 , 3 ,`8,5`, 9 , 2 , 4 ]	比较8和5，交换
第四次交换结果	[ 6 , 1 , 3 , 5 ,`8,9`, 2 , 4 ]	比较8和9，不交换
第五次交换结果	[ 6 , 1 , 3 , 5 , 8 ,`9,2`, 4 ]	比较9和2，交换
第六次交换结果	[ 6 , 1 , 3 , 5 , 8 , 2 ,`9,4`]	比较9和4，交换
第七次交换结果	[ 6 , 1 , 3 , 5 , 8 , 2 , 4 ,`9`]	第一次有交换，遍历第二次
遍历第二次结果	[ 1 , 3 , 5 , 6 , 2 , 4 ,`8,9`]	第二次有交换，遍历第三次
遍历第三次结果	[ 1 , 3 , 5 , 2 , 4 , `6,8,9`]	第三次有交换，遍历第四次
遍历第四次结果	[ 1 , 3 , 2 , 4 , `5,6,8,9`]	第四次有交换，遍历第五次
遍历第五次结果	[ 1 , 2 , 3 , `4,5,6,8,9`]	第五次有交换，遍历第六次
遍历第六次结果	[`1,2,3,4,5,6,8,9`]	第六次无交换，遍历结束

代码实现

    public static int[] sort(int[] sourceArray) throws Exception {
        //冒泡排序
        int length = sourceArray.length;//获取数组长度
        int[] arr = sourceArray;//拷贝数组
        //for循环用于进行书组遍历
        for (int i = 0; i < length ; i++) {
            int l = 0,r = 1;//定义左右指针
            int a = 0;//用于记录交换次数
            //while循环用于每次遍历下的数据交换
            while (l<length && r<length){
                if (arr[l] < arr[r] ) {
                    //左小于右（正确顺序）针指i和j整体向右挪一个
                    l++;
                    r++;
                }else {
                    //左大于右（不正确顺序）交换左右，然后针指i和j整体向右挪一个
                    //交换左右
                    int t = arr[l];
                    arr[l] = arr[r];
                    arr[r] = t;
                    //然后针指i和j整体向右挪一个
                    l++;
                    r++;
                    //记录交换次数
                    a++;
                }
            }
            //判断此次遍历是否发生数据交换
            if (a == 0){
                break;
            }
        }
        //返回排序后的结果
        return arr;
    }

2.快速排序

原理

1.先从数列中取出一个数作为key值（标杆值）；
2.将比这个数小的数全部放在它的左边，大于或等于它的数全部放在它的右边；

挖坑填数字，每次比较都拿出一个标杆来和数据进行比较，先从右往左比，遇到比标杆小的就将其放在标杆的坑里（标杆数字所在的数组位置），换过去的数字所在位置成为新的坑，然后在从原来标杆的那个坑（刚刚放进数字的位置）从左往右比较，遇到比标杆数字大或等于的，就放在此时标杆位置所在的坑中，然后再从现在的这个刚放进去数字的坑从有往左比较，知道所有数字均符合左边比标杆小，右边比标杆大

3.对左右两个小数列重复第二步，直至各区间只有1个数。

示例

原始数组：[ 6 , 1 , 8 , 3 , 5 , 9 , 2 , 4 ]
对原始数组进行第一个标杆的比较：

操作	标杆数据	结果	下一步比较
拿出标杆数据	6	[ `_`, 1 , 8 , 3 , 5 , 9 , 2 , 4 ]	<从右往左比，比较4和标杆数据
4小于标杆数据，4填坑	6	[`4`, 1 , 8 , 3 , 5 , 9 , 2 , `_` ]	>从左往右比，比较1和标杆数据
1小于标杆数据，不变	6	[4, `1` , 8 , 3 , 5 , 9 , 2 , `_` ]	>从左往右比，比较8和标杆数据
8大于标杆数据，8填坑	6	[4, 1 , `_`, 3 , 5 , 9 , 2 , `8` ]	<从右往左比，比较2和标杆数据
2大于标杆数据，2填坑	6	[4, 1 , `2`, 3 , 5 , 9 ,`_`, 8 ]	>从左往右比，比较3和标杆数据
3小于标杆数据，不变	6	[4, 1 , 2,`3` , 5 , 9 ,`_`, 8 ]	>从左往右比，比较5和标杆数据
5小于标杆数据，不变	6	[4, 1 , 2, 3 , `5` , 9 ,`_`, 8 ]	>从左往右比，比较9和标杆数据
9大于标杆数据，9填坑	6	[4, 1 , 2, 3 , `5` ,`_` ,9, 8 ]	左右比较交汇，该标杆放回坑内
标杆放回坑里		[4, 1 , 2, 3 , 5 ,`6` ,9, 8 ]	该轮比较结束，对标杆6左右进行上述比较

对标杆两边重复上述操作：
（1）标杆6左边数据比较：得到：[ 1,2,3,4,5 ]

操作	标杆数据	结果	下一步比较
拿出标杆数据	4	[ `_` , 1 , 2, 3 , 5 ]	<从右往左比，比较5和标杆数据
5大于标杆数据，不变	4	[ `_` , 1 , 2, 3 , `5` ]	<从右往左比，比较3和标杆数据
3小于标杆数据，3填坑	4	[`3`, 1 , 2, `_` , 5 ]	>从左往右比，比较1和标杆数据
1小于标杆数据，不变	4	[3, 1 , 2, `_` , 5 ]	>从左往右比，比较2和标杆数据
2小于标杆数据，不变	4	[3, 1 , `2`, `_` , 5 ]	左右比较交汇，该标杆放回坑内
标杆放回坑里，对左右比较		[3, 1 , 2, `4` , 5 ]	该轮比较结束,对标杆4左右比较，右边只有一位不比较
标杆4左边比较	3	[2, 1 ,`3` ]	该轮比较结束,对标杆3左右比较，右边没有不比较
对标杆3左右比较	2	[ 1, `2` ]	该轮比较结束，标杆左边只有一位，不再比较

（2）标杆6右边数据比较：得到：[ 8,9 ]

操作	标杆数据	结果	下一步比较
拿出标杆数据	9	[ `_`, 8 ] <从右往左比，比较8和标杆数据
2小于标杆数据,8填坑	9	[ `8`, `_` ] 左右比较交汇，该标杆放回坑内
标杆放回坑里		[ 8, `9` ]	该轮比较结束，标杆左边只有一位，不再比较

最终的到数据：[ 1,2,3,4,5,6,8,9 ]

代码实现

public static void quickSort(int a[],int l,int r){
     if(l>=r)
       return;

     int i = l; int j = r; int key = a[l];//选择第一个数为标杆

     while(i<j){

         while(i<j && a[j]>=key)//从右向左找第一个小于标杆的值
             j--;
         if(i<j){
             a[i] = a[j];
             i++;
         }

         while(i<j && a[i]<key)//从左向右找第一个大于标杆的值
             i++;

         if(i<j){
             a[j] = a[i];
             j--;
         }
     }
     //i == j
     a[i] = key;
     quickSort(a, l, i-1);//递归调用
     quickSort(a, i+1, r);//递归调用
 }

3.插入排序

原理

1.将数组第一个数当成一个有序数组，然后从第二个数据开始看作无序数组
2.每次拿出无序数组中的第一个数据和有序数组的最后一位开始向前比较
3.将拿出的数据插入有序数组中的合适位置
4.重复上述步骤直至无序数组中所有的数据全部插入有序数组中。

示例

原始数组：[ 6 , 1 , 8 , 3 , 5 , 9 , 2 , 4 ]

操作	有序数组	无序数组	拿出来的数据
将数组分成有序数组和无序数组	6	`1`、8、3、5、9、2、4	1
`从后往前`比较有序数组，将`1`插入有序数组	`1`、6	`8`、3、5、9、2、4	8
`从后往前`比较有序数组，将`8`插入有序数组	1、6 、`8`	`3`、5、9、2、4	3
`从后往前`比较有序数组，将`3`插入有序数组	1、`3`、6 、8	`5`、9、2、4	5
`从后往前`比较有序数组，将`5`插入有序数组	1、3、`5`、6 、8	`9`、2、4	9
`从后往前`比较有序数组，将`9`插入有序数组	1、3、5、6 、8、`9`	`2`、4	2
`从后往前`比较有序数组，将`2`插入有序数组	1、`2`、3、5、6 、8、9	`4`	4
`从后往前`比较有序数组，将`4`插入有序数组	1、2、3、`4`、5、6 、8、9

代码实现

    public static void main(String[] args) {
        int[] nums={ 6 , 1 , 8 , 3 , 5 , 9 , 2 , 4 };
        int start=1;
        for(start=1;start<nums.length;start++) {
            int insert=nums[start];//将数组第二个数据拿出放入insert，做为待插入的数据
            while(start>0) {
                if(nums[start-1]>insert) {
                //从后往前比较，遇到比该数字大的了就将大的数字往后挪一个位置
                    nums[start]=nums[start-1];
                } else {
                //若遇到和拿出数字相同的数据，则将insert放入当前空缺位置
                    nums[start]=insert;
                    break;//结束当前循环
                }
                start--;//比较的数字往前挪一个
            }
            if(start==0) {
                nums[0]=start;
            }
        }
 
        for (int i = 0; i < nums.length; i++) {
            System.out.print(nums[i]+" ");
        }
    }

4.希尔排序

希尔排序也称递减增量排序，是对插入排序的改进，以牺牲稳定性的方法提高效率。

原理

1.根据数组长度确定增长量k2（k1 = length / 2）（例如：数组[ 1 , 5 , 3 , 8 , 9 , 3 ]）
2.按照增量数列进行分组，一般分成k组（每组数据的两个数据相距k个位置，例如：k为3时，位置0和位置3一组，位置1和位置4一组，位置2和位置5一组）
3.比较每组的数据将其按照增量排序（比较：位置0和位置3数据，位置1和位置4数据，位置2和位置5数据，位置不对的交换）
4.确定增长量k2（k2 = k2 / 2）
5.按照增量数列进行分组，分为k2组（例如：k2 = 2 ，分组：位置0 位置2 位置4一组，位置1 位置3 位置5一组）
6.比较每组的数据将其按照增量排序
…（循环以上步骤直至k=1时为最后一趟）

示例

原始数组：[ 6 , 1 , 8 , 3 , 5 , 9 , 2 , 4 ]

操作	k值	结果
计算k值，将原始数据分为k组	4	6 , 1 , `8` , 3 , 5 , 9 , `2` , 4
四组分别排序(交换了第一组6,5 ，第三组8,2)	4	5 , 1 , `2` , 3 , 6 , 9 , `8` , 4
重新计算k，将数据分为k组	2	5, `1` , 2 , `3` , 6 , `9` , 8 , `4`
两组分别排序	2	2, `1` , 5 , `3` , 6 , `4` , 8 , `9`
计算k，并分组	1	2, 1 , 5 , 3 , 6 , 4 , 8 , 9
排序	1	1, 2 , 3 , 4 , 5 , 6 , 8 , 9

代码实现

    public static void main(String[] args) {
        int[] nums={1,5,7,9,3,2,4,0,6,8,5};
        //控制增量序列,增量序列为1的时候为最后一趟
        for (int i = nums.length/2; i > 0; i/=2) {
            //根据增量序列，找到每组比较序列的最后一个数的位置
            for (int j = i; j <nums.length ; j++) {
                //根据该比较序列的最后一个数的位置，依次向前执行插入排序
                for (int k = j-i; k >= 0 ; k-=i) {
                    if(nums[k]>nums[k+i]) {
                        int tmp=nums[k];
                        nums[k]=nums[k+i];
                        nums[k+i]=tmp;
                    }
                }
            }
        }
        System.out.println(Arrays.toString(nums));
    }

5.选择排序

原理

1.将数组中最小的数据拿出，放在数组第一个作为排序数组
2.在未排序数组中找出最小的，放在拍叙述组的尾部
3.循环执行，直到所有的数字排序完成

示例

原始数组：[ 6 , 1 , 8 , 3 , 5 , 9 , 2 , 4 ]

操作	排序数组	未排序数组	未排序数组中最小的
原始数组		6 , `1` , 8 , 3 , 5 , 9 , 2 , 4	1
将1放在数组第一位最为排序数组	`1`	6 , 8 , 3 , 5 , 9 , `2` , 4	2
将1放在数组第一位最为排序数组	1，`2`	6 , 8 , `3` , 5 , 9 , 4	3
将1放在数组第一位最为排序数组	1，2，`3`	6 , 8 , 5 , 9 , `4`	4
将1放在数组第一位最为排序数组	1 ，2，3，`4`	6 , 8 , `5` , 9	5
将1放在数组第一位最为排序数组	1 ，2，3，4，`5`	`6` , 8 , 9	6
将1放在数组第一位最为排序数组	1，2，3，4，5，`6`	`8` , 9	8
将1放在数组第一位最为排序数组	1，2，3，4，5，6，`8`	`9`	9
将1放在数组第一位最为排序数组	1，2，3，4，5，6，8 ，`9`

代码实现

    public static void main(String[] args) {
        int[] nums={1,5,7,9,3,2,4,0,6,8,5};
        int start=1;
        for(start=1;start<nums.length;start++) {
            int insert=nums[start];
            while(start>0) {
                if(nums[start-1]>insert) {
                    nums[start]=nums[start-1];
                } else {
                    nums[start]=insert;
                    break;
                }
                start--;
            }
            if(start==0) {
                nums[0]=start;
            }
        }
 
        for (int i = 0; i < nums.length; i++) {
            System.out.print(nums[i]+" ");
        }
    }

6.堆排序

堆排序是一种选择排序
堆是一颗完全二叉树：
当所有的结点的值都大于或等于其左右的子结点的值称为大顶堆
当所有的结点的值都小于或等于其左右的子结点的值称为小顶堆

原理

1.先将数组排序成一个大根堆
2.将根节点和最后一个叶子借点交换
3.将非最后一个叶子节点的其他数据排序成大根堆（此时最后一个叶子节点为上一轮排序中的根节点，最大的数据，位置已经确定了）
4.交换该大根堆中的根节点和最后一个叶子结点
…（循环直到所有数据均排列完成）

示例

操作	数组
原始数组	6 , 1 , 8 , 3 , 5 , 9 , 2 , 4
第一轮大根堆交换节点后结果	3，5，8，4，1，6，2，`9`
第二轮大根堆交换节点后结果	2，5，6，4，1，3，`8`，`9`
第三轮大根堆交换节点后结果	2，5，3，4，1，`6`，`8`，`9`
第四轮大根堆交换节点后结果	1，4，3，2，`5`，`6`，`8`，`9`
第五轮大根堆交换节点后结果	1，2，3，`4`，`5`，`6`，`8`，`9`
第六轮大根堆交换节点后结果	1，2，`3`，`4`，`5`，`6`，`8`，`9`
第七轮大根堆交换节点后结果	1，`2`，`3`，`4`，`5`，`6`，`8`，`9`
第八轮大根堆交换节点后结果	`1`，`2`，`3`，`4`，`5`，`6`，`8`，`9`

具体过程：
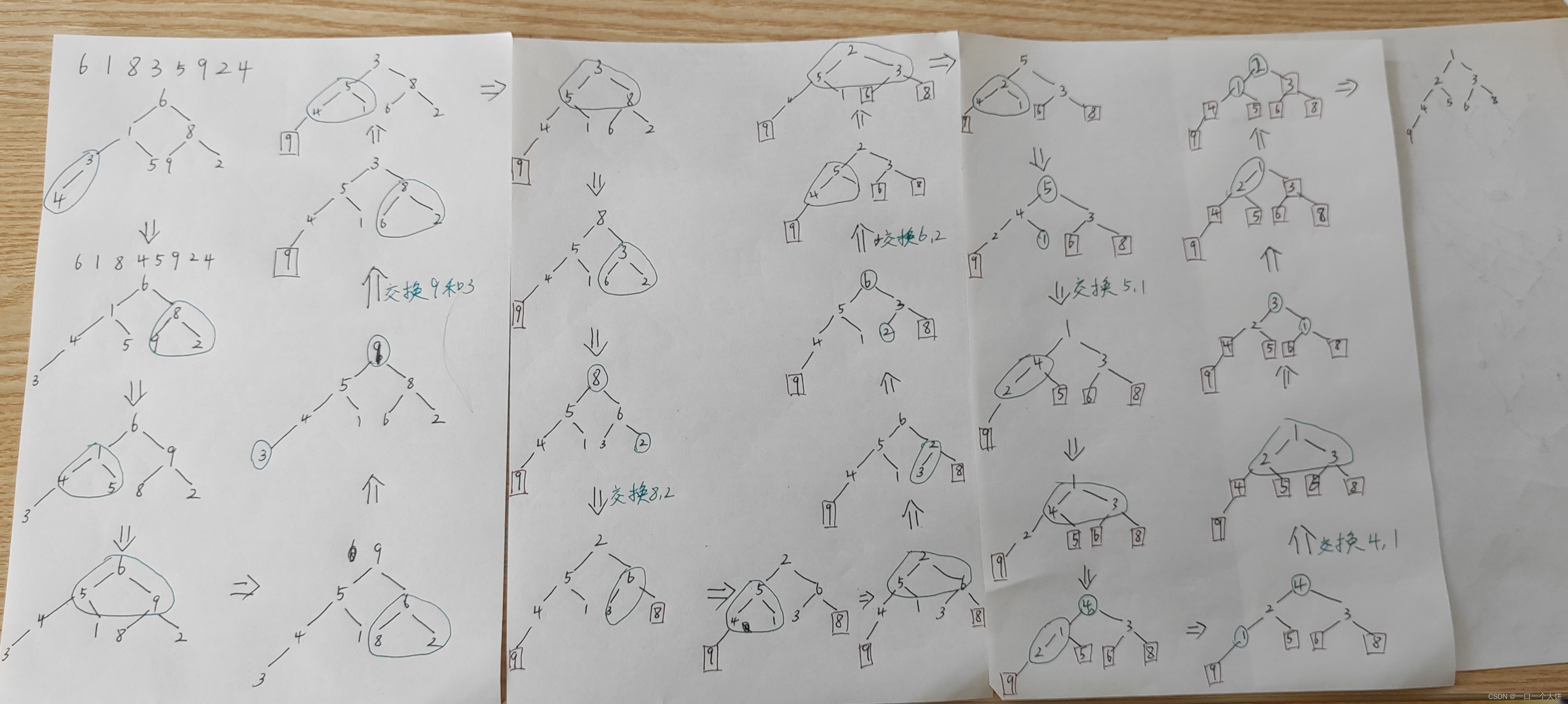
在这里插入图片描述

代码实现

import java.util.Arrays;
 
public class HeapSort {
    public static void main(String[] args) {
        int[] arr = {3, 5, 2, 7,4,5,8,2,1,9,0,5,4};
        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }
 
    //堆排序
    public static void heapSort(int[] arr) {
        //将无序序列构建成一个堆
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            adjustHeap(arr, i, arr.length);
        }
        //将堆顶元素和末尾元素交换,将最大元素放置数组末端
        //重新调整至堆结构,然后继续将堆顶元素和当前末尾元素交换,以此往复
        for (int i = arr.length - 1; i > 0; i--) {
            int temp = arr[i];
            arr[i] = arr[0];
            arr[0] = temp;
            adjustHeap(arr, 0, i);
        }
    }
 
    // 将二叉树调整为堆
     
    public static void adjustHeap(int[] arr, int i, int length) {
        int temp = arr[i];
        //k=2i+1是i的左子结点
        for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
            if (k + 1 < length && arr[k] < arr[k + 1])//左子结点的值<右子结点的值
                k++;//指向右节点
            if (arr[k] > temp) {//如果子结点的值>根节点的值
                arr[i] = arr[k];//将较大的值赋给当前结点
                i = k;//i指向k,继续循环比较
            } else
                break;
        }
        //for循环后,已经将以i为根结点的树的最大值,放在了顶部
        arr[i] = temp;//将temp值放到调整后的位置
    }
}

7.归并排序

原理

1.将数组分成不同的组，每次平均分成两个数组，直到无法分成两份
2.将两个长度为1的数组合并成一个长度为2的有序数组
3.将两个长度为2的数组合并成一个长度为4的有序数组
…(重复多遍)
4.直至和并完成

示例

操作	数组结果
原始数组	[ 6 , 1 , 8 , 3 , 5 , 9 , 2 , 4 ]
分	[ 6 , 1 , 8 , 3 ] 、 [ 5 , 9 , 2 , 4 ]
分	[ 6 , 1 ] 、 [ 8 , 3 ] 、 [ 5 , 9 ] 、 [2 , 4 ]
分	[ 6 ]、 [1 ] 、 [ 8 ]、 [ 3 ] 、 [ 5 ] 、 [9 ] 、 [2 ]、 [ 4 ]
治	[1 , 6 ] 、[ 3 , 8 ] 、 [ 5 , 9 ] 、[ 2 , 4 ]
治	[1 ， 3 ， 6 ，8 ] 、 [ 2， 4 ，5 ，9 ]
治	[ 1，2，3，4，5，6，8，9 ]

代码实现

public class Test {
    public static void main(String[] args) {
        int[] arr = { 6 , 1 , 8 , 3 , 5 , 9 , 2 , 4 };
        int[] temp = new int[arr.length];//归并排序需要额外的数组空间
        mergeSort(arr, 0, arr.length - 1, temp);
        //将数组分成最小单元
        System.out.println(Arrays.toString(arr));
    }
 
    //分
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right) / 2;//中间索引
            mergeSort(arr, left, mid, temp);//向左递归分解数组
            mergeSort(arr, mid + 1, right, temp);//向右递归分解数组
            merge(arr, left, mid, right, temp);//分解完成后将数组进行合并
        }
    }
 
    //治
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        int i = left;//i为指向左边序列第一个元素的索引
        int j = mid + 1;//j为指向右边序列第一个元素的索引
        int t = 0;//指向临时temp数组的当前索引
 
        //先把左右两边有序数据按规则存入temp数组中,直到有一边的数据全部填充temp中
        while (i <= mid && j <= right) {
            if (arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t++;
                i++;
            } else {
                temp[t] = arr[j];
                t++;
                j++;
            }
        }
 
        //将有剩余数据的一边全部存入temp中
        while (i <= mid) {//左边序列有剩余元素
            temp[t] = arr[i];
            t++;
            i++;
        }
        while (j <= right) {//右边序列有剩余元素
            temp[t] = arr[j];
            t++;
            j++;
        }
        t = 0;
        int tempLeft = left;
        while (tempLeft <= right) {
            arr[tempLeft] = temp[t];
            t++;
            tempLeft++;
        }
    }
}