一、算法核心

1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。
2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

二、经典例题

1.226. 翻转二叉树

（1）思想

注意只要把每一个节点的左右孩子翻转一下，就可以达到整体翻转的效果
这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子翻转了两次！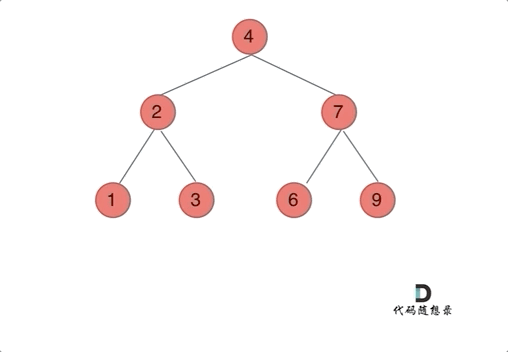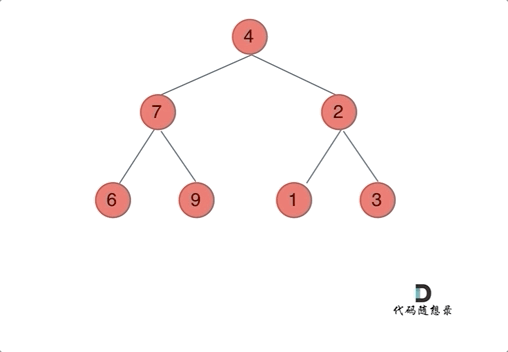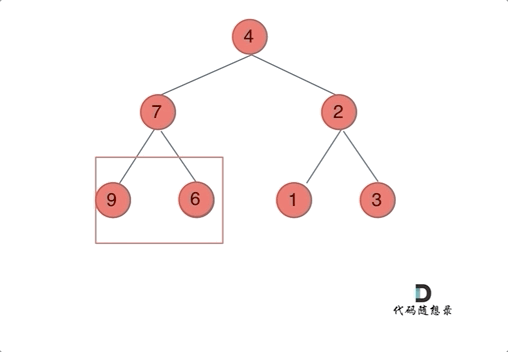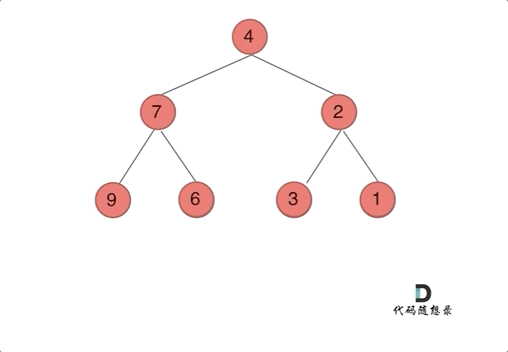

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) return root;
        swap(root->left, root->right);  // 中
        invertTree(root->left);         // 左
        invertTree(root->right);        // 右
        return root;
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$，算上了递归系统栈占用的空间

2.101. 对称二叉树

（1）思想

递归三部曲:

1. 确定递归函数的参数和返回值
   因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较的是两个树，参数自然也是左子树节点和右子树节点。

2. 确定终止条件
   要比较两个节点数值相不相同，首先要把两个节点为空的情况弄清楚！否则后面比较数值的时候就会操作空指针了。节点为空的情况有：（注意我们比较的其实不是左孩子和右孩子，所以如下我称之为左节点右节点）
   左节点为空，右节点不为空，不对称，return false
   左不为空，右为空，不对称 return false
   左右都为空，对称，返回true
   此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：
   左右都不为空，比较节点数值，不相同就return false
   此时左右节点不为空，且数值也不相同的情况我们也处理了。

3. 确定单层递归的逻辑
   此时才进入单层递归的逻辑，单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
   比较内侧是否对称，传入左节点的右孩子，右节点的左孩子。
   如果左右都对称就返回true ，有一侧不对称就返回false 。

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool compare(TreeNode* left,TreeNode* right) {
        if (left == nullptr && right != nullptr) return false;
        else if (left != nullptr && right == nullptr) return false;
        else if (left == nullptr && right == nullptr) return true;
        else if (left -> val != right -> val) return false;
        else return (compare(left -> left,right -> right))&& compare(left->right, right->left);
    }
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return true;
        return compare(root->left, root->right);
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$

3.222. 完全二叉树的节点个数

（1）思想

1. 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回以该节点为根节点二叉树的节点数量，所以返回值为int类型。
2. 确定终止条件：如果为空节点的话，就返回0，表示节点数为0。
3. 确定单层递归的逻辑：先求它的左子树的节点数量，再求右子树的节点数量，最后取总和再加一 （加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getNodesNum(TreeNode* cur) {
        if (cur == NULL) return 0;
        int leftNum = getNodesNum(cur -> left);
        int rightNum = getNodesNum(cur -> right);
        int treeNum = leftNum + rightNum + 1;
        return treeNum;
}
    int countNodes(TreeNode* root) {
        return getNodesNum(root);
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(logn)$，算上了递归系统栈占用的空间

4.110.平衡二叉树

（1）思想

那是因为代码的逻辑其实是求的根节点的高度，而根节点的高度就是这棵树的最大深度，所以才可以使用后序遍历。

1. 明确递归函数的参数和返回值
   参数：当前传入节点。 返回值：以当前传入节点为根节点的树的高度。
2. 明确终止条件
   递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0
3. 明确单层递归的逻辑
   如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？当然是其左子树高度和其右子树高度的差值。

（2）代码

class Solution {
public:
    // 返回以该节点为根节点的二叉树的高度，如果不是平衡二叉树了则返回-1
    int getHeight(TreeNode* node) {
        if (node == NULL) {
            return 0;
        }
        int leftHeight = getHeight(node->left);
        if (leftHeight == -1) return -1;
        int rightHeight = getHeight(node->right);
        if (rightHeight == -1) return -1;
        return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
    }
    bool isBalanced(TreeNode* root) {
        return getHeight(root) == -1 ? false : true;
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$，算上了递归系统栈占用的空间

5.257. 二叉树的所有路径

（1）思想

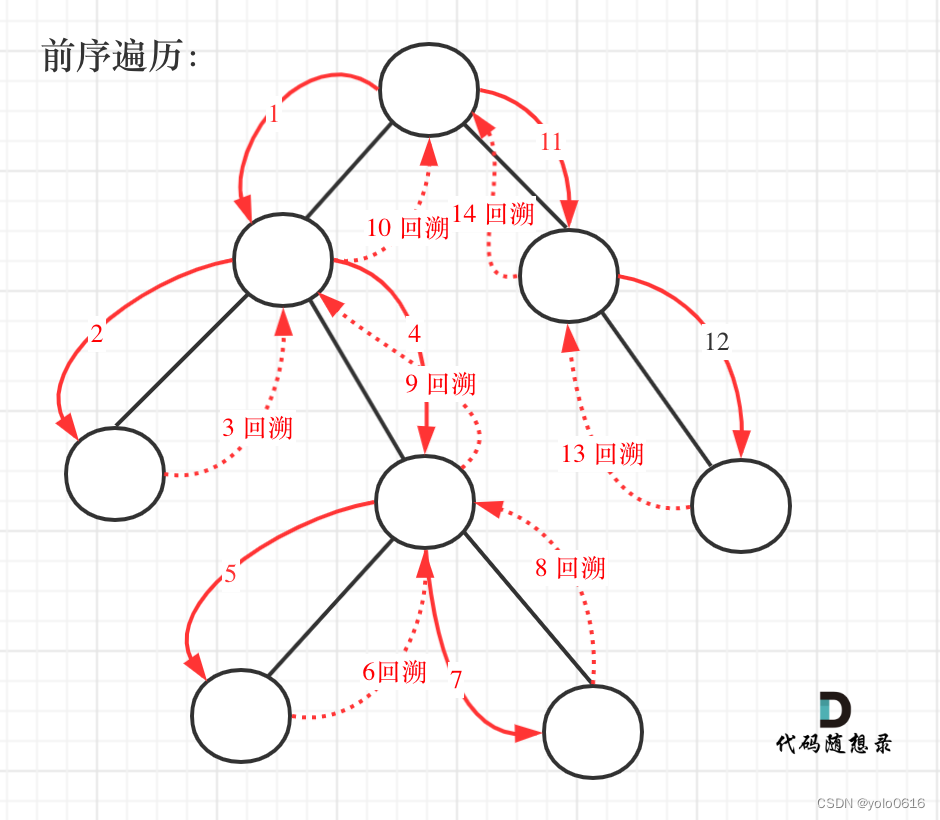
这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。
在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。

1. 递归函数参数以及返回值

要传入根节点，记录每一条路径的path，和存放结果集的result，这里递归不需要返回值，代码如下：
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)

2. 确定递归终止条件

if (cur->left == NULL && cur->right == NULL) {
    终止处理逻辑
}

3. 确定单层递归逻辑

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
        path.push_back(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中 
        if (cur -> left == nullptr && cur -> right == nullptr) {
            string temp;
            for (int i = 0; i < path.size() - 1; i ++) {
                temp += to_string(path[i]);
                temp += "->";
            }
            temp += to_string(path[path.size() - 1]);
            result.push_back(temp);
            return;
        }
        if (cur->left) { // 左 
            traversal(cur->left, path, result);
            path.pop_back(); // 回溯
        }
        if (cur->right) { // 右
            traversal(cur->right, path, result);
            path.pop_back(); // 回溯
        }
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        vector<int> path;
        if (root == nullptr) return result;
        traversal(root,path,result);
        return result;
    }
};

（3）复杂度分析

时间复杂度：$O(n^2)$
空间复杂度：$O(n^2)$，算上了递归系统栈占用的空间

6.404. 左叶子之和

（1）思想

1. 确定递归函数的参数和返回值
   判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int
   使用题目中给出的函数就可以了。
2. 如果遍历到空节点，那么左叶子值一定是0
   注意，只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点，那其左叶子也必定是0，那么终止条件为：
3. 确定单层递归的逻辑
   当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumProcess(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right== NULL) return 0;
        int leftValue = sumOfLeftLeaves(root->left);  //   左
        if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) 
     // 左叶子节点处理逻辑
            leftValue = root->left->val;
        int rightValue = sumOfLeftLeaves(root->right);  // 右
        int sum = leftValue + rightValue;               // 中
        return sum;
    }
    int sumOfLeftLeaves(TreeNode* root) {
        return sumProcess(root);
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$，算上了递归系统栈占用的空间

7.513. 找树左下角的值

（1）思想

（2）代码

dfs
class Solution {
public:
    int maxDepth = INT_MIN;
    int result;
    void traversal(TreeNode* root, int depth) {
        if (root->left == NULL && root->right == NULL) {
            if (depth > maxDepth) {
                maxDepth = depth;
                result = root->val;
            }
            return;
        }
        if (root->left) {
            depth++;
            traversal(root->left, depth);
            depth--; // 回溯
        }
        if (root->right) {
            depth++;
            traversal(root->right, depth);
            depth--; // 回溯
        }
        return;
    }
    int findBottomLeftValue(TreeNode* root) {
        traversal(root, 0);
        return result;
    }
};
bfs
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        int result = 0;
        if (root == nullptr) return 0;
        queue<TreeNode*> que;
        que.push(root);
        while (que.size()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                auto temp = que.front();
                que.pop();
                if (i == 0) result = temp -> val; 
                if (temp->left) que.push(temp ->left);
                if (temp->right) que.push(temp ->right);
            }
        }
        return result;
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$，算上了递归系统栈占用的空间

8. 112.路经总和

（1）思想

1. 确定递归函数的参数和返回类型
   参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。

• 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值
• 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。
• 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）

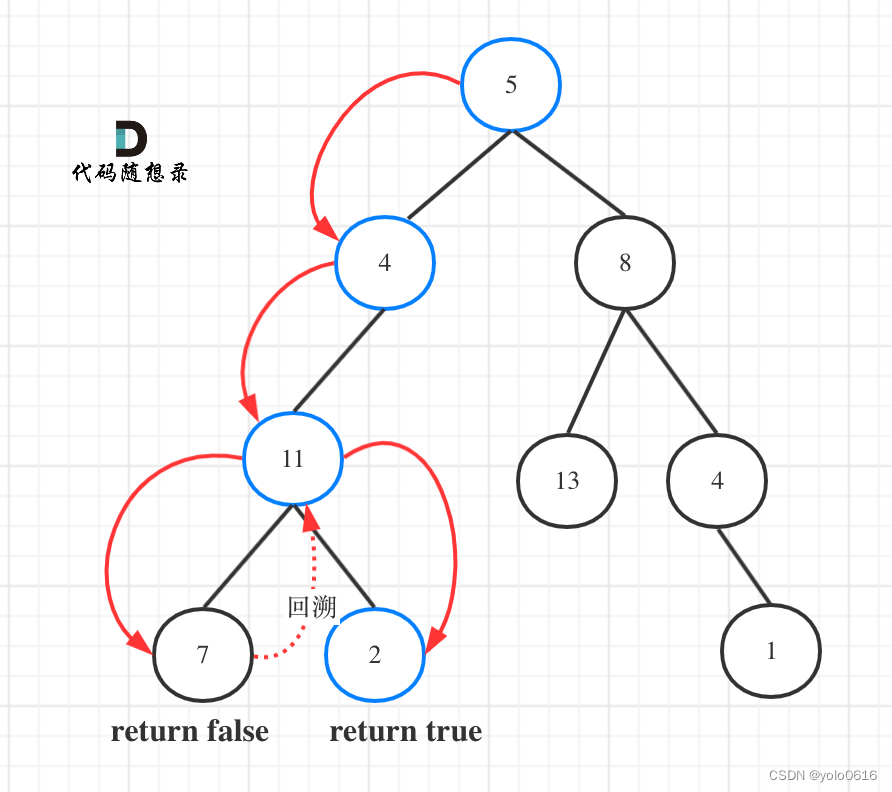
图中可以看出，遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。
2. 确定终止条件
首先计数器如何统计这一条路径的和呢？
不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。
如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。
如果遍历到了叶子节点，count不为0，就是没找到。
递归终止条件代码如下

if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
if (!cur->left && !cur->right) return false; // 遇到叶子节点而没有找到合适的边，直接返回

3. 确定单层递归的逻辑
   因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。
   递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。

（2）代码

class Solution {
private:
    bool traversal(TreeNode* cur, int count) {
        if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
        if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回

        if (cur->left) { // 左
            count -= cur->left->val; // 递归，处理节点;
            if (traversal(cur->left, count)) return true;
            count += cur->left->val; // 回溯，撤销处理结果
        }
        if (cur->right) { // 右
            count -= cur->right->val; // 递归，处理节点;
            if (traversal(cur->right, count)) return true;
            count += cur->right->val; // 回溯，撤销处理结果
        }
        return false;
    }

public:
    bool hasPathSum(TreeNode* root, int sum) {
        if (root == NULL) return false;
        return traversal(root, sum - root->val);
    }
};

（3）复杂度分析

时间复杂度：$O(N)$
空间复杂度：$O(H)$，其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(log⁡N)。

9. 113. 路径总和 II

（1）思想

（2）代码

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(logn)$，算上了递归系统栈占用的空间

9. 113. 路径总和 II

（1）思想

113.路径总和ii要遍历整个树，找到所有路径，所以递归函数不要返回值！

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
    void tra(TreeNode* root,int count) {
        if (!root -> left && !root ->right && count == 0) {
            res.push_back(path);
            return;
        }
        if (!root -> left && !root ->right)
            return;
        if (root -> left) {
            path.push_back(root -> left -> val);
            count -= root -> left -> val;
            tra(root -> left,count);
            count += root -> left -> val;
            path.pop_back();
        }
         if (root -> right) {
            path.push_back(root -> right -> val);
            count -= root -> right -> val;
            tra(root -> right,count);
            count += root -> right -> val;       
            path.pop_back();
        }
        
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        if (root == nullptr)
            return res;
        path.push_back(root->val);
        tra(root,targetSum - root -> val);
        
        return res;
    }
};

（3）复杂度分析

时间复杂度：$O(N)$
空间复杂度：$O(H)$，其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(log⁡N)。

10. 106. 从中序与后序遍历序列构造二叉树

（1）思想

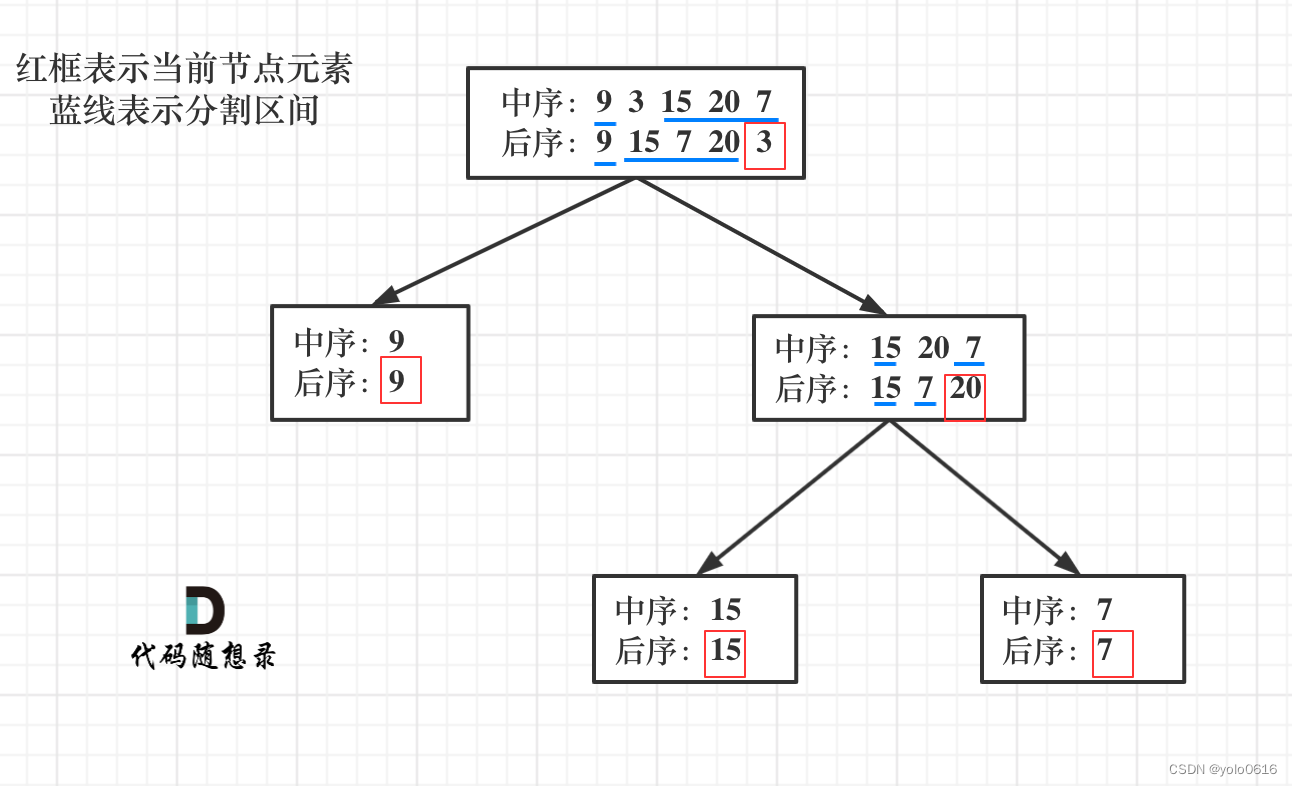
来看一下一共分几步：
// 中序：左根右
// 后序：左右根
第一步：如果数组大小为零的话，说明是空节点了。
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
        if (postorder.size() == 0) return nullptr;

        int rootValue = postorder[postorder.size() - 1];
        TreeNode* root = new TreeNode(rootValue);
        // 叶子节点
        if (postorder.size() == 1) return root;

        int delimiterIndex;
        // 找到中序遍历的切割点
        for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex ++) {
             if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 左闭右开区间：[0, delimiterIndex)
        vector<int> leftInorder(inorder.begin(),inorder.begin() + delimiterIndex);
        vector<int> rightInorder (inorder.begin() + delimiterIndex + 1,inorder.end());
        // postorder 舍弃末尾元素
        postorder.resize(postorder.size() - 1);
        // 切割后序数组
        // 依然左闭右开，注意这里使用了左中序数组大小作为切割点
        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
        vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

        root->left = traversal(leftInorder, leftPostorder);
        root->right = traversal(rightInorder, rightPostorder);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        // 中序：左根右
        // 后序：左右根
        if (inorder.size() == 0 || postorder.size() == 0) return nullptr;
        return traversal(inorder,postorder);
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$，算上了递归系统栈占用的空间

11. 105. 从前序与中序遍历序列构造二叉树

（1）思想

（2）代码

class Solution {
private:
        TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
        if (preorderBegin == preorderEnd) return NULL;

        int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
        TreeNode* root = new TreeNode(rootValue);

        if (preorderEnd - preorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 中序左区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 中序右区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割前序数组
        // 前序左区间，左闭右开[leftPreorderBegin, leftPreorderEnd)
        int leftPreorderBegin =  preorderBegin + 1;
        int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
        // 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
        int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
        int rightPreorderEnd = preorderEnd;

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  preorder, leftPreorderBegin, leftPreorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);

        return root;
    }

public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (inorder.size() == 0 || preorder.size() == 0) return NULL;

        // 参数坚持左闭右开的原则
        return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$，算上了递归系统栈占用的空间

12. 654. 最大二叉树

（1）思想

我们用递归函数 construct(nums,left,right)表示对数组 nums中从 nums[left] 到 nums[right]的元素构建一棵树。我们首先找到这一区间中的最大值，记为 num中从 nums[maxValue]，这样就确定了根节点的值。随后我们就可以进行递归：

左子树为 construct(nums,left,maxValue−1)

右子树为 construct(nums,maxValue+1,right)

当递归到一个无效的区间（即 left>right）时，便可以返回一棵空的树。

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return construct(nums,0,nums.size() - 1);
    }
    TreeNode* construct(const vector<int>&nums,int left,int right) {
        if (left > right) {
            return nullptr;
        }
        int maxValue = left;
        for (int i = left; i <= right; i++) {
            if (nums[i] > nums[maxValue]) {
                maxValue = i;
            }
        }
        TreeNode* node = new TreeNode(nums[maxValue]);
        node->left = construct(nums, left, maxValue - 1);
        node->right = construct(nums, maxValue + 1, right);
        return node;
    }
};

（3）复杂度分析

时间复杂度：$O(n^2)$其中 n 是数组 $nums$的长度。在最坏的情况下，数组严格递增或递减，需要递归 $n$ 层，第$i(0\le i<n)$层需要遍历$n-i$个元素以找出最大值，总时间复杂度为$O(n^2)$

空间复杂度：$O(n)$，算上了递归系统栈占用的空间

13. 617. 合并二叉树

（1）思想

1. 确定递归函数的参数和返回值：
   首先要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。
2. 确定终止条件：
   因为是传入了两个树，那么就有两个树遍历的节点t1 和 t2，如果t1 == NULL 了，两个树合并就应该是 t2 了（如果t2也为NULL也无所谓，合并之后就是NULL）。
   反过来如果t2 == NULL，那么两个数合并就是t1（如果t1也为NULL也无所谓，合并之后就是NULL）。
3. 确定单层递归的逻辑：
   单层递归的逻辑就比较好写了，这里我们重复利用一下t1这个树，t1就是合并之后树的根节点（就是修改了原来树的结构）。

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (root1 == nullptr)
            return root2;
        if (root2 == nullptr)
            return root1;
        auto merge = new TreeNode(root1 -> val + root2 -> val);
        merge -> left = mergeTrees(root1 -> left,root2 -> left);
        merge -> right = mergeTrees(root1 -> right,root2 -> right);
        return merge;
    }
};

（3）复杂度分析

时间复杂度：$O(min(m,n)$
空间复杂度：$O(min(m,n)$，算上了递归系统栈占用的空间

14. 700.二叉搜索树中的搜索

（1）思想

二叉搜索树满足如下性质：

左子树所有节点的元素值均小于根的元素值；
右子树所有节点的元素值均大于根的元素值。
据此可以得到如下算法：

若 root为空则返回空节点；
若 val=root.val,则返回 root；
若 val<root.val,递归左子树；
若 val>root.val,递归右子树。

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
递归：
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == nullptr) return nullptr;
        if (root -> val == val) return root;
        TreeNode* result = nullptr;
        if (root -> val < val) result = searchBST(root -> right,val);
        if (root -> val > val) result = searchBST(root -> left,val);
        return result;
    }
};
迭代：
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        while (root != NULL) {
            if (root->val > val) root = root->left;
            else if (root->val < val) root = root->right;
            else return root;
        }
        return NULL;
    }
};

（3）复杂度分析

时间复杂度：$O(N)$
空间复杂度：$O(N)$，算上了递归系统栈占用的空间

时间复杂度：$O(N)$
空间复杂度：$O(1)$，算上了递归系统栈占用的空间

15. 98. 验证二叉搜索树

（1）思想

启示我们在中序遍历的时候实时检查当前节点的值是否大于前一个中序遍历到的节点的值即可。如果均大于说明这个序列是升序的，整棵树是二叉搜索树，否则不是，下面的代码我们使用栈来模拟中序遍历的过程。

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
long long maxVal = LONG_MIN; 
    bool isValidBST(TreeNode* root) {
        if (root == nullptr) return true;
        bool left = isValidBST(root -> left);
        if (maxVal < root -> val) maxVal = root -> val;
        else return false;
        bool right = isValidBST(root -> right);
        return left && right;
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$，算上了递归系统栈占用的空间

17. 501. 二叉搜索树中的众数

（1）思想

1. 这个树都遍历了，用map统计频率
2. 把统计的出来的出现频率（即map中的value）排个序
3. 取前面高频的元素

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> res;
    unordered_map<int,int> mp;
    void process(TreeNode* root) {
        if (root == nullptr) return ;
        process(root -> left);
        mp[root -> val] ++;
        process(root -> right);
    }
    bool static cmp(const pair<int,int>& a,const pair<int,int> &b) {
        return a.second > b.second;
    }
    vector<int> findMode(TreeNode* root) {
        process(root);
        vector<pair<int, int>> vec(mp.begin(), mp.end());
        sort(vec.begin(), vec.end(), cmp); // 给频率排个序
        res.push_back(vec[0].first);
        for (int i = 1; i < vec.size(); i++) {
            if (vec[i].second == vec[0].second) res.push_back(vec[i].first);
            else break;
        }
        return res;
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$，算上了递归系统栈占用的空间

18. 530. 二叉搜索树的最小绝对差

（1）思想

朴素的方法是经过一次中序遍历将值保存在一个数组中再进行遍历求解，我们也可以在中序遍历的过程中用 pre变量保存前驱节点的值，这样即能边遍历边更新答案，不再需要显式创建数组来保存，需要注意的是 pre的初始值需要设置成任意负数标记开头，下文代码中设置为 −1。

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
int result = INT_MAX;
TreeNode* pre = NULL;
    void isBST(TreeNode* root) {
        if (root == nullptr) return;
        isBST(root -> left);
        if (pre != nullptr) {
            result = min(result,root -> val - pre -> val);
        }
        pre = root;
        isBST(root -> right);
    }
    int getMinimumDifference(TreeNode* root) {
        if (root == nullptr) return false;
        isBST(root);
        return result;
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$，算上了递归系统栈占用的空间

19. 236. 二叉树的最近公共祖先

（1）思想

遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了。
那么二叉树如何可以自底向上查找呢？
回溯啊，二叉树回溯的过程就是从低到上。
后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑。
接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。
首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。
即情况一：

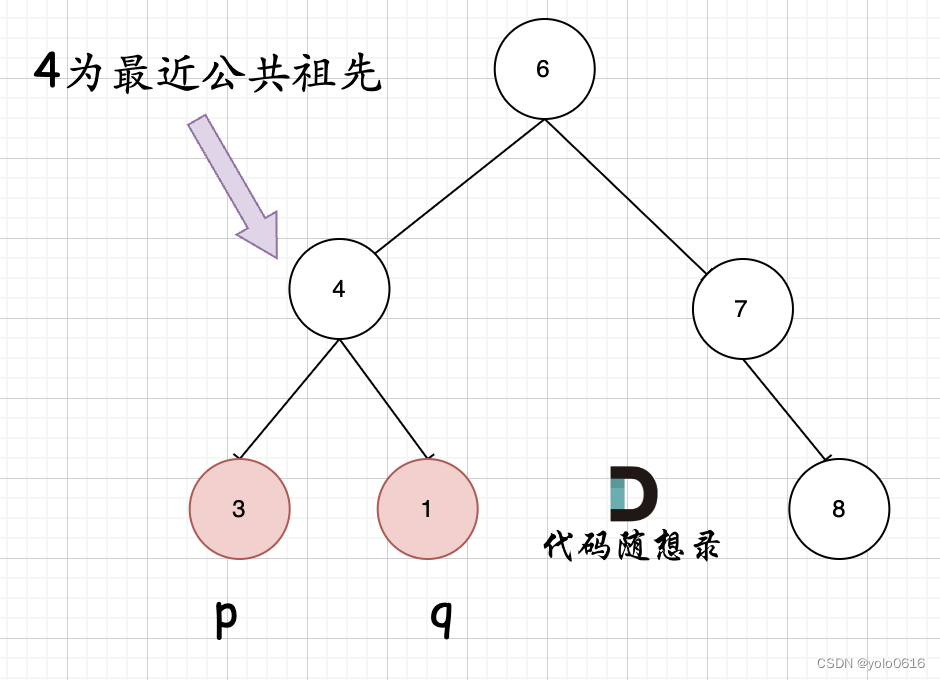
但是很多人容易忽略一个情况，就是节点本身p(q)，它拥有一个子孙节点q§。 情况二：

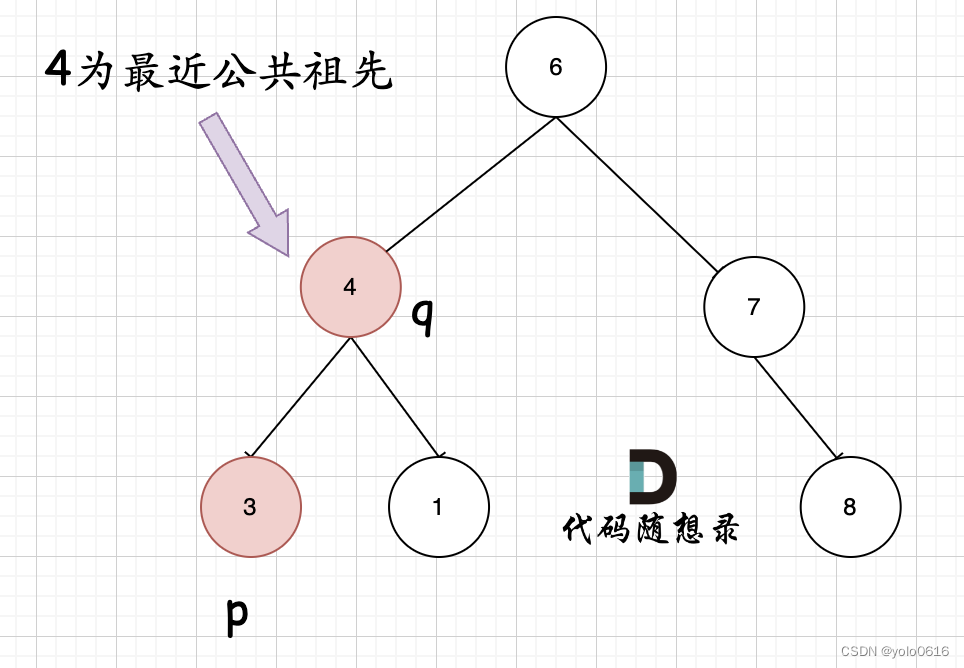
1. 确定递归函数返回值以及参数
   需要递归函数返回值，来告诉我们是否找到节点q或者p，那么返回值为bool类型就可以了。但我们还要返回最近公共节点，可以利用上题目中返回值是TreeNode * ，那么如果遇到p或者q，就把q者p返回，返回值不为空，就说明找到了q或者p。

2. 确定终止条件
   遇到空的话，因为树都是空了，所以返回空。
   那么我们来说一说，如果 root == q，或者 root == p，说明找到 q p ，则将其返回，这个返回值，后面在中节点的处理过程中会用到，那么中节点的处理逻辑，下面讲解。

3. 确定单层递归逻辑
   
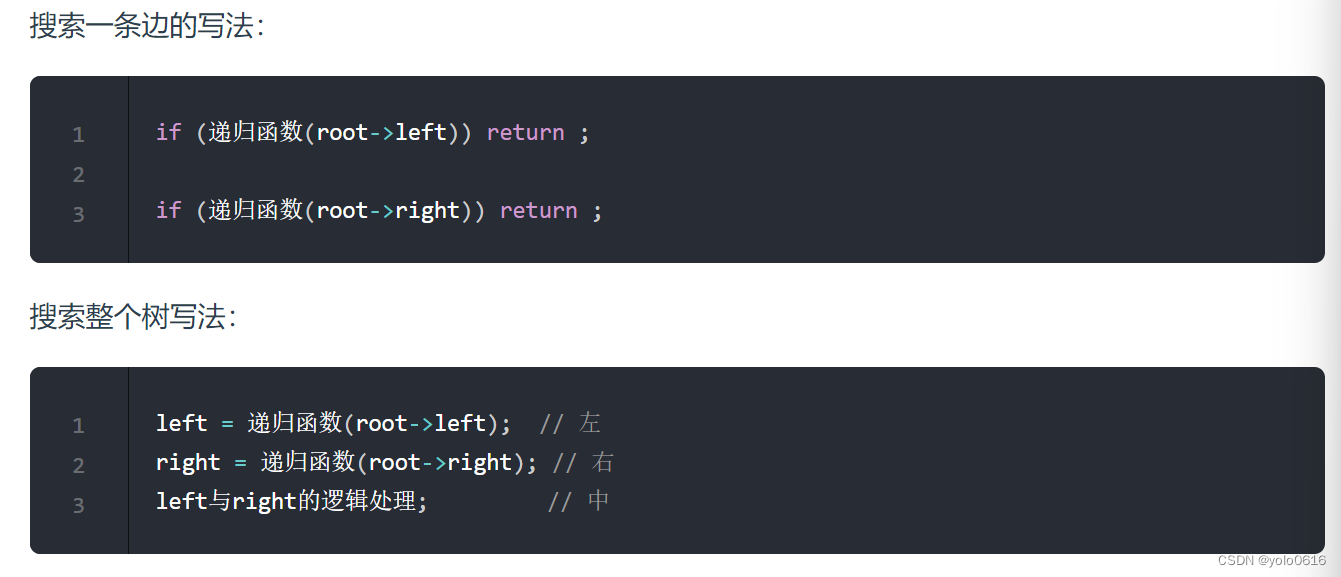
   在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

（2）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
int result = INT_MAX;
TreeNode* pre = NULL;
    void isBST(TreeNode* root) {
        if (root == nullptr) return;
        isBST(root -> left);
        if (pre != nullptr) {
            result = min(result,root -> val - pre -> val);
        }
        pre = root;
        isBST(root -> right);
    }
    int getMinimumDifference(TreeNode* root) {
        if (root == nullptr) return false;
        isBST(root);
        return result;
    }
};

（3）复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(n)$，算上了递归系统栈占用的空间