一、线性规划模型（Lingo）

1.线性规划问题（模板）

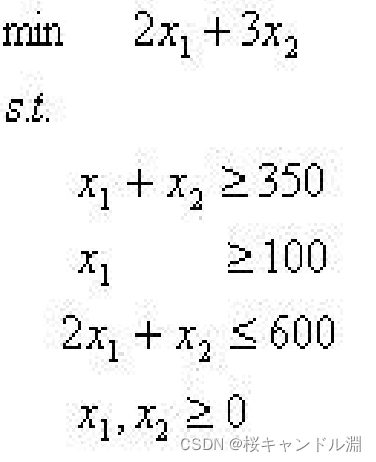
model:
min = 2 *x1 + 3 *x2;
x1 + x2 >= 350;
x1 >= 100;
2 * x1 + x2 <= 600;
end

2.求解最优化问题

model:
min=fx+gy;
fx=@if(x #gt# 0,100,0)+2*x;
gy=@if(y #gt# 0,60+3*y,2*y);
x+y>=30;
end

3.包装箱平板车问题

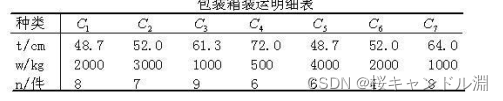
这是对于我们模型的约束条件的建模

下面为本道题的lingo代码

model:
sets:
!定义我们的其中规格的包装箱,分别有t,w,n三个属性;
type/1..7/:t,w,n;
!定义我们的平板车,分别有长度和载重两个属性;
car/1..2/:cl,cw;
matrix(type,car):x;
endsets

data:
t=48.7,52,61.3,72,48.7,52,64;
w=2000 ,3000,1000,500,4000,2000,1000;
n=8,7,9,6,6,4,8;
cl=020,1020;
cw=40000,40000;
s=302.7;
enddata

max=@sum(type(i):t(i)*(x(i,1)+x(i,2)));
@for(type(i):x(i,1)+x(i,2)<=n(i));

@for(car(j):@sum(type(i):t(i)*x(i,j))<=cl(j));
@for(car(j):@sum(type(i):w(i)*x(i,j))<=cw(j));
@sum(type(i)|i#ge#5:t(i)*(x(i,1)+x(i,2)))<=s;
@for(matrix(i,j):@gin(x(i,j)));

end

4.职员时序安排问题

model:
sets:
days/mon..sun/:r,start;
endsets
data:
!每天所需的最少职员数;
r=20 16 13 16 19 14 12;
enddata
!最小化每周所需职员数;
min=z;
!对于每一天开始工作的员工数量进行遍历
z=@sum(days:start);
!遍历每一天的数据进行加和，因为每一个员工都是会工作5天的，所以今天要工作的员工是全部的员工z减去与今天星期相同的上一周的下一天和下下一天的员工，他们加起来的和需要大于每天所需的最少职员数
@for(days(i):z-start(@wrap(i+1,7))-start(@wrap(i+2,7))>= r(i));
end

5.运输问题

使用Lingo软件计算6个发点和8个收点的最小费用运输问题。产销单位运价如下表。

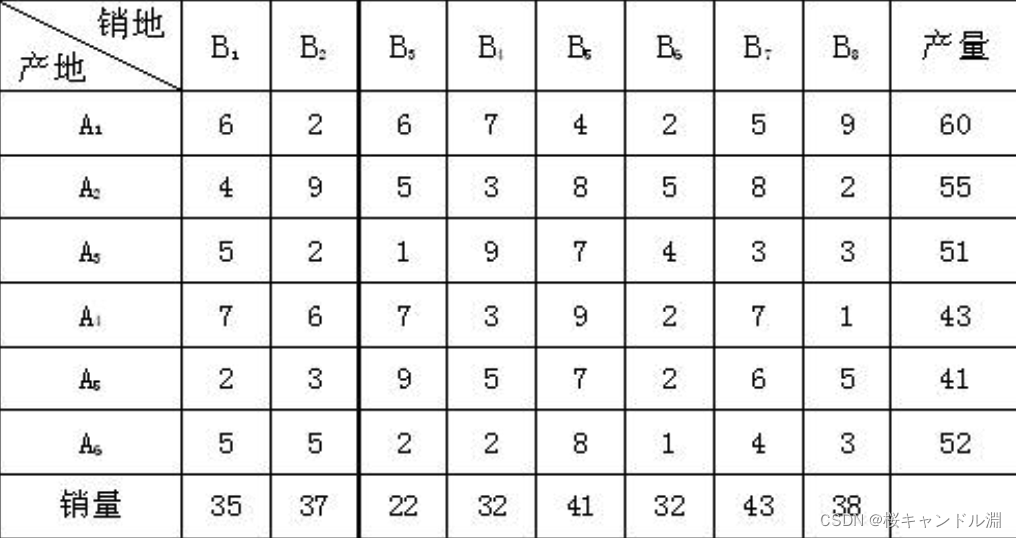
model:
!6发点8收点运输问题;
sets:
    warehouses/wh1..wh6/:capacity;
    vendors/v1..v8/:demand;
    links(warehouses,vendors):cost,volume;
endsets
!目标函数;
min=@sum(links:cost*colume);
!需求约束;
@for(vendors(J):
    @sum(warehouses(I):volume(I,J))=demand(J));
!产量约束;
@for(warehouses(I):
    @sum(vendors(J):volume(I,J))<=capacity(I));
!这是数据;
data:
    capacity=60 55 51 43 41 52;
    demand=35 37 22 32 41 32 43 38;
    cost=6 2 6 7 4 2 9 5
 	4 9 5 3 8 5 8 2
	5  2 1 9 7 4 3 3 
	7 6 7 3 9 2 7 1
	2 3 9 5 7 2 6 5 
	5 5 2 2 8 1 4 3;
enddata
end

6.排菜单问题

某疗养院营养师要为某类病人拟定本周蔬菜类菜单，当前可供选择的蔬菜品种、价格和营养成分含量，以及病人所需营养成分的最低数量见下表所示。病人每周需14份蔬菜，为了口味的原因，规定一周内的卷心菜不多于2份，胡萝卜不多于3份，其他蔬菜不多于4份，且蔬菜都至少1份。在满足要求的前提下，制定费用最少的一周菜单方案。
当前可供蔬菜养分含量（mg）和价格
铁 | 磷 |维生素A |维生素C |烟酸 |每份价格（元）|

单位所含养分量	铁	磷	维生素A	维生素C	烟酸	每份价格（元）
青豆	0.45	20	415	22	0.3	2.1
胡萝卜	0.45	28	4065	5	0.35	1.0
花菜	0.65	40	850	43	0.6	1.8
卷心菜	0.4	25	75	27	0.2	1.2
芹菜	0.5	26	76	48	0.4	2.0
土豆	0.5	75	235	8	0.6	1.2
每周最低需求	6	125	12500	345	5

编写Lingo程序求解上述问题。

model:
!配菜单;
sets:
vege/1..6/:price,ulimit,dlimit,num;
nutr/1..5/:need;
link(vege,nutr):content;
endsets

data:
price=2.1 1 1.8 1.2 2 1.2;
ulimit=4 3 4 2 4 4;
dlimit=1 1 1 1 1 1;
need=6	125	12500	345	5	;
content=
0.45	20	415	22	0.3	
0.45	28	4065	5	0.35	
0.65	40	850	43	0.6	
0.4	25	75	27	0.2	
0.5	26	76	48	0.4	
0.5	75	235	8	0.6	;
enddata

min=@sum(vege:price*num);
@for(nutr(j):@sum(vege(i):content(i,j)*num(i))>=need(j));
@for(vege:num>=dlimit);
@for(vege:num<=ulimit);
@sum(vege:num)=14;

end

7.工地施工问题

第一问

model:
sets:
lc/A,B/:px,py,e;
gd/1..6/:x,y,d;
links(lc,gd):c;
endsets
data:
px=5 2;
py=1 7;
e=20 20;
x=1.25 8.75 0.5 5.75 3 7.25;
y=1.25 0.75 4.75 5 6.5 7.75;
d=3 5 4 7 6 11;
enddata
min=@sum(links(i,j):c(i,j)*((px(i)-x(j))^2+(py(i)-y(j))^2)^(1/2));
@for(gd(j):@sum(lc(i):c(i,j))=d(j));
@for(lc(i):@sum(gd(j):c(i,j))<=e(i));
end

第二问

model:
sets:
lc/A,B/:px,py,e;
gd/1..6/:x,y,d;
links(lc,gd):c;
endsets
data:
x=1.25 8.75 0.5 5.75 3 7.25;
y=1.25 0.75 4.75 5 6.5 7.75;
d=3 5 4 7 6 11;
e=20 20;
enddata
min=@sum(links(i,j):c(i,j)*((px(i)-x(j))^2+(py(i)-y(j))^2)^(1/2));
@for(gd(j):@sum(lc(i):c(i,j))=d(j));
@for(lc(i):@sum(gd(j):c(i,j))<=e(i));
end

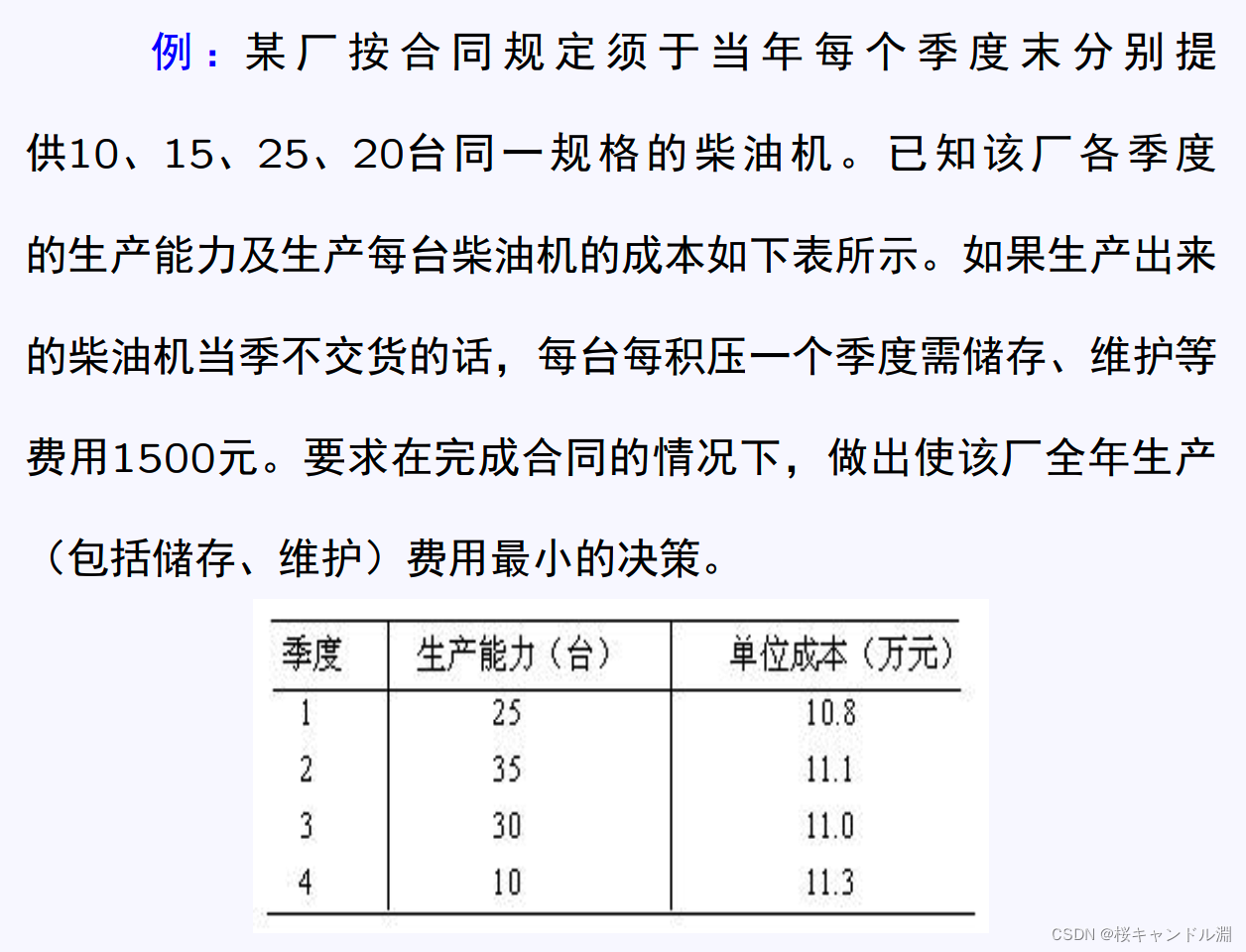
8.生产计划优化研究（柴油机生产）

某柴油机厂年度产品生产计划的优化研究。某柴油机厂是我国生产中小功率柴油机的重点骨干企业之一。主要产品有2105柴油机、x2105柴油机、x4105柴油机、x4110柴油机、x6105柴油机、x6110柴油机。柴油机生产过程主要分成三大类：热处理、机加工、总装。与产品生产有关的主要因素有单位产品的产值、生产能力、原材料供应量及生产需求情况等。
每种产品的单位产值如表1所示。
表1 各产品的单位产值

序号	产品型号及名称	单位产值（元）
1	2105柴油机	5400
2	x2105柴油机	6500
3	x4105柴油机	12000
4	x4110柴油机	14000
5	x6105柴油机	18500
6	x6110柴油机	20000

为简化问题，根据一定时期的产量与所需工时，测算了每件产品所需的热处理、机加工、总装工时，如表2所示。
表2 单位产品所需工时

序号	产品型号及名称	热处理	机加工	总装
1	2105柴油机	10.58	14.58	17.08
2	x2105柴油机	11.03	7.05	150
3	x4105柴油机	29.11	23.96	29.37
4	x4110柴油机	32.26	27.7	33.38
5	x6105柴油机	37.63	29.36	55.1
6	x6110柴油机	40.84	40.43	53.5

同时，全厂所能提供的总工时如表3所示。
表3 各工序所能提供的工时

工序名称	热处理	机加工	总装
全年提供总工时	120000	95000	180000

产品原材料主要是生铁、焦炭、废钢、钢材四大类资源。原材料供应最大的可能值如表4所示。
表4 原材料最大供应量

原材料名称 生铁（吨）	焦炭（吨）	废钢（吨）	钢材（吨）
最大供应量	1562	951	530

单位产品原材料消耗情况如表5所示。

表5 单位产品原材料消耗情况

序号	产品型号及名称	生铁（吨）	焦炭（吨）	废钢（吨）	钢材（吨）
1	2105柴油机	0.18	0.11	0.06	0.04
2	x2105柴油机	0.19	0.12	0.06	0.04
3	x4105柴油机	0.35	0.22	0.12	0.08
4	x4110柴油机	0.36	0.23	0.13	0.09
5	x6105柴油机	0.54	0.33	0.18	0.12
6	x6110柴油机	0.55	0.34	0.19	0.13

依照历年销售情况、权威部门的市场预测及企业近期进行的生产调查结果，可以分别预测出各种型号柴油机今年的市场需求量，如表6所示。
表6 各种型号柴油机今年的市场需求量

序号	产品型号及名称	生产能力（台）	市场需求量（台）
1	2105柴油机	8000	8000
2	x2105柴油机	2000	1500
3	x4105柴油机	4000	4000
4	x4110柴油机	2000	1000
5	x6105柴油机	3000	3000
6	x6110柴油机	3000	2000

根据以上资料，请制定较为科学的产品生产计划。用Lingo软件求解上述问题。

model:
sets:
limit/1..6/:method1,method2,method3,material1,material2,material3,material4,x,demand,output;
endsets
max=@sum(limit:output*x);
data:
method1=10.58,11.03,29.11,32.26,27.63,40.84;
method2=14.58,7.05,23.96,27.7,29.36,40.43;
method3=17.08,150,29.37,33.38,55.1,53.5;

material1=0.18,0.19,0.35,0.36,0.54,0.55;
material2=0.11,0.12,0.22,0.23,0.33,0.34;
material3=0.06,0.06,0.12,0.13,0.18,0.19;
material4=0.04,0.04,0.08,0.09,0.12,0.13;

demand=8000,1500,4000,1000,3000,2000;
output=5400,6500,12000,14000,18500,20000;
enddata
@sum(limit(i):method1(i)*x(i))<=120000;
@sum(limit(i):method2(i)*x(i))<=95000;
@sum(limit(i):method3(i)*x(i))<=180000;

@sum(limit(i):material1(i)*x(i))<=1562;
@sum(limit(i):material2(i)*x(i))<=951;
@sum(limit(i):material3(i)*x(i))<=530;
@sum(limit(i):material4(i)*x(i))<=350;

@for(limit(i):x(i)<=demand(i));
@for(limit(i):x(i)>=0);
@for(limit(i):@gin(x(i)));
end

二、线性规划问题（Matlab）

1.线性规划问题（模板题）

方法一

clc,clear
c=[4;3];b=[10;8;7]
a=[2,1;1,1;0,1];lb=zeros(2,1);
[x,fval]=linprog(-c,a,b,[],[],lb)%没有等号约束
y=-fval%目标函数为最大化

方法二

clc,clear
prob=optimproblem('ObjectiveSense','max')

c=[4;3];b=[10;8;7];
a=[2,1;1,1;0,1];lb=zeros(2,1);
x=optimvar('x',2,'LowerBound',0);
prob.Objective=c'*x;
prob.Constraints.con=a*x<=b;
[sol,fval,flag,out]=solve(prob)
sol.x%显示决策变量的值

2.线性规划问题（模板题）

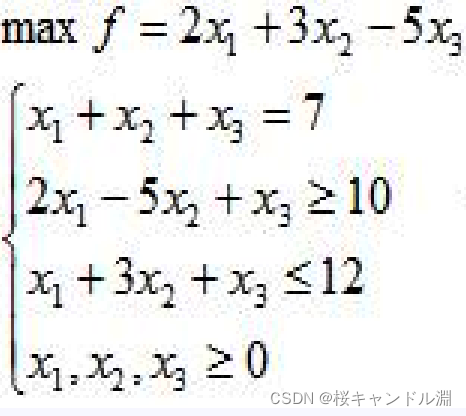
方法一

c=[2;3;-5];
a=[-2,5,-1;1,3,1];
b=[-10;12];
aeq=[1,1,1];
beq=7;
[x,fval]=linprog(-c,a,b,aeq,beq,zeros(3,1))

方法二

clc,clear
prob=optimproblem('ObjectiveSense','max');
x=optimvar('x',3,'LowerBound',0);
prob.Objective=2*x(1)+3*x(2)-5*x(3);
prob.Constraints.con1=x(1)+x(2)+x(3)==7;
prob.Constraints.con2=2*x(1)-5*x(2)+x(3)>=10;
prob.Constraints.con3=x(1)+3*x(2)+x(3)<=12;
[sol,fval,flag,out]=solve(prob),sol.x%显示解

3.仓储问题

捷运公司在下一年度的1~4月的4个月内拟租用仓库堆放物资。仓库租借费用随合同期而定，期限越长，折扣越大。一直各月份所需要的仓库面积列于下表。租借仓库的合同每月初都可办理，每份合同具体规定租用面积和期限。因此该公司可根据需要，在任何一个月初办理租借合同。每次办理时可签一份合同，也可签若干份租用面积和租借期限不同的合同，试确定该公司签订租借合同的最优决策，目的是使所付租借费最少

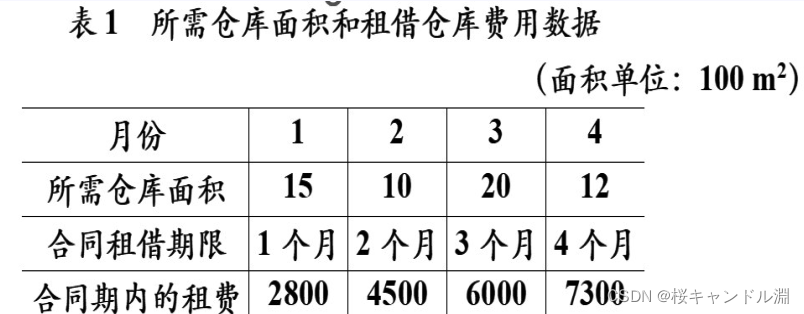
设变量xij表示该公司在第i(i=1,2,3,4)个月初签订的租借期为j(j=1,2,3,4)个月的仓库面积（单位为100平方米）。因5月份起该公司不需要租借仓库，故x24,x33,x42,x43,x44均为0

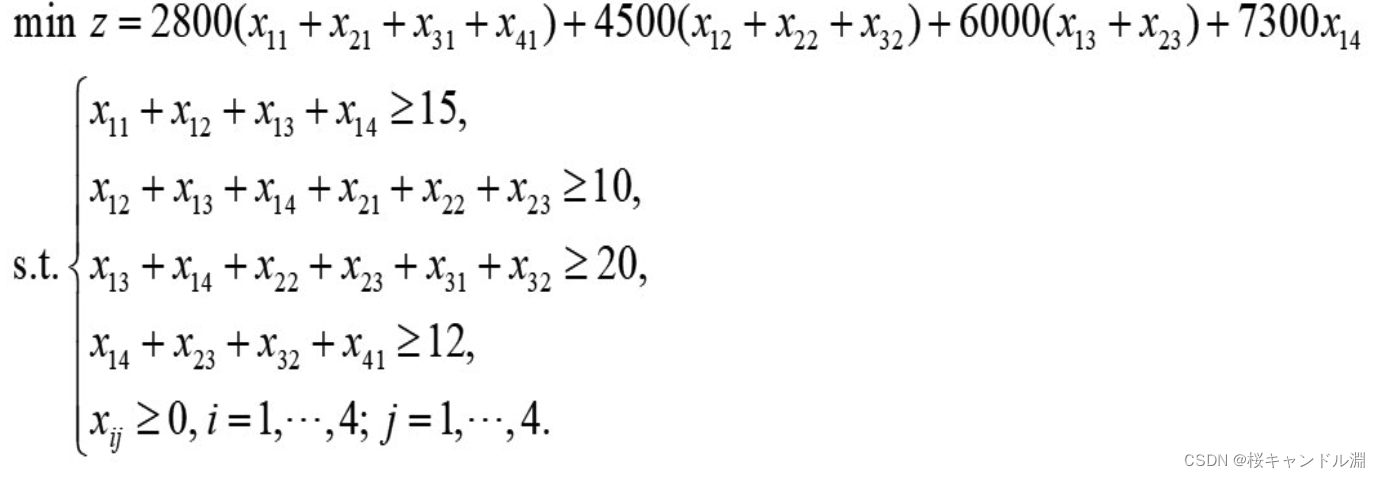
clc,clear
prob=optimproblem;
x=optimvar('x',4,4,'LowerBound',0);
prob.Objective=2800*sum(x(:,1))+4500*sum(x(1:3,2))+6000*sum(x(1:2,3))+7300*x(1,4);
prob.Constraints.con=[sum(x(1,:))>=15
    sum(x(1,2:4))+sum(x(2,1:3))>=10
    x(1,3)+x(1,4)+x(2,2)+x(2,3)+x(3,1)+x(3,2)>=20
    x(1,4)+x(2,3)+x(3,2)+x(4,1)>=12];
[sol,fval,flag,out]=solve(prob),sol.x

4.投资的收一个风险

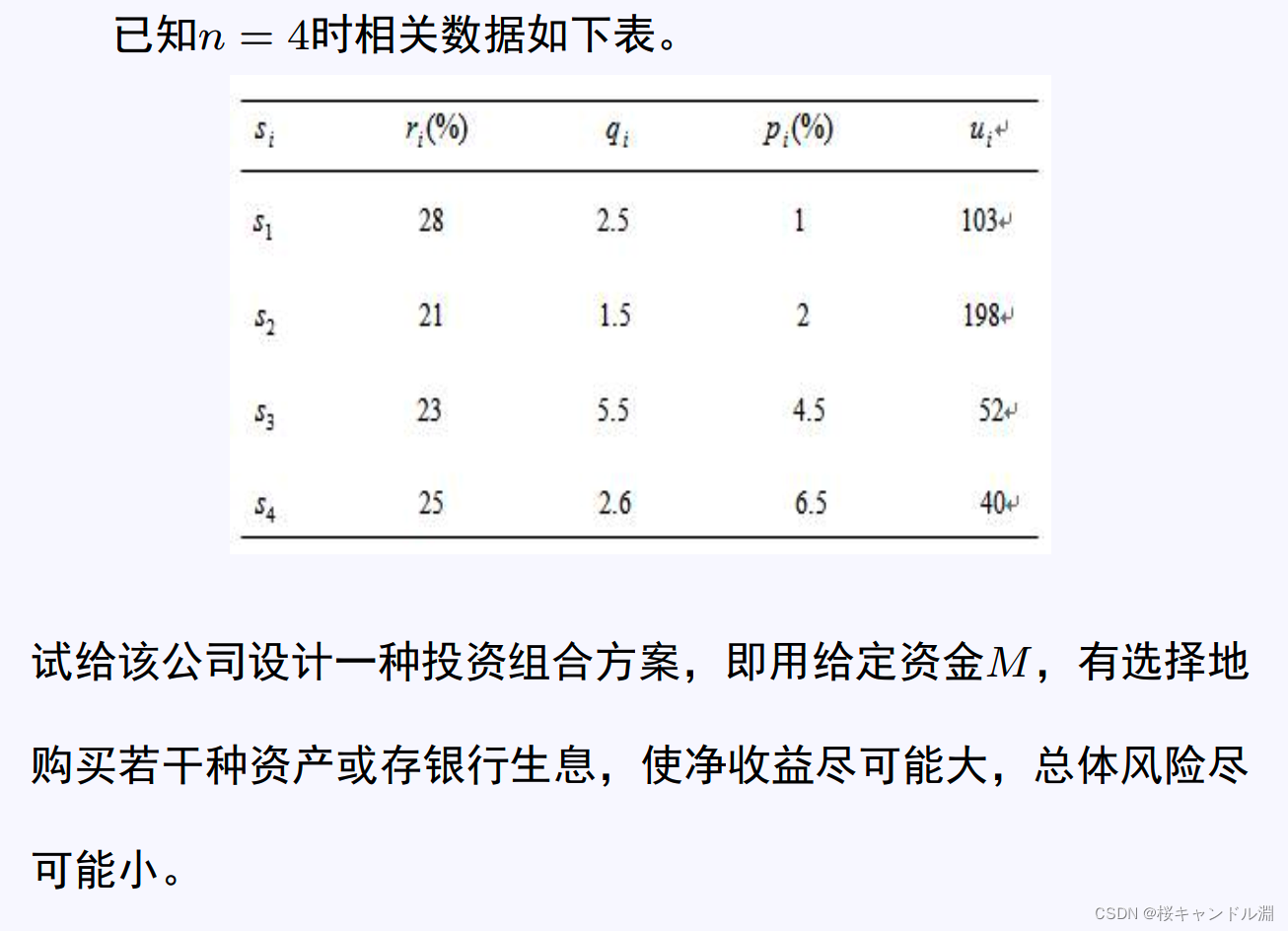
由于a是任意给定的风险度，我们可以从a=0开始，以步长△a=0.001进行循环搜索，编制程序

clear
a=0;
hold on
while a<0.05
    c=[-0.05,-0.27,-0.19,-0.185,-0.185];
    A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];
    b=a*ones(4,1);
    Aeq=[1,1.01,1.02,1.045,1.065];
    beq=1;
    LB=zeros(5,1);
    [x,Q]=linprog(c,A,b,Aeq,beq,LB);
    Q=-Q;
    plot(a,Q,'*r');
    a=a+0.001;
end  
 xlabel('a'),ylabel('Q')

clc,clear
prob=optimproblem('ObjectiveSense','max');
x=optimvar('x',5,1,'LowerBound',0);
c=[0.05,0.27,0.19,0.185,0.185];
Aeq=[1,1.01,1.02,1.045,1.065];
prob.Objective=c*x;M=10000;
prob.Constraints.con1=Aeq*x==M;
q=[0.025,0.015,0.055,0.026]';
a=0;aa=[];QQ=[];XX=[];hold on
while a<0.05
    prob.Constraints.con2=q.*x(2:end)<=a*M;
    [sol,Q,flag,out]=solve(prob);
    aa=[aa;a];QQ=[QQ;Q];
    XX=[XX;sol.x'];
    a=a+0.001;
end
plot(aa,QQ,'*k')
xlabel('a'),ylabel('Q')

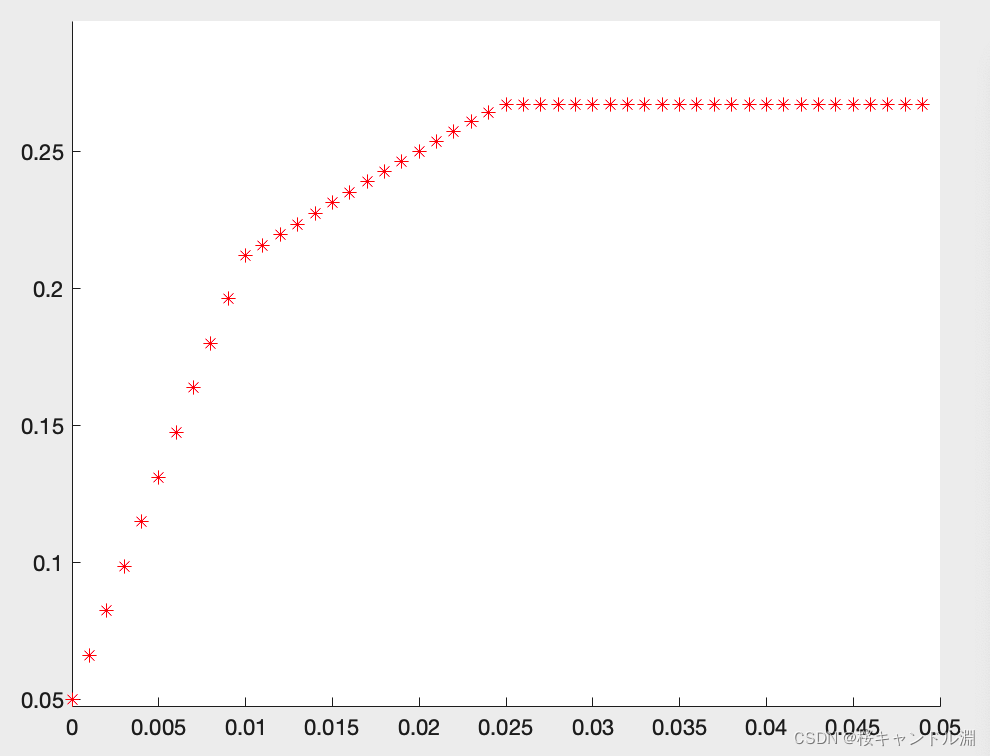
三、灵敏度分析（Lingo）

1.模板题

某家公司制造书桌，椅子和桌子，所用的资源有三种：木料、木工和漆工。生产数据如下表所示：

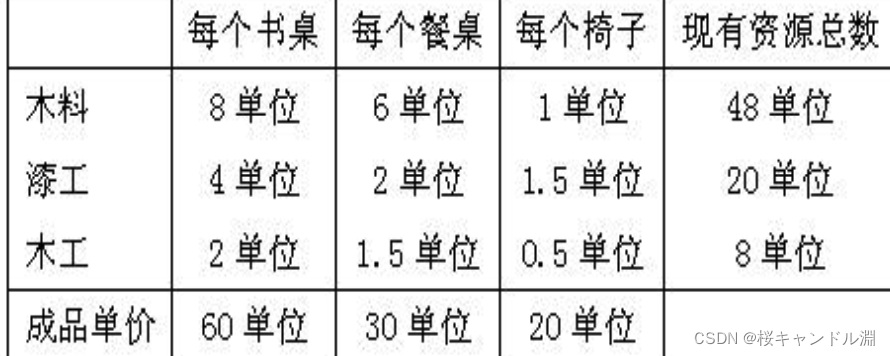
若要求桌子的生产量不超过5件，如何安排三种产品的生产可使利润最大？
使用DESK,TABLES和CHARIRS分别表示三种产品的生产量，建立LP模型

model:
max=60*desks+30*tables+20*chairs;
8*desks+6*tables+chairs<=48;
4*desks+2*tables+1.5*chairs<=20;
2*desks+1.5*tables+.5*chairs<=8;
tables<=5;
end

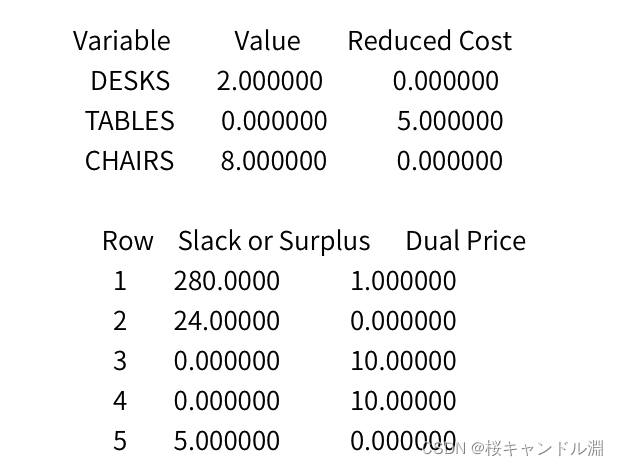
2.玩具公司生产玩具问题

某玩具公司分别生产三种新型玩具，每月可供应量分别为1000件，2000件，2000件，它们分别被送到甲、乙、丙三个百货商店销售。已知每月各百货商店各类玩具总和的预期销售量均为1500件，由于经营方面原因，各商店销售不同玩具的盈利额不同，见下表。又知道丙百货商店要求至少供应C玩具1000件，而拒绝进A玩具。求满足上述条件下使总盈利额为最大的供销分配方案。

甲	乙	丙	可供应量
A	5	4	–
B	16	8	9
C	12	10	11

model:
sets:
places/1,2,3/:store;
toy/A,B,C/:supply;
matrix(places,toy):money,x;
endsets
data:
supply=1000 2000 2000;
money=5 4 0
16 8 9
12 10 11;
enddata
max=@sum(matrix:money*x);
@for(places(i):@sum(toy(j):x(i,j))<=supply(i));
@for(places(j):@sum(toy(i):x(i,j))<=1500);
x(3,3)>=1000;
x(1,3)=0;

四、运输问题（Lingo）

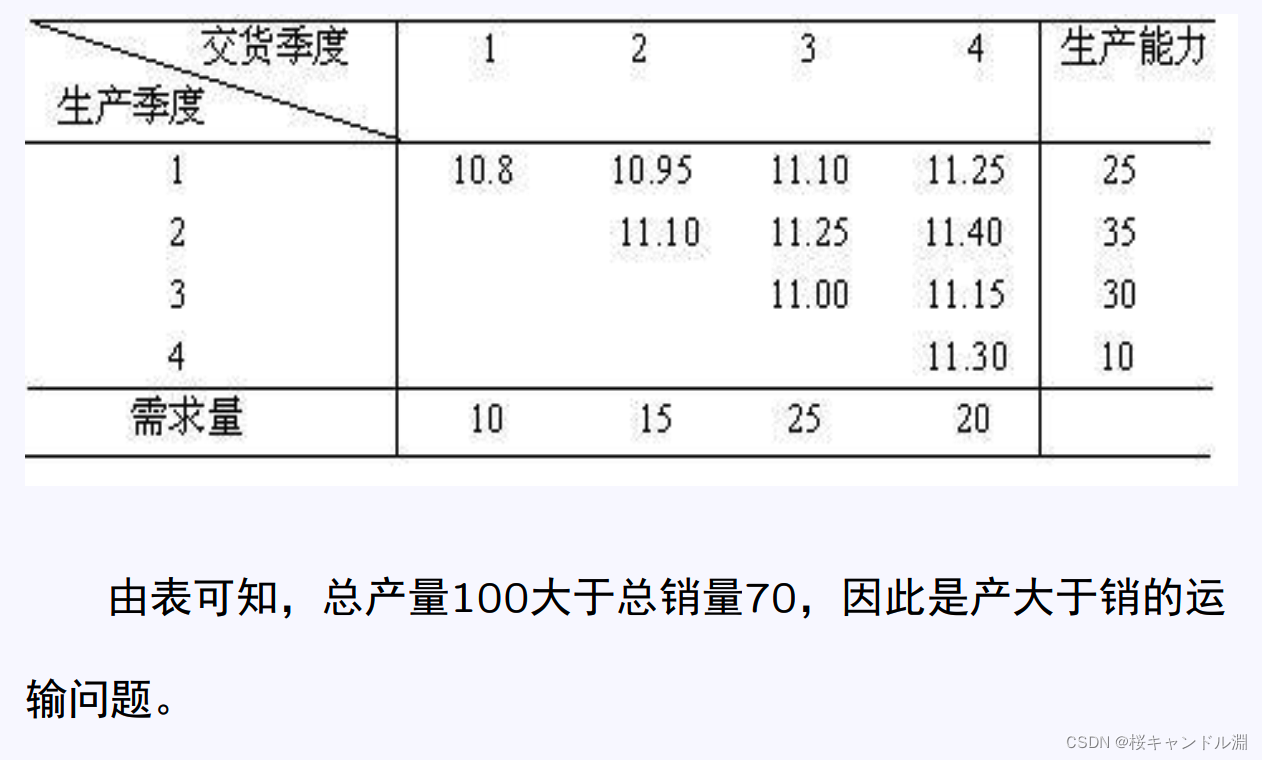
model:
sets:
warehouses/1..4/:a;
vendors/1..4/:b;
links(warehouses,vendors):c,x;
endsets

min=@sum(links:c*x);
@for(warehouses(i):@sum(vendors(j):x(i,j))<=a(i));
@for(vendors(j):@sum(warehouses(i):x(i,j))=b(j));
@for(links(i,j)|i#gt# j:x(i,j)=0);

data:
a=25 35 30 10;
b=10 15 25 20;
c=10.8 10.95 11.1 11.25
0 11.1 11.25 11.4
0 0 11 11.15
0 0 0 11.3;
enddata
end

五、整数规划问题（Lingo）

1.修建工厂问题

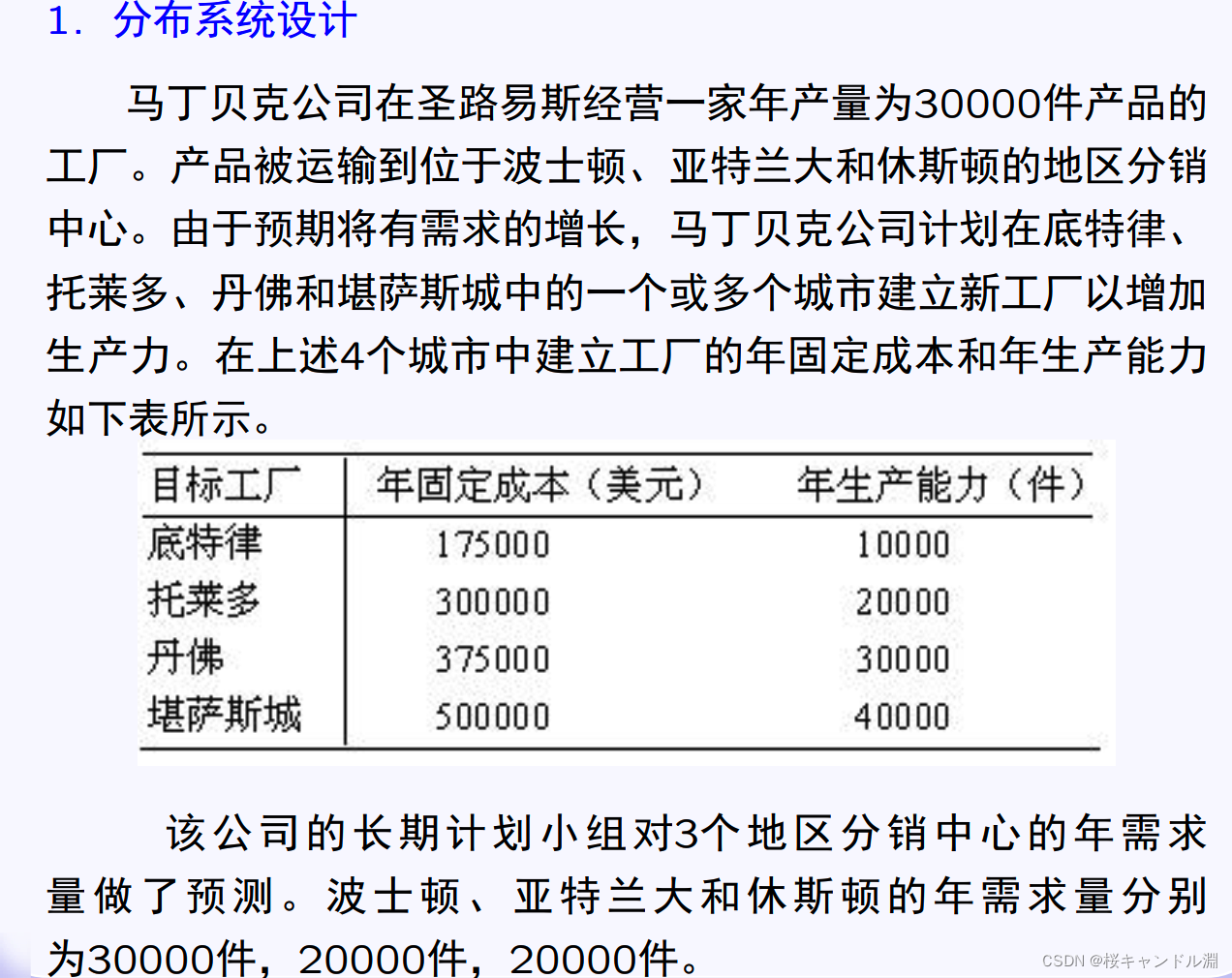
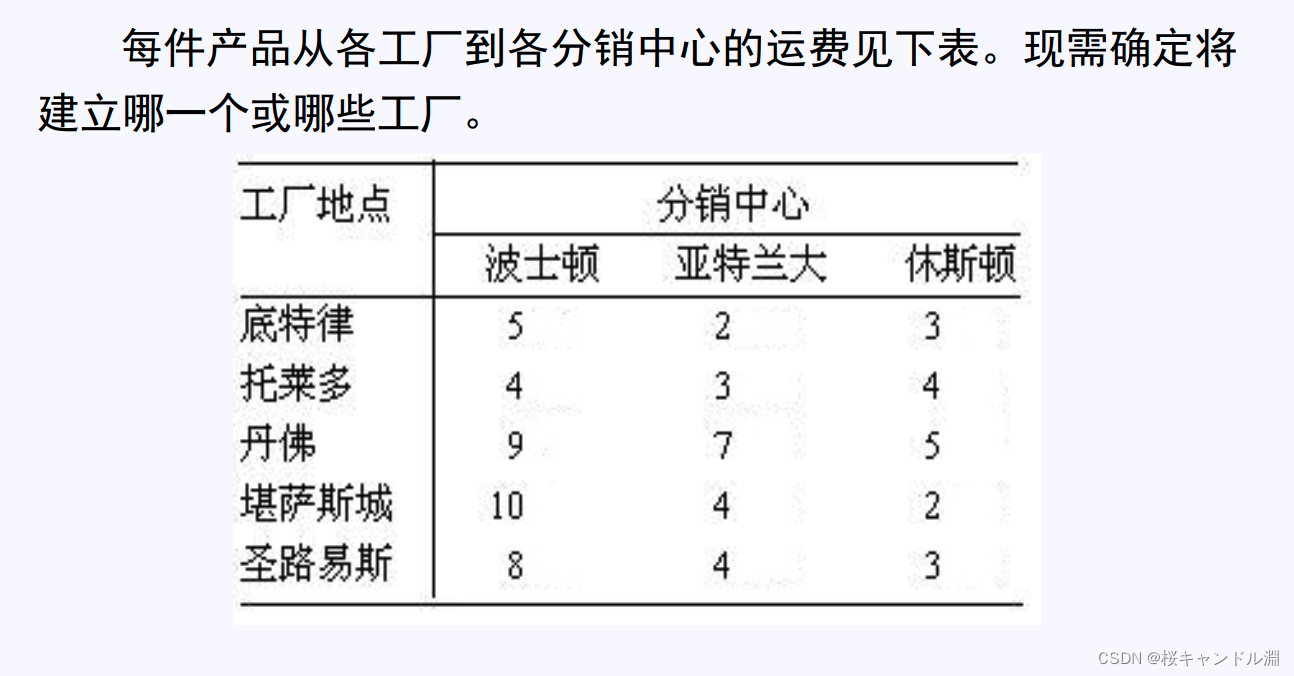
model:
sets:
warehouses/1..5/:cost,capacity,y;
vendors/1..3/:need;
links(warehouses,vendors):c,x;
endsets

min=@sum(links(i,j):c(i,j)*x(i,j))+@sum(warehouses(i):cost(i)*y(i));
@for(warehouses(i):@sum(vendors(j):x(i,j))<=capacity(i)*y(i));
@for(warehouses:@bin(y));
y(5)=1;

data:
cost=175000,300000,375000,500000,0;
capacity=10000,20000,30000,40000,30000;
need=30000,20000,20000;
c=5 2 3
4 3 4
9 7 5
10 4 2
8 4 3;
enddata

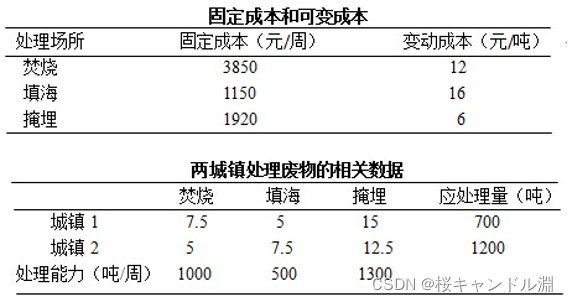
2.垃圾处理问题

某地区有两个镇，它们每周分别产生700吨和1200吨固体废物。现拟用三种方式（焚烧、填海、掩埋）分别在三个场地对这些废物进行处理。每个场所的处理成本分为固定成本和可变成本两部分，其数据见表1。两城镇至各处理场所的运输成本、应处理量与各处理场所的能力如表2所示。试求使两城镇处理固体废物总费用最小的方案。

model:
sets:
!固定成本,可变成本,容量;
cost/1,2,3/:stable_cost,unstable_cost,capacity,y;
!需要处理的吨数;
need/1,2/:need_ton;
!运输成本;
links(cost,need):c,x;
endsets

data:
stable_cost=3850,1150,1920;
unstable_cost=12,16,6;
capacity=1000,500,1300;
need_ton=700,1200;
c=7.5 5
    5 7.5
   15 12.5;
enddata

!运输成本,加上固定成本,加上可变成本的最小值;
min=@sum(links(i,j):x(i,j)*c(i,j))+@sum(cost(i):stable_cost(i)*y(i))+@sum(cost(i):@sum(need(j):x(i,j))*unstable_cost(i));
!将y设置为0,1约束,表示用不用这种处理方法;
@for(cost:@bin(y));
!每一种处理方式累加起来,小于最大能够处理的吨数;
@for(cost(i):@sum(need(j):x(i,j))<=capacity(i)*y(i));
!每一种处理方式累加起来等于需要处理的总吨数;
@for(need(j):@sum(cost(i):x(i,j))=need_ton(j));

六、最短路径问题（Lingo）

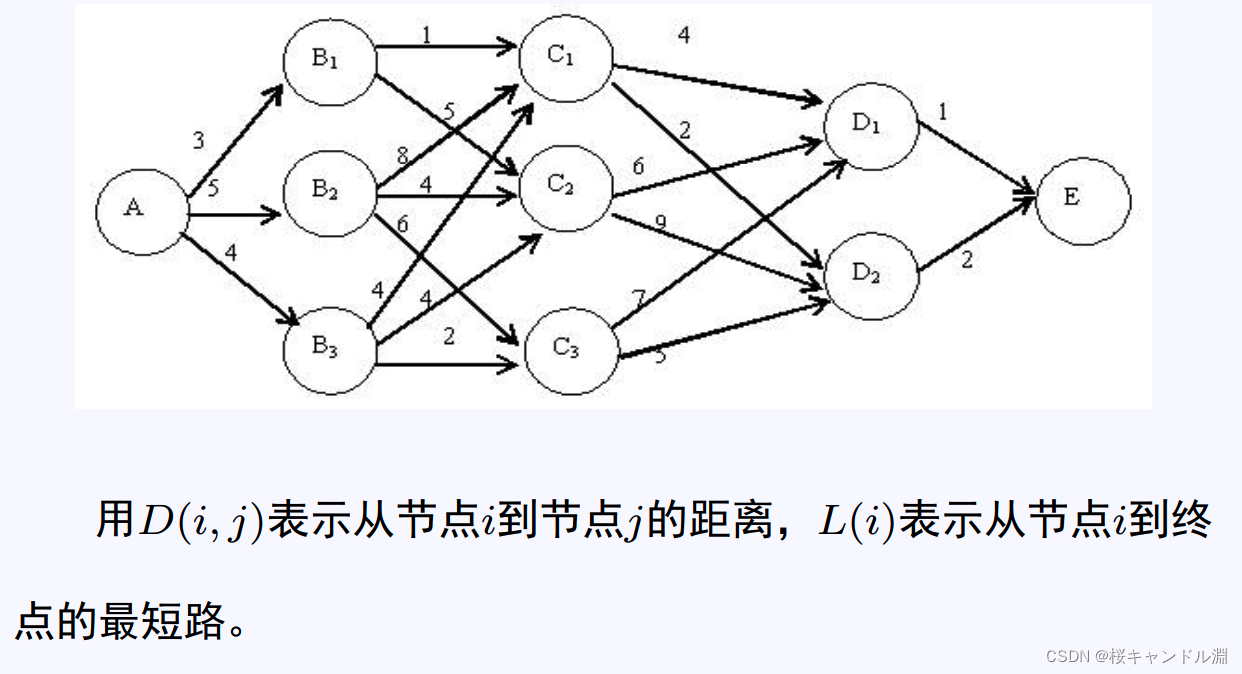
model:
sets:
nodes/A,B1,B2,B3,C1,C2,C3,D1,D2,E/:L;
arcs(nodes,nodes)/A,B1 A,B2 A,B3 B1,C1 B1,C2 B2,C1 B2,C2 B2,C3 B3,C1 B3,C2 B3,C3 C1,D1 C1,D2 C2,D1 C2,D2 C3,D1 C3,D2 D1,E D2,E/:D,F;
endsets

data:
D=3 5 4 1 5 8 4 6 4 4 2 4 2 6 9 7 5 1 2;
enddata

L(10)=0;!边界条件;
@for(nodes(i)|i#lt# @size(nodes):L(i)=@min(arcs(i,j):D(i,j)+L(j)));!递推方程;
@for(arcs(i,j):F(i,j)=@if(L(i)#eq# D(i,j)+L(j),1,0));!判断弧是否在最短路径上，便于确定最短路线;
end

七、网络最优化问题（Lingo）

1.最小费用问题

model:
sets:
nodes/f1,f2,dc,w1,w2/:d;
arcs(nodes,nodes)/f1,w1 f1,dc f2,w2 f2,dc dc ,w1 dc,w2/:cap,cost,flow;
endsets

data:
d=80 70 0 -60 -90;
cap=200 50 200 50 50 50;
cost=700 300 900 400 200 400;
enddata

min=@sum(arcs:cost*flow);
@for(nodes(i):@sum(arcs(i,j):flow(i,j))-@sum(arcs(j,i):flow(j,i))=d(i));
@for(arcs:@bnd(0,flow,cap));

end

2.最大流问题

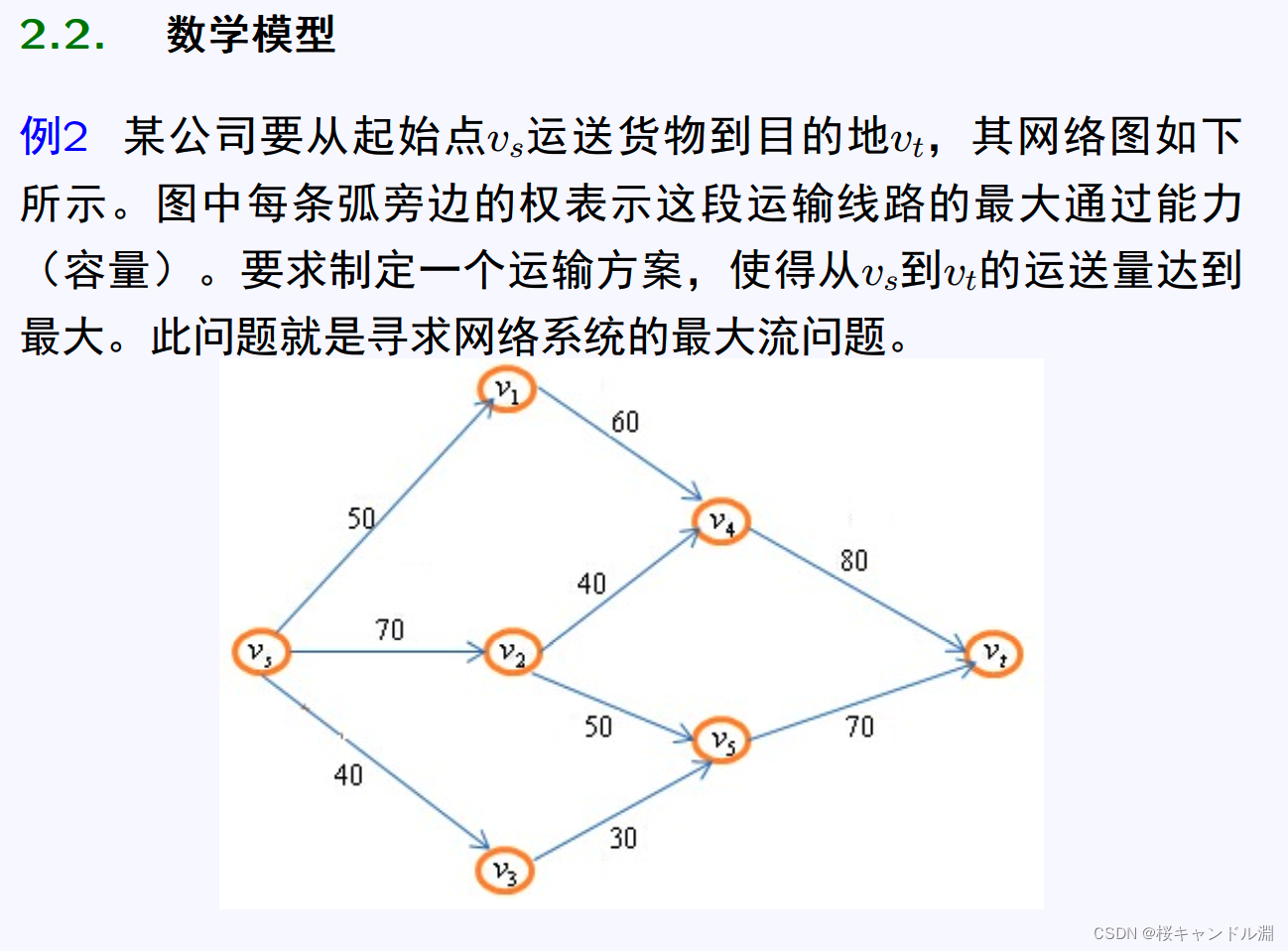
model:
sets:
nodes/s,1,2,3,4,5,t/;
arcs(nodes,nodes)/s,1 s,2 s,3 1,4 2,4 2,5 3,5 4,t 5,t/:cap,flow;
endsets

data:
cap=50 70 40 60 40 50 30 80 70;
enddata

max=mflow;
mflow=@sum(arcs(i,j)|i#eq#1:flow(i,j));
@for(nodes(i)|i#ne#1 #and# i#ne# @size(nodes):
    @sum(arcs(i,j):flow(i,j))-@sum(arcs(j,i):flow(j,i))=0);
@for(arcs:@bnd(0,flow,cap));
end

2.5最大流变形问题（多个收发点）

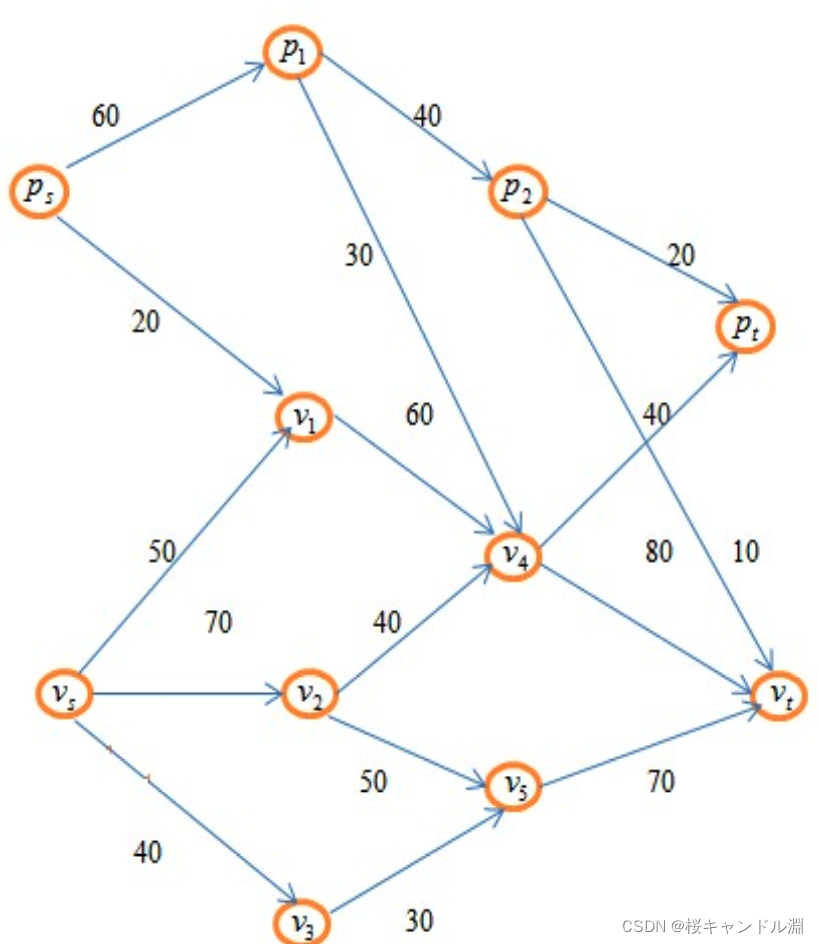
model:
sets:
nodes/ps,vs,p1,p2,v1,v2,v3,v4,v5,pt,vt/:;
arcs(nodes,nodes)/ps,p1 ps,v1 vs,v1 vs,v2 vs,v3 p1,p2 p1,v4 p2, pt p2,vt v1,v4 v2,v4 v2,v5 v3,v5 v4,pt v4,vt v5,vt/:cap,flow;
endsets
data:
cap=60 20 50 70 40 40 30 20 40 60 40 50 30 40 80 70;
enddata
max=mflow;
mflow=@sum(arcs(i,j)|i#le#2 :flow(i,j));
@for(nodes(i)|i#ne#1 #and# i#ne#2 #and# i#ne# @size(nodes)#and# i#ne# @size(nodes)-1:
    @sum(arcs(i,j):flow(i,j))-@sum(arcs(j,i):flow(j,i))=0);
@for(arcs:@bnd(0,flow,cap));
end

2.6最小费用最大流问题

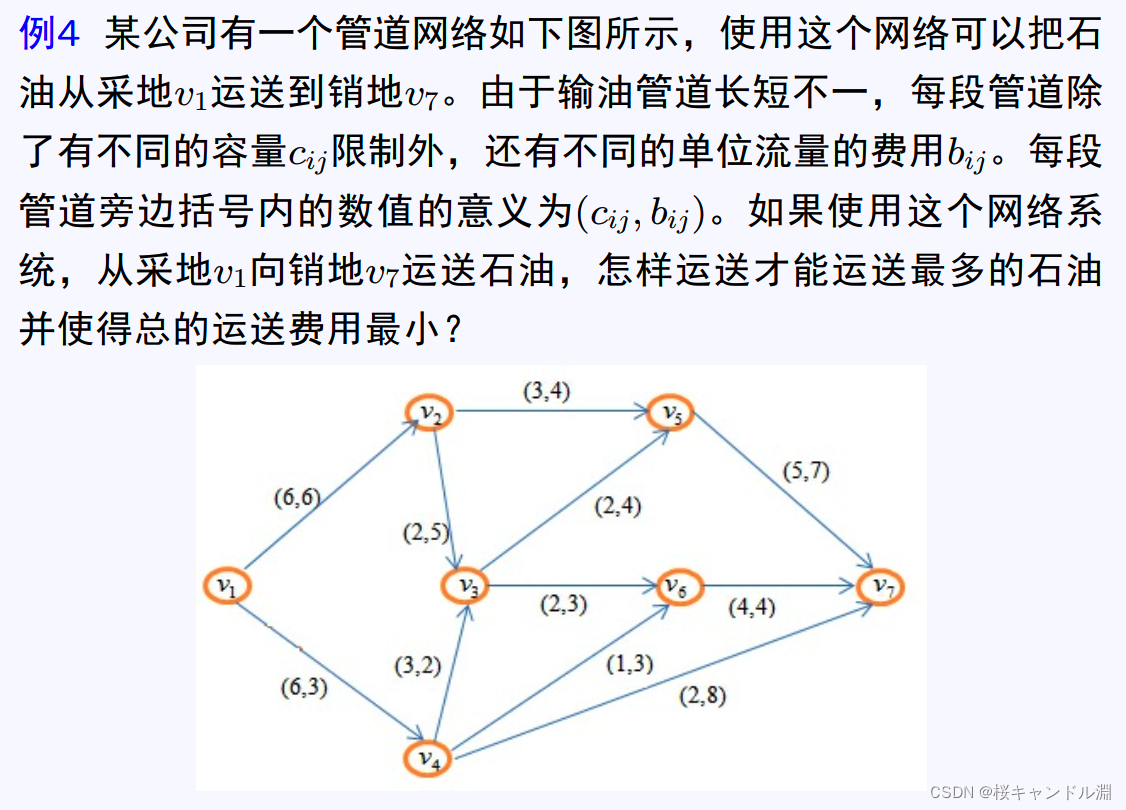
model:
sets:
nodes/1..7/:;
arcs(nodes,nodes)/1,2 1,4 2,3 2,5 3,5 3, 6 4,3 4,6 4, 7 5, 7 6, 7/:cap,flow;
endsets
data:
cap=6 6 2 3 2 2 3 1 2 5 4;
enddata
max=mflow;
mflow=@sum(arcs(i,j)|i#eq#1:flow(i,j));
@for(nodes(i)|i#ne#1 #and# i#ne# @size(nodes):
	@sum(arcs(i,j):flow(i,j))-@sum(arcs(j,i):flow(j,i))=0);
@for(arcs:@bnd(0,flow,cap));
end

model:
sets:
nodes/1..7/:d;
arcs(nodes,nodes)/1,2 1,4 2,3 2,5 3,5 3, 6 4,3 4,6 4, 7 5, 7 6, 7/:cap,cost,flow;
endsets
data:
d=10 0 0 0 0 0 -10;
cap=6 6 2 3 2 2 3 1 2 5 4;
cost=6 3 5 4 4 3 2 3 8 7 4;
enddata
min=@sum(arcs:cost*flow);
mflow=@sum(arcs:cost*flow);
@for(nodes(i):@sum(arcs(i,j):flow(i,j))-@sum(arcs(j,i):flow(j,i))=d(i));
@for(arcs:@bnd(0,flow,cap));
end

3.最短路问题

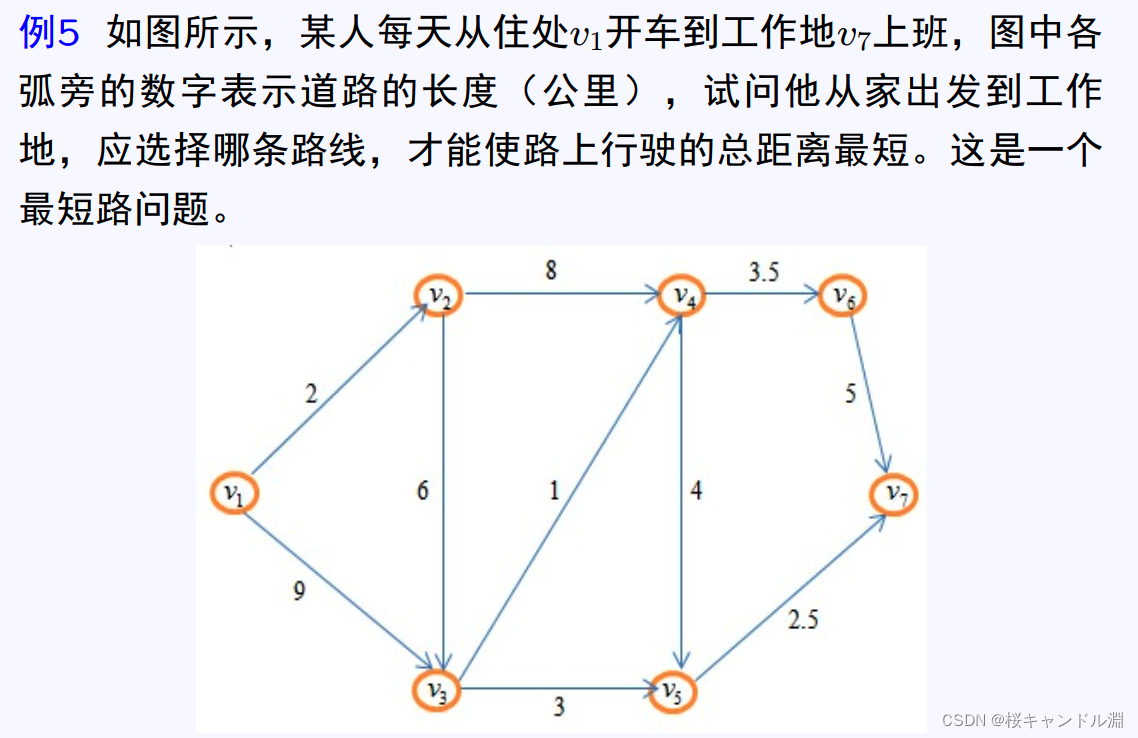
model:
sets:
nodes/1..7/:f;
arcs(nodes,nodes)/1,2 1,3 2,3 2,4 3,4 3,5 4,5 4,6 5,7 6,7/:d,x;
endsets
data:
f=1 0 0 0 0 0 -1;
d=2 9 6 8 1 3 4 3.5 2.5 5;
enddata
min=@sum(arcs:d*x);
@for(nodes(i):@sum(arcs(i,j):x(i,j))-@sum(arcs(j,i):x(j,i))=f(i));
end

4.网络运输问题

某公司是一个生产产品和在其零售渠道中销售产品的完全一体化的公司。产品生产后存放在公司的两个仓库中，直到零售渠道需要供应为止。公司用卡车把产品从两个工厂运送到仓库里，然后再把产品从仓库运送到零售渠道中。
以满载数量为单位，表1给出了每个工厂每月的产出，从工厂运送到仓库的单位运输成本以及每月从工厂运送到仓库的最大数量。
表1 从工厂运送到仓库的有关数据

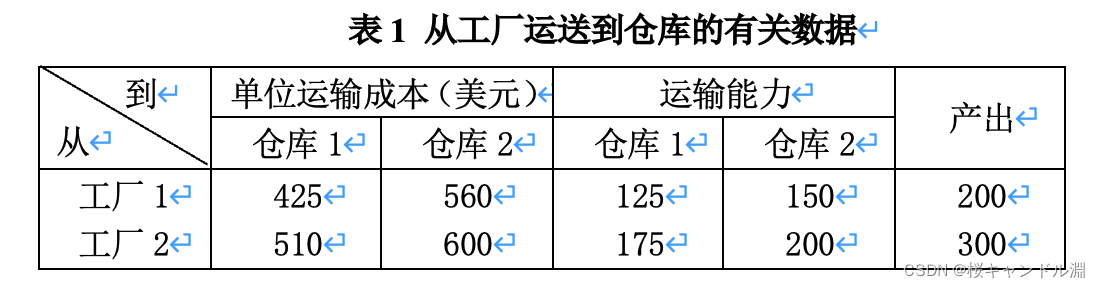
对于每一个零售点（RO），表2给出了它的月需求、从每个仓库到零售点的卡车单位运输成本以及每月从仓库运送到零售点的最大数量。
表2 从仓库运送到零售店的有关数据

管理层现在需要确定一个配送方案（每个月从每个工厂运送到每个仓库以及从每个仓库运送到每个零售渠道的满载车次数），使得总运输成本最小。
1．画一个网络图，描述该公司的配送网络。确定网络图中的供应点、转运点和需求点。

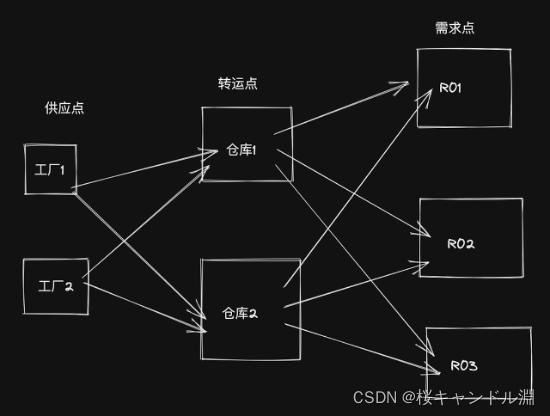
2.通过该配送网络，配送方案中最经济的总运输成本是多少？
总成本为488125元

model:
sets:
nodes/f1,f2,t1,t2,R01,R02,R03/:d;
arcs(nodes,nodes)/f1,t1 f1,t2 f2,t1 f2,t2 t1,R01 t1,R02 t1,R03 t2,R01 t2,R02 t2,R03/:cap,cost,flow;
endsets
data:
!输出-输入;
d=200 300 0 0 -150 -200 -150;
cap=125 150 175 200 100 150 100 125 150 75;
cost=425 560 510 600 470 505 490 390 410 440;
enddata
min=@sum(arcs:cost*flow);
@for(nodes(i) :@sum(arcs(i,j):flow(i,j))-@sum(arcs(j,i):flow(j,i))=d(i));
@for(arcs:@bnd(0,flow,cap));
End

3.该配送网络中，从工厂到零售渠道，哪条线路最为经济？成本是多少？（最短路问题，可以引入一个虚拟起点和一个虚拟终点）。
从工厂1到仓库1，再从仓库1到R01销售点是最经济的选择，成本是895元

model:
sets:
nodes/start,f1,f2,t1,t2,R01,R02,R03,end1/:d;
arcs(nodes,nodes)/start,f1 start,f2 f1,t1 f1,t2 f2,t1 f2,t2 t1,R01 t1,R02 t1,R03 t2,R01 t2,R02 t2,R03 R01,end1 R02,end1 R03,end1/:cost,flow;
endsets
data:
!输出-输入;
d=1 0 0 0 0 0 0 0 -1;
cost=0 0 425 560 510 600 470 505 490 390 410 440 0 0 0;
enddata
min=@sum(arcs:cost*flow);
@for(nodes(i) :@sum(arcs(i,j):flow(i,j))-@sum(arcs(j,i):flow(j,i))=d(i));
end

八、图论（Matlab）

最短路问题

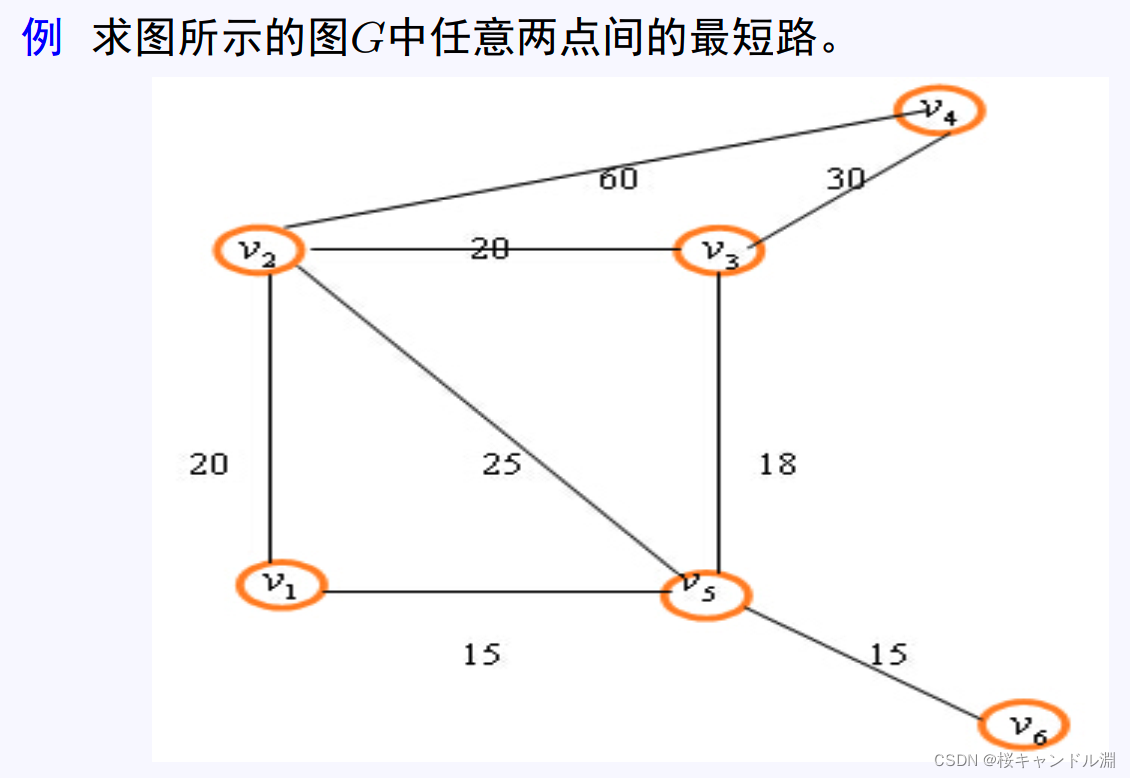
1.迪杰斯特拉算法

function [mydistance,mypath] = mydijkstra(a,sb,db)
%输入：a-邻接矩阵，sb-起点标号，db-终点标号
%输出：mydistance-最短路距离，mypath-最短路路径
n=size(a,1);visited(1:n)=0;
distance(1:n)=inf;  %保存起点到各顶点的最短距离
distance(sb)=0;parent(1:n)=0;
for i=1:n-1
    temp=distance;
    id1=find(visited==1); %查找已经标号的点
    temp(id1)=inf;        %已标号的点距离换成无穷
    [t,u]=min(temp);      %找标号值最小的顶点,t为距离，u为顶点标号
    visited(u)=1;         %标记已经标号的顶点
    id2=find(visited==0);  %查找未标号的顶点
    for v=id2
        if distance(u)+a(u,v)<distance(v)
           distance(v)=distance(u)+a(u,v); %修改标号值
           parent(v)=u;
        end
    end
end
mypath=[];
if parent(db)~=0  %如果存在路
    t=db;mypath=[db];
    while t~=sb
        p=parent(t);
        mypath=[p mypath];
        t=p;
    end
end
mydistance=distance(db);
return
      
end

% %利用dijkstra算法求任意两点的最短路;
% a=[0 20 inf inf 15 inf;20 0 20 60 25 inf;inf 20 0 30 18 inf;inf 60 30 0 inf inf;15 25 18 inf 0 15;inf inf inf inf 15 0];
% n=size(a,1);
% for i=1:6
%     for j=1:6
%         distance(i,j)=mydijkstra(a,i,j);
%     end
% end

主程序

%利用dijkstra算法解决选址问题;
a=[0 20 inf inf 15 inf;20 0 20 60 25 inf;inf 20 0 30 18 inf;inf 60 30 0 inf inf;15 25 18 inf 0 15;inf inf inf inf 15 0];
n=size(a,1);
for i=1:6
    for j=1:6
        distance(i,j)=mydijkstra(a,i,j);
    end
end
for i=1:6
    mindistance(i)=max(distance(i,:));
end
[d,u]=min(mindistance)

2.弗洛伊德算法

function [dist,mypath] = myfloyd(a,sb,db)
%输入：a-邻接矩阵，sb-起点标号，db-终点标号
%输出：dist-最短路距离，mypath-最短路路径
%a=[0 20 inf inf 15 inf;20 0 20 60 25 inf;inf 20 0 30 18 inf;inf 60 30 0 inf inf;15 25 18 inf 0 15;inf inf inf inf 15 0];
n=size(a,1);path=zeros(n);
for i=1:n
    for j=1:n
        if a(i,j)~=inf
            path(i,j)=j;  %j是i的后续点
        end
    end
end
for k=1:n
    for i=1:n
        for j=1:n
            if a(i,j)>a(i,k)+a(k,j)
                a(i,j)=a(i,k)+a(k,j);
                path(i,j)=path(i,k);
            end
        end
    end
end
dist=a(sb,db);
mypath=sb;t=sb;
while t~=db
    temp=path(t,db);
    mypath=[mypath,temp];
    t=temp;
end
return
      
end

主程序

%输出任意两点间的最短距离
a=[0 20 inf inf 15 inf;20 0 20 60 25 inf;inf 20 0 30 18 inf;inf 60 30 0 inf inf;15 25 18 inf 0 15;inf inf inf inf 15 0];
n=length(a);
for sb=1:n
    for db=1:n
        [dist1,mypath1] = myfloyd(a,sb,db);
        dist(sb,db)=dist1;
    end
end
dist