D - Neighbors (atcoder.jp)
(1)题意
给出M组关系,问是否有一个排列,能表示A[i]和B[i]相邻
(2)思路
考虑如果有环,显然不能满足排列,因为排列中度数最多为2,若有超过2的显然也不行。因此用并查集维护一下即可。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
struct DSU {
vector<int> f,siz;
int n;
DSU(int _n) {
n = _n;
f.resize(n + 1);
siz.resize(n + 1,1);
iota(f.begin(),f.end(),0);
}
inline int find(int x) {
if(x == f[x]) return x;
return f[x] = find(f[x]);
}
inline bool same(int x,int y) {
x = find(x),y = find(y);
return x == y;
}
inline void merge(int x,int y) {
if(same(x,y)) return ;
x = find(x),y = find(y);
siz[y] += siz[x];
f[x] = y;
}
//目前连通块个数
inline int connect() {
int res = 0;
for(int i = 1;i <= n;i ++) {
res += (i == find(i));
}
return res;
}
//求某一个联通块得大小
inline int count(int x) {
x = find(x);
return siz[x];
}
};
int deg[N];
void solve()
{
int n,m;
cin >> n >> m;
DSU dsu(n);
bool cycle = false;
rep(i,1,m) {
int u,v;
cin >> u >> v;
if(dsu.same(u,v)) {
cycle = true;
}
else {
dsu.merge(u,v);
deg[u] ++,deg[v] ++;
}
}
if(cycle) {
cout << "No" << '\n';
return;
}
rep(i,1,n) {
if(deg[i] > 2) {
cout << "No" << '\n';
return;
}
}
cout << "Yes" << '\n';
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T = 1;
// cin >> T;
while(T --) solve();
return 0;
}E - Minimal payments (atcoder.jp)
(1)题意
阿特科德王国使用的硬币有N种: A1日元、A2日元、……、AN日元硬币。
这里,1=A1<…<AN成立,且Ai+1是每一个1≤i≤N−1的Ai的倍数。
如果只用这些硬币支付一件价值X日元的商品,那么支付时使用的硬币和作为零钱退回的硬币的最少总数是多少?
当Y是一个至少为X的整数时,求正好表示Y日元所需的硬币数与正好表示Y−X日元所需的硬币数的最小和。
(2)思路
对于每一种支付,我们有两种决策,要么就是支付到最多的,然后剩下的用小币去凑,要么就是你多支付一张,小的就凑你多出来的那部分,因此直接记忆化dp即可。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
ll a[N];
map<ll,map<ll,ll>> dp;
const ll inf = 9e18;
inline ll dfs(ll X,int f)
{
if(f == 0 && X) return inf;
if(dp[X].count(f)) return dp[X][f];
ll r = X % a[f],p = X / a[f];
if(!r) return p;
return dp[X][f] = min(dfs(r,f - 1) + p,dfs(a[f] - r,f - 1) + p + 1);
}
void solve()
{
int n;
ll X;
cin >> n >> X;
rep(i,1,n) cin >> a[i];
cout << dfs(X,n);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T = 1;
// cin >> T;
while(T --) solve();
return 0;
}F - Jealous Two (atcoder.jp)
(1)题意
有一个长度为N的A数组,A[i]代表A对i这件物品的好感度,有一个长度为N的B数组,B[i]代表B对i这件物品的好感度,现在让你求有多少对[i,j]满足A[i] >= A[j]并且B[i] <= B[j]。
(2)思路
很明显这是一个二维偏序问题,我们直接sort+树状数组秒了(特殊处理一下重复的就行)。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 4e5 + 10;
vector<int> ver;
int a[N],b[N];
int get(int x)
{
return lower_bound(all(ver),x) - ver.begin() + 1;
}
PII z[N];
template <typename T>
struct Fenwick {
const int n;
std::vector<T> a;
Fenwick (int n) : n(n), a(n + 1) {}
void clear() {
for(int i = 1;i <= n;i ++) {
a[i] = 0;
}
}
void add(int pos, T x) {
for (int i = pos; i <= n; i += i & -i) {
a[i] += x;
}
}
T query(int x) {
T res = 0;
for (int i = x; i; i -= i & -i) {
res += a[i];
}
return res;
}
T query(int l, int r) {
if (l == 0 || l > r) {
return 0;
}
return query(r) - query(l - 1);
}
//找到大于k得第一个地方
T kth(int k) {
int pos = 0;
for(int j = 31 - __builtin_clz(n);j >= 0;j --) {
if(pos + (1 << j) <= n && k > a[pos + (1 << j)]) {
pos += 1 << j;
k -= a[pos];
}
}
return pos + 1;
}
};
//使用Fenwick<ll> fen(n)
void solve()
{
int n;
cin >> n;
rep(i,1,n) {
cin >> a[i];
ver.pb(a[i]);
}
rep(i,1,n) {
cin >> b[i];
ver.pb(b[i]);
}
sort(all(ver));
ll Ans = 0;
map<pair<int,int>,int> cnt;
rep(i,1,n) {
a[i] = get(a[i]);
b[i] = get(b[i]);
z[i] = {a[i],-b[i]};
cnt[z[i]] ++;
}
for(auto [x,y]: cnt) Ans += 1ll * y * (y - 1) / 2;
sort(z + 1,z + 1 + n);
Fenwick<int> fen(400000);
rep(i,1,n) {
fen.add(-z[i].se,1);
Ans += i - fen.query(-z[i].se - 1);
}
cout << Ans;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T = 1;
// cin >> T;
while(T --) solve();
return 0;
}H - Minimum Coloring (atcoder.jp)
(1)题意
我们有一个行数为H,列数为W的网格。让 (i,j)表示从上往下第i行和从左往下第j列的正方形。在这个网格上有N个白色棋子,编号为1到N。棋子i在(Ai,Bi)上。你可以支付Ci的费用将棋子i变成黑棋,求每行每列至少有一颗黑子所需的最小总费用。
(2)思路
很显然的一个列拆点,把行向列连边的费用流,不过这题特殊的是必须行列都有,我们考虑如下建图。
把每一行当作一个节点,从S->i流M的流量,从i->P流m-1的流量,从p向每一列流n-1的流量,从列向t流n的流量,最后给点的边的[u,v]的价值w 相当于从u->(v + n)流1的流量费用为w,最后跑费用流即可。因为题目保证会出现每行每列至少出现一个,因此一定会把n*m的流量流满。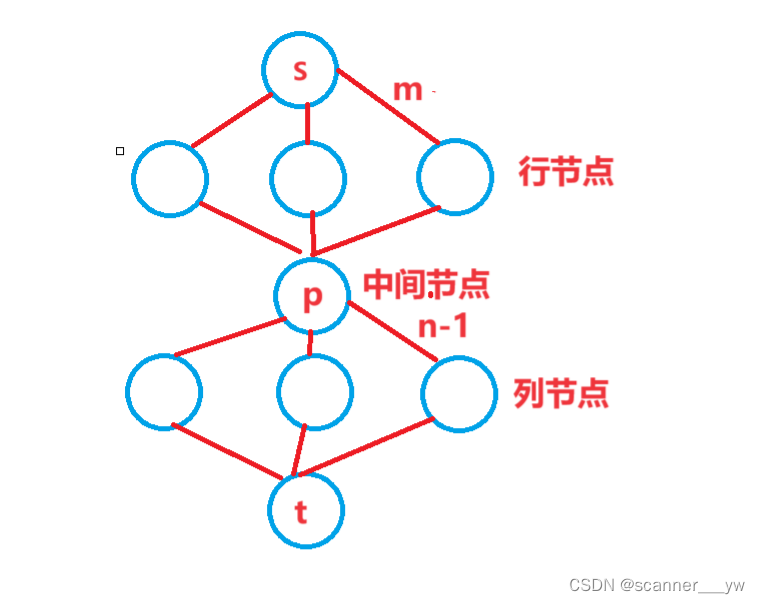
(3)代码
#include <bits/stdc++.h>
#define rep(i, a, b) for (int i = a; i < (b); ++i)
#define all(x) begin(x), end(x)
#define sz(x) (int)(x).size()
#define uniq(x) x.resize(unique(all(x)) - x.begin())
#define ff first
#define ss second
#define pb push_back
#define emb emplace_back
using namespace std;
using ull = unsigned long long;
using ll = long long;
using pii = pair<int, int>;
using vi = vector<int>;
template <typename T>
using min_heap = priority_queue<T, vector<T>, greater<T>>;
#define RN 100005
struct SimplexMinCostMaxFlow {
using Flow = ll;
using Cost = ll;
struct Network {
int nxt, to;
Flow cap;
Cost cost;
};
Network net_pool[RN * 2];
int ncnt = 1;
#define nnode(x) net_pool[x]
#define nnxt(x) nnode(x).nxt
#define nto(x) nnode(x).to
#define ncap(x) nnode(x).cap
#define ncost(x) nnode(x).cost
int head[RN], fa[RN], fe[RN], pi[RN], mark[RN], cyc[RN], ti;
inline void addEdge(int u, int v, Flow cap, Cost cost) {
nnode(++ncnt) = (Network){head[u], v, cap, cost};
head[u] = ncnt;
nnode(++ncnt) = (Network){head[v], u, 0, -cost};
head[v] = ncnt;
}
void initTree(int x) {
mark[x] = 1;
for (int i = head[x]; i; i = nnxt(i)) {
int v = nto(i);
if (!mark[v] && ncap(i)) {
fa[v] = x, fe[v] = i;
initTree(v);
}
}
}
int phi(int x) {
if (mark[x] == ti) return pi[x];
return mark[x] = ti, pi[x] = phi(fa[x]) - ncost(fe[x]);
}
void pushFlow(int e, Cost &cost) {
int pen = nto(e ^ 1), lca = nto(e);
ti++;
while (pen) mark[pen] = ti, pen = fa[pen];
while (mark[lca] != ti) mark[lca] = ti, lca = fa[lca];
int e2 = 0, f = ncap(e), path = 2, clen = 0;
for (int i = nto(e ^ 1); i != lca; i = fa[i]) {
cyc[++clen] = fe[i];
if (ncap(fe[i]) < f) f = ncap(fe[e2 = i] ^ (path = 0));
}
for (int i = nto(e); i != lca; i = fa[i]) {
cyc[++clen] = fe[i] ^ 1;
if (ncap(fe[i] ^ 1) <= f) f = ncap(fe[e2 = i] ^ (path = 1));
}
cyc[++clen] = e;
for (int i = 1; i <= clen; i++) {
ncap(cyc[i]) -= f, ncap(cyc[i] ^ 1) += f;
cost += 1ll * ncost(cyc[i]) * f;
}
if (path == 2) return;
int laste = e ^ path, last = nto(laste), cur = nto(laste ^ 1);
while (last != e2) {
mark[cur]--;
laste ^= 1;
swap(laste, fe[cur]);
swap(last, fa[cur]);
swap(last, cur);
}
}
pair<Flow, Cost> maxflow(int s, int t) {
int lhead = head[s], lhead2 = head[t];
addEdge(t, s, 0x7fffffffff, -0x7f7f7f7f);
initTree(t);
mark[t] = ti = 2, fa[t] = 0;
Cost cost = 0;
for (int i = 2, pre = ncnt; i != pre; i = i == ncnt ? 2 : i + 1) {
if (ncap(i) && ncost(i) < phi(nto(i ^ 1)) - phi(nto(i)))
pushFlow(pre = i, cost);
}
head[s] = lhead, head[t] = lhead2, ncnt -= 2;
Flow flow = ncap(ncnt + 2);
cost += 1ll * flow * 0x7f7f7f7f;
return {flow, cost};
}
};
SimplexMinCostMaxFlow flow;
int main() {
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int n, m, q;
int s, t, p;
cin >> n >> m >> q;
s = n + m + 1,p = n + m + 2,t = n + m + 3;
for(int i = 1;i <= n;i ++) {
flow.addEdge(s,i,m,0);
flow.addEdge(i,p,m - 1,0);
}
for(int i = 1;i <= m;i ++) {
flow.addEdge(i + n,t,n,0);
flow.addEdge(p,i + n,n - 1,0);
}
for(int i = 1;i <= q;i ++) {
int x,y,z;
cin >> x >> y >> z;
flow.addEdge(x,y + n,1,z);
}
cout << flow.maxflow(s,t).second;
// cout << ans.second << '\n';
return 0;
}