PyTorch实例：简单线性回归的训练和反向传播解析

文章目录

🥦引言
🥦什么是反向传播？
🥦反向传播的实现（代码）
🥦反向传播在深度学习中的应用
🥦链式求导法则
🥦总结

🥦引言

在神经网络中，反向传播算法是一个关键的概念，它在训练神经网络中起着至关重要的作用。本文将深入探讨反向传播算法的原理、实现以及在深度学习中的应用。

🥦什么是反向传播？

反向传播（Backpropagation）是一种用于训练神经网络的监督学习算法。它的基本思想是通过不断调整神经网络中的权重和偏差，使其能够逐渐适应输入数据的特征，从而实现对复杂问题的建模和预测。

反向传播算法的核心思想是通过计算损失函数（Loss Function）的梯度来更新神经网络中的参数，以降低预测值与实际值之间的误差。这个过程涉及到两个关键步骤：前向传播（Forward Propagation）和反向传播。

前向传播（forward）：在前向传播过程中，输入数据通过神经网络，每一层都会进行一系列的线性变换和非线性激活函数的应用，最终得到一个预测值。这个预测值会与实际标签进行比较，得到损失函数的值。
反向传播（backward）：在反向传播过程中，我们计算损失函数相对于网络中每个参数的梯度。这个梯度告诉我们如何微调每个参数，以减小损失函数的值。梯度下降算法通常用于更新权重和偏差。

🥦反向传播的实现（代码）

要实现反向传播，我们需要选择一个损失函数，通常是均方误差（Mean Squared Error）或交叉熵（Cross-Entropy）。然后，我们计算损失函数相对于每个参数的偏导数（梯度）。这可以使用链式法则来完成，从输出层向后逐层传递。

接下来，我们使用梯度下降或其变种来更新权重和偏差。梯度下降的核心思想是沿着梯度的反方向调整参数，以降低损失函数的值。这个过程不断迭代，直到损失函数收敛到一个较小的值或达到一定的迭代次数。

在代码实现前，我能先了解一下反向传播是怎么个事，下文主要以图文的形式进行输出
这里我们回顾一下梯度，首先假设一个简单的线性模型
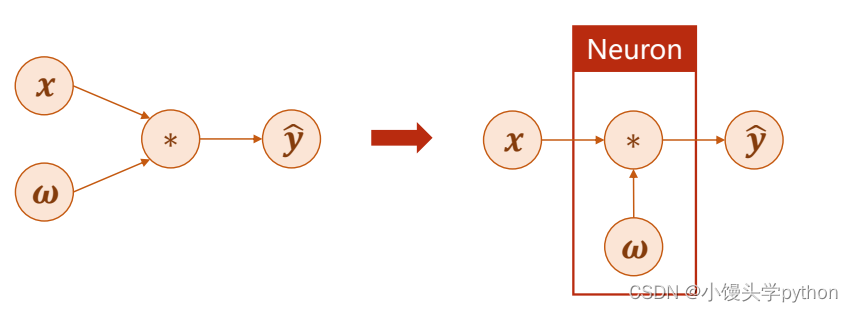
在这里插入图片描述
接下来，我们展示一下什么是前向传播（其实就是字面的意思），在神经网络中通常以右面的进行展示，大概意思就是输入x与权重w进行乘法运算，得到了y’

下图是随机梯度下降的核心公式以及损失函数的导数
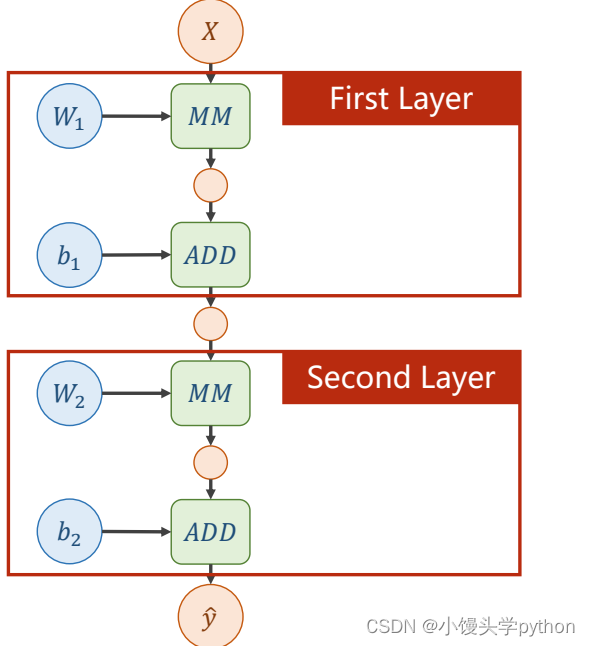
在这里插入图片描述
下图是一个两层的神经网络

如果以图画的形式理解可以从下图进行理解
首先还是和之前的一样，进行输入和权重的矩阵乘法（这里刘二大人推荐一个查询书籍MatrixCookbook）

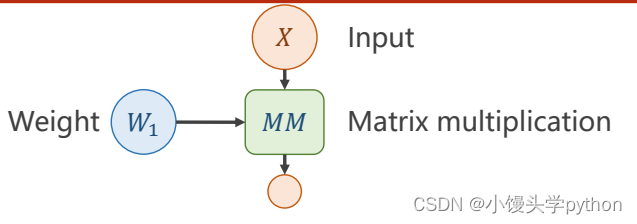
之后引入b，不理解的小伙伴可以当做截距
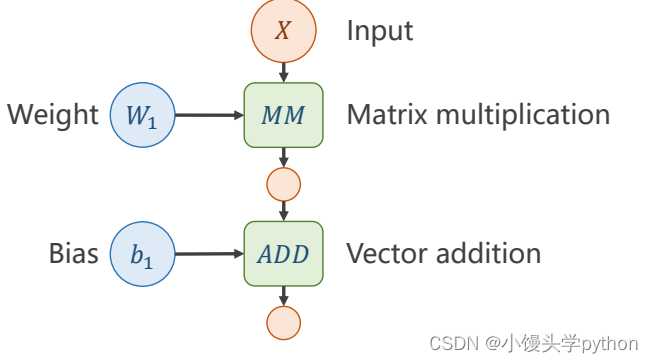
在这里插入图片描述
那么下图框框里面的就是一层神经网络

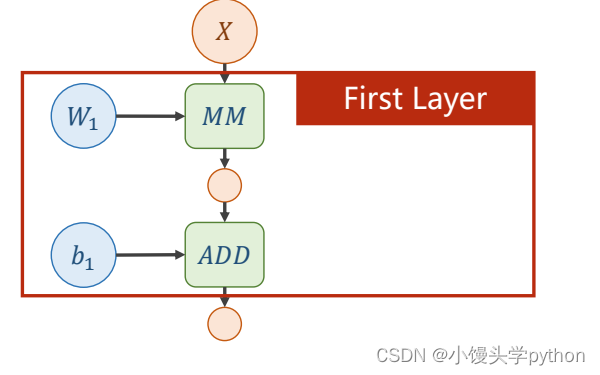
那么两层也就可以清晰的得到了，最后得到了y’

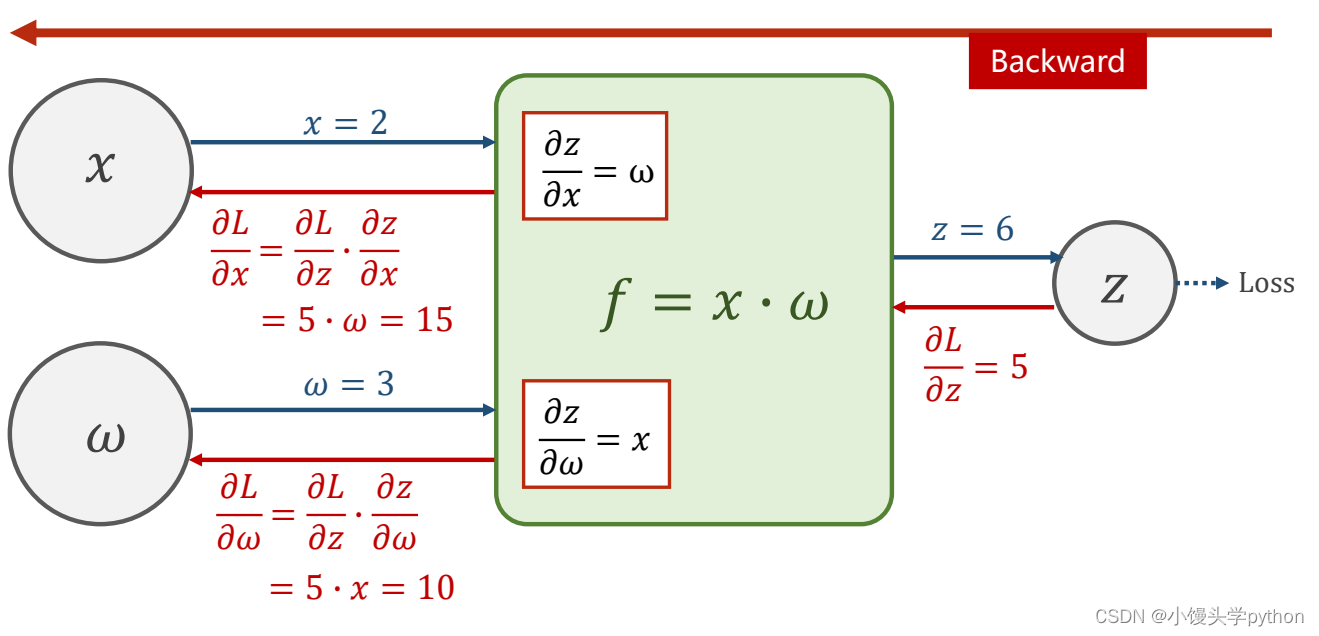
刚刚的描述过于笼统，接下来详细介绍一下前向和后向
在前向传播运算中，f里面进行了z对x和w的偏导求解
在这里插入图片描述
在反向传播里，损失loss对z的偏导，以及经过f后，求得loss对x和w的偏导。按理说我们只用权重w，但是如果x是上一层的输出（多层神经网络）那就需要了，至于loss对x和w的偏导怎么求参考结尾的链式求导法则
在这里插入图片描述

接下来我们可以假设x=2，w=3，手动的求解loss对x和w的偏导，求完就可以对权重的更新了
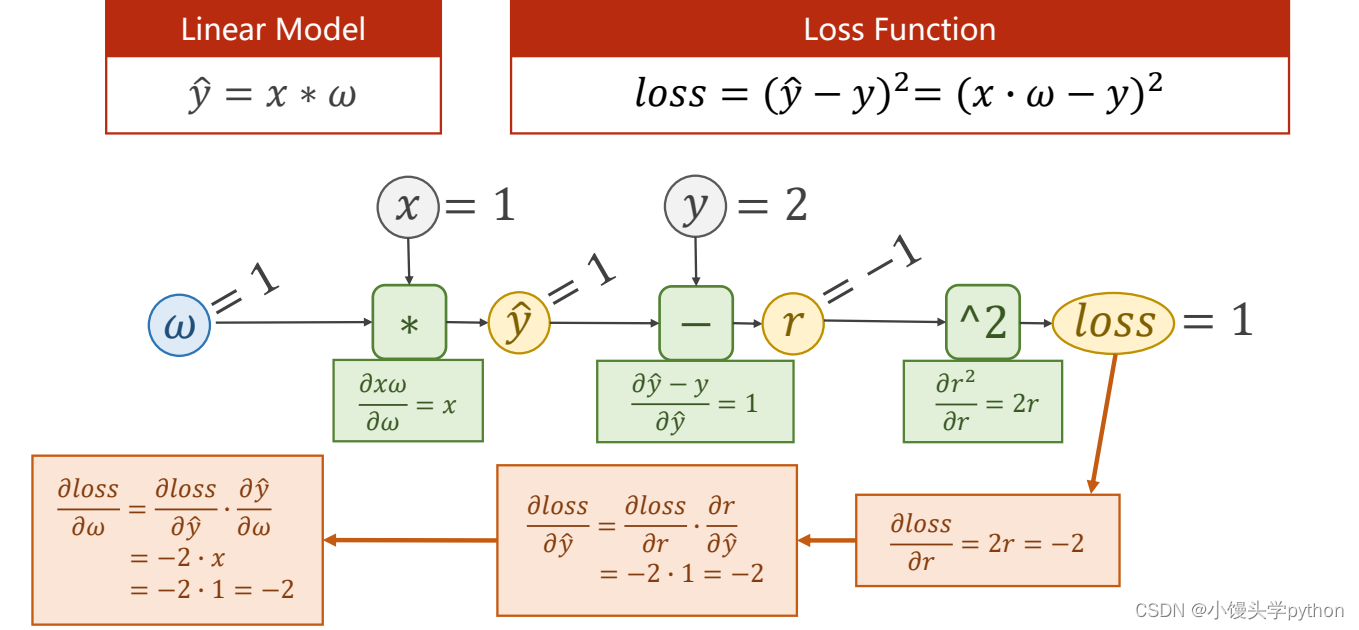
在这里插入图片描述
也可以从如下的计算图进行清晰的展示前后向传播

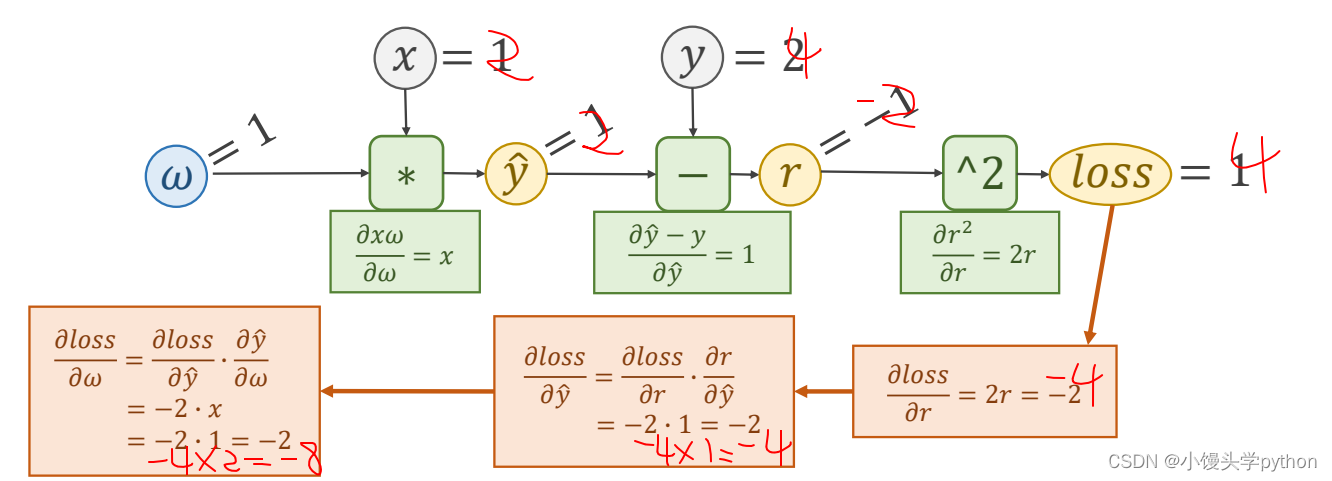
如果x=2，y=4，我写了一下如果错了欢迎指正

这里粗略的解释一下pytorch中的tensor，大概意思是它重要，其中还有包含了可以存储数值的data和存储梯度的grad
在这里插入图片描述

w.requires_grad = True # 默认是不自动计算梯度，需自行设计

如下是完整的代码（带注释）

import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = torch.Tensor([1.0])
w.requires_grad = True

def forward(x):
    return x * w # 这里的权重w是tensor
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

print("predict (before training)",  4, forward(4).item())
for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l = loss(x, y)  # 前向传播
        l.backward()  # 后向传播
        print('\tgrad:', x, y, w.grad.item())  # item是为了防止计算图
        w.data = w.data - 0.01 * w.grad.data  # 注意不要直接取grad，因为这也属于重新创建计算图，只要值就好
        w.grad.data.zero_()  # 注意要清零否者会造成loss对w的导数一直累加，下图说明
    print("progress:", epoch, l.item())
print("predict (after training)", 4, forward(4).item())

循环进行模型训练，这里设置了100个训练周期（epochs）。
在每个周期内，遍历输入数据 x_data 和对应的目标数据 y_data。
对于每个数据点，计算前向传播，然后进行反向传播以计算梯度。
打印出每次反向传播后权重 w 的梯度值。
更新权重 w，使用梯度下降法更新参数，以最小化损失函数。
在更新权重之前，使用 .grad.data.zero_() 来清零梯度，以防止梯度累积。
.item() 的作用是将张量中的值提取为Python标量，以便进行打印

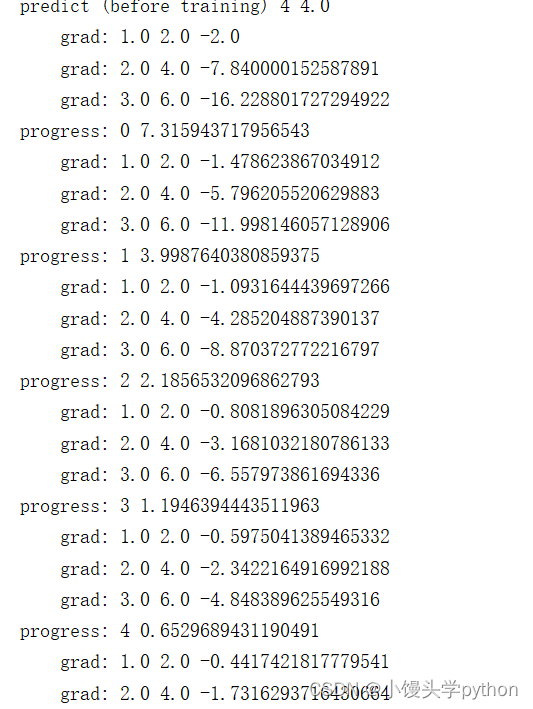
在这里插入图片描述
运行结果如下

🥦反向传播在深度学习中的应用

反向传播算法在深度学习中具有广泛的应用，它使神经网络能够学习复杂的特征和模式，从而在图像分类、自然语言处理、语音识别等各种任务中取得了显著的成就。

以下是反向传播在深度学习中的一些应用：

图像分类：卷积神经网络（CNNs）使用反向传播来学习图像特征，用于图像分类任务。
自然语言处理：循环神经网络（RNNs）和变换器（Transformers）等模型使用反向传播来学习文本数据的语义表示，用于机器翻译、情感分析等任务。
强化学习：在强化学习中，反向传播可以用于训练智能体，使其学会在不同环境中做出合适的决策。
生成对抗网络：生成对抗网络（GANs）使用反向传播来训练生成器和判别器，从而生成逼真的图像、音频或文本。

🥦链式求导法则

在神经网络中，链式求导法则是一个关键的概念，用于计算神经网络中的权重参数的梯度，从而进行反向传播（backpropagation）算法，这是训练神经网络的核心。下面以一个简单的神经网络为例，说明链式求导法则在神经网络中的应用：

假设我们有一个简单的神经网络，包含一个输入层、一个隐藏层和一个输出层。网络的输出可以表示为：

y = f(g(h(x)))

其中：

x 是输入数据。
h(x) 是隐藏层的激活函数。
g(h(x)) 是输出层的激活函数。
f(g(h(x))) 是网络的最终输出。

我们想要计算损失函数关于网络输出 y 的梯度，以便更新网络的权重参数以最小化损失。使用链式求导法则，我们可以将这个问题分解成多个步骤：

首先，计算损失函数关于网络输出 y 的梯度 ∂L/∂y，其中 L 是损失函数。
接下来，计算输出层的激活函数关于其输入的梯度 ∂g(h(x))/∂h(x)。
然后，计算隐藏层的激活函数关于其输入的梯度 ∂h(x)/∂x。
最后，将这些梯度相乘，得到损失函数关于输入数据 x 的梯度 ∂L/∂x，并用它来更新网络的权重参数。

链式求导法则允许我们将整个过程分解为这些步骤，并在每个步骤中计算局部梯度。这是神经网络中反向传播算法的关键，它允许我们有效地更新网络的参数，以便网络能够学习从输入到输出的复杂映射关系。

🥦总结

反向传播是深度学习中的核心算法之一，它使神经网络能够自动学习复杂的特征和模式，从而在各种任务中取得了巨大的成功。理解反向传播的原理和实现对于深度学习从业者非常重要，它是构建和训练神经网络的基础。希望本文对您有所帮助，深入了解反向传播将有助于更好地理解深度学习的工作原理和应用。

本文根据b站刘二大人《PyTorch深度学习实践》完结合集学习后加以整理，文中图文均不属于个人。

请添加图片描述

挑战与创造都是很痛苦的，但是很充实。