一 色块提取方法：

①首先是色彩模型的转换 由RGB颜色空间转到HSV颜色空间
原因：RGB颜色空间适合显示系统，但是各分量间相关性很强，比如当图像亮度发生变化时，RGB三个分量都会发生相应改变 但是HSV颜色空间更能感知颜色的变化，比如说 H=60时 就是黄色 S和V只是决定了黄色的饱和度和明度 所以更适合进行图像分割
另一方面 我处理的多源拼接图像 可能存在的问题 可能是亮度也可能是色彩的不同 所以用HSV分量更适合

 我们观察到多源拼接影像 色块间亮度或者颜色差异很大 但是可能说不知道哪个分量更适合进行图像分割等操作 也许人眼可以看出来比如亮度差异过大的时候 我们采用V分量 色彩差异可以用H或者S 但是为了省掉这个人为选择分量的麻烦 也是为了实现自动化 我们对这三个分量都做处理 然后自动判断哪个结果最好 对HSV三个分量进行下面步骤
②大津法分割图像
我们的目的是获得上下分布的色块 并且是上面全是前景区域 下面全是背景区域
所以用大津法做了一个初步的图像分割

 ③小连通区去除
大津法分割图像以后 上边前景区域还包括很多 背景区域（同样下边背景区域也包括部分前景区域） 所以进行图像闭运算（先膨胀后腐蚀 膨胀的目的是去除上面前景区域的小背景区域 然后再进行相同尺寸的腐蚀让他回到原来的形状 ）
但是 边界周围有很多小的连通区，膨胀以后会破坏边界线信息 影响后续的轮廓拟合 比如b里面分界线周围有小连通区 先膨胀在腐蚀以后边界线会发生变化 所以要在闭运算之前进行小连通区去除
④ 图像闭运算 + 轮廓拟合
小连通区干掉以后，可以进行图像闭运算了 但是这个尺寸如何确定： 我们收集的数据集大多数在500X500左右 闭运算适合的尺寸在30左右 但是为了尽可能适合大多数图像
我们还是设置了一个闭运算的范围 尺寸从10-100 ，然后自动判断出 哪个尺寸的闭运算得到的结果最为符合色块分布
所以这里就要有一个判断标准 判断哪个闭运算尺寸得到的结果最好（最符合色块分布）
什么时候最符合色块分布嘞 我选择的是 均值差 上下色块在某个分量的均值差
比如 b是 H分量 它的上下色块 像素值之间差异是很明显的 上下色块的均值差是最大的
这个最大 是跟 （10-100共10个尺寸）所有闭运算尺寸处理的所有分量 计算出的均值差结果比的
有点抽象（或者我语言表达的不到家） 我们计算了 十个尺寸三个分量 也就是三十个均值差数据
看下面的图 对H分量 尺寸是40和20的结果 计算红黄两个区域的均值差 40的肯定大于20的
这个结论一方面是观察的 另一方面做了几十组实验得到的

 

 闭运算 + 轮廓拟合（用的多边形拟合 因为色块分界线也可能是折线）以后 就得到第一次提取结果了 但是！ 色块也可能有多个！ 所以还要判断色块数目 比如这个 还得继续分割

 

 

二 色块数目判断

色块数目判断目的在于判断提取结果是否是单个色块 不是判断有几个色块
下面的过程也很麻烦。。。 我导非要实现自动化 啥都自动 当初我觉的这是天方夜谭
但是我导说 没有解决不了的问题 （后来跟我师弟也这样说。。）
这一部分的目的就是 尽可能把色块分布表现出来 一步一步简化地物 把真实的色彩分布展示出来

 

 ① 均值分布图
我们研究的区域只针对 前景区域(非黑色区域)
同样 把这两个图像转为HSV 提取HSV三分量 对每个分量
（1）首先 分成50x50 的块 不足50的就忽略不计
（将背景区域先设置为255 这个255是为了让结果看的更明显
从左到右分块 就是右边最后一个不足50就不管他 直接设置为255
从上到下分块 最下面不足50就不管他 设为255）
（2）计算每个块的均值 并用均值代替块内的每个像素
这时候我们已经获得HSV 三个分量 的均值分布图了 但是用哪个分量更能看出有几个色块呢
我把每个分量里面的均值数据分别记成一个集合 如果说是某个分量里面色块差异很明显 那么这个分量的均值数据集合里面的数值一定是变化最剧烈的 我们选择计算标准差来表示各分量中图像块均值数据的离散程度 找到HSV三个分量计算出的对应三个标准差 最大的就是想要找到的那个分量
下面是结果 可以在图一看出一点差别 但差别不是很明显 所以继续

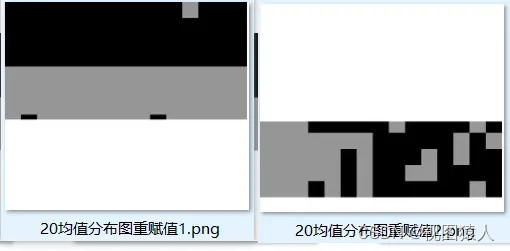
 ②重赋值均值分布图
我们把大津法应用到均值数据集合里面 找到均值数据的阈值 大于阈值的就设为150（纯粹是方便观察） 小于阈值的就设为0 下图就看出来比较明显了

 ③均值分布纠正图
我们继续
我们已经把这个能大致反映色块分布的图稿出来了 根据提取色块时候说的色块间的均值差
单色块间的均值差 会小于 多色块均值差 中间会有一个阈值 以上图为例
图一里面计算 灰色区域和黑色区域这两个区域对于均值数据 的均值差d1
图二里面计算 灰色区域和黑色区域这两个区域对于均值数据 的均值差d2
d1>d2 但是架不住会有些特殊情况 为了更好地判断 我们做了两个预处理
第一个： 比如图2 单色块里面会有一些特殊区域 比如高亮水域建筑物等 会使均值差变大 所以我们把高亮建筑物这些 归类到黑色区域（也就是填充均值数据很大的连通区）
因此当重赋值均值分布图中前景区域存在面积较小的值为150的连通区时，需要将这些连通区填充为背景区域。

 

 

第二个：
在计算差值之前 我们可以通过判断色块形状来剔除掉一部分容易判断的
影像中各个色块一般是由直线或者斜线构成的规则多边形，如果填充后的连通区依然是不规则区域，就说明该连通区不是一个完整的色块，而是在单个色块中的其他类型地物。我们选择根据其面积最大的连通区的边数作进一步判断， （连通区有斜边的时候 会有很多小锯齿 我们先做一个多边形拟合 然后找到面积最大轮廓 然后统计轮廓的边数即可）
据实验得 边数阈值设为25 大于25的就是单色块 小于25的需要继续进行判断

进行上述两个预处理后 我们要开始计算均值差 来判断色块了
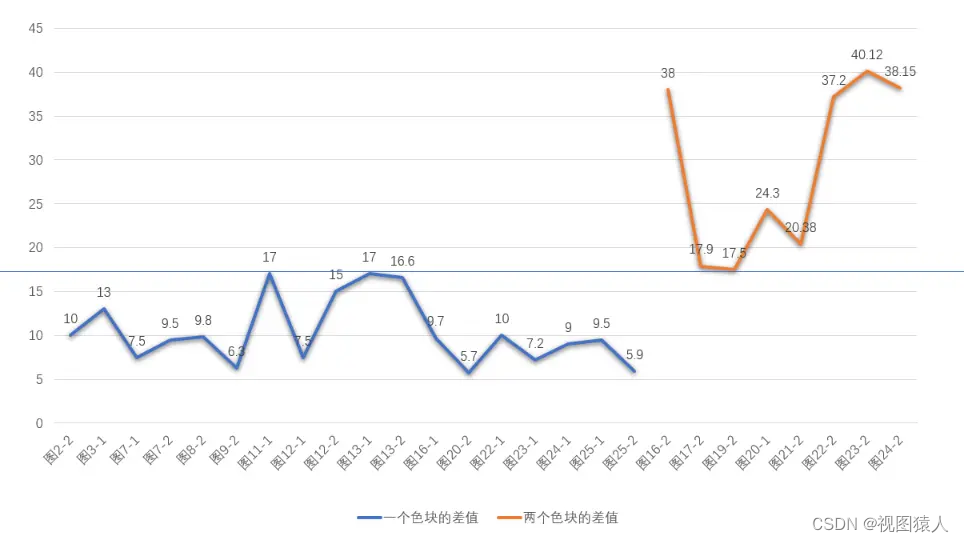
我们根据数据集 里面的数据计算的均值差
做了个折线图 存在阈值17.4