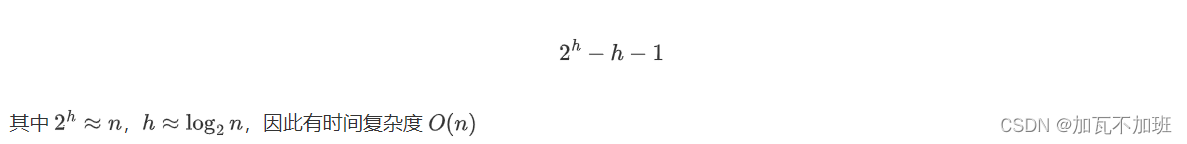文章目录
- 6.1 数组与矩阵
- 6.1.1 数组
- 6.1.2 稀疏矩阵
- 6.2 线性表
- 6.2.1 数据结构的定义
- 6.2.2 顺序表与链表
- 6.2.2.1 定义
- 6.2.2.2 链表的操作
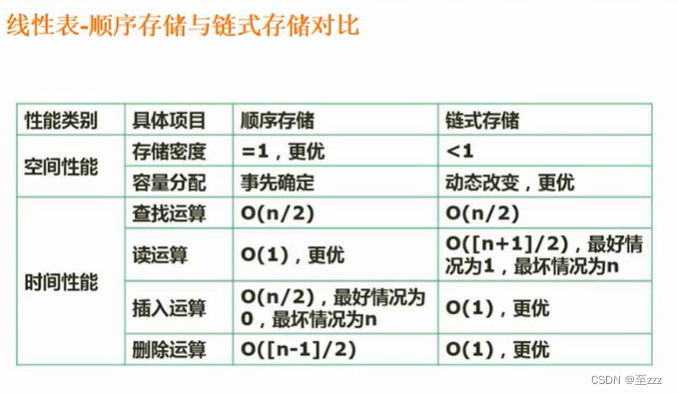
- 6.2.3 顺序存储和链式存储的对比
- 6.2.4 队列、循环队列、栈
- 6.2.4.2 循环队列队空与队满条件
- 6.2.4.3 出入后不可能出现的序列练习
- 6.2.5 串
- 6.3 广义表
- 6.4 树与二叉树
- 6.4.1 基本概念
- 6.4.2 满二叉树与完全二叉树
- 6.4.3 二叉树的重要性质
- 6.4.4 二叉树的遍历
- 6.4.5 方向构造二叉树
- 6.4.6 树转二叉树
- 6.4.7 查找二叉树(排序二叉树)
- 6.4.8 最优二叉树(哈夫曼树)
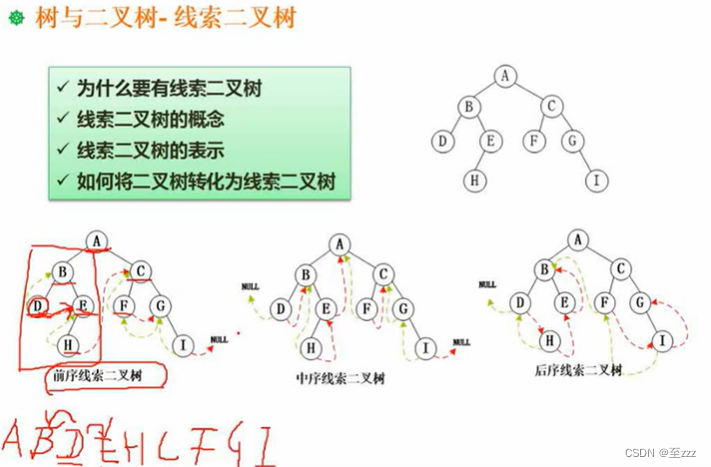
- 6.4.9 线索二叉树
- 6.5 图
- 6.6 排序与查找
- 6.7 算法基础及常见的算法
6.1 数组与矩阵
6.1.1 数组
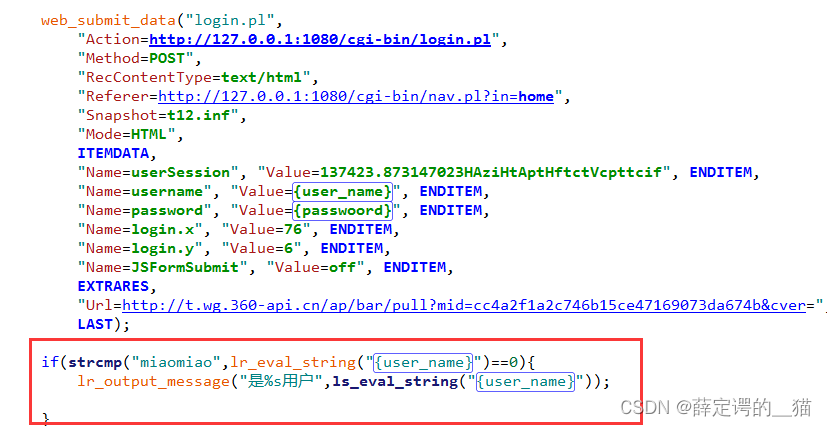
求存储地址
- 一维数组直接算
- 二维数组看清是按行还是按列存储
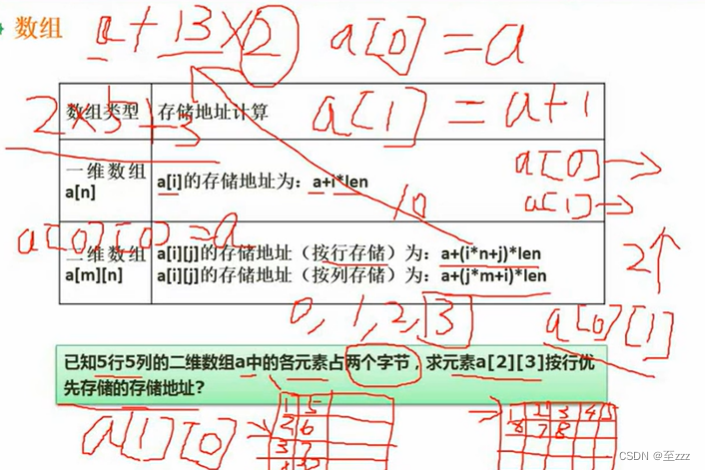
6.1.2 稀疏矩阵
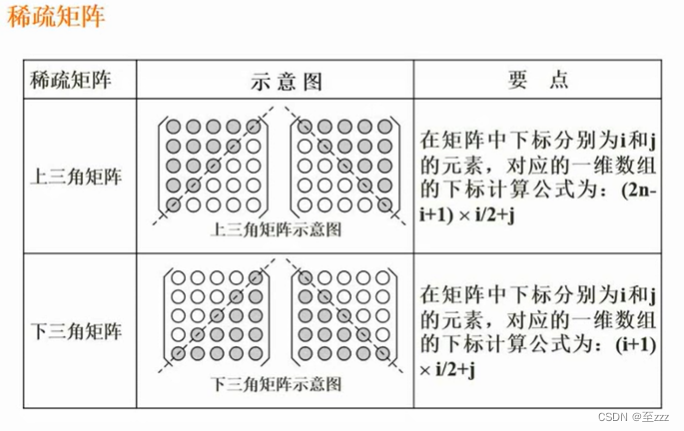
求对应一维数组下标公式,可以直接代两个元素进行验算

6.2 线性表
6.2.1 数据结构的定义
线性结构
- 线性表
非线性结构
- 树
- 图(可能存在环路)

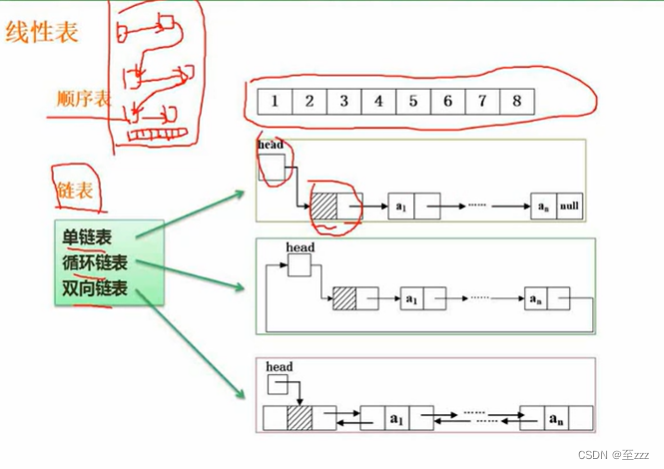
6.2.2 顺序表与链表
6.2.2.1 定义
顺序表:采用一维数组的方式来存信息
链表:每个存储单元包含数据和指针
- 单链表:只有一套指针,头结点指向第一个元素,并依次指下去。
- 循环链表:与单链表的区别就是尾部有个指针直接指向头部。
- 双向链表:可以双向移动,一套指针从头指到尾部,一套由尾指到头部。
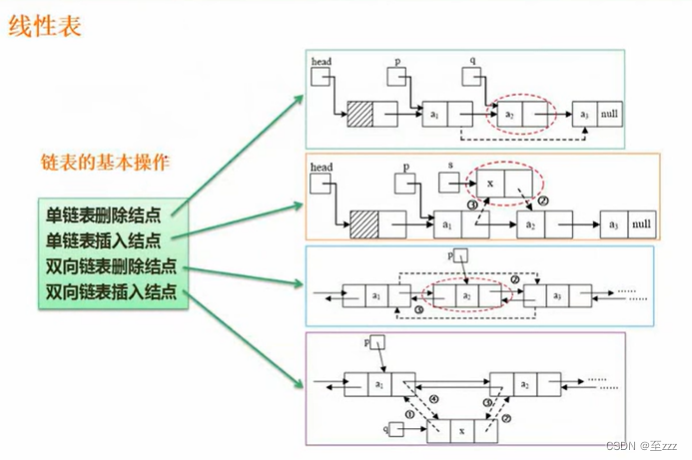
6.2.2.2 链表的操作
- 单链表删除结点:
p->next = q->next- 单链表插入结点:
s->next = p->next;p->next = s->next
引入头结点的好处可以让所有的结点操作方式一致
6.2.3 顺序存储和链式存储的对比
6.2.4 队列、循环队列、栈
队列:先进先出(又称先进先出表)
栈:先进后出
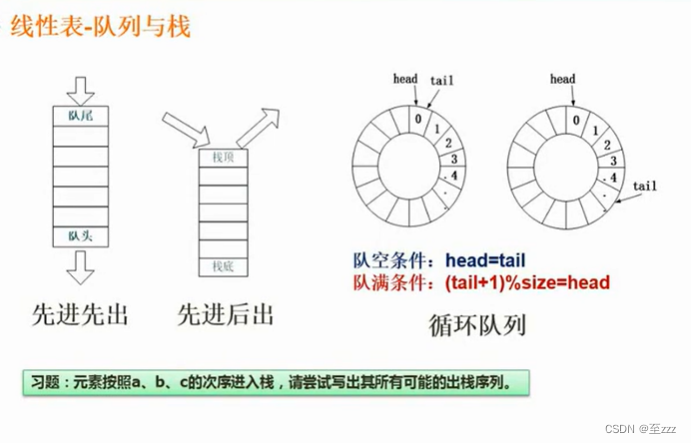
6.2.4.2 循环队列队空与队满条件

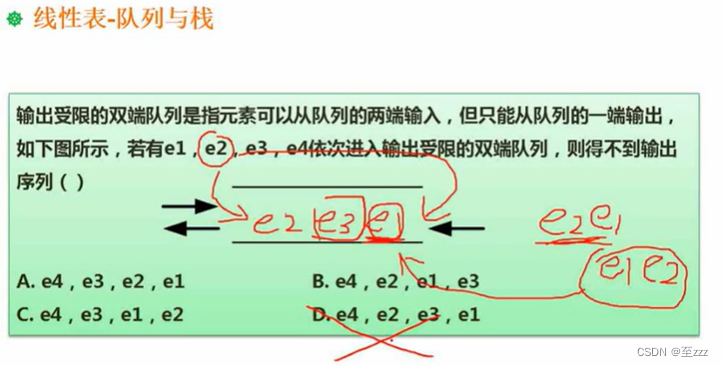
6.2.4.3 出入后不可能出现的序列练习
6.2.5 串
串是仅由字符构成的有限序列,是线性表的一种。
6.3 广义表
- 广义表是线性表的推广
- 广义表的元素即可以是单个元素(原子),也可以是广义表(子表)
- 操作:
*取表头head(LS)
*取表尾tail(LS)

6.4 树与二叉树
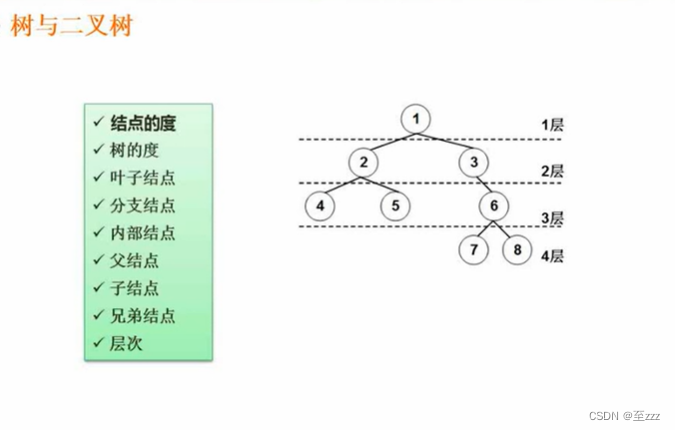
6.4.1 基本概念
- 根:树最顶层的结点。即下图的结点1。
- 父结点(双亲结点):元素的上一层。下图中结点1为结点2、3的父结点。
- 子结点:与父结点相反。
- 兄弟结点:与该结点同层。下图结点4是结点5的兄弟结点。6为堂兄弟结点。
- 结点的度:一个结点的子树的个数。下图结点2的度为2,结点7的度为0。
- 树的度:该树中结点的度最高的结点的度的个数。MAX。下图树的度为2。
- 叶子结点(终端结点):度为0的结点。下图结点4、5、7、8。
- 内部结点(分支结点或非终端结点):除根结点和叶子结点外。下图结点2、3、6。
- 结点的层次:根结点为第一层,依次往下。
- 树的高度(深度):一棵树最大的层数。下图树的高度为4。
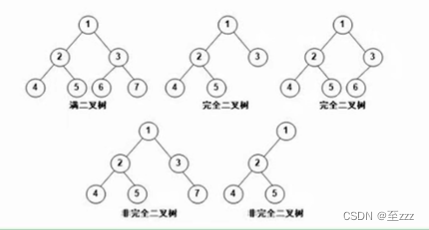
6.4.2 满二叉树与完全二叉树
- 满二叉树:深度为k的二叉树节点个数为2k -1,即所有的结点都是满的。
可以对满二叉树进行连续编号,约定编号从根结点自上而下,自左至右依次进行。
- 完全二叉树:除最底层外其余为满二叉树,最底层从左至右依次排列。
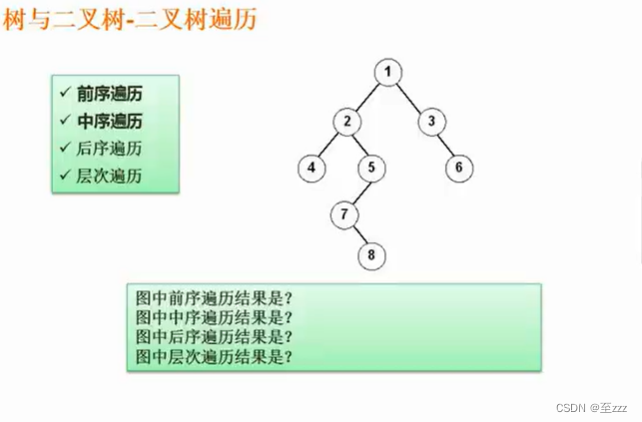
6.4.3 二叉树的重要性质

6.4.4 二叉树的遍历
三种遍历方式的区别就是根遍历的先后问题。
- 先序遍历:根左右
- 中序遍历:左根右
- 后序遍历:左右根
- 层次遍历:按顺序遍历
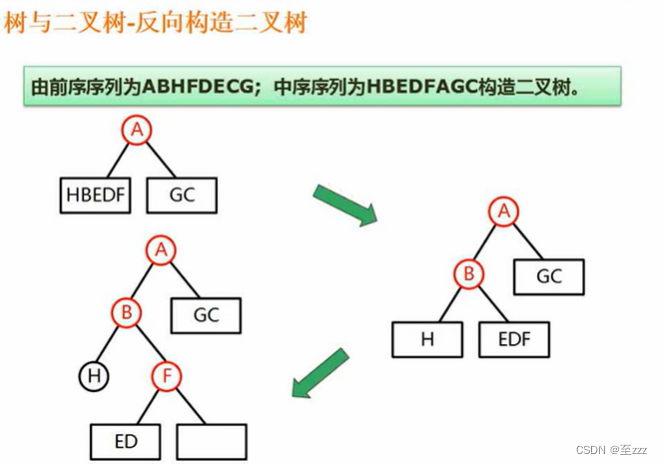
6.4.5 方向构造二叉树
给出二叉树的遍历序列,反向推出二叉树的结构
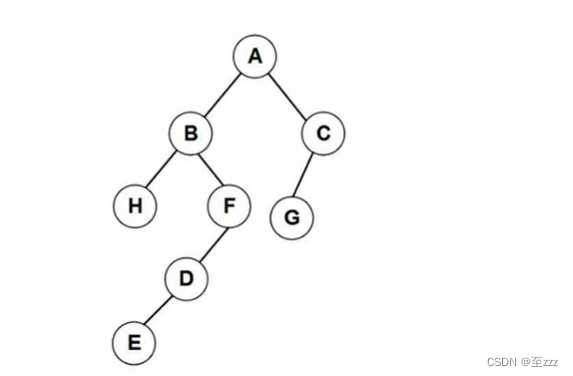
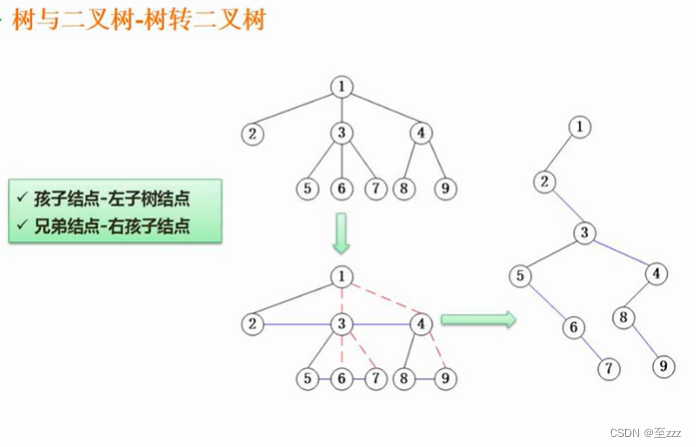
6.4.6 树转二叉树
- 将兄弟结点相连。
- 只保留第一个孩子结点与父结点的连线,其余全部断开,在旋转图可得
6.4.7 查找二叉树(排序二叉树)
对于每个结点,其左孩子结点小于根,右孩子结点大于根,称为查找二叉树。

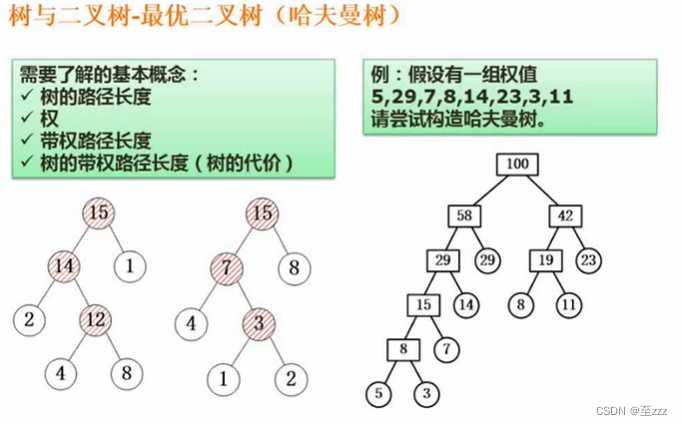
6.4.8 最优二叉树(哈夫曼树)
哈夫曼树是其叶子结点带权路径长度最短的二叉树。
- 带权路径长度:即路径长度乘权值,下图第一个二叉树的结点8的带权路径长度为8*3=24。
- 树的带权路径长度为其总和。
6.4.9 线索二叉树