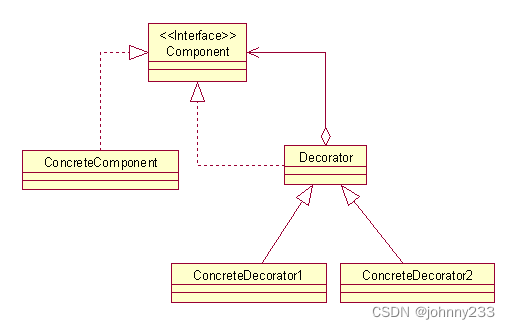
字典树的定义
字典树是一个用来快速查找和存储字符串集合的数据结构。
字典树的形状
假设我们字典树里有以下5个单词：
akio，akno，cspj，csps，trie
那么字典树长这样：
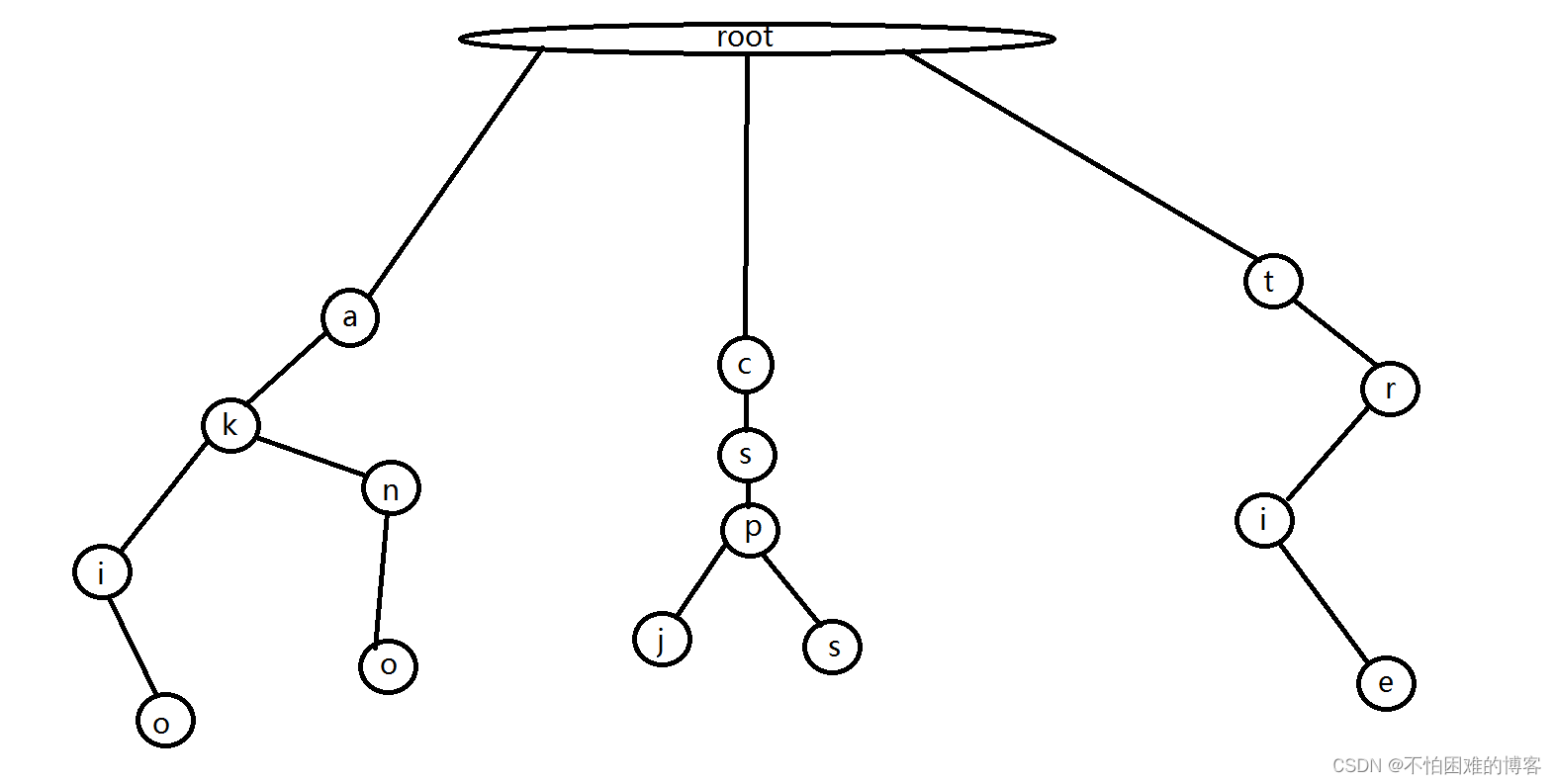trie 的结构非常好懂，我们用(u,c) 表示结点 u 的 c 字符指向的下一个结点，或着说是结点 u 代表的字符串后面添加一个字符 c 形成的字符串的结点。（c 的取值范围和字符集大小有关，不一定是 26。）
既然字典树支持高效查找和存储，让我们看看怎么查找和存储。
查找操作
我们把每一个单词最后结尾的字符记录一下（用cnt数组）。
比如说我们查找一个字符串apio。
我们首先沿着a边发现a在字典树里，但是b不在字典树里，所以字符串apio不在字典树里。
再比如我们查找一个字符串akioi。
我们沿着akio的路径发现akio都在字典树里，但是结尾是o而非i，所以字符串akioi不在字典树里。
具体操作
依次遍历字符串str的所有字符，如果父节点的所有子节点里没有字符str[i],证明str不在字典树里，如果在返回true，否则返回false。
模板代码
int son[N][26];//存储trie树里面每个节点的所有儿子
int cnt[N];//以当前节点为子节点的单词个数。
int idx;//当前用的哪一下标。
//下标是0的点，既是根节点，又是空节点。
int query(char str[]) {
int p = 0;
for(int i = 0; str[i]; i++) {
int u = str[i] - 'a';
if(!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
存储操作
我们先查找当前str是否在字典树里，如果是，计数++，如果不是，创建一条新路径以存储str。
这个模板代码和查询非常像。
模板代码
int son[N][26];//存储trie树里面每个节点的所有儿子
int cnt[N];//以当前节点为子节点的单词个数。
int idx;//当前用的哪一下标。
//下标是0的点，既是根节点，又是空节点
int query(char str[]) {
int p = 0;
for(int i = 0; str[i]; i++) {
int u = str[i] - 'a';
if(!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
例题A
835. Trie字符串统计
维护一个字符串集合，支持两种操作：
I x 向集合中插入一个字符串 x；
Q x 询问一个字符串在集合中出现了多少次。
共有 N个操作，所有输入的字符串总长度不超过 105，字符串仅包含小写英文字母。
输入格式
第一行包含整数 N，表示操作数。接下来 N行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。
输出格式
对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x
在集合中出现的次数。
每个结果占一行。
数据范围
1
≤
N
≤
2
∗
1
0
4
1≤N≤2∗10^4
1≤N≤2∗104
输入样例：
5
I abc
Q abc
Q ab
I ab
Q ab
输出样例：
1
0
1
利用上面的模板，秒了这题
AC代码：
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int son[N][26];//存储trie树里面每个节点的所有儿子
int cnt[N];//以当前节点为子节点的单词个数。
int idx;//当前用的哪一下标。
//下标是0的点，既是根节点，又是空节点。
char str[N];
void insert(char str[]) {
int p = 0;
int len = strlen(str);
for(int i = 0; i < len; i++) {
int u = str[i] - 'a';
if(!son[p][u]) son[p][u] = ++idx;
p = son[p][u];
}
cnt[p]++;
}
int query(char str[]) {
int p = 0;
int len = strlen(str);
for(int i = 0; i < len; i++) {
int u = str[i] - 'a';
if(!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
int main() {
int n;
scanf("%d", &n);
while(n--) {
char op[2];
scanf("%s%s", op, str);
if(op[0] == 'I') insert(str);
else printf("%d\n", query(str));
}
}
例题B:
143. 最大异或对
在给定的 N个整数 A1，A2……AN中选出两个进行 xor（异或）运算，得到的结果最大是多少？
输入格式
第一行输入一个整数 N。
第二行输入 N 个整数 A1～AN。
输出格式
输出一个整数表示答案。
数据范围
1
≤
N
≤
1
0
5
1≤N≤10^5
1≤N≤105,
0
≤
A
i
<
2
31
0≤Ai<2^{31}
0≤Ai<231
输入样例：
3
1 2 3
输出样例：
3
将a[i]变成01序列（2进制），正常建树。
AC代码如下：
#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 3100010;
int n;
int a[N], son[M][2], idx;
void insert(int x) {
int p = 0;
for (int i = 30; i >= 0; i--) {
int &s = son[p][x >> i & 1];
if (!s) s = ++idx;
p = s;
}
}
int search(int x) {
int p = 0, res = 0;
for (int i = 30; i >= 0; i--) {
int s = x >> i & 1;
if (son[p][!s]) {
res += 1 << i;
p = son[p][!s];
} else p = son[p][s];
}
return res;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &a[i]);
insert(a[i]);
}
int res = 0;
for (int i = 0; i < n; i++) res = max(res, search(a[i]));
printf("%d\n", res);
return 0;
}
总结
trie树是一种字符串类的数据结构，一般字符串在题目中都限制严格（字母，01序列等）。时间复杂度 O ( ∣ S ∣ ) O(|S|) O(∣S∣).
