文章目录
- 0 前言
- 1 项目背景
- 2 算法架构
- 3 FP-Growth算法原理
- 3.1 FP树
- 3.2 算法过程
- 3.3 算法实现
- 3.3.1 构建FP树
- 3.4 从FP树中挖掘频繁项集
- 4 系统设计展示
- 5 最后
0 前言
🔥 优质竞赛项目系列,今天要分享的是
基于FP-Growth的新闻挖掘算法系统的设计与实现
该项目较为新颖,适合作为竞赛课题方向,学长非常推荐!
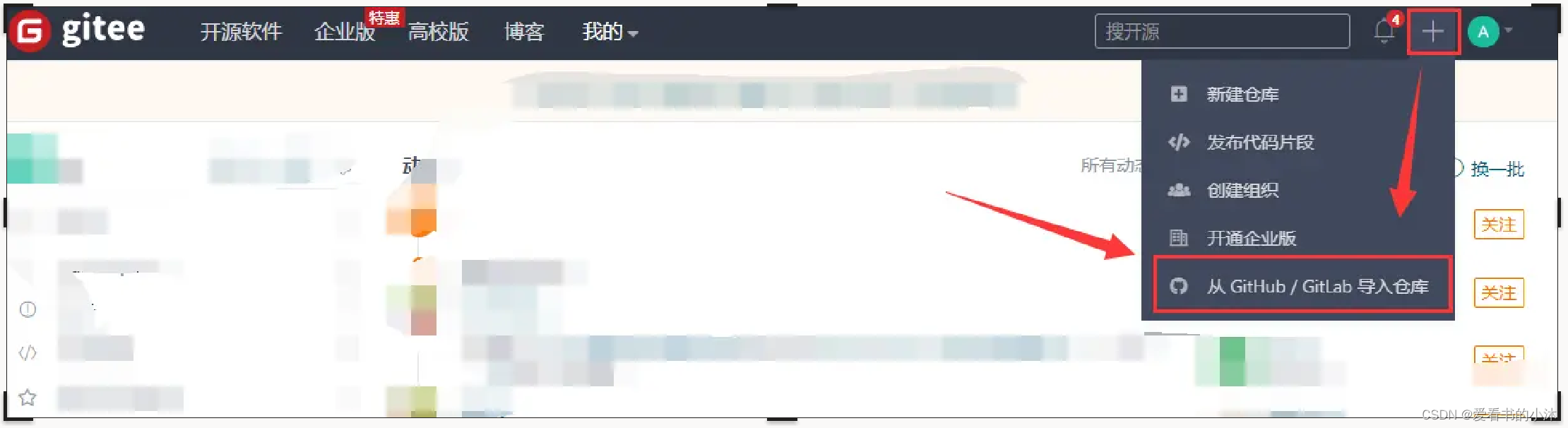
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
1 项目背景
如今新闻泛滥,令人眼花缭乱,即使同一话题下的新闻也多得数不胜数。人们可以根据自己的职业和爱好关注专业新闻网站的不同热点要闻。因此,通过对人们关注新闻的热点问题进行分析,可以得出民众对某个领域的关切程度和社会需要解决的问题,也有利于了解当前的舆论焦点,有助于政府了解民意,便于国家对舆论进行正确引导,使我们的社会更加安定和谐。本文以财经领域为例,通过爬虫技术抓取网络上的大量财经新闻,通过对新闻内容文本进行预处理及密度聚类分析来发现热点;从发现的热点中,再进行词汇聚类分析,得出热点所涉及的人或事物,以此分析出社会对经济领域关注的问题和需要解决的问题。

2 算法架构
该项目学长要通过文本挖掘技术进行新闻热点问题分析,把从网上抓取到的财经新闻,通过对新闻内容的聚类,得到新闻热点;再对热点进行分析,通过对某一热点相关词汇的聚类,得到热点问题所涉及的人物、行业或组织等。

1、利用新闻 API、爬虫算法、多线程并行技术,抓取三大专业财经新闻网站(新浪财经、搜狐财经、新华网财经)的大量财经新闻报道;
2、对新闻进行去重、时间段过滤,然后对新闻内容文本进行 jieba
分词并词性标注,过滤出名词、动词、简称等词性,分词前使用自定义的用户词词典增加分词的准确性,分词后使用停用词词典、消歧词典、保留单字词典过滤掉对话题无关并且影响聚类准确性的词,建立每篇新闻的词库,利用
TF-IDF 特征提取之后对新闻进行 DBSCAN 聚类,并对每个类的大小进行排序;
3、针对聚类后的每一类新闻,为了得到该处热点的话题信息,还需要提取它们的标题,利用 TextRank
算法,对标题的重要程度进行排序,用重要性最高的标题来描述该处热点的话题
4、对所有的新闻内容进行 jieba 分词,并训练出 word2vec 词嵌入模型,然后对聚类后的每一类新闻,提取它们的内容分词后的结果,运用
word2vec 模型得到每个词的词向量,再利用 FP-Growth类算法进行相关新闻挖掘。
3 FP-Growth算法原理
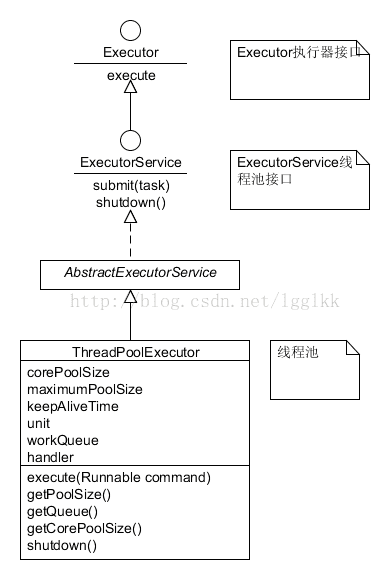
3.1 FP树
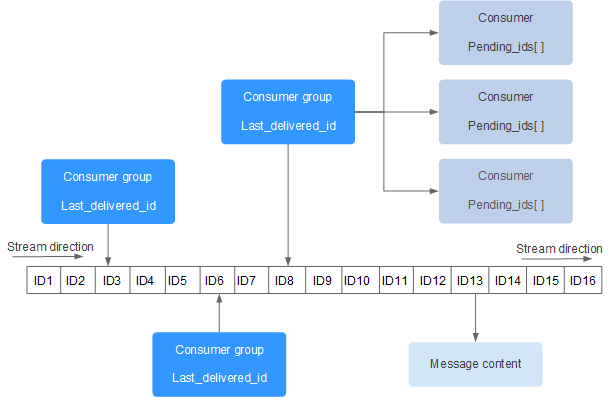
FP树是一种存储数据的树结构,如下图所示,每一路分支表示数据集的一个项集,数字表示该元素在某分支中出现的次数

3.2 算法过程
1 构建FP树
- 遍历数据集获得每个元素项的出现次数,去掉不满足最小支持度的元素项
- 构建FP树:读入每个项集并将其添加到一条已存在的路径中,若该路径不存在,则创建一条新路径(每条路径是一个无序集合)
2 从FP树中挖掘频繁项集
- 从FP树中获得条件模式基
- 利用条件模式基构建相应元素的条件FP树,迭代直到树包含一个元素项为止
算法过程写得比较简略,具体过程我们在下节的实操中进一步理解。
3.3 算法实现
3.3.1 构建FP树
class treeNode:
def __init__(self,nameValue,numOccur,parentNode):
self.name=nameValue #节点名
self.count=numOccur #节点元素出现次数
self.nodeLink=None #存放节点链表中,与该节点相连的下一个元素
self.parent=parentNode
self.children={} #用于存放节点的子节点,value为子节点名
def inc(self,numOccur):
self.count+=numOccur
def disp(self,ind=1):
print(" "*ind,self.name,self.count) #输出一行节点名和节点元素数,缩进表示该行节点所处树的深度
for child in self.children.values():
child.disp(ind+1) #对于子节点,深度+1
# 构造FP树
# dataSet为字典类型,表示探索频繁项集的数据集,keys为各项集,values为各项集在数据集中出现的次数
# minSup为最小支持度,构造FP树的第一步是计算数据集各元素的支持度,选择满足最小支持度的元素进入下一步
def createTree(dataSet,minSup=1):
headerTable={}
#遍历各项集,统计数据集中各元素的出现次数
for key in dataSet.keys():
for item in key:
headerTable[item]=headerTable.get(item,0)+dataSet[key]
#遍历各元素,删除不满足最小支持度的元素
for key in list(headerTable.keys()):
if headerTable[key]<minSup:
del headerTable[key]
freqItemSet=set(headerTable.keys())
#若没有元素满足最小支持度要求,返回None,结束函数
if len(freqItemSet)==0:
return None,None
for key in headerTable.keys():
headerTable[key]=[headerTable[key],None] #[元素出现次数,**指向每种项集第一个元素项的指针**]
retTree=treeNode("Null Set",1,None) #初始化FP树的顶端节点
for tranSet,count in dataSet.items():
localD={} #存放每次循环中的频繁元素及其出现次数,便于利用全局出现次数对各项集元素进行项集内排序
for item in tranSet:
if item in freqItemSet:
localD[item]=headerTable[item][0]
if len(localD)>0:
orderedItems=[v[0] for v in sorted(localD.items(),key=operator.itemgetter(1),reverse=True)] #根据元素全局出现次数对每个项集(tranSet)中的元素进行排序
updateTree(orderedItems,retTree,headerTable,count) #使用排序后的项集对树进行填充
return retTree,headerTable
#树的更新函数
#items为按出现次数排序后的项集,是待更新到树中的项集;count为items项集在数据集中的出现次数
#inTree为待被更新的树;headTable为头指针表,存放满足最小支持度要求的所有元素
def updateTree(items,inTree,headerTable,count):
#若项集items当前最频繁的元素在已有树的子节点中,则直接增加树子节点的计数值,增加值为items[0]的出现次数
if items[0] in inTree.children:
inTree.children[items[0]].inc(count)
else:#若项集items当前最频繁的元素不在已有树的子节点中(即,树分支不存在),则通过treeNode类新增一个子节点
inTree.children[items[0]]=treeNode(items[0],count,inTree)
#若新增节点后表头表中没有此元素,则将该新增节点作为表头元素加入表头表
if headerTable[items[0]][1]==None:
headerTable[items[0]][1]=inTree.children[items[0]]
else:#若新增节点后表头表中有此元素,则更新该元素的链表,即,在该元素链表末尾增加该元素
updateHeader(headerTable[items[0]][1],inTree.children[items[0]])
#对于项集items元素个数多于1的情况,对剩下的元素迭代updateTree
if len(items)>1:
updateTree(items[1::],inTree.children[items[0]],headerTable,count)
#元素链表更新函数
#nodeToTest为待被更新的元素链表的头部
#targetNode为待加入到元素链表的元素节点
def updateHeader(nodeToTest,targetNode):
#若待被更新的元素链表当前元素的下一个元素不为空,则一直迭代寻找该元素链表的末位元素
while nodeToTest.nodeLink!=None:
nodeToTest=nodeToTest.nodeLink #类似撸绳子,从首位一个一个逐渐撸到末位
#找到该元素链表的末尾元素后,在此元素后追加targetNode为该元素链表的新末尾元素
nodeToTest.nodeLink=targetNode
测试
#加载简单数据集
def loadSimpDat():
simpDat = [['r', 'z', 'h', 'j', 'p'],
['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
['z'],
['r', 'x', 'n', 'o', 's'],
['y', 'r', 'x', 'z', 'q', 't', 'p'],
['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
return simpDat
#将列表格式的数据集转化为字典格式
def createInitSet(dataSet):
retDict={}
for trans in dataSet:
retDict[frozenset(trans)]=1
return retDict
simpDat=loadSimpDat()
dataSet=createInitSet(simpDat)
myFPtree1,myHeaderTab1=createTree(dataSet,minSup=3)
myFPtree1.disp(),myHeaderTab1
输入数据:

由此数据集构建的FP树长这样,看看是不是满足上一节介绍的FP树结构

3.4 从FP树中挖掘频繁项集
具体过程如下:
1 从FP树中获得条件模式基
- 条件模式基:以所查找元素项为结尾的路径集合,每条路径都是一条前缀路径,路径集合包括前缀路径和路径计数值。
- 例如,元素"r"的条件模式基为 {x,s}2,{z,x,y}1,{z}1
- 前缀路径:介于所查找元素和树根节点之间的所有内容
- 路径计数值:等于该条前缀路径的起始元素项(即所查找的元素)的计数值
2 利用条件模式基构建相应元素的条件FP树
- 对每个频繁项,都要创建一棵条件FP树。
- 例如对元素t创建条件FP树:使用获得的t元素的条件模式基作为输入,利用构建FP树相同的逻辑构建元素t的条件FP树
3 迭代步骤(1)(2),直到树包含一个元素项为止
-
接下来继续构建{t,x}{t,y}{t,z}对应的条件FP树(tx,ty,tz为t条件FP树的频繁项集),直到条件FP树中没有元素为止
-
至此可以得到与元素t相关的频繁项集,包括2元素项集、3元素项集。。。
#由叶节点回溯该叶节点所在的整条路径 #leafNode为叶节点,treeNode格式;prefixPath为该叶节点的前缀路径集合,列表格式,在调用该函数前注意prefixPath的已有内容 def ascendTree(leafNode,prefixPath): if leafNode.parent!=None: prefixPath.append(leafNode.name) ascendTree(leafNode.parent,prefixPath) #获得指定元素的条件模式基 #basePat为指定元素;treeNode为指定元素链表的第一个元素节点,如指定"r"元素,则treeNode为r元素链表的第一个r节点 def findPrefixPath(basePat,treeNode): condPats={} #存放指定元素的条件模式基 while treeNode!=None: #当元素链表指向的节点不为空时(即,尚未遍历完指定元素的链表时) prefixPath=[] ascendTree(treeNode,prefixPath) #回溯该元素当前节点的前缀路径 if len(prefixPath)>1: condPats[frozenset(prefixPath[1:])]=treeNode.count #构造该元素当前节点的条件模式基 treeNode=treeNode.nodeLink #指向该元素链表的下一个元素 return condPats #有FP树挖掘频繁项集 #inTree: 构建好的整个数据集的FP树 #headerTable: FP树的头指针表 #minSup: 最小支持度,用于构建条件FP树 #preFix: 新增频繁项集的缓存表,set([])格式 #freqItemList: 频繁项集集合,list格式 def mineTree(inTree,headerTable,minSup,preFix,freqItemList): #按头指针表中元素出现次数升序排序,即,从头指针表底端开始寻找频繁项集 bigL=[v[0] for v in sorted(headerTable.items(),key=lambda p:p[1][0])] for basePat in bigL: #将当前深度的频繁项追加到已有频繁项集中,然后将此频繁项集追加到频繁项集列表中 newFreqSet=preFix.copy() newFreqSet.add(basePat) print("freqItemList add newFreqSet",newFreqSet) freqItemList.append(newFreqSet) #获取当前频繁项的条件模式基 condPatBases=findPrefixPath(basePat,headerTable[basePat][1]) #利用当前频繁项的条件模式基构建条件FP树 myCondTree,myHead=createTree(condPatBases,minSup) #迭代,直到当前频繁项的条件FP树为空 if myHead!=None: mineTree(myCondTree,myHead,minSup,newFreqSet,freqItemList)
接着刚才构建的FP树,测试一下,
freqItems=[]
mineTree(myFPtree1,myHeaderTab1,3,set([]),freqItems)
freqItems
我们从FP树中挖掘到的频繁项集如下,这里设置的最小支持度为3:

上图表示数据集中,支持度大于3(出现3次以上)的元素项集,即,频繁项集。
4 系统设计展示
为了方便操作及理解,学长使用 Python 的 tkinter 模块设计了一个系统操作界面

分析可视化




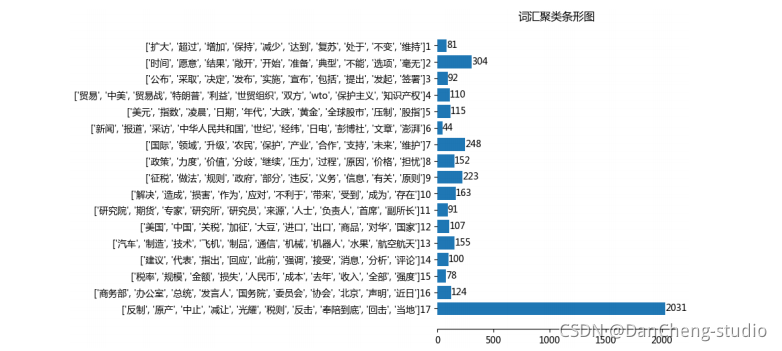
(未完待续。。。。)
5 最后
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate