【LeetCode刷题笔记】二维数组

498.对角线遍历

解题思路：

简化问题，首先考虑按照逐条对角线打印元素，而不考虑翻转的情况。
M 行 N 列的二维矩阵总共有 M + N - 1 条对角线（ 右上 -> 左下 ）
1）如何遍历： 从左往右遍历 对角线的条数，总共遍历 M + N - 1 轮，d：[0， M + N - 1 ） 每一轮中确定当前对角线 d 的右上角的点的坐标 （x, y） ，然后 将这个点作为起始点出发，再起一个 while 循环，按照 x++, y-- 的方式，即 右上 -> 左下的方向，遍历矩阵位于该对角线上的点，并保存到结果数组中 res[i++] = matrix[x][y] ， while 循环的判断条件： x < M && y >= 0 即二者都没有越界就一直循环直到越界为止。
2）如何折线保存： d%2 == 0 时需要 反向保存，因此这时可以搞一个 list ，然后 Collections.reverse(list) 再保存，或者，每次开始内层遍历对角线的 while 循环前记下res数组当前位置作为 start ， while 循环结束时res的 i 下标就是结束位置，反转 res[start...i] 这一段区间即可（这里可以写一个 reverse 数组区间的函数）。
3）如何确定 对角线 d 的右上角的点的坐标： 其实所有对角线右上角的点就是整个矩阵中位于最上边一行和位于最右边一列的那些点，因此当 d < N 时，所求的点的 x 坐标都是 0 ， y 坐标则是 d ，即 [ 0， d] ，而当 d >= N 时，所求的点的 x 坐标是 d - ( N - 1 ) ， y 坐标全都是 N - 1 ，即 [ d - ( N - 1 ) ， N - 1] 。

如下图所示：

这个题最大的难处就是首先要观察出一个二维矩阵的右对角线的条数是 M + N - 1，因为这是我们要遍历的对角线的轮数。其次，我们要确定出每条对角线右上角的坐标（x，y），将它用对角线下标等价计算出来。（为什么呢，因为我们是对对角线进行遍历，此时拿不到每个点的二维坐标，所以需要转换）

为了看的更清楚一些，我们把矩阵中的数字都去掉：

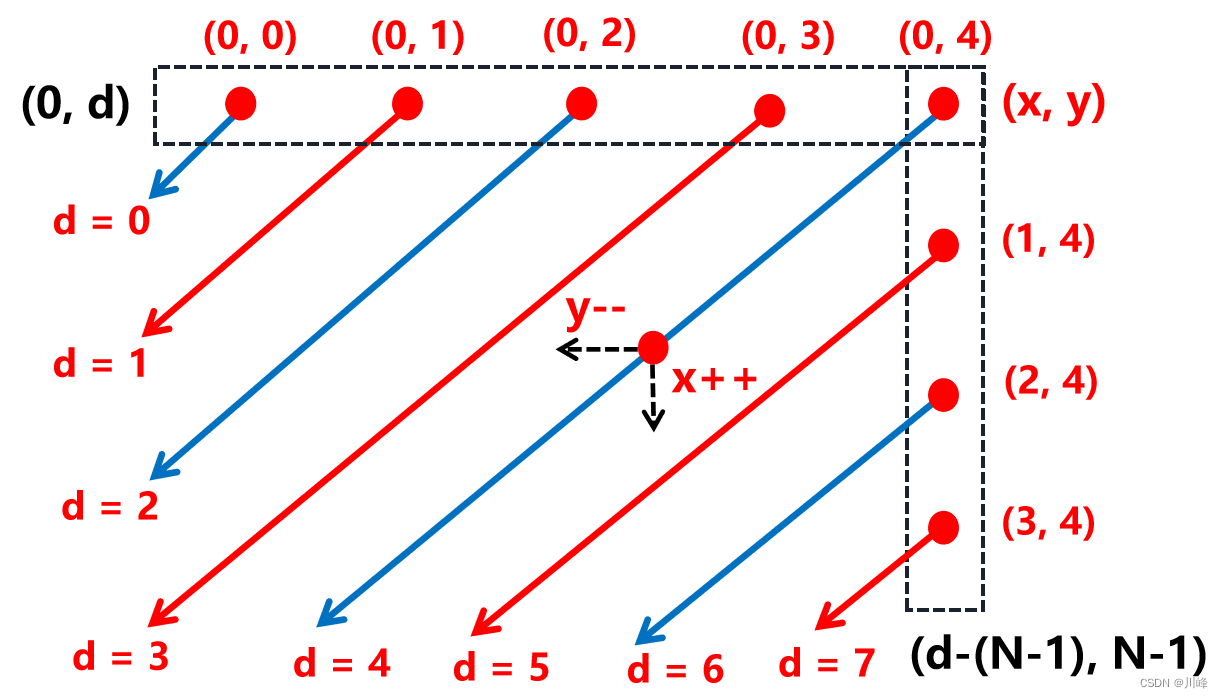
其实最上面一行的对角线起始点坐标就是二维矩阵的第一行的坐标点，它们的横坐标都是 0，而纵坐标就是该点的二维矩阵的列下标，可以认为是（0，j），但是我们在遍历的时候，是遍历的对角线的轮数 [0, M + N - 1]，而非一般的双重for循环那样遍历二维矩阵的形式（如果是那样就能拿到 i 和 j），所以第一行的对角线起始点坐标需要利用对角线的轮数下标来等价计算，它正好是 （0，d）。

同样的，最后一列的对角线起始点其实就是二维矩阵的最后一列的坐标点（i, N - 1），我们也需要用对角线的下标来等价计算出来，它是（d - (N - 1), N - 1）。

最后，在保存答案的时候，需要用到一个小小的伎俩，那就是第奇数条对角线（或者说对角线下标是d=0、2、4...的）上的值，逆序保存就可以了。也就是上面图中蓝色的对角线，应该是下面这样：

54.螺旋矩阵

解题思路：

1）按层/环访问：上右下左四条边循环访问，设4个变量分别表示上下左右边界：T = 0，B = M - 1，L = 0， R = N - 1，
首先在最外层使用一个while循环控制四个方向不越界: T < B && L < R ，
然后在每次循环中，使用4个for循环分别收集上下左右四条边上的值，在收集完后四条边同时向内收缩一圈 T++ B-- L++ R--，
最后跳出while循环时，只会剩下一行 T==B 或者只剩一列 L==R ，将其收集即可。

如下图所示：

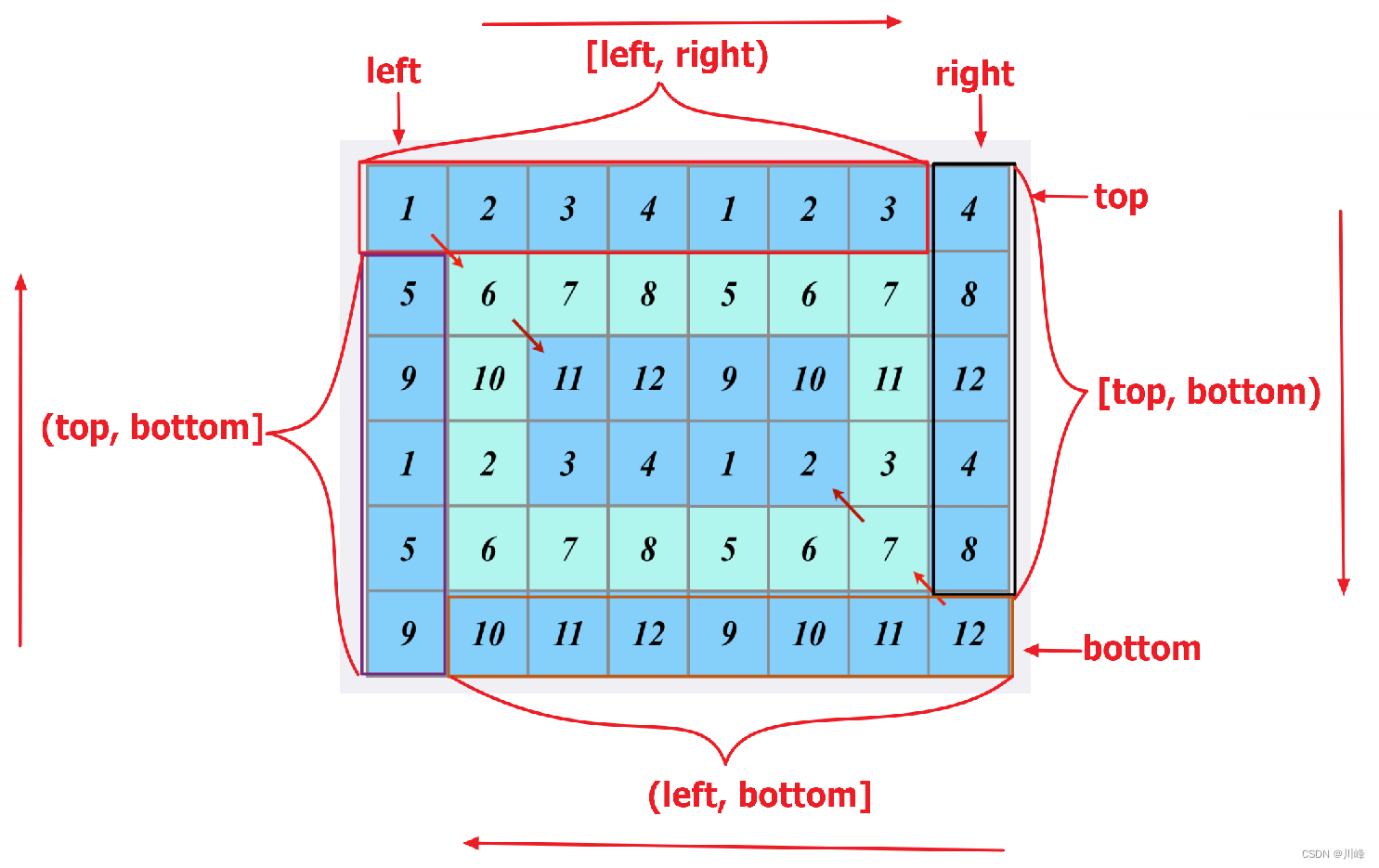
例如在收集上边一行时，使用for循环遍历区间 i: [L, R)，此时的横坐标固定为 T，遍历的下标是列坐标，所以for循环中每个元素的取值为matrix[T][i]。类似的，对于右边的收集 i: [T, B)，元素的取值为matrix[i][R]；对于下边的收集 i: [R, L)，元素的取值为matrix[B][i]；对于左边的收集 i: [B, T) ，元素的取值为matrix[i][L]。

最后收缩到最内层时，只会剩下一行或者只会剩下一列，如下图所示：

上面代码中有一点需要注意，最后只剩一行或只剩一列的情况，只能写成 if...else if... 的形式，不能写成两个 if 并排判断的形式。因为对于题目示例1那样的正方形矩阵，最后只会剩下一个点，此时 T==B 或者 L==R 会同时满足，如果写成两个 if 并排判断的形式，就会多收集一次这个点，导致错误答案。

解题思路：

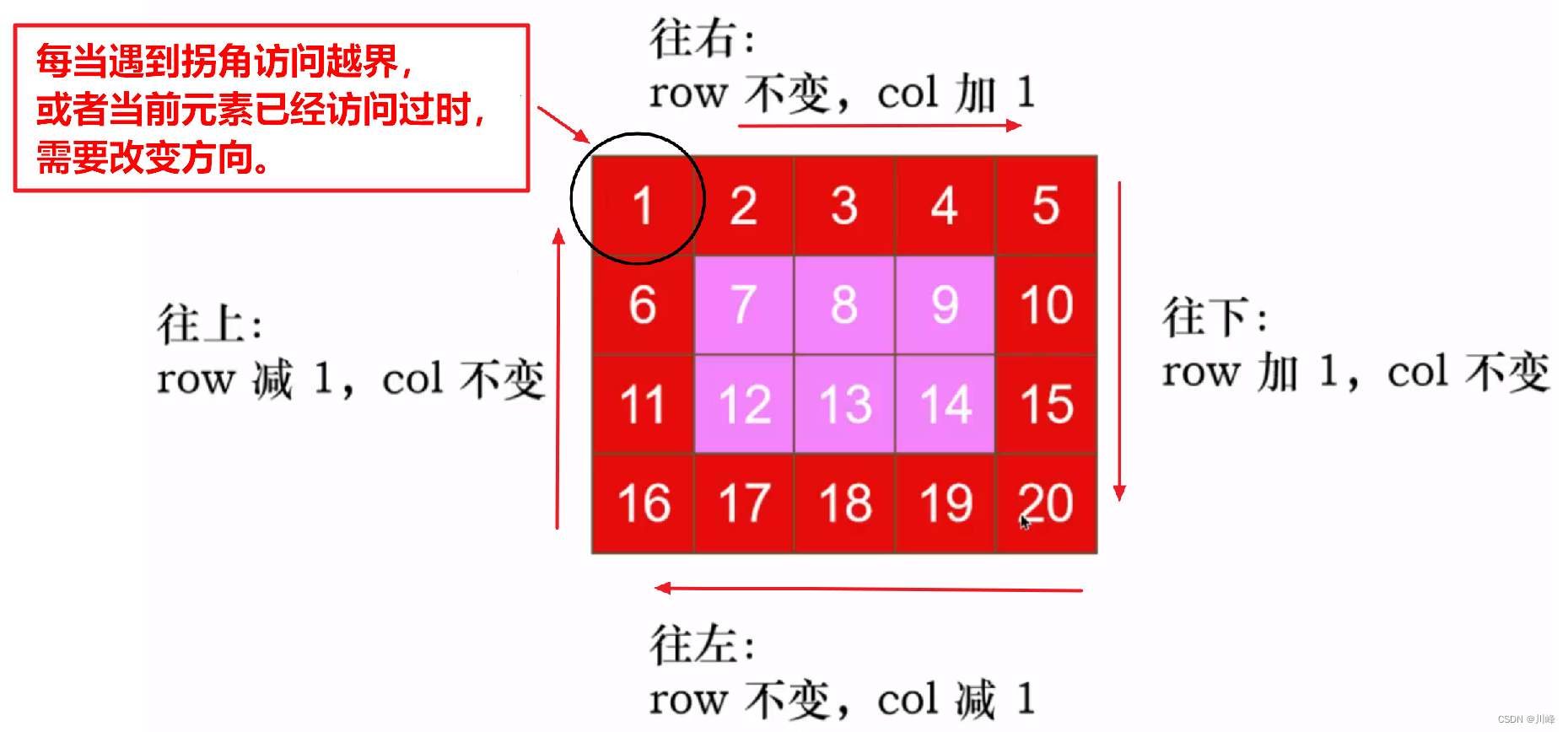
2） DFS 遍历： 从 （0,0） 出发，按 右、下、左、上 四个方向 DFS，定义二维方向数组 int [][] dirs = {{ 0 , 1 }, {1, 0}, {0, -1}, {-1, 0} } ，以及boolean[][] visited数组，每次 收集当前节点并 标记已访问 ，然后计算下一个节点 x + dirs[k][0], y + dirs[k][1] ，其中 k 表示方向，初始 k == 0 ，在每次递归中收集完节点后先判断下一个点 是否越界或者已访问 过，如果未越界且未访问，就进行递归调用，如果 越界或者已访问过，就改变方向 k = ( k + 1 ) % 4 ，然后再次重新计算下一个节点的值（注意点）。
可以采用循环（循环 M X N 次）或者dfs递归函数标准模板实现。

递归版本：

迭代版本：

59.螺旋矩阵 II

解题思路：

同54，先创建一个二维数组，将54题中获取matrix[x][y]值的地方换成给matrix[x][y]赋值即可

按环访问版本：

DFS递归版本：

DFS迭代版本：

73.矩阵置零

解题思路：

1）使用两个boolean数组 rows[M] 和 cols[N] 分别记录 每一行 和 每一列 是否需要置 0 ，
先遍历一遍矩阵如果 matrix[i][j] == 0 ，则记录 rows[i] = true 同时 cols[j] = true ，
最后再 遍历一遍矩阵，如果 rows[i] 或 cols[j] 为 true ，就将 matrix[i][j] 置 0 。
此方法空间复杂度为 O(m+n)

解题思路：

2) 利用原始矩阵的第 0 行和第 0 列来作为两个标记数组， 分别用来记录除了第一行和第一列之外的某一行某一列是否需要置 0。
需要预先使用 两个变量 来 标记第 0 行第 0 列中是否包含 0 ，
然后先遍历一遍矩阵， 从 [1,1] 位置开始处理， 如果 matrix[i][j] == 0 , 则更新 matrix[i][0] == 0（该行需要置 0） 以及 matrix[0][j] == 0（该列需要置0） ,
然后再遍历一遍矩阵 ，从 [1,1] 位置开始处理， 判断如果 matrix[i][0] == 0 或 matrix[0][j] == 0 ，则将 matrix[i][j] 置 0 。
最后处理完毕后再单独根据前面两个标记变量来处理第 0 行和第 0 列是否需要置 0 。

解题思路：

3）针对方法2的优化： 仍然利用原始矩阵的第 0 行和第 0 列， 然后只 使用一个变量来标记第 0 列是否需要置 0 即可，倒序从最后一行开始遍历除了第 0 列以外的每个元素并处理，这样避免第 0 行的元素被提前更新（第 0 行会被最后处理）。这种方法只是省了一个变量而已。

这道题的关键点是不能先对前面的位置进行置0处理，因为“将该行和该列全部置0”的行为会导致在后面位置的判断受到影响，如果后面的某个位置因为前面位置的判断处理预先置0了，后面再使用的时候就是被覆盖之后的值了，这样后面就无法做出准确的判断，很有可能出现矩阵全被置成0的情况。所以需要额外找一个地方来记录“某行某列是否需要置0”这样的标记，简单的想法就是方法1使用两个额外数组来记录（空间O(m+n)），精进一点的节约空间的想法就是利用原始矩阵的一部分来记录，即方法2和方法3（空间O(1)）。

289.生命游戏

解题思路：

由于矩阵中的每个元素的值只有 0 或者 1 ，因此可以 使用矩阵中每个元素的二进制位来表示复合状态，
使用整型32位二进制位中的低2位 00 ，其中 低位 用于表示 原始状态 ，高位 用于表示 修改后的状态 。
遍历一遍矩阵 ，求出每个位置周围 八个方向 上的 活细胞数量 （利用 dirs 数组技巧），然后根据题目规则修改每个元素的 低2位 二进制位中的 高位的值 。
如果需要将细胞 死亡 修改为 活细胞 的，则只需要进行 num | 10 操作即可将高位置为1，而需要将 活细胞 修改为死亡的可以 高位 不需要动（ 因为原始 值只有0或者1，只会用到低位，故高位默认是0，01或00 ）。
注意：判断原始状态时直接使用元素值，因为遍历矩阵的每个元素都是首次访问未被修改过，而修改则是修改 元素 的二进制位上的高位。但是在 计算当前 元素 周围八个方向上的活细胞数量时，应该用 num & 1 判断，也就是只看其 低位上的 原始状态 ，因为 八个方向上的 元素 有可能是被修改过的。
最后再次遍历一遍矩阵，将每个元素变成其低两位二进制位上 高位的值 即可（通过 >>1 操作）。

这道题与73题在思想上十分类似，那就是需要找一个地方先存储修改的状态值，完事之后再根据存储的状态标记来修改矩阵，而题目要求原地修改，那么只能在原始矩阵本身上做处理，本题是利用了元素值的空闲二进制位（题目元素只有1或0）。

48.旋转图像

解题思路：

1）同54螺旋矩阵的思想， 按层/环/圈访问 ，定义四个方向边界 T = 0, B = N - 1, L = 0，R = N - 1 ，
外层循环的条件是 L < R （或 T < B）, 在每一层循环中，分别交换位于四条边上的元素值，通过循环控制交换的次数为 R - L 或 B - T，交换完成后，外层向内缩小一圈，即 T++, B--, L++，R-- 。
注意：交换元素时， 按照 顺时针方向 交换，（按照顺序得先预留坑位，倒着进行）
最上边的 元素 值应该放到最右边 matrix[T][L+i] -> matrix[T+i][R]，
最右边的 元素值 应该放到最下边 matrix[T+i][R] -> matrix[B][R-i] ,
最下边的元素值 应该放到最左边 matrix[B][R-i] -> matrix[B-i][L]，
最左边的元素值应该放到最上边 matrix[B-i][L] -> matrix[T][L+i]

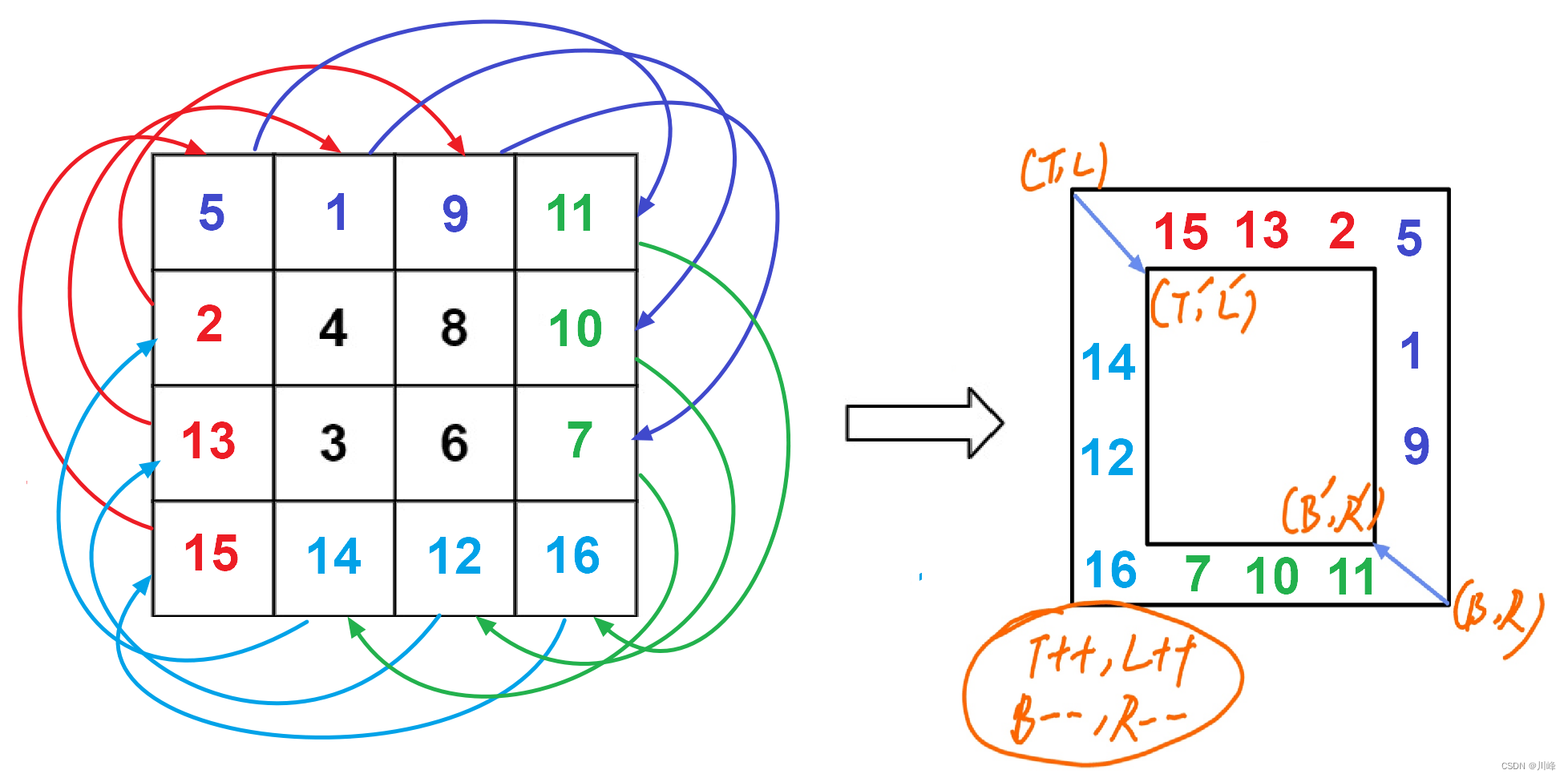
如上图所示，虽然交换是效果是顺时针的，但实际代码交换时，需要先记住其中一边，留出坑位，然后按逆时针的顺序往坑位方向填充。

注意上面代码中，while循环的退出条件是 L < R，但是与54题相比，不需要处理 L==R 的情况（或者T==B），这是因为本题输入的是一个 n x n 的正方形矩阵，这种矩阵的特点是：

1）要么最后 L==R 退出，此时中间还剩一个点，自然不用继续交换了，例如 3x3 的矩阵就是如此
2）要么最后 L > R 退出，此时矩阵中已经全部交换完毕，没有剩余的了，例如 4x4 的矩阵就是如此

解题思路：

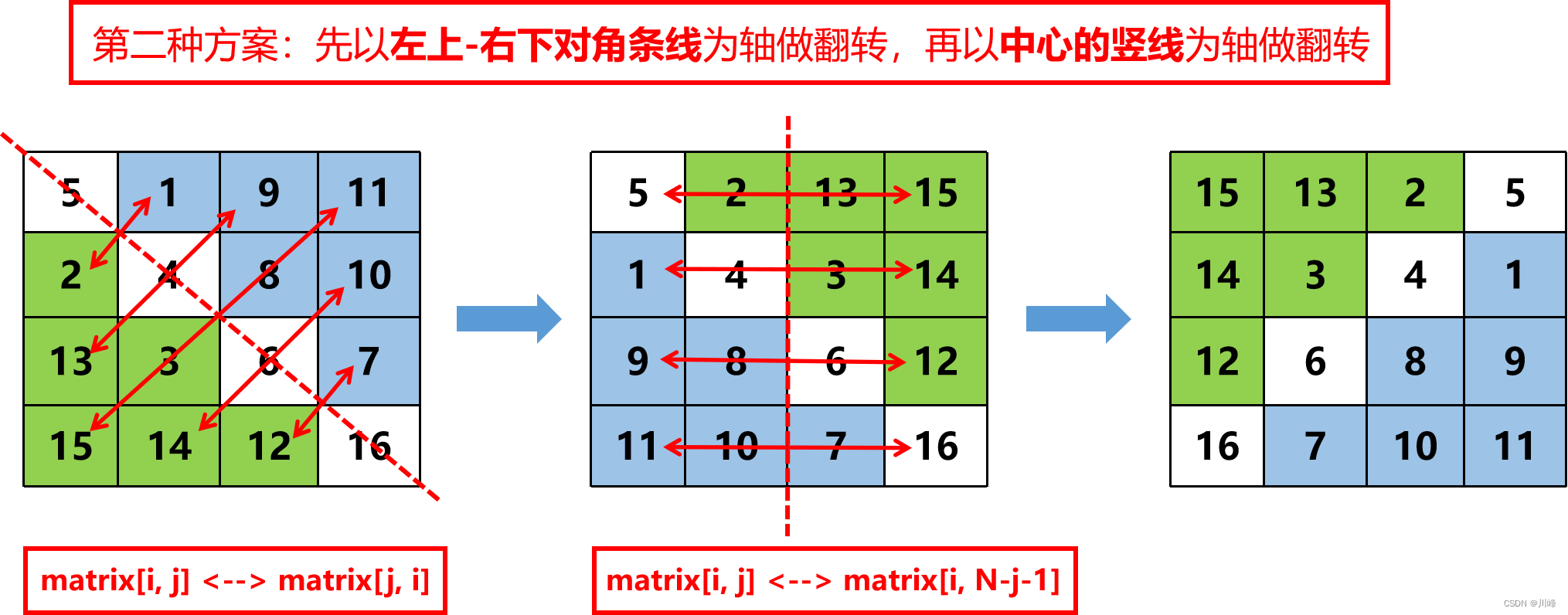
2）先沿着左对角线镜像翻转，再沿着中轴竖线左右镜像翻转，
对角线镜像翻转具体操作：遍历矩阵的左下半部分 i : [0, N)，j : [0, i) ，交换 matrix[i, j] 和 matrix[j, i] 即可。
左右镜像翻转具体操作：遍历矩阵的左边一半的列 i : [0, N)， j : [0, N / 2) ，交换 matrix[i , j] 和 matrix[i , N - j - 1] 即可。

解题思路：

3）先沿着中轴横线上下镜像翻转，再沿着左对角线镜像翻转，
上下镜像翻转具体操作：遍历矩阵的上边一半的行 i : [0, N / 2)， j : [0, N) ，交换 matrix[i, j] 和 matrix[N - i - 1, j] 即可。
对角线镜像翻转具体操作：遍历矩阵的左下半部分 i : [0, N)，j : [0, i) ，交换 matrix[i, j] 和 matrix[j, i] 即可。

本题其实通过左右镜像翻转 + 右对角线镜像翻转，或者 右对角线镜像翻转 + 上下镜像翻转也可以做到，通过观察就可以发现。但是右对角线在交换时坐标不如左对角线方便。

118.杨辉三角

解题思路：

将问题转化为 左对齐的二维数组 去思考，当前的值 = 上一行的值 + 左上的值
第 i 行中，第 0 列和最后 1 列为 1, 其它满足 res[i][j] = res[i - 1][j] + res[i - 1][j - 1]
按照遍历矩阵两层 for 循环的方式处理，矩阵的 行数 是题目给出的 N ，矩阵的 列数： 第 i 行有 i + 1 列 ，因此 j : [0, i] (i 从 0 开始)

如果觉得List麻烦，可以直接使用一个二维数组来计算，最后再转一下，不过同样麻烦：

119.杨辉三角 II

解题思路：

1) 同118，先生成 rowIndex + 1 行的杨辉三角数组，然后返回第 rowIndex 行即可

解题思路：

2) 使用 滚动数组 ，记住前一行，每次更新完当前行后，将当前行赋值给前一行

解题思路：

3) 使用一个数组， 每行中从右往左更新，从第 j = i 列开始倒序计算，res[j] = res[j] + res[j - 1]，初始 res[0] = 1

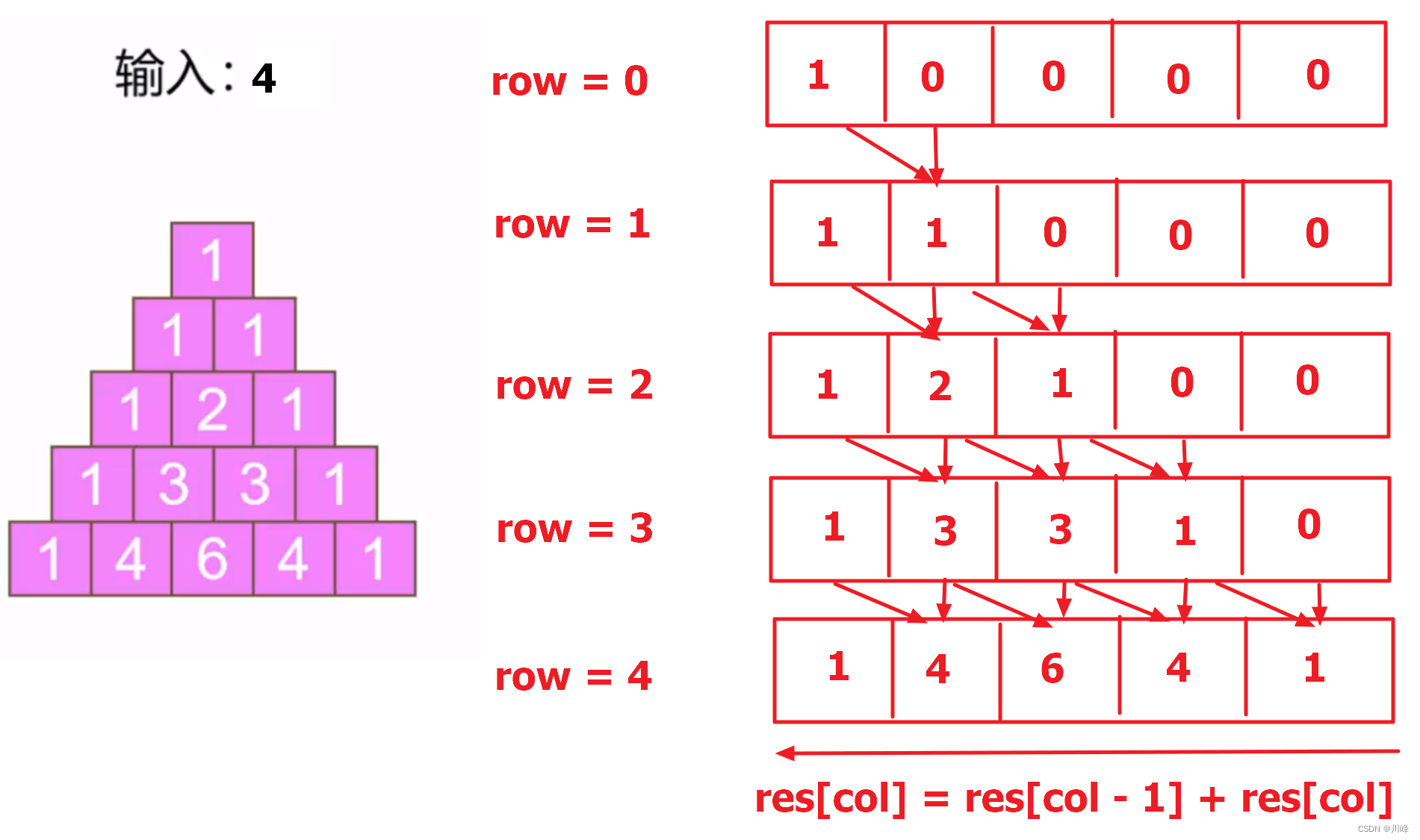
这个时候，当前行还没有更新时，把数组本身看成是上一行留下来的值，当前位置的值其实就是位于当前位置上一行的值，前一个位置的值其实就是位于上一行的前一个位置的值。

36.有效的数独

解题思路：

使用 3 个 boolean 标记数组，分别标记原数组 每一行、每一列、每一个 3x3 宫格中 1-9 是否出现
扫描二维数组的每一个数字，判断其在这 3 个标记数组中有没有出现过，如果已经出现过，说明违反了数独的规则，返回false；如果没有出现过，就将其在这 3 个标记数组中分别标记为true。
注意：在遍历矩阵时，跳过空格（即字符'.'），只处理数字字符。

对于每一行的数字1-9，定义如下：

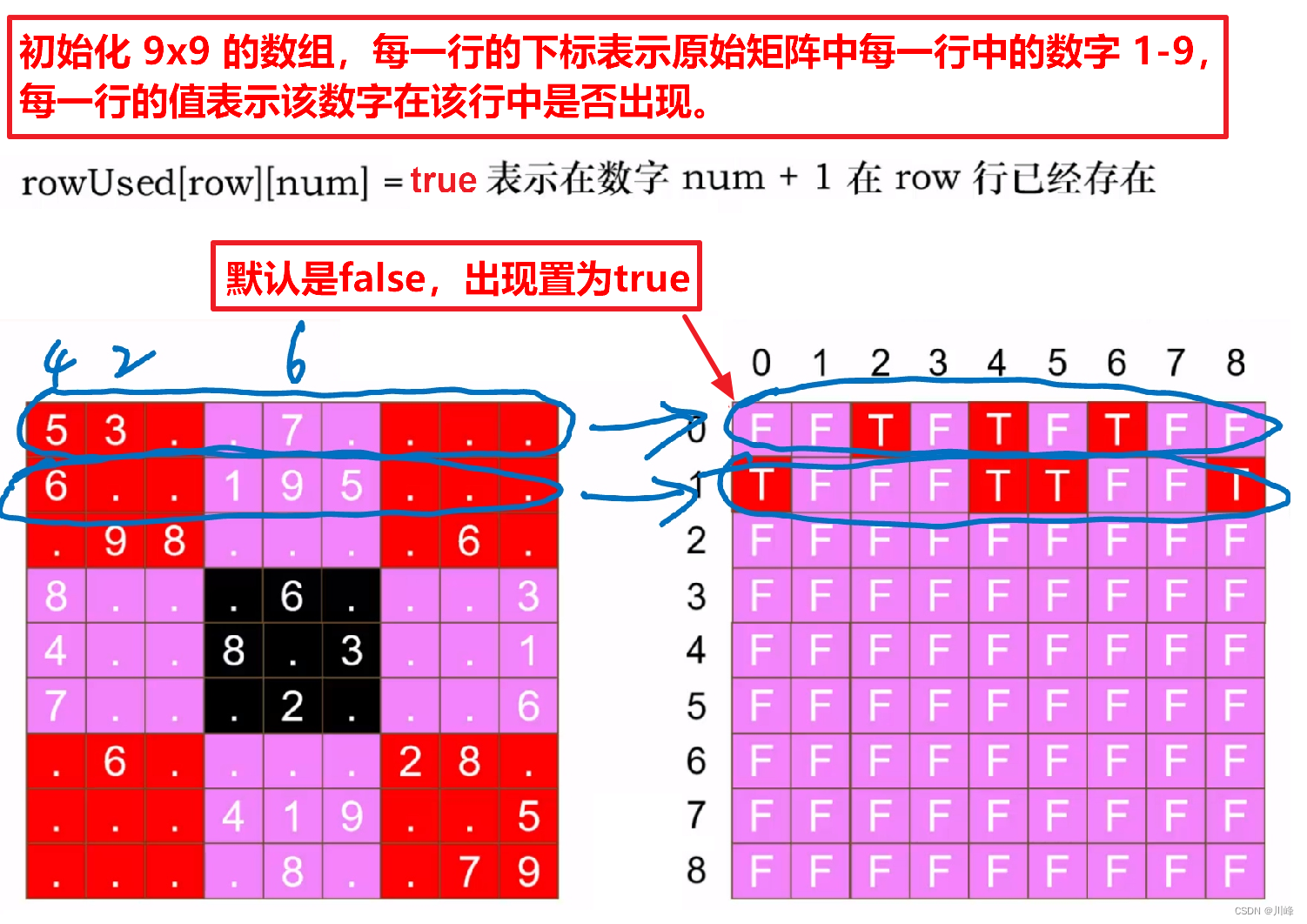
这里为什么是 9x9 的二维 boolean 数组呢，因为原始矩阵有 9 行，所以一维长度是 9，而每一行中我们要表示 1-9 共 9 个数字的存在状态，所以每一行中需要 9 个长度的数组。

对于列，是类似的表示方式：

对于 3x3 的小宫格，显然需要一个三维的 boolean[3][3][9] 数组。

251.展开二维向量

解题思路：

1）内部使用 list 来接收，使用 list.iterator() 对应方法，使用 iterator.next()、iterator.hasNext() ，代码略。

解题思路：

2） 双指针 使用两个变量 row 和 col 分别指向一维和二维的下标索引， 内层走到头了， row 换行下一层 col 从头开始走，跳过空行

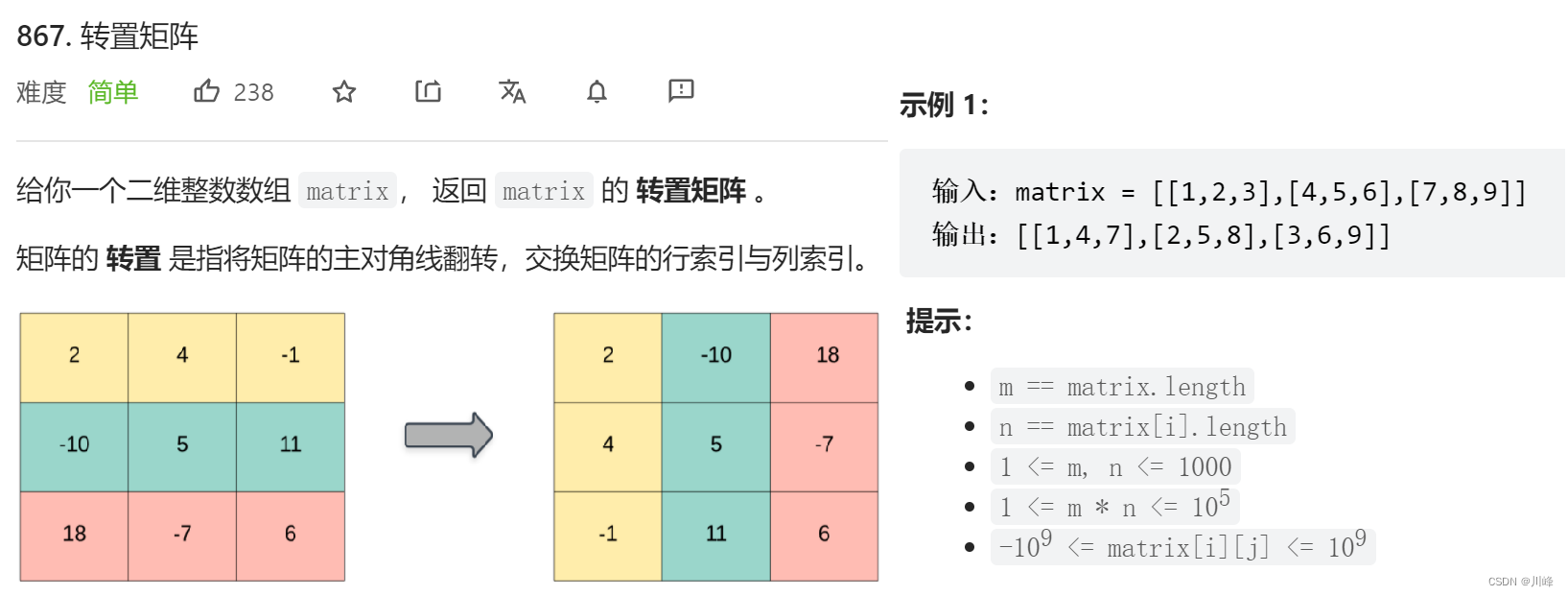
867.转置矩阵

解题思路：

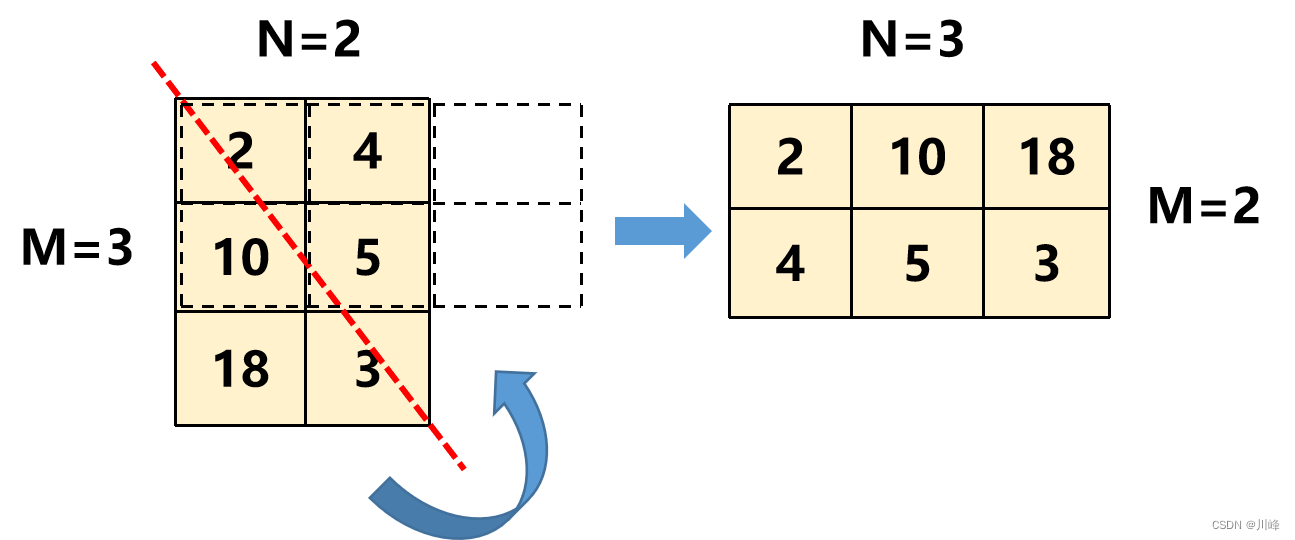
对于 M 行 N 列的矩阵，创建一个 N 行 M 列的数组res( 行数列数对调 )，然后遍历矩阵保存即可 res[j][i] = matrix[i][j] 保存时 行列坐标对调 即可
注意跟【48.旋转图像】的区别，旋转矩阵是顺时针旋转，本题只是沿着左上-右下对角线镜像翻转。

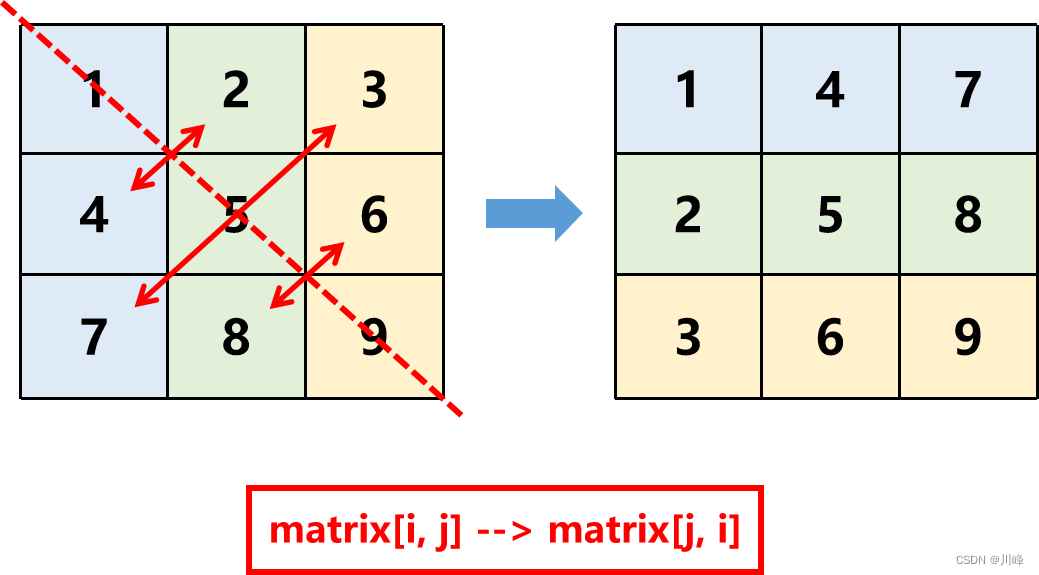
可以想象用手指捏住卡片的左下角，然后沿着左上-右下对角线向右上角方向翻转。

这里为什么结果数组是N行M列的呢，因为题目矩阵不一定是正方形的，例如下图 3x2 的矩阵，matrix[2][0] 翻转后应该存到 matrix[0][2]，如果结果数组行列不对调，显然存不下。

当然，也可以换一种写法，按照遍历结果矩阵的方式，对调下标到原始矩阵中取值：

304.二维区域和检索 - 矩阵不可变

解题思路：

1) 二维前缀和数组，利用求面积的思想，定义 S(i, j) 表示二维矩阵中以[0, 0]为左上角，[i, j]为右下角的矩形面积，
那么有 S(i, j) = S(i - 1, j) + S(i, j - 1) - S(i - 1, j - 1) + matrix[i][j]
因此 sumRegion(x1, y1, x2, y2) = S(x2, y2) - S(x1-1, y2) - S(x2, y1-1) + S(x1-1, y1-1)

二维前缀和数组中的每一个格子记录的是「以当前位置为区域的右下角，区域左上角恒定为原数组的左上角的区域和」如果觉得不清晰，请将将 S[i][j] 理解成是以 (i, j) 为右下角，(0, 0) 为左上角的区域和。

S[i, j] 的图示如下：

S[i - 1, j] 的图示如下：

S[i, j - 1] 的图示如下：

S[i - 1, j - 1] 的图示如下：

因此，合起来就是：

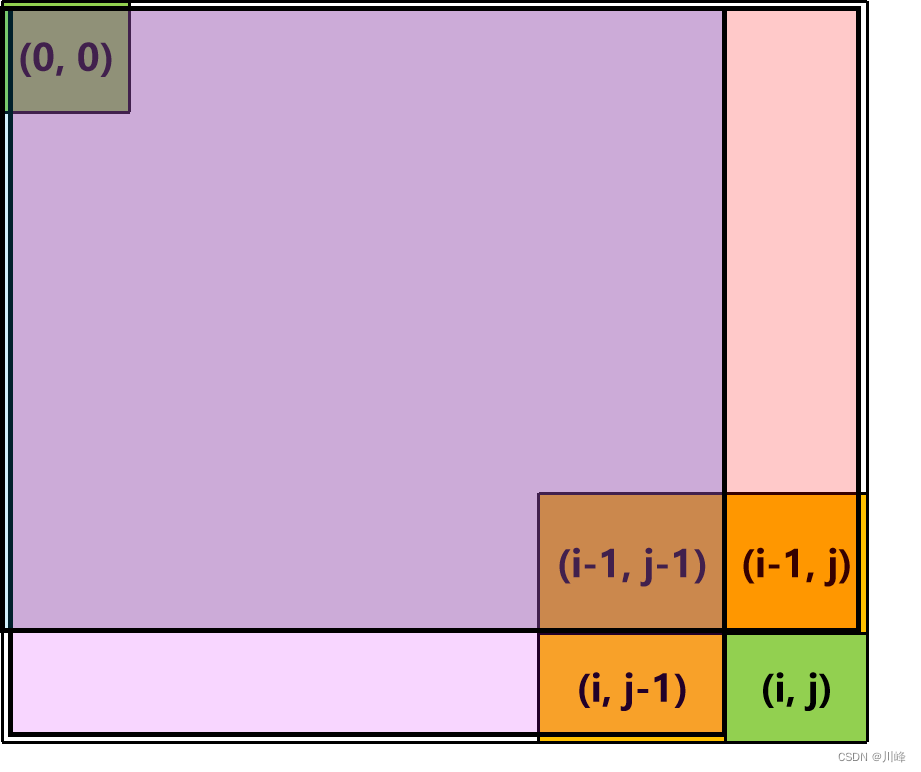
S[i, j] 等价于 S[i - 1, j] + S[i, j - 1] + matrix[i, j] 但是多重复加了一个S[i - 1, j - 1] ，因此需要减去一个S[i - 1, j - 1]

有了 S[i, j] 的计算公式，我们扫描一遍原始矩阵，对每个格子计算其 S[i, j] 的值，由此得到一个二维前缀和数组。当我们要求 (x1, y1) 作为左上角，(x2, y2) 作为右下角的区域和的时候，就可以直接利用前缀和数组快速求解：

[x1, y1] 到 [x2, y2] 区域的和就等价于以 [x2, y2] 为右下角的区域和减去上面躺着的以 [x1 - 1, y2] 为右下角的区域和，再减去左边站着的以 [x2, y1 - 1] 为右下角的区域和，但是多重复减了一个以 [x1 - 1, y1 - 1] 为右下角的区域和，因此还需要加上一个以 [x1 - 1, y1 - 1] 为右下角的区域和。

注意，为了方便计算处理边界条件，前缀和数组的长度各加了1，相当于在原始矩阵的左边和上边各加了一行值全为 0 的空行，这是防御编程的思想。此时 prefixSum[i][j] 的含义是表示原始矩阵中前 i 个行和前 j 个列（从1开始数）组成的二维区域累加和。也就是说prefixSum中的下标含义是个数，因此在计算sumRegion的时候，可以将参数索引下标转换成个数下标，这样就对上前面总结的计算公式了。

解题思路：

2) 求出每行的前缀和 ，将每一行求一个前缀和数组， M 行共有 M 个前缀和数组，在求 sumRegion 时，其实就是遍历 [ row1... row2] 的每一行，利用该行的前缀和数组之差求出该行的 [ col1...col2 ] 区间之和，然后将每行的结果累加起来即可。

这种思想比方法1要简单一些。（虽然方法1在求sumRegion时更高效）

308.二维区域和检索 - 可变

解题思路：

求出每行的前缀和，同304题方法2 ，利用前缀和的差值求区域和，只不过多了一个update方法，在更新时，我们只需要将前缀和数组中第 row 行的 col 列往后的每个前缀和的值加上当前更新的增量即可。

363. 矩形区域不超过 K 的最大数值和

解题思路：

二维数组压缩成一维数组 （数组压缩技巧）
外层 for 循环遍历 [0, M - 1] 的每一行，行下标记作 s ，每次创建一个与列数等长的一维数组 arr ，用于保存 [s..i] 行的压缩结果
内层循环每次选择当前 s 行作为 起始行 ，遍历 [s, M - 1] ，每次将当前第 i 行累加到 arr 中，那么此时 arr 中 只包含 s 行 ~ i 行 的元素累加和（即 s..i 行此时被压缩成了 一行）。 然后每次在这个 s..i 行压缩而成的 一维数组 arr 中，求 ≤ k 的子数组最大累加和即可。

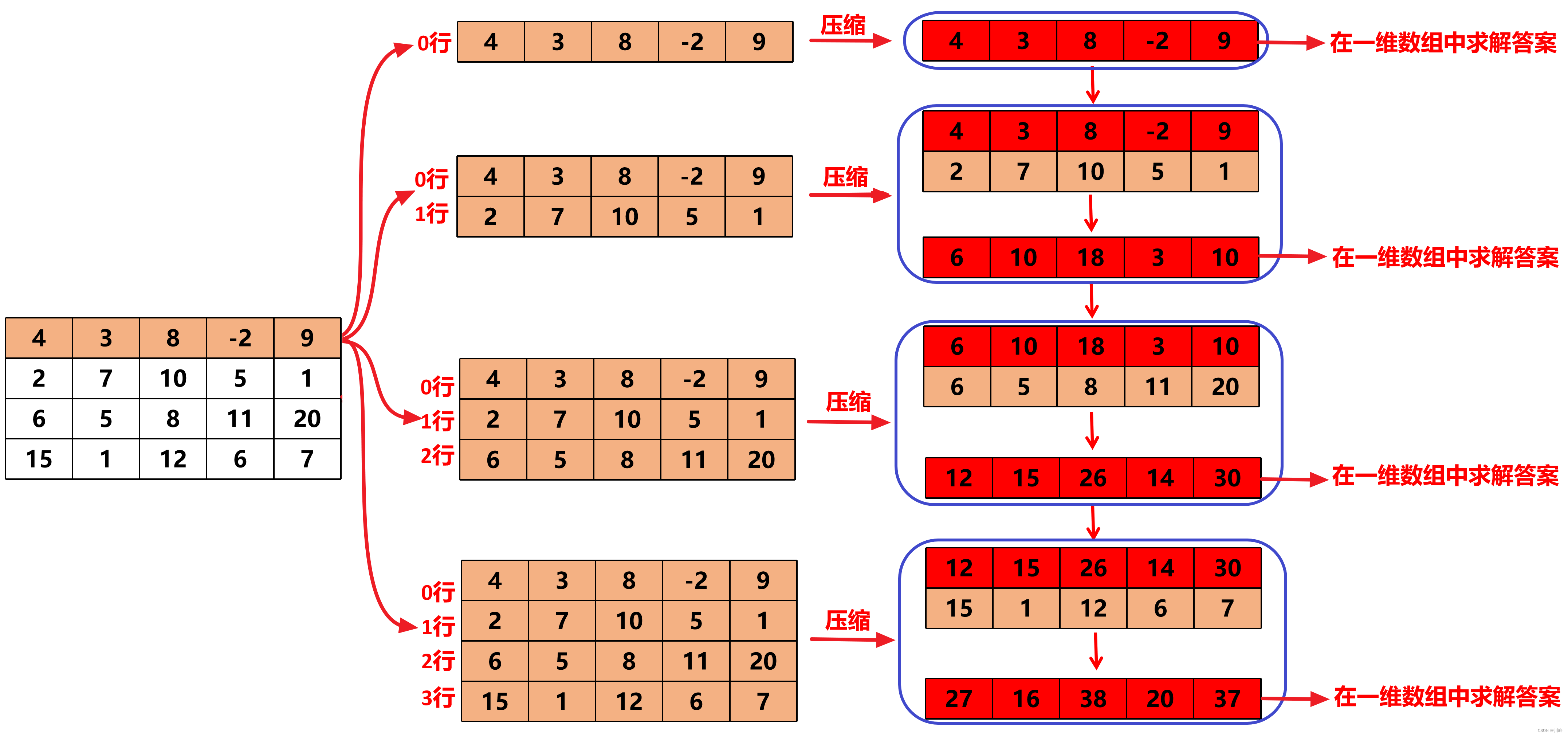
这个过程其实就是将从 0 行出发的、每次递增 1 行直至包括所有行在内的行压缩成了一行，在压缩行中求解：

这样从 0 行出发的所有矩形区域都会被扫过，不会有遗漏。

对于从 1 行出发、从 2 行出发、从 3 行出发的处理雷同，都是每次压缩再求解：

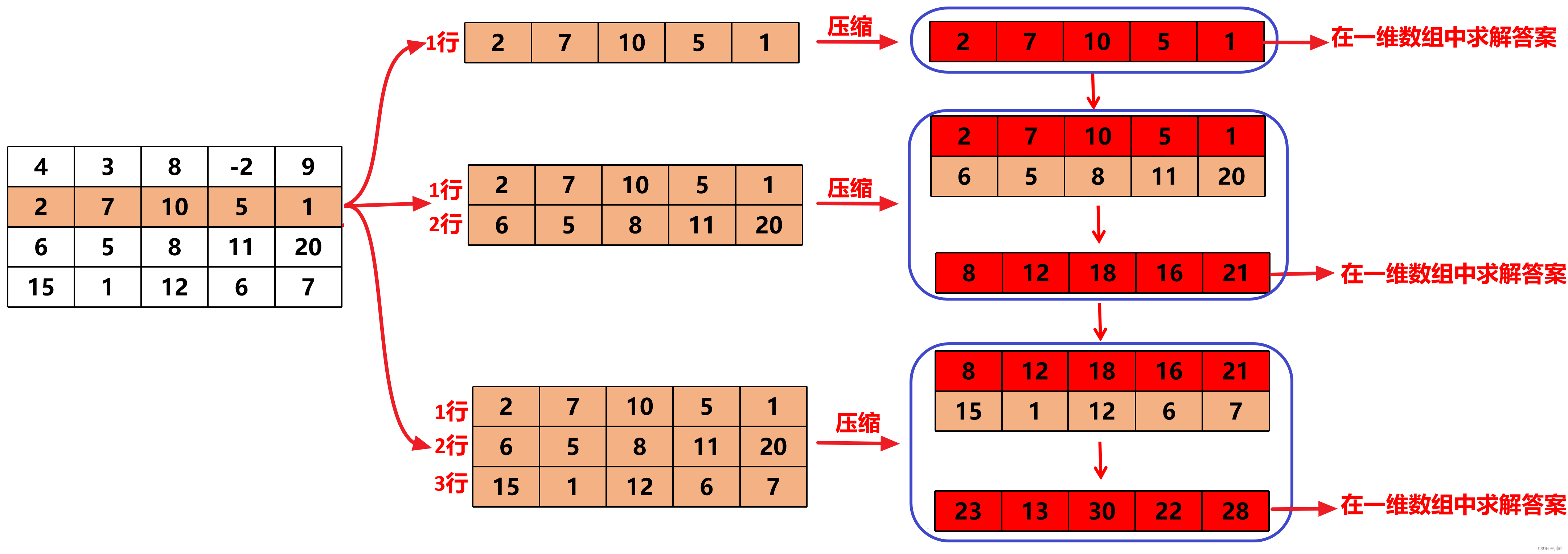
通过以上过程我们可以先写出主流程代码：

现在，我们只剩下最后一个问题，那就是如何实现上面代码中的 getMaxNearK() 方法

在 一维数组arr 中求 ≤ k 的子数组最大累加和 ， 有以下几种方法：

1）可以通过 暴力 方法求 前缀累加和 ：

① 先计算一下一维数组中 累加和 的最大值 max ，如何 max 不超过 k , 直接返回 max 就可以了，不用继续找了。
② 否则就 双层for循环 暴力计算每一个子区间的累加和，外层枚举 i : [0, N - 1] 每一个 i 做开头，内层枚举 j : [i, N - 1] 每一个 j 做结尾，内层循环中不断累加 arr[j] 到 sum 中，因为 j 是从 i 开始枚举的，所以每次更新 sum 时，我们就得了一个 [i...j] 区间的累加和，这时我们判断如果 满足 sum ≤ k ，就记录最大值即可。

实现代码：

再稍微解释一下上面代码中第一个 for 循环里，当 sum <= 0 时，为什么要重新从当前数字开始累加：因为如果 sum 是负数，【继续累加当前数字】不会比【只使用当前数字自身作为累加和】收益更大（这里有一点贪心思想）。例如 sum = -10，arr[i] = -5，如果继续累加，收益不增反降。再例如 sum = -10，arr[i] = 12，如果累加得到的是 2，但是不累加直接取 arr[i] 得到的是 12。

2）求解子数组累加和的经典做法是利用前缀和数组之差，因此我们可以先对arr计算出前缀和数组，然后双重for循环枚举每一种前缀和数组的子区间，外层枚举 i: [0, N - 1]，内层枚举 j: [0, i]，利用 prefixSum[i + 1] - prefixSum[j] 就能得到区间 [i...j] 的累加和，判断是否 ≤ k 即可。

实现代码：

3）用有序表 TreeSet 代替前缀和数组，只需 一层for循环 ，每次将当前更新的累加和 sum 添加到有序表中，在有序表中寻找 ≥ sum - k 的最小值 find ，如果这个值存在，就记录 sum - find 的最大值即是所求 。

实现代码：

注意：有序表TreeSet中，TreeSet.ceiling(x) 返回 >=x 且最接近 x 的最小值！floor(x) 返回 <=x 且最接近 x 的最大值！

解释一下，上面为什么要查找的是 TreeSet.ceiling(sum - k) ，理解这个我们需要先明白 TreeSet 中存储的是什么，TreeSet 其实就相当于是上面方法 2）中的前缀和数组 prefixSum，其中保存的每一个元素就是 prefixSum 中的值。这样，我们把当前正在累加的 sum 看成是 prefixSum[i + 1]，我们要求的就是 prefixSum[i + 1] - prefixSum[j] ≤ k，这个不等式换算一下就是 prefixSum[j] ≥ prefixSum[i + 1] - k，因此也就是说在 TreeSet 中找一个数，它 ≥ sum - k 。可参考下图理解：

因此，可以认为方法 3）本质上其实跟方法 2）是等价的，只不过是利用了 TreeSet 这种高级的数据结构（红黑树）的一些便捷查找 Api 简化了方法 2）中的双层 for 循环查找，提高了查找效率而已。

本题方法计算一维数组中 ≤ k 的子数组最大累加和的三种方法中，我认为方法 2）是最好理解的，而方法 3）是方法 2）的精进版本，但是由于题目的数据量不大，方法 1）的暴力方式反而是最高效的（在LeetCode上提交的Java版本中耗时最少），在数据量较大的时候，方法 3）会更加高效一点。

本题最少时间复杂度可以达到 O(N^3)，如果用暴力可能需要 O(N＾6)。（因为找子矩阵需要 O(N＾4)找到再遍历求和是 O(N＾2)）

与本题类似的一道面试题：

给定一个整型的二维矩阵，返回子矩阵的最大累加和。

解题思路：这个问法比原题更简单了，没有 ≤ k 的限制，主要思路跟上面一样，我们直接边压缩边计算累加和的最大值即可，不需要单独再计算 ≤ k 的最大累加和了。

实现代码如下：

这里 sum < 0 时将 sum 清 0，也是为了保持累加和的最大收益，因为一个负数继续累加某个数字得到的累加和收益，不会比只取该数字本身作累加和的收益更大（贪心）。具体例子在前面计算一维数组中 ≤ k 的子数组最大累加和的三种方法中的方法1）里列举过了，可以翻上去看看。

348.设计井字棋

解题思路：

用 3个二维数组 分别记录玩家X在 每一行上、每一列上、每一条对角线上 分别放置的 棋子数量 ，每次move方法中，将当前玩家对应的 3 个数组中的 计数 + 1，如果某个数组中计数达到 N ，则该玩家获胜，返回该玩家序号即可。
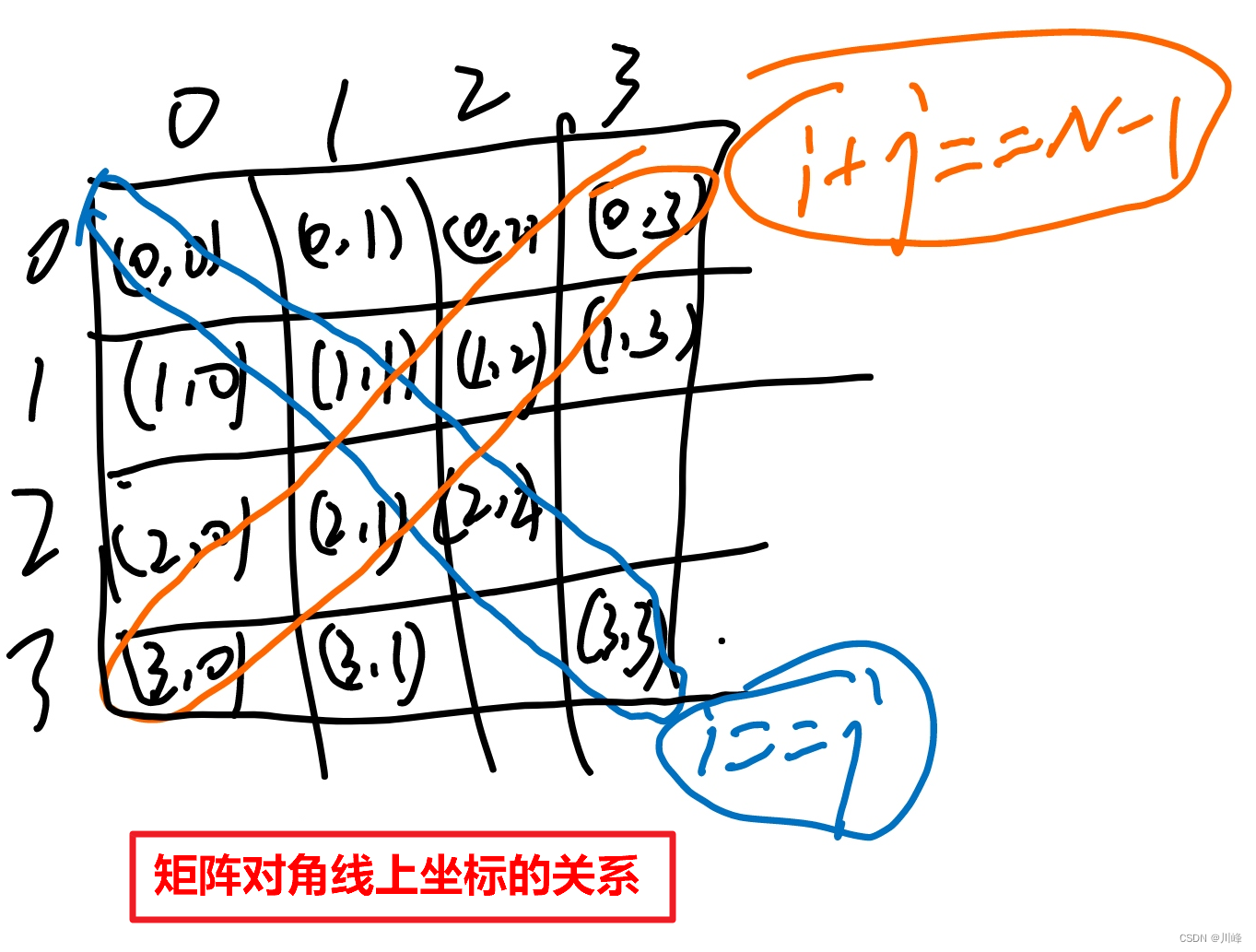
技巧： NXN 的矩阵中， 坐标点满足 i == j 的点位于 主对角线（左上-右下）， 坐标点满足 i + j == N - 1 的点位于次对角线（右上-左下）

296. 最佳的碰头地点

解题思路：

1. 排序 + 中位数 ， 曼哈顿距离其实是 两个独立变量的子问题的和 。 因此我们只要解决 一维 的情况，我们就可以把 二维 的情况当做 两个一维独立的子问题的和 。
中位数是最优的相遇点 。只要相遇点 左边和右边有 相同数目的点 ， 总距离都是最小的 。
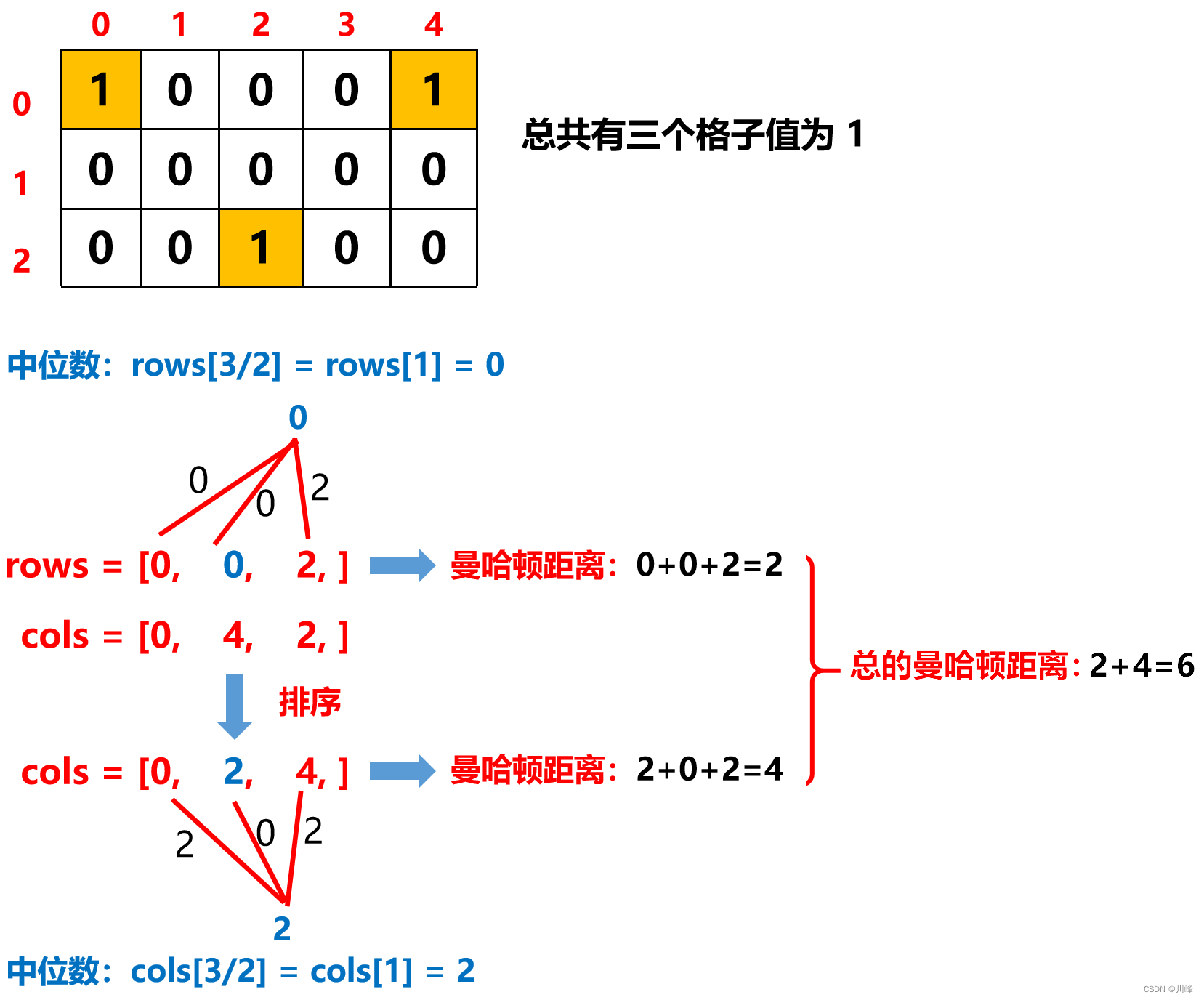
首先，我们遍历原始矩阵，只处理值为 1 的格子， 将每一个格子的行坐标和列坐标分别收集到 一维数组 中并排序 ，然后分别选择它们 中间的元素 ， 计算出两个独立的一维数组的曼哈顿距离，二者之和就是答案。

时间复杂度O(mnlogmn)

解题思路：

2. 按顺序收集坐标 + 中位数 ，同方法1，只不过在收集每个值为 1 的格子的 列下标 时，我们可以按照 先遍历列，再遍历行 的方式来收集，这样收集到的 列下标 就是已经 按顺序排序好的，从而省去排序操作的时间复杂度。 时间复杂度为 O(mn)。

解题思路：

3. 按顺序收集坐标 + 对撞指针 ， 同方法2，只不过在计算一维数组的曼哈顿距离时，不再需要知道中位数，只需要设置一对 对撞指针 L 和 R ，让 L 和 R 从数组的两端往中间逼近，不断累加位于两端的数字差值 points[R] - points[L] 即可。