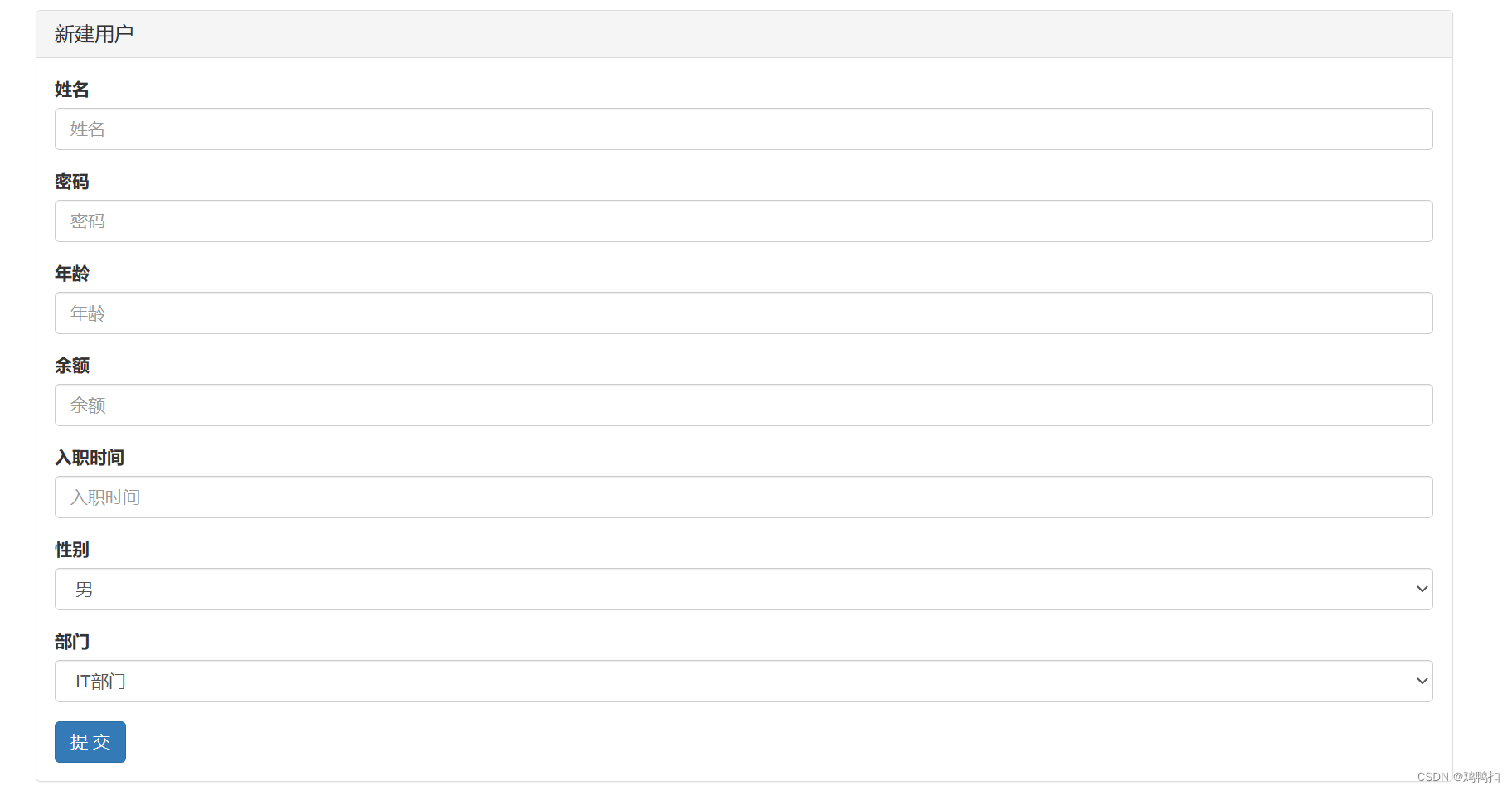
总述

• 无论使用什么格式的机器码来表示真值，若取一定位数n以后，各个比特位的排列个数是一定的，为$2^n$种排列，所以选择什么格式的机器码实质上选择什么映射方式来完成从这$2^n$种离散排列到离散的整数真值的映射，而不同的映射方式其实只是在：算数运算能力、逻辑比较能力和可读性三者中进行权衡。
• 需要解释上图，需要读者先接受一种思考的角度：比特位的排列可以暂时完全看成看成无符号数，其绝对值从左到右递增，而与具体的机器数格式无关

---

原码

最符合人类直觉的机器码

算数运算能力：差

• 符号位不能参与运算，需要另外设置电路进行处理
• +0和-0分别占了一个排列，既不统一又浪费空间

逻辑比较能力：差

• 需要先区分符号位，且在同一符号内部的变化趋势也不同，正数内部随着比特位的绝对值增大而增大，负数内部随着比特位的绝对值增大而减小。这意味着不仅要设置电路区分正负，甚至正数和负数内部的比较逻辑都需要不同的电路

可读性：好

• 可读性很好，可以很方便看出真值

---

反码

后面补码的出现，让反码成为了仅仅为了导出补码的工具

算数运算能力：差

• 符号位不能参与运算，需要另外设置电路进行处理
• +0和-0分别占了一个排列，既不统一又浪费空间

逻辑比较能力：一般

• 只需要区分符号位，在同一符号内部的变化趋势相同，都是随着比特位的绝对值增大而增大

可读性：一般

• 可读性一般，不容易看出真值

---

补码

补码继承了反码的优点，克服了反码的缺点。已经是一种很优秀的机器码了

算数运算：非常好

• 符号位可以直接参与运算
• 0的表示完成了统一，而且可以多表示一个最小值，一举两得

逻辑比较：一般

• 同反码一样，只需要区分符号位，在同一符号内部的变化趋势相同，都是随着比特位的绝对值增大而增大

可读性：差

• 基本上无法读了

---

移码

虽然补码对于机器而言已经近乎完美，但是在某些需要频繁比较而几乎不需要进行加减运算的场合，补码的表现依然可以改进，因为它每次比较都需要先判断符号位然后再比较。如果能想到一个能免去比较符号这一步的机器码就能解决这个问题，而移码恰好完美符合这一点。

算数运算：一般

• 不如补码方便，尤其是减法运算

逻辑比较：非常好

• 逻辑比较：只需要按无符号数的视角比较绝对值即可，绝对值越大所表示的数的真值就越大。不需要额外设置任何电路

可读性：很好

• 可读性：可以根据移码快速读出两数谁大谁小

---

IEEE 754阶码（本质是经过改造的特殊移码）

IEEE 754的阶码虽然本质上是移码，但是和一般的移码有所不同

• 先说明，改造了哪些地方：
  • 全0和全1机器码不能再用作普通阶码，要作特殊解释
  • 偏置值小了1
• 然后说明，为什么要这么改：
  • 全0和全1意义的修改是为了——需要特殊值来表示无穷大∞和非数NAN
  • 偏置值小1是为了——获得更大的正数阶码
• 结果：在这两点改动之后，阶码可以表示的真值的范围发生的变化是：
  • 最大值无变化，依然为$2^{n-1}-1$，最小值从$-2^n$变成$-2^n+2$