pytorch简介

为什么神经网络要自定义数据类型torch.tensor?
tensor可以放在gpu上训练,支持自动求导,方便快速训练,同时支持numpy的运算,是加强版,numpy不支持这些
为什么要求导?
导数是真实值和预测值的误差函数下降最快的地方,根据求导可以快速降低误差值,让真实值和预测值贴合

神经网络基础

监督学习:已经打标记的样本进行训练,然后预测
非监督学习:对一些无标记数据进行结构化分类,发现潜在的规律
强化学习:一个机器不断根据新的输入做出决策,然后根据结果进行奖惩来学习
线性模型:y=wx+b,w就是要优化的值,我们要根据损失值来不断优化w让他的预测贴近真实值
这需要知道loss函数,(真实值和预测值之间的误差),然后根据loss函数的反馈优化w降低loss
当loss求和最小的时候可以得出预测越来越准
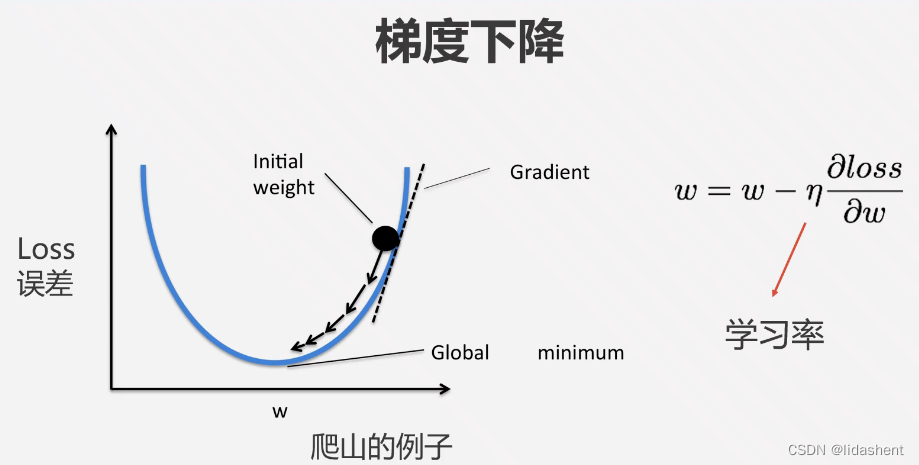
为了减少loss就需要知道loss在哪个方向下降的最快,这就是求导,梯度下降算法

更直观一点是让loss下降的更快,以至于降到最低,让真实值和预测值无限贴合,
学习率代表了斜率变化的步长,合理的设置会方便于我们找到最优w,错误的设置过大过小会导致预测值无法贴合真实值
在三维和多维度图象上更容易理解这一点

当有三个维度的数据时更加直观

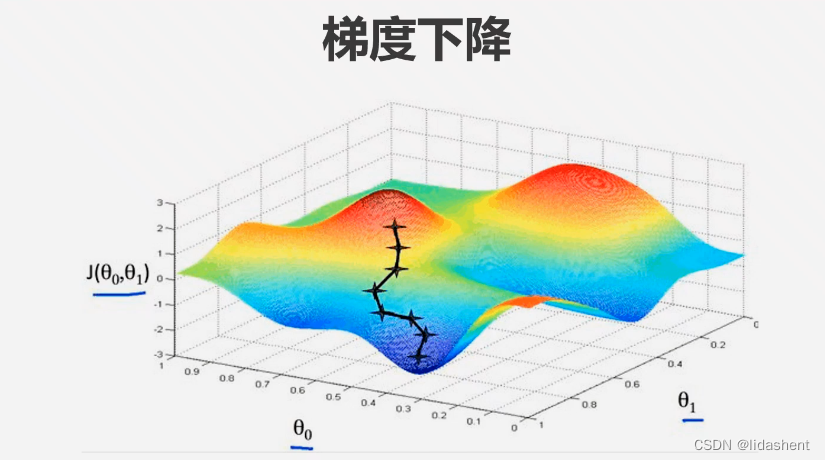
那么构建模型流程如下
定义参数,定义损失函数,定义网络模型,这里为线性模型,然后根据损失函数优化参数w让线性模型拟合的更好
理解线性模型对未来的深层模型构建有很大帮助
我们定义一些点,然后用线性模型拟合这些数据

x_train	np.array([[3.3],[4.4],[5.5],[6.71],[6.93],[4.168],[9.779],[6.182],[7.59],[2.167],[7.042],[10.791],[5.313],[7.997],[3.1]],dtype=np.float32)
y_train	=np.array([[1.7],[2.76],[2.09],[3.19],[1.694],[1.573],[3.366],[2.596],[2.53],[1.221],[2.827],[3.465],[1.65],[2.904],[1.3]],dtype=np.float32)

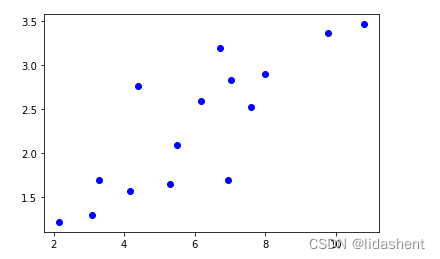
然后将这些数据转化为tensor类型,定义参数wb,使用正态分布随机初始化数据wb,定义网络模型,损失函数模型
损失函数模型计算误差方式为求平方差之和

x_train	=torch.from_numpy(x_train)
y_train	=torch.from_numpy(y_train)
w1=Variable(torch.randn(1),requires_grad=True)
b1=Variable(torch.zeros(1),requires_grad=True)
def linear_model(x):
    return x*w1+b1
def get_loss(y_,y):
    return torch.mean((y_-y_train)**2)
y_=linear_model(x_train)
loss=get_loss(y_,y_train)

画出初始化后的预测图形为:这肯定不对的,然后对其进行优化

plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'bo', label='real')
plt.plot(x_train.data.numpy(), y_.data.numpy(), 'ro', label='estimated')
plt.legend()

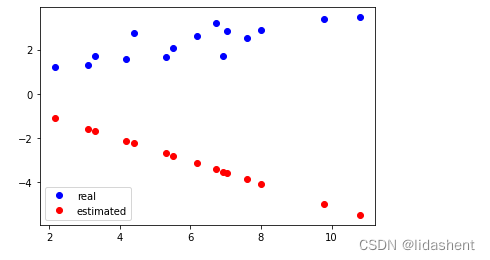
进行10次迭代
获得预测值,计算误差,将之前的梯度归零,计算新的梯度,根据新的梯度对参数wb进行优化

for e in range(10): # 进行 10 次更新
    y_ = linear_model(x_train)
    loss = get_loss(y_, y_train)
    
    w.grad.zero_() # 记得归零梯度
    b.grad.zero_() # 记得归零梯度
    loss.backward()
    
    w.data = w.data - 1e-2 * w.grad.data # 更新 w
    b.data = b.data - 1e-2 * b.grad.data # 更新 b 
    print('epoch: {}, loss: {}'.format(e, loss.data[0]))

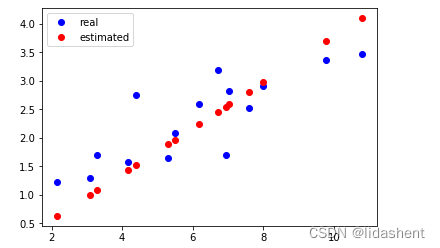
使用的是科学计数法,1e相当于10,科学记数法以x*10^n将所有数据进行分解,1e-2就是10的负二次方.0.01
梯度归零的意义在于得到新的梯度前清空上一次计算的梯度,对新的梯度进行优化
然而实际上,参数点往往分布的并不规律,也不可能仅仅用wx+b就可以拟合,
我们来设计一个新的图像
y = x+x2+x3+b

# 画出这个函数的曲线
x_sample = np.arange(-3, 3.1, 0.1)
y_sample = b_target[0] + w_target[0] * x_sample + w_target[1] * x_sample ** 2 + w_target[2] * x_sample ** 3
plt.plot(x_sample, y_sample, label='real curve')
plt.legend()

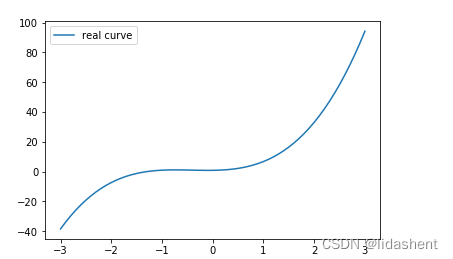
然后设置一些训练数据x和y
x为一个多行3列矩阵

x_train = np.stack([x_sample ** i for i in range(1, 4)], axis=1)
x_train = torch.from_numpy(x_train).float() # 转换成 float tensor
y_train = torch.from_numpy(y_sample).float().unsqueeze(1) # 转化成 float tensor 

定义wb参数和神经网络模型,这里依旧为线性模型,损失函数,损失函数同wx+b模型依旧求平常差之和

# 定义参数和模型
w = Variable(torch.randn(3, 1), requires_grad=True)
b = Variable(torch.zeros(1), requires_grad=True)
# 将 x 和 y 转换成 Variable
x_train = Variable(x_train)
y_train = Variable(y_train)
def multi_linear(x):
    return torch.mm(x, w) + b

查看原始拟合图像

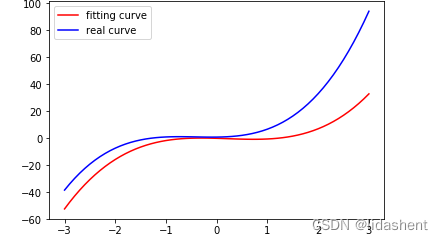
更新参数wb

# 进行 100 次参数更新
for e in range(100):
    y_pred = multi_linear(x_train)
    loss = get_loss(y_pred, y_train)
    w.grad.data.zero_()
    b.grad.data.zero_()
    loss.backward()
    w.data = w.data - 0.001 * w.grad.data
    b.data = b.data - 0.001 * b.grad.data

# 画出更新之后的结果
y_pred = multi_linear(x_train)

plt.plot(x_train.data.numpy()[:, 0], y_pred.data.numpy(), label='fitting curve', color='r')
plt.plot(x_train.data.numpy()[:, 0], y_sample, label='real curve', color='b')
plt.legend()

画出拟合后的图形

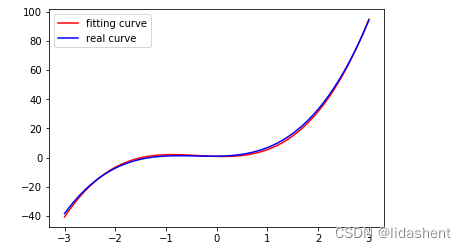
w	=	Variable(torch.randn(3,	1),	requires_grad=True)

设置自变张量不可缺少
varable在pytorch0.4之后就不再使用,以后的torch自带梯度计算
上面是单w权重的情况,实际使用中往往是多权重,会有w1,2,3
但是写法不变

plt.plot(x_train.data.numpy()[:,	0],	y_pred.data.numpy(),	label='fitting	curve',
color='r')

x_train.data.numpy()[:, 0]代表x_train所有行的第一个值x值
可以看到,对于线性模型只要模型设置正确,loss函数设置合理,就能够得到贴近值,这对于线性模型求解益处巨大,
然而有一类问题是线性问题不涉及的,那就是离散问题,无法用公式描述

分类问题分析:逻辑回归模型

他和上面的模型的区别在于多了一个sigmod函数,分类函数

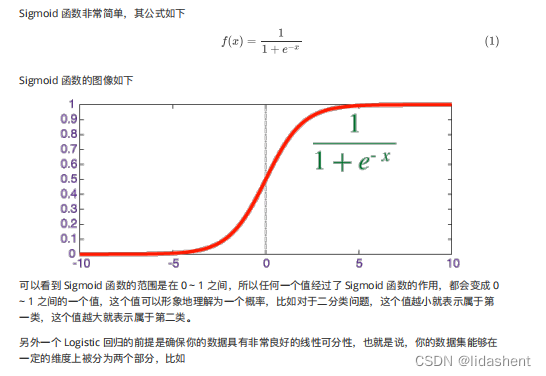
所有的y值都能够被放在-1到1的区间,这意味着可以把它看做概率,
分类问题和回归问题的区别在于回归问题是连续问题,比如拟合曲线,分类是离散问题,在解决问题前需要明白要解决的是那种问题

loss函数的变化:
既然是分类,输入任意数据经过sigmoid,a类概率为y_,b类概率为1-y_,如果输入的数据类型为a,则y_越大越好,1-y_越小越好
y_是概率值<=1
loss=-(y*log(y_)+(1-y)*log(1-y_))
输入的y只能为0,1
当输入0,0的概率损失函数loss=-(log(1-y_)).表示预测为假越大越好
当输入1,1的概率损失函数为loss=-(log(y_)),表示预测为真越大越好
当然log是有底数的,它的底数是e

逻辑回归实现

我们观察这些点的分布

# 从 data.txt 中读入点
with open('./data.txt', 'r') as f:
    data_list = [i.split('\n')[0].split(',') for i in f.readlines()]
    data = [(float(i[0]), float(i[1]), float(i[2])) for i in data_list]

# 标准化
x0_max = max([i[0] for i in data])
x1_max = max([i[1] for i in data])
data = [(i[0]/x0_max, i[1]/x1_max, i[2]) for i in data]

x0 = list(filter(lambda x: x[-1] == 0.0, data)) # 选择第一类的点
x1 = list(filter(lambda x: x[-1] == 1.0, data)) # 选择第二类的点

plot_x0 = [i[0] for i in x0]
plot_y0 = [i[1] for i in x0]
plot_x1 = [i[0] for i in x1]
plot_y1 = [i[1] for i in x1]

plt.plot(plot_x0, plot_y0, 'ro', label='x_0')
plt.plot(plot_x1, plot_y1, 'bo', label='x_1')
plt.legend(loc='best')

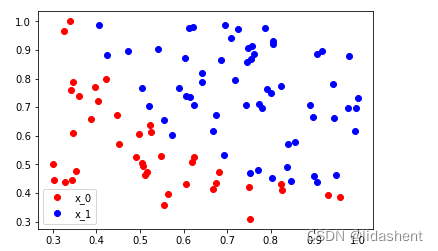
分布离散问题,使用逻辑回归来进行分类较为合适

torch.manual_seed(2000)

随机数种子,用于初始化模型参数,划分数据集,打乱数据等,有了初始值,则可以确保不同机器上,不同执行次数上模型初始化,数据初始化一致,实验结果具备可重复性

x0=list(filter(lambda x:x[-1] ==0.0,data))

filter传入一个lambda表达式,可迭代对象,返回一个迭代器,list将迭代器转化为list对象
对data中的行x进行迭代,找到每行最后元素等于0.0的行

plt.plot(plot_x1,plot_y1,"bo",label="x_1")

在坐标轴上画图,参数分别为x,y,颜色,标签
颜色ro红色,bo蓝色

plt.legend(loc='best')

选择最佳位置放置图像
那么延续之前线性模型的经验,我们需要设置wb,设置损失函数(这里不再求平方差而是求log),神经网络模型
对于sigmoid函数,
pytroch已经内置了这个函数,而且实现的速度更快,底层用c++编写,同时还有其他函数,直接调用即可
因此初始化wb和loss函数

np_data = np.array(data, dtype='float32') # 转换成 numpy array
x_data = torch.from_numpy(np_data[:, 0:2]) #  转换成 Tensor,大小是 [100, 2]
y_data = torch.from_numpy(np_data[:, -1]).unsqueeze(1) # 转换成 Tensor，大小是 [100, 1]
w = Variable(torch.randn(2, 1), requires_grad=True) 
b = Variable(torch.zeros(1), requires_grad=True)
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
def binary_loss(y_pred, y):
    logits = (y * y_pred.clamp(1e-12).log() + (1 - y) * (1 - y_pred).clamp(1e-12).log()).mean()
    return -logits
def logistic_regression(x):
    return F.sigmoid(torch.mm(x, w) + b)

将图像绘画出来如下

# 画出参数更新之前的结果
w0 = w[0].data[0]
w1 = w[1].data[0]
b0 = b.data[0]

plot_x = np.arange(0.2, 1, 0.01)
plot_y = (-w0 * plot_x - b0) / w1

plt.plot(plot_x, plot_y, 'g', label='cutting line')
plt.plot(plot_x0, plot_y0, 'ro', label='x_0')
plt.plot(plot_x1, plot_y1, 'bo', label='x_1')
plt.legend(loc='best')

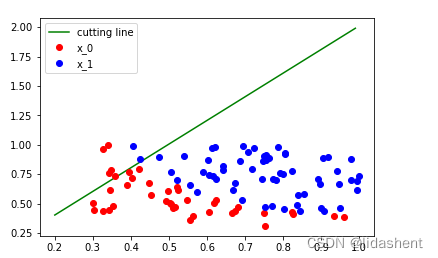
那么毫无疑问的,对于每一个坐标点[x,y]的分类是错误的,这里我们设置w的参数为2,生成两个w为xy加权重
但同时每次都手动更新一批wb是不合适的,应该做到w一次设置,自动更新,我们只关心w的数量和步长,手动调整w
变化不是我们应该关心的,我们需要一个w自动优化器

torch.optim接受一个nn.Parameter所定义的数据类型,然后自动对其中的所有数据进行更新维护
nn.Parameter默认带梯度,而Variable默认不带梯度
如果只是遍历更新参数似乎也并无必要,实际上optim带有众多参数优化器,比如SGD梯度下降方法来更新参数
这里设置学习率为1
以后更新参数只需要两行代码,不涉及具体参数操作

w=nn.Parameter(torch.randn(2,1))
b=nn.Parameter(torch.zeros(1))
optimizer=torch.optim.SGD([w,b],lr=1.)
for e in range(1000):
    # 前向传播
    y_pred = logistic_regression(x_data)
    loss = binary_loss(y_pred, y_data) # 计算 loss
    # 反向传播
    optimizer.zero_grad() # 使用优化器将梯度归 0
    loss.backward()
    optimizer.step() # 使用优化器来更新参数
    # 计算正确率
    mask = y_pred.ge(0.5).float()
    acc = (mask == y_data).sum().data[0] / y_data.shape[0]
    if (e + 1) % 200 == 0:
        print('epoch: {}, Loss: {:.5f}, Acc: {:.5f}'.format(e+1, loss.data[0], acc))

画出新分类图

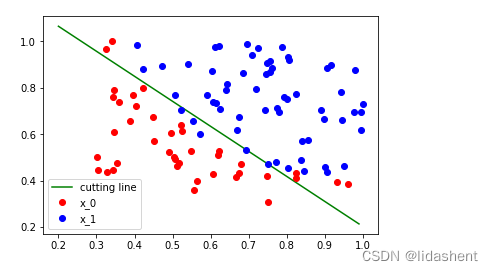
其实不仅仅w参数有优化器,对于loss函数也有优化器,这意味着对于常见的分类可以直接使用预设的优化器,而不用自己来实现,而且预设的优化器底层用c++实现,相比于我们自己写的效率更高
线性回归里,上一次使用的计算平方差的优化器函数为nn.MSE()
而逻辑回归里使用的二分类优化器函数为nn.BCEWithLogitsLoss(),这个损失函数优化器还集成了sigmoid,那么之前在计算真实值与推测值矩阵计算之后再进行的sigmoid得到概率操作就不用做了,直接调用这个函数输入预测值和真实值,得到的就是预测概率的损失值的和的平均值(原来的功能,都一样,更快而已)
得到loss优化器对象,计算损失值,在大型网络中预设的loss运行速度更为明显

# 使用自带的loss
criterion = nn.BCEWithLogitsLoss() # 将 sigmoid 和 loss 写在一层，有更快的速度、更好的稳定性
w = nn.Parameter(torch.randn(2, 1))
b = nn.Parameter(torch.zeros(1))
def logistic_reg(x):
    return torch.mm(x, w) + b
optimizer = torch.optim.SGD([w, b], 1.)
for e in range(1000):
    # 前向传播
    y_pred = logistic_reg(x_data)
    loss = criterion(y_pred, y_data)
    # 反向传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    # 计算正确率
    mask = y_pred.ge(0.5).float()
    acc = (mask == y_data).sum().data[0] / y_data.shape[0]
    if (e + 1) % 200 == 0:
        print('epoch: {}, Loss: {:.5f}, Acc: {:.5f}'.format(e+1, loss.item(), acc))

一些补充:

1. 当jupyter出现问题时重启一下也许就可以 代码过了保质期变得不可信任,文件不能加载,重新信任一下
   为什么要将numpy数据转化为torch数据
   因为torch数据被优化了,可以放在gpu上训练,支持自动求导,非常适合矩阵运算
   同时不要混淆list和numpy区别,list是python提供的可变列表,支持多种元素
   而numpy则长度不可变,只支持同类型元素,但同时速度更快,结构更加紧凑,提供了多种操作函数
   往往是先将list转化为numpy然后再转为torch
   这里设定了numpy每个元素为float32类型,代表所有numpy的所有行的前两个元素形成的列表被转化为torch格式

np_data=np.array(data,dtype='float32')
x_data=torch.form_numpy(np_data[:,0:2])

同时对于目标数据,需要将其排成一列

y_data=torch.from_numpy(np.data[:,-1]).unsqueeze(1)

clamp是一个判断语句,如果y_pred 或者1-y_pred小于这个数值就设置为这个数值
因为log的x区间不能小于等于0
逻辑回归函数调用sigmoid来对矩阵运算的结果进行分类,得到分类概率列表
loss求解损失函数中,会计算出预测值和真实值之间的log,并对输入的x矩阵所有数据的log差求和求平均值mean

ge(0.5)是一个比较器,低于此值归零,高于此值归1,用于分类,返回值与原数据类型相同
(mask==y_data).sum()统计两个torch对象有多少相等的,t这是orch对象的函数,作为神经网络的数据元素,它具备众多函数方法为了神经网络服务

多层神经网络

之前的线性回归模型和逻辑回归模型,因为都涉及到一层w的运算,都被视作单层神经网络
无非是不断优化一层w的值到合适位置而已

事实上,复杂而有效的神经网络是深层的,往往波浪式的w向前传递,同时模拟人脑神经元激活阈值的原理,提出了激活函数
sigmoid



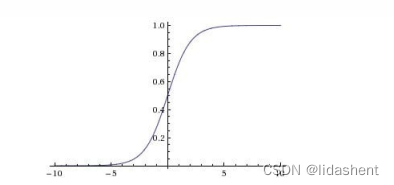
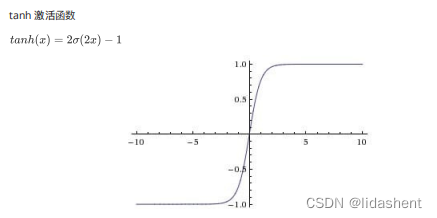
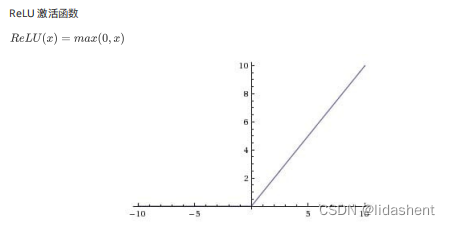
越来越多的实践表明relu的优化效果更好,一层网络是max(0,wx+b),二层就是w2max(0,w1x+b1)+b2
那么为什么需要激活函数呢?
本质上讲激活函数让神经网络有了深层的可能,通过改变w使得网络可以拟合成各种情况
如果不使用激活函数来改变网络形状,那么最后就会变成
w1x w2(w1x) w3(w2(w1x) ) w1w2w3…x Wnx 归根究底还是单层神经网络

多层网络搭建

解决多分类问题

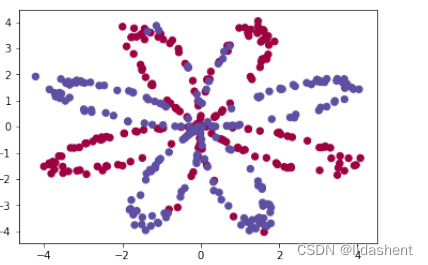
画出分类图形函数::

def plot_decision_boundary(model, x, y):
    # Set min and max values and give it some padding
    x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
    y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(x[:, 0], x[:, 1], c=y.reshape(-1), s=40, cmap=plt.cm.Spectral)

传入模型和数据,即可对数据进行可视化分类

xx,yy=np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))

meshgrid传入两个一维数组,生成两个二维数组,xx的shape为(y_max-y_min,x_max-x_min)
yy的shape为(x_max-x_min,y_max-y_min),这个很好理解,可以看做画了一个坐标网格,xx和yy为每一个点都设定了坐标

z=model(np.c_[xx.ravel(),yy.ravel()])

将xx和yy一维展开,然后由np.c_得到它们所标记的每一个点,每个点交给模型,让模型算出新的目标numpy数组,然后让其形状大小和xx相同,这样方便展开绘画

plt.contourf(xx,yy,z,cmap=plt.cm.Spectral)

xx和yy绘制网格,z来画出分割点,cmap来设定颜色,设定为渐变色,从高到低由红绿蓝渐变方便查看

plt.scatter(x[:,0],x[:,1],c=y.reshape(-1),s=40,cmap=plt.cm.Spectral)

根据坐标绘制散点图,参数为x,y坐标,c函数值,散点大小,颜色渐变

那么要分类的图形是怎样的?可以画出一个图

我们要画的是一个复杂的花色图像,红蓝相间,由sin和cos函数组合而成
构思逻辑如下:
指定某个范围的数据生成sin和cos的x坐标值列表
然后根据这些坐标值生成新的坐标y值,即sin,cos值
通过公式[sin(x)*sin(x),sin(x)*cos(x)]来说生成每一组xy的坐标点来进行绘图
然后绘制这些坐标即可

allPoint=400
halfCategory=int(allPoint/2)
xy=np.zeros((allPoint,2))#存储x和y值的坐标矩阵,数据矩阵,400行,2列
y=np.zeros((allPoint,1))#存储y值的坐标矩阵,分类目标矩阵,400行
for i in range(2):#可视化视图
    ix=range(i*halfCategory,(i+1)*halfCategory)#对xy坐标进行圈定范围
    t=np.linspace(i*3.12,(i+1)*3.12,halfCategory)#生成sin,cos演化周期的x值
    x=30*np.sin(8*t)#生成sinx值,用于生成花型图案的基础y矩阵
    xy[ix]=np.c_[x*np.sin(t),x*np.cos(t)]#构建一个二维矩阵,有两个特殊的一维矩阵构成,将这两个一维矩阵组合生成xy坐标矩阵,放入xy中
    y[ix]=i#构建坐标值矩阵
plt.scatter(xy[:,0],xy[:,1],c=y.reshape(-1),s=40,cmap=plt.cm.Spectral)

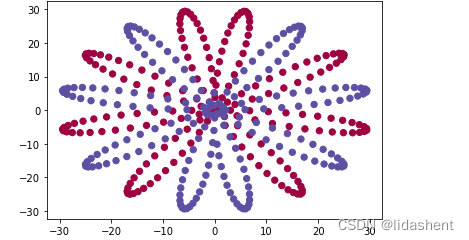
那么红蓝分类的点就当作原始数据,y值目标值当做分类数据,这样xy和y数据矩阵就构建好了
那么接下来我们使用逻辑回归一层分类，二层网络，三层网络分别进行实验分类效果
构建训练参数x,y
初始化wb,设置参数优化器和loss优化器
循环100次优化wb，再次绘图

x_trainData=torch.from_numpy(np.array(xy)).float()
y_trainData=torch.from_numpy(np.array(y)).float()
w=nn.Parameter(torch.randn(2,1))
b=nn.Parameter(torch.randn(1))
def logistic_regression(x):
    return torch.mm(x,w)+b
optimizer=torch.optim.SGD([w,b],1e-1)
lossor=nn.BCEWithLogitsLoss()
for i in range(100):
    y_pred=logistic_regression(x_trainData)
    loss=lossor(y_pred,y_trainData)
    optimizer.zero_grad()
    optimizer.step()

将参数进行新绘图

def plot_logistic(x):
    x = Variable(torch.from_numpy(x).float())
    out = F.sigmoid(logistic_regression(x))
    out =out.ge(0.5).float()
    return out.data.numpy()
plot_decision_boundary(lambda x_trainData: plot_logistic(x_trainData), x_trainData.data.numpy(), y_trainData.data.numpy())
plt.title('logistic regression')

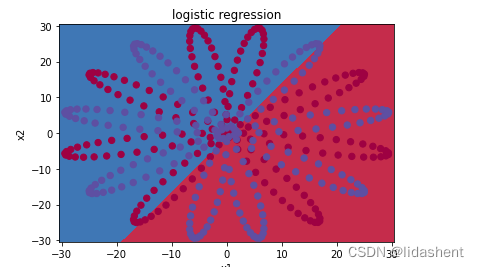
效果并不理想，只能进行简单的二分类
我们构建一个两层图像，并使用tanh作为激活函数，再次看效果
第一层网4个神经元，经过它之后原有的数据被扩容了4倍，如果熟悉矩阵运算，假设原数据为x[100,2],经过w[2,4],就会变成[100,4],然后经过激活函数剪枝，激活部分有用的神经元，最后由一个神经元输出01分类数据
矩阵乘法就是，由mxn的矩阵与nxz的矩阵相乘，得到mxz的新矩阵，其中新矩阵的每一个数值都是由行列坐标ij计算，行对应m的行，列对应z的列，对应值相乘的和为新矩阵的值
比如

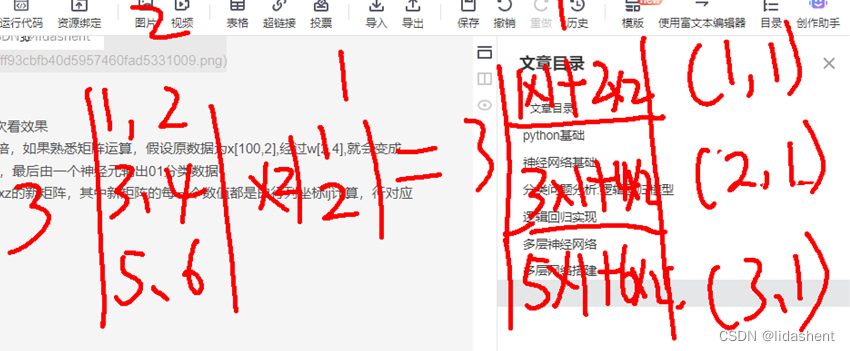
w1=nn.Parameter(torch.randn(2,4))
b1=nn.Parameter(torch.randn(4))
w2=nn.Parameter(torch.randn(4,1))
b2=nn.Parameter(torch.randn(1))
# 定义模型
def two_network(x):
    x1 = torch.mm(x, w1) + b1
    x1 = F.tanh(x1) # 使用 PyTorch 自带的 tanh 激活函数
    x2 = torch.mm(x1, w2) + b2
    return x2
optimizer=torch.optim.SGD([w1,b1,w2,b2],1.)
for i in range(1000):
    y_pred=two_network(x_trainData)
    loss=lossor(y_pred,y_trainData)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if i%200==0:
        print(loss.item())

分类效果并不好，但相比于逻辑回归有了改善

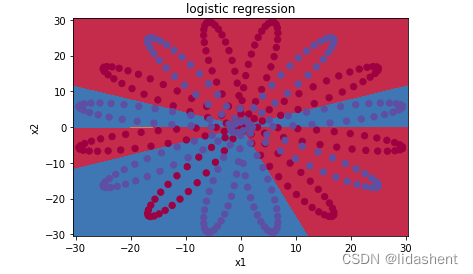
如果想要取得更好的效果，我们可以增加训练神经元的次数和深度，然而需要注意的是神经元的次数优势并不会带来更好的训练效果，因为参数优化有极限的，但是深度结构的改变会带来质的飞跃
我们可以尝试增加多个神经元来模拟分类效果，但是在一些大型项目中这样的神经元可能有几百亿个，逐个设置参数是不合理的,因此提供了参数初始化工具,在设置网络层数的同时将网络结构一并设计,这样我们只需要关注网络的参数和层数如何设计而不用做重复劳动
一个是Sequential，一个是 Module
会得到一个神经网络模型,同时设置了每层神经元的数量和网络结构

seq_net=nn.Sequential(
nn.Linear(2, 10),
nn.Tanh(),
nn.Linear(10, 8),
nn.Tanh(),
nn.Linear(8, 5),
nn.Tanh(),
nn.Linear(5, 1)
)

和单层设计一样,我们可以随意的查看每层的结构和权重参数

seq_net[0]
#Linear(in_features=2, out_features=10, bias=True)

w1=seq_net[0].weight

接下来只需要设置参数优化器,loss优化器,将数据导入seq_net就能够执行训练了,lossor之前已经进行过定义,就是nn.BCEWithlogitsloss()

param=seq_net.parameters()
paramOptimizer=torch.optim.SGD(param,1.)
for i in range(20000):
    y_pred=seq_net(x_trainData)
    loss=lossor(y_pred,y_trainData)
    paramOptimizer.zero_grad()
    loss.backward()
    paramOptimizer.step()

查看多层网络的分类效果

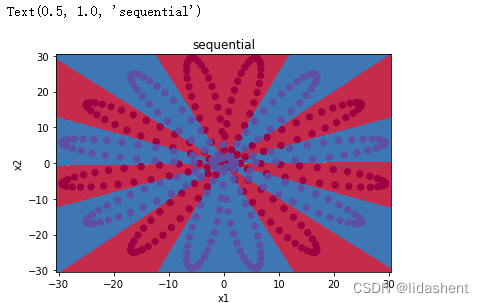
当然对于网络结构还有更好的写法,使用modul定义模型更符合语法规范
模板为:
可以设计网络结构,然后设置前向传播如何构建,就像一个类调用
Module 里面也可以使用 Sequential

class 网络名字(nn.Module):
    def __init__(self, 一些定义的参数):
        super(网络名字, self).__init__()
        self.layer1 = nn.Linear(num_input, num_hidden)
        self.layer2 = nn.Sequential(...)
        ...

        定义需要用的网络层

    def forward(self, x): # 定义前向传播
        x1 = self.layer1(x)
        x2 = self.layer2(x)
        x = x1 + x2
        ...
        return x

如下设计一个三层网络,查看权重和网络层结构就像类调用一样

class modelNet(nn.Module):
    def __init__(self,inputLayer,hiddenLayer,outputLayer):
        super(modelNet,self).__init__()
        self.layer1=nn.Linear(inputLayer,hiddenLayer)
        self.layer2=nn.Tanh()
        self.layer3=nn.Linear(hiddenLayer,outputLayer)
    def forward(self,x):
        x=self.layer1(x)
        x=self.layer2(x)
        x=self.layer3(x)
        return x
mNet=modelNet(2,4,1)
mNet.layer1.weight

对其进行训练

mParamOptimizer=torch.optim.SGD(mNet.parameters(),1.)
for i in range(20000):
    y_pred=mNet(x_trainData)
    loss=lossor(y_pred,y)
    mParamOptimizer.zero_grad()
    loss.backward()
    mParamOptimizer.step()

保存模型

1,将网络结构和参数一起保存
前面是网络模型,后面是路径

torch.save(seq_net, 'save_seq_net.pth')

读取模型和参数,得到新的神经网络对象

seq_net1 = torch.load('save_seq_net.pth')

2,只保存参数

# 保存模型参数
torch.save(seq_net.state_dict(), 'save_seq_net_params.pth')

已经有网络结构了,只需要加载预设参数
得到新的神经网络

seq_net2.load_state_dict(torch.load('save_seq_net_params.pth'))