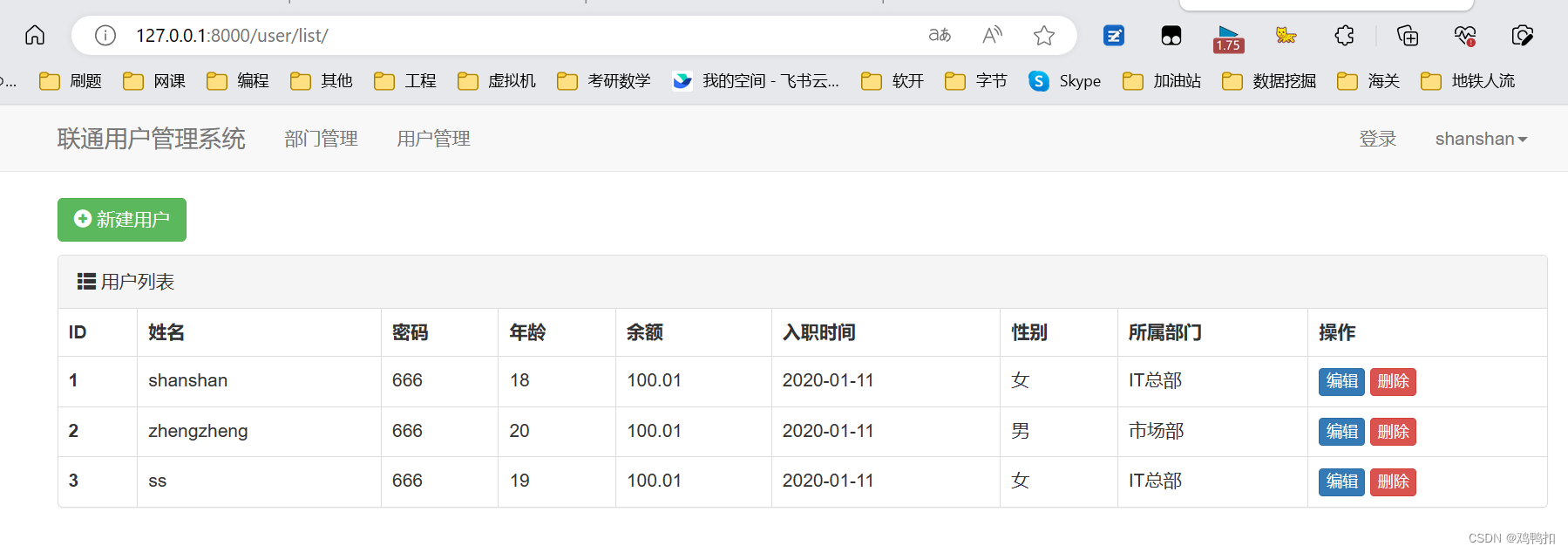
题目描述：

---

分析：

乍一看我还以为是贪心！
猫 想想感觉没问题
但是局部最优并不能保证全局最优
比如这组数据

19 19 19 19
20 20
20 20

如果按照贪心的做法，答案是20*20*2
但是其实答案是19*20*4

因此这道题用贪心是不对的

于是我们考虑dp
可以观察到这道题的n非常小只有200
这就暗示我们这道题可以用$n^3$的做法去解决

那么我们就可以这样设dp状态
$f[i][j][k]表示用三个颜色分别用了前i,j,k个数，所能获得的最大价值$
如何转移呢？
考虑一次可以取两个数
也就是说可以取12,23,13
那么分别从这三种状态转移过来即可

有的时候记忆化搜索比dp更好写！

---

Code

#include<bits/stdc++.h>
using namespace std;

const int N = 210;
int r,g,bb;
int a[N],b[N],c[N];
int f[N][N][N];

bool cmp(int x,int y){
	return x>y;
}

int Dfs(int x,int y,int z){
	if (f[x][y][z]) return f[x][y][z];
	int Max = 0;
	if (x && y) Max = max(Max,Dfs(x-1,y-1,z)+a[x]*b[y]);
	if (x && z) Max = max(Max,Dfs(x-1,y,z-1)+a[x]*c[z]);
	if (z && y) Max = max(Max,Dfs(x,y-1,z-1)+b[y]*c[z]);
	return f[x][y][z] = Max;
}

int main(){
	cin>>r>>g>>bb;
	for (int i = 1; i <= r; i++) cin>>a[i];
	for (int i = 1; i <= g; i++) cin>>b[i];
	for  (int i = 1; i <= bb; i++) cin>>c[i];
	sort(a+1,a+r+1);
	sort(b+1,b+g+1);
	sort(c+1,c+bb+1);
	cout<<Dfs(r,g,bb)<<endl;
	return 0;
}