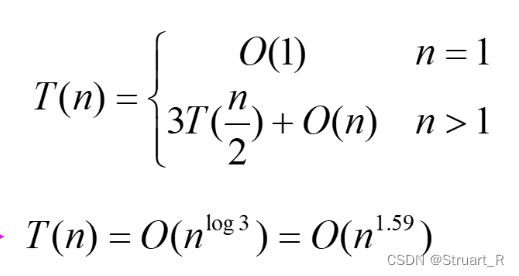文章目录
- 前言
- 绪论
- 数据结构基本概念
- 基本概念
- 数据结构三要素与ADT
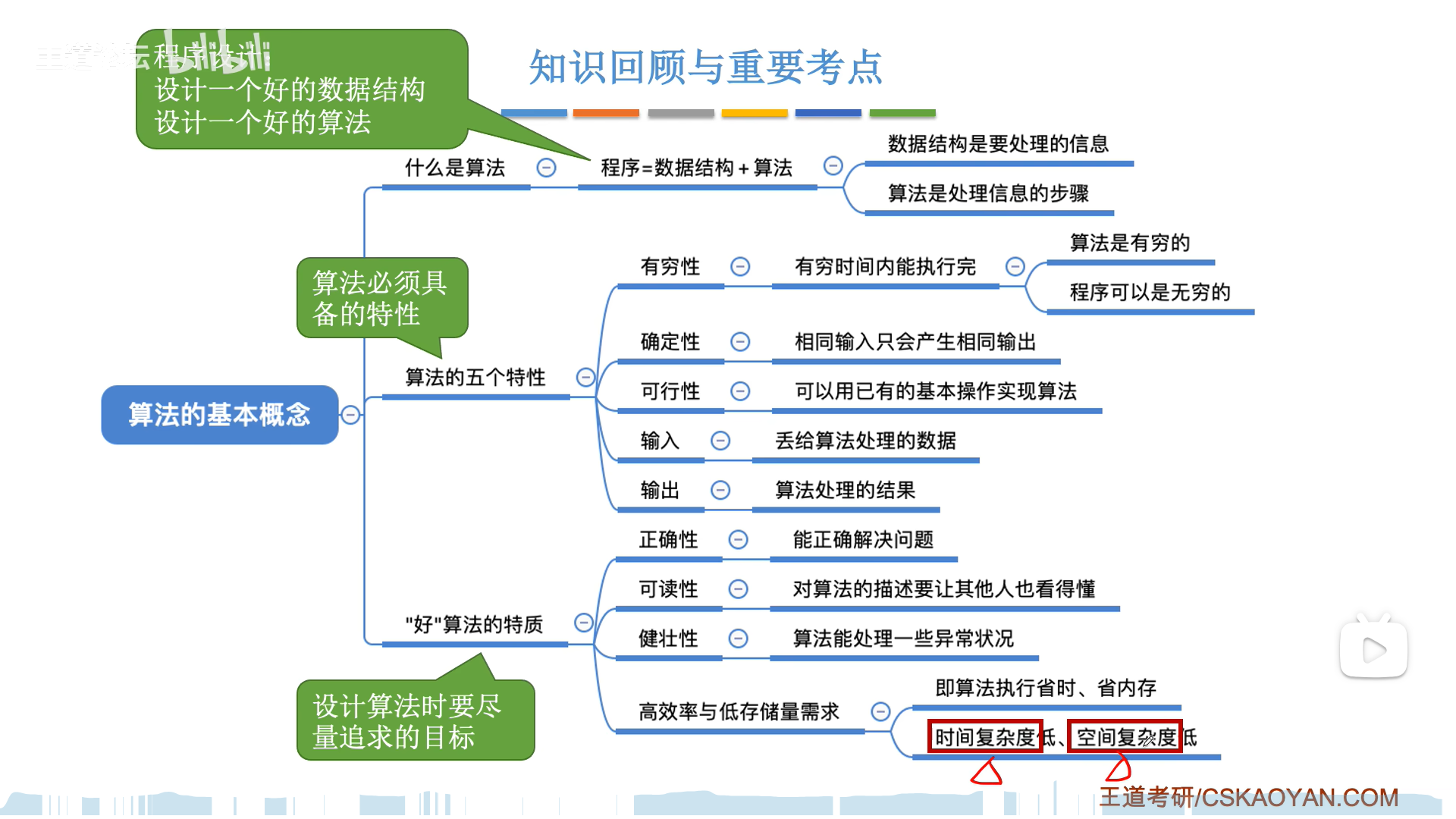
- 算法基本概念
- 算法定义
- 算法五个基本特性
- 好算法的进阶特性
- 算法复杂度
- 时间复杂度
- 空间复杂度
- 线性表
前言
数据结构的笔记相比于其他3门,笔记的重要性要低很多,毕竟对于选择408的同学来说,大二时候应该有足够的时间学习,所以基础是比较好的,再加上csdn上一大堆数据结构和算法的帖子,我再重复造轮子也没啥意思了。
所以我这篇文章不打算写的很细节,就是单纯地把思路提纯出来,并附上自己的理解,再搭配思维导图就行了,而不去记录过于细节的知识。
绪论

408的4门课,构建了计算机的根基。
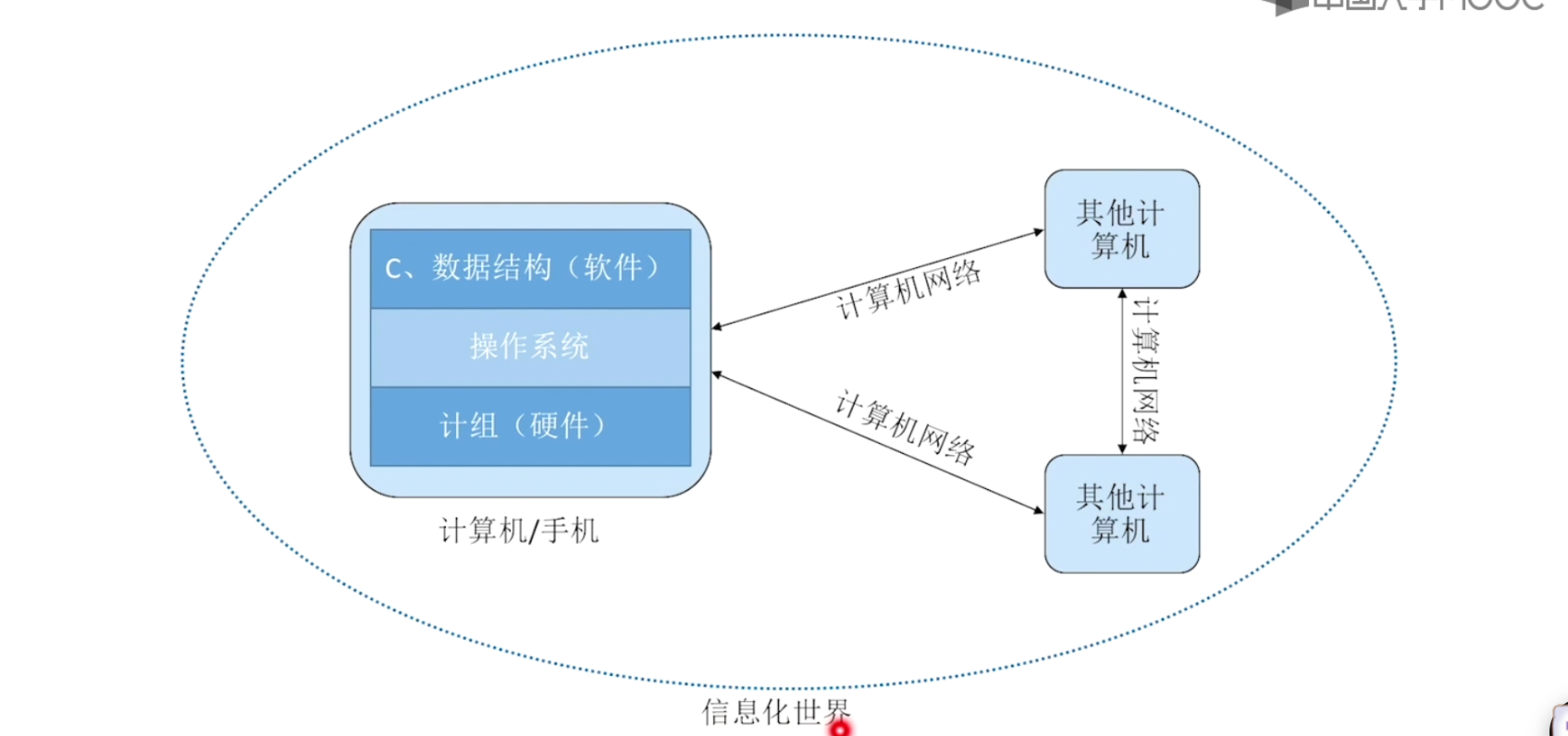
计算机处理信息的原理如下:
- 现实-计算机。从现实到计算机,需要经过硬件+软件的转化,其中就需要数据结构表示现实事物。
- 内部处理。内部处理的过程中,需要高效,因此诞生了各种算法。
- 计算机-显示到现实。是步骤1的逆过程。
数据结构基本概念
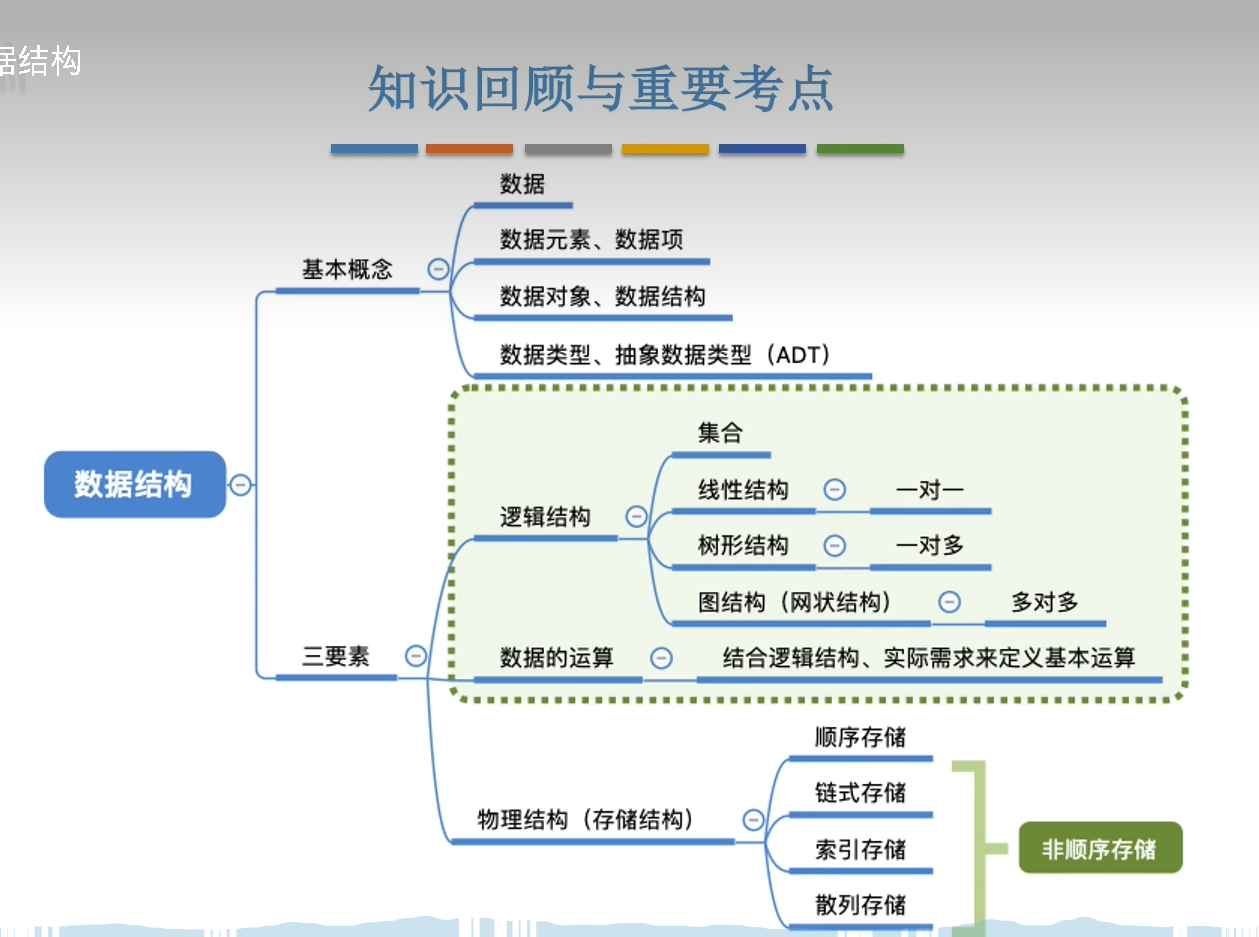
基本概念
现实世界有信息,通过数据来承载信息,而数据可以被计算机所处理。
数据的形式可以是数值和非数值,但是底层只能是0和1,这是计算机的数学原理和基础构造决定的。
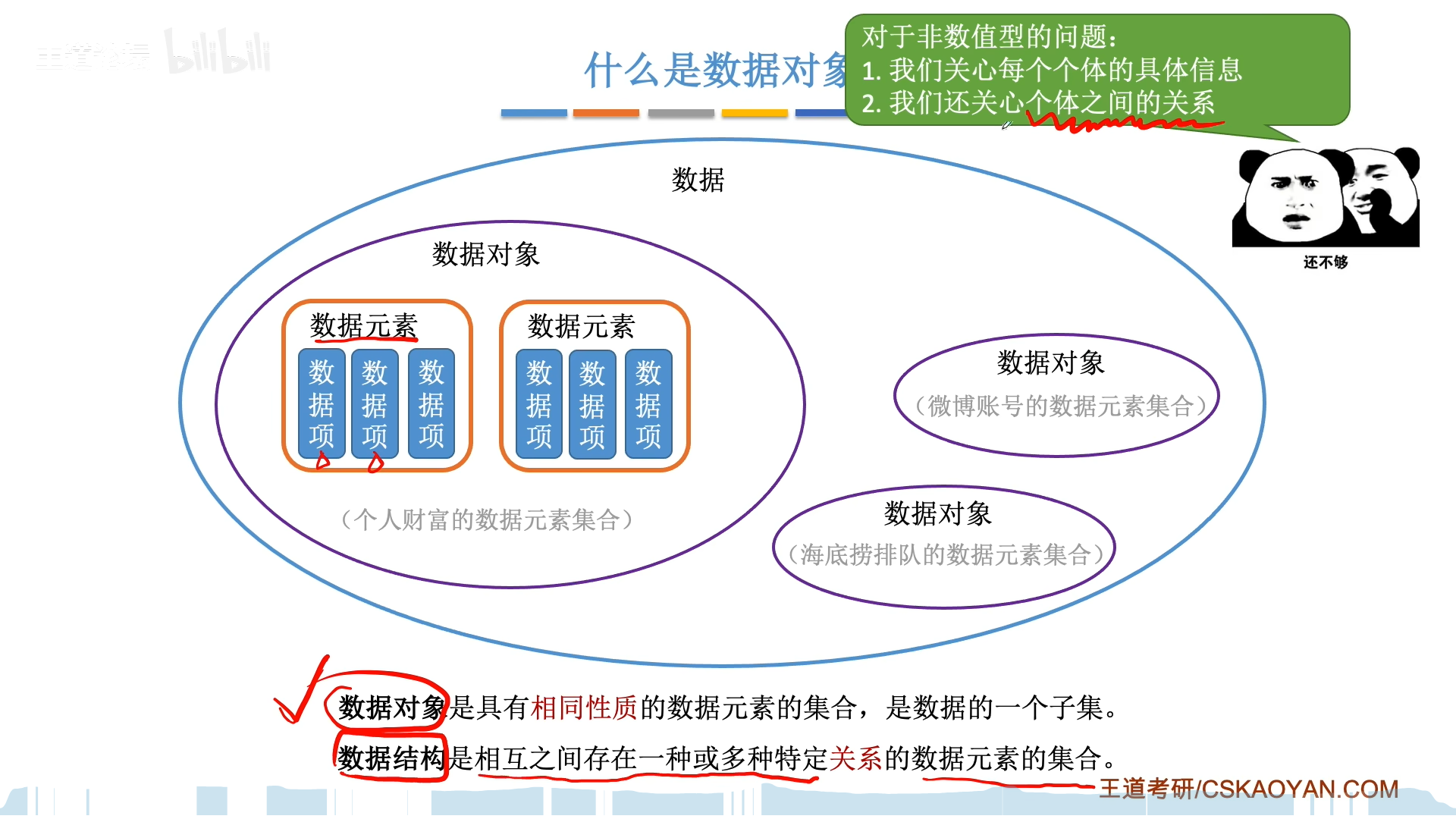
- 数据项
- 在C语言中,int,float这些东西,都是最基本的数据单位,就是所谓的数据项
- 数据项这个概念很矛盾,一边说不可分,但是另一边,有一些特殊的组合项是仍然可分的,比如如果用一个结构体当数据项,那么这个数据项就是组合项。
- 我们姑且忽略组合项这种东西,就强行把数据项定义为不可分的基本单位就好。
- 数据元素
- 在C语言中就是一个结构体实例,代表着一个具体的个体,比如张三。
- 数据对象
- 同一类(相同性质)数据元素的集合
- 在C语言中,就是同一个结构体原型实例化后的所有结构体实例的集合
- 数据
- 数据对象的集合,代表了计算机中所有的数据

概念讲完了,然后就是数据结构的定义了。
数据结构描述了一个数据对象内部,不同的数据元素组合的方式。
数据结构是普遍适用的,因为不关心数据元素内部的数据项,所以凡是数据元素,都可以用数据结构去组织,因此不同的数据对象内部,完全可以适用同一个数据结构去组织。
数据结构三要素与ADT
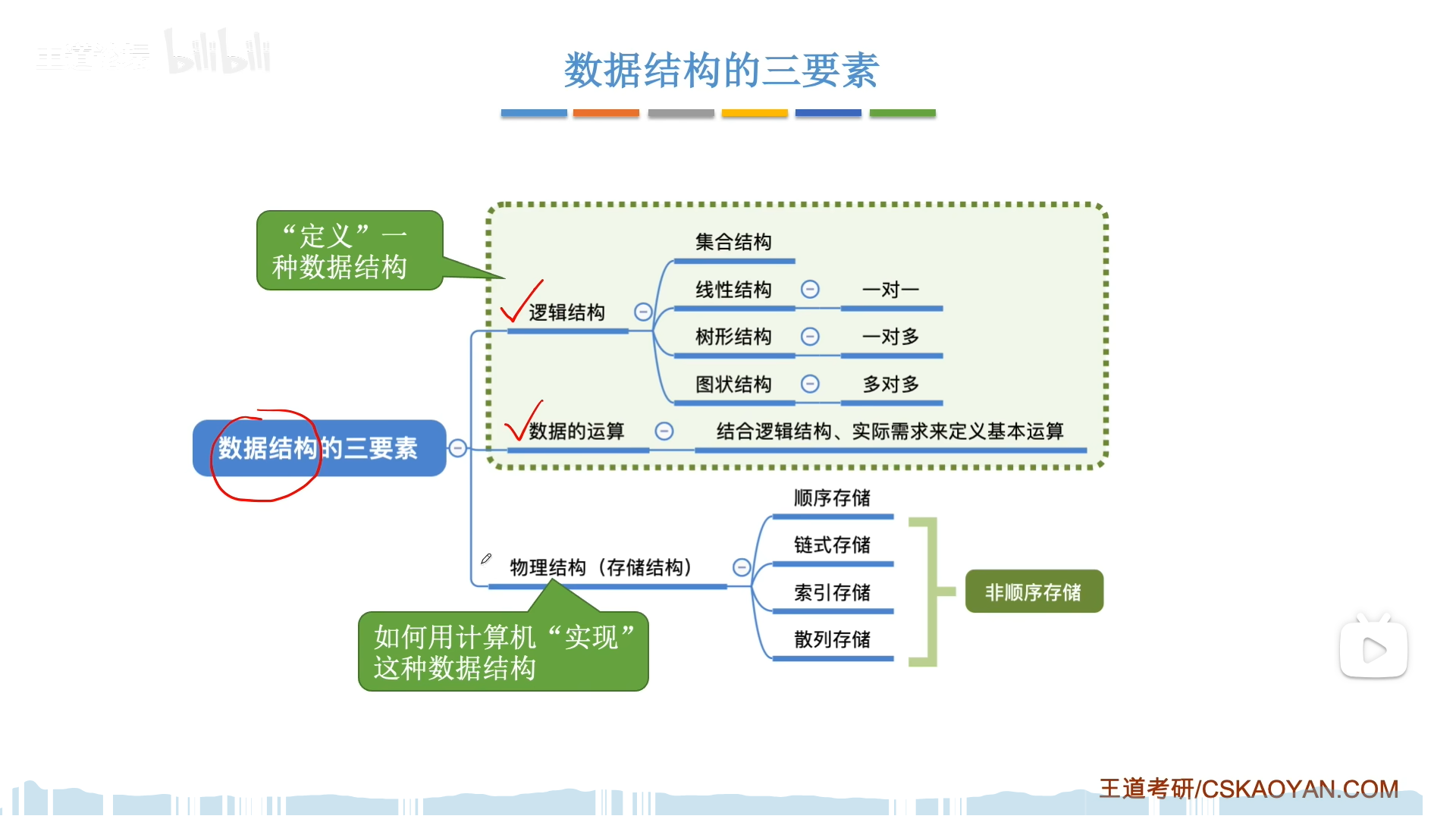
数据结构:
- 定义:使用者视角
- 逻辑结构定义。是什么
- 数据运算定义。可以干什么
- 实现:开发者视角,需要考虑储存结构,这会影响到空间效率和时间效率。
- 顺序,链式。
- 索引储存。索引表通过key-value方式记录数据地址,给定一个key,可以马上得到地址,进而马上得到储存在内存中的值。优点是速度快,缺点是浪费一个索引表的空间,浪费内存。

- 散列储存。散列储存和索引一样快,但是却不需要借助索引表。散列储存本质上是通过一个映射函数代替索引表,这个函数就是Hash函数,输入一个key,直接输出地址,和索引表效果相同,但是并不占用内存。优点同索引,缺点在于,散列函数并不能100%利用内存空间,和索引储存半斤八两,都会浪费内存。
我们再把视角抬高,你会发现数据结构其实是一种ADT(抽象数据类型)。
数据类型=值的范围+可进行的操作,进而可以细分为原子类型(int,float)和结构类型(struct)
数据结构定义=逻辑结构+可进行的操作,和数据类型本质是一样的,所以把数据结构成为抽象数据类型,说白了,ADT描述了数据结构的逻辑部分,隐藏了实现部分,可以拿来即用。
定义好数据类型或者ADT后,使用者就可以使用,无论是哪种,使用者都可以拿来即用。

算法基本概念
算法定义
数据结构是原料,算法是处理步骤。
具体来说,数据结构负责将现实问题装入计算机,而算法就是一系列求解问题的步骤,将计算机中的问题求解出来。
算法五个基本特性
算法其实就是一个可以执行下去(有穷,可行)的函数(输入,确定,输出)
- 有穷性。
- 步骤有穷,时间有穷
- 程序≠算法,程序可能无穷(死循环)
- 确定性。
- 说白了算法就是一个函数,x确定y就确定
- 描述不能有歧义,比如最小,如果有两个一样小的,那就要修改成
第一个最小的
- 可行性。
- 算法=基本运算有限次组合。其实和有穷性差不多
- 输入。
- 可以为0个
- 输出
- 至少一个,不然没啥用
算法只要求这些,不强求正确,只要是确定的就行。
好算法的进阶特性
- 正确。
- 实用算法的基本要求,算法不一定要求对,但是拿来用一定得对
- 可读。
- 伪代码或者代码+注释
- 健壮性。
- 容错率
- 高效率和低储存量需求
- 时间复杂度低和空间复杂度低
算法复杂度
算法复杂度=时间复杂度+空间复杂度
事后统计(×):评估算法不应该用实际执行时间,因为影响因素太多了,而且有些算法不能事后统计
事前估计(√)
时间复杂度
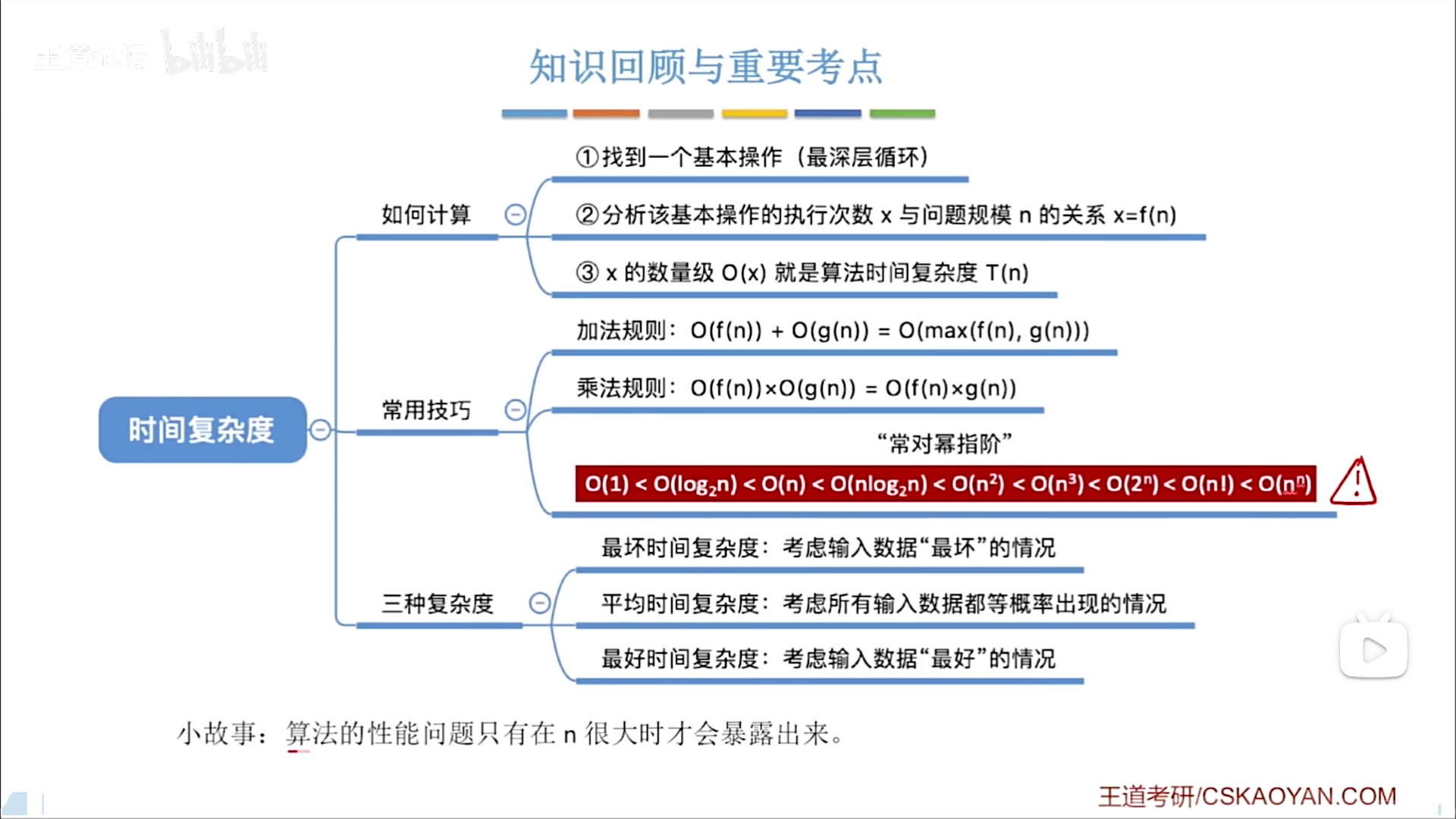
T:时间复杂度
n:问题规模
使用渐进记法,只考虑最高阶部分,且系数忽略,
T
(
n
)
=
O
(
n
3
)
T(n)=O(n^3)
T(n)=O(n3)
这个记法代表当n趋于无穷时,T和n是同阶无穷大量,比值为k,这个k是被我们忽略为1的
具体的高阶比较,下图给出直观理解,n的n次方>阶>指>幂>对>常

具体分析的时候,关键在于要写出基本操作执行次数x的表达式,用n表达x,或者是写出n和x的关系后化简,然后运用复杂度运算规则得到最后的渐进复杂度:
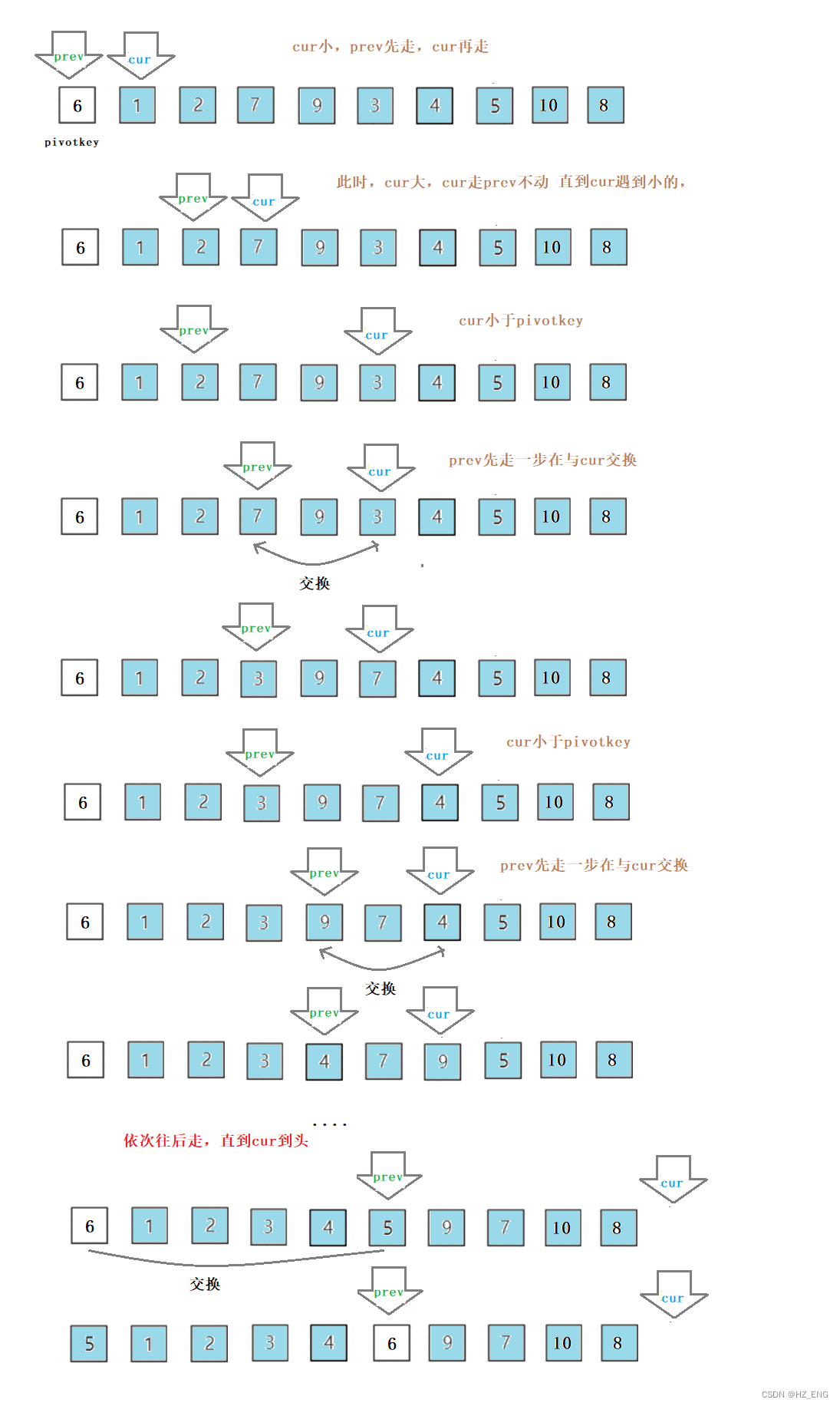
下面这个例子,这个大循环就是要分析的目标,内层循环总共执行n方次,而外层循环是n次,虽然可以一眼看出来是n方,但是还是要写出来表达式后再化简。
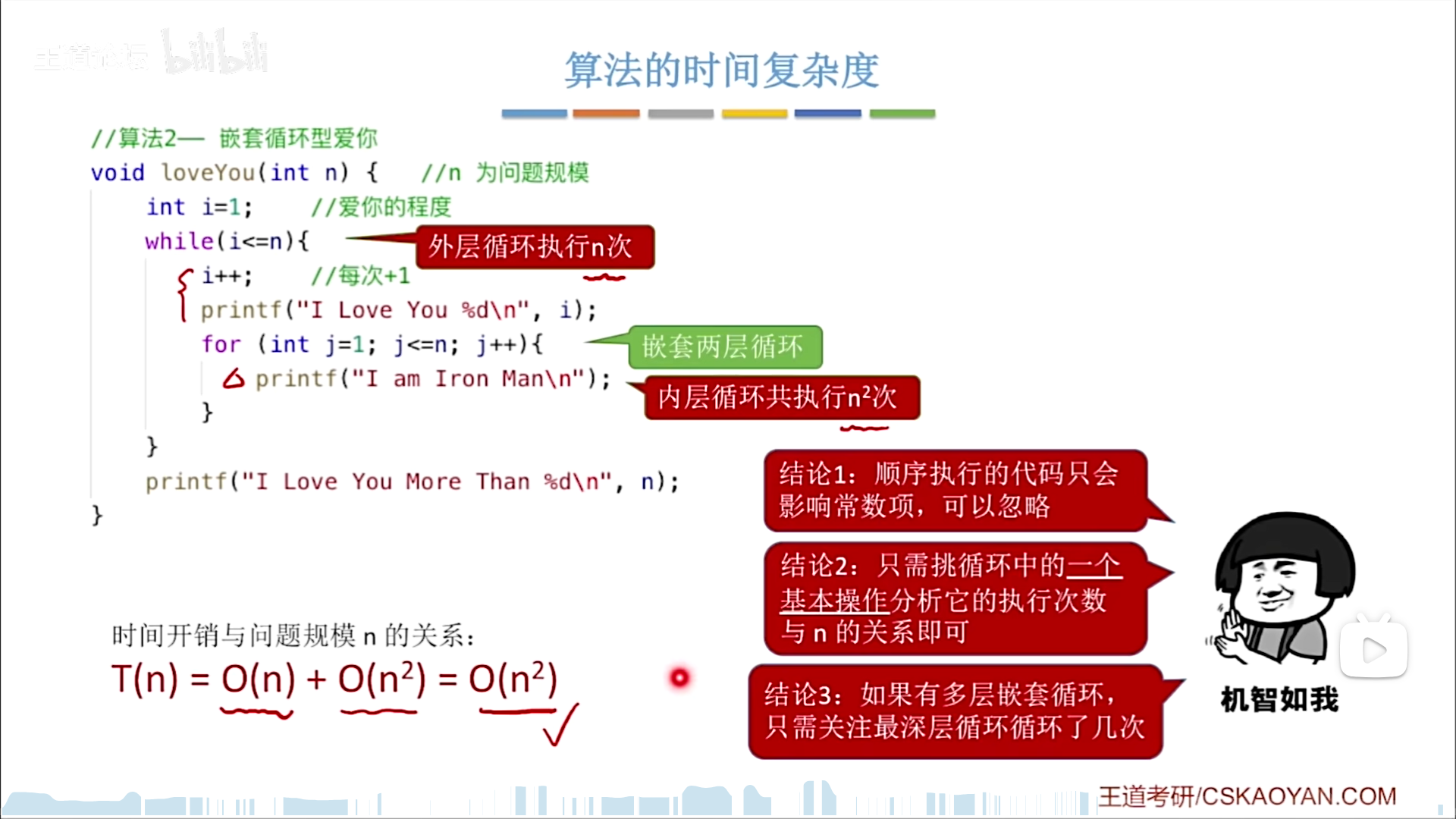
面对复杂问题,应该写出x,变形,化简,得到目标的阶数。

有的时候,x与具体情况有关,那么就有三种计算方法:
- 最好。参考意义不大
- 最坏。常用
- 平均。常用,这个平均需要写出概率分布,计算期望

空间复杂度

S:空间复杂度
S是空间开销与n的关系
内存开销来源:
- 变量定义/malloc
- 函数调用
递归调用的空间复杂度就有点像循环时候的时间复杂度,有时候也会算一个式子。