# 引言
深度残差网络的提出是深度学习领域的里程碑事件,它使得网络可以做大做深,现在主流的网络中都有残差结构
# 问题
- ##深度网络的退化
深度网络有一个普遍的问题:随着网络层数的增加,准确率是先增后减的,准确率增加是很好理解的,毕竟网络变深之后,模型的学习能力也随之变强,结果也相应地变好,但是结果变差是反直觉的,这种现象被称为网络退化,有人给出解释:模型的参数规模超过数据规模,模型可能发生了过拟合现象。但是作者通过实验指出,这种退化现象不是过拟合,事实上,训练集上的结果也变差了,过拟合并不会出现这种情况。
为了说明这一点,作者在CIFAR-10上分别使用20层的网络和56层的网络进行训练,并记录了训练误差和测试误差:

可以看到,在训练集上就出现了深的网络比浅网络效果更差的现象。下面从原理上进行分析
- ##梯度消失现象
梯度消失是深度神经网络训练中的一个常见问题。它指的是在网络的后向传播过程中,随着网络层数的增加,较浅的层在梯度更新时所受到的影响几乎为零,导致这些层的权重几乎不发生变化,模型的学习能力下降。梯度消失问题的主要原因之一是使用特定的激活函数,例如 $sigmoid$ 或 $tanh$ 函数。这些激活函数的导数在输入接近饱和区域时变得非常小,接近于零。当网络的深度增加时,这些较小的导数将被连续相乘,导致梯度指数级地减小,最终消失。以一个三层的神经网络、每层只有一个神经元为例,则有:
$$
x_{i+1}=\sigma(w_ix_i+b_i)\quad i=1,2,3 \\
\frac{\partial{y}}{\partial{x_1}}=\frac{\partial{y}}{\partial{x_3}}\cdot\frac{\partial{x_3}}{\partial{x_2}}\cdot\frac{\partial{x_2}}{\partial{x_1}}
$$
其中$x_1,x_2,x_3$分别为第1、2、3层网络的输入,$y=x_4$为网络的输出,由于每一层都经过激活函数,求导的结果会较小,因此最后相乘的结果也会很小,即浅层的网络的梯度很小,网络学习能力下降。
# 方法
作者提出了一个解决思路,我们希望经过一层后网络的输出结果$F(x)$不会比网络的输入$x$差,要实现这一点,我们希望网络能够在结果变差时直接拟合为网络的输入,作者认为学习一个恒等映射是困难的,而学习一个零映射是简单的,因此只需要在网络输出结果$F(x)$上加上一个这层网络的输入$x$,这样如果网络输出结果变差了,残差$F(x)-x$会被拟合为0,如下图所示:

从原理上来说,残差连接将公式做出了如下的改变:
$$
x_3=x_1+\sigma(w_2x_2+b_2)
\frac{\partial{y}}{\partial{x_1}}=\frac{\partial{y}}{\partial{x_3}}\cdot\frac{\partial{x_3}}{\partial{x_1}}=\frac{\partial{y}}{\partial{x_3}}(1+\frac{\partial{x_3}}{\partial{x_2}}\cdot\frac{\partial{x_2}}{\partial{x_1}})
$$
可以看到,由于多了1这一项,可以解决梯度消失这一问题。
- ## 模型结构
使用残差连接的模型结构如下:

# 实验
- ## ImageNet
作者在ImageNet上进行了实验,左图为不加残差结构的网络,右图为添加残差结构的网络。

可以发现,不使用残差结构,深层网络(34-layer)比浅层网络(18-layer)的训练误差更大,而加了残差结果的网络则不存在这个问题。
作者还进行了消融实验,对比了使用残差结构不同深度的下的网络的结果:

- ## CIFAR-10
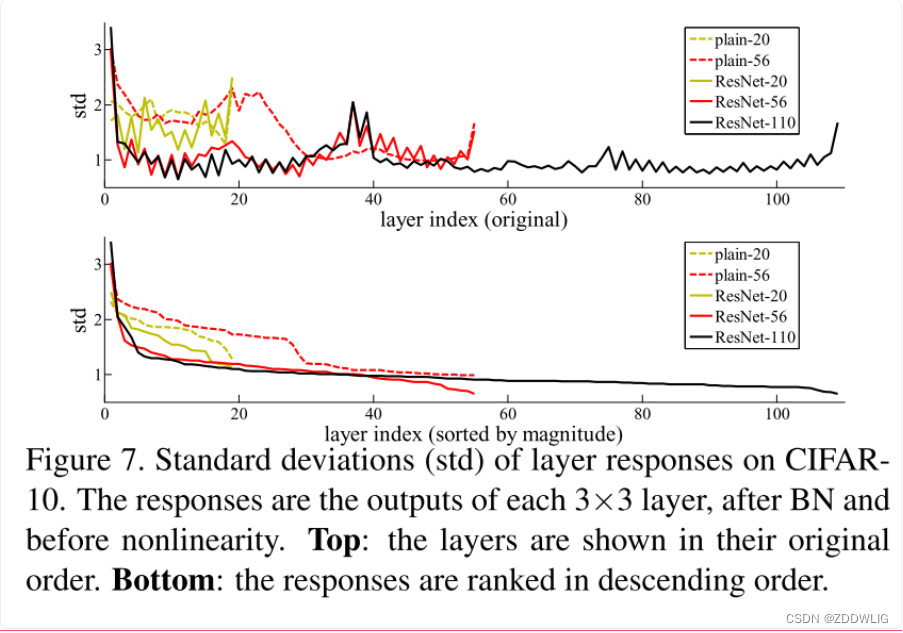
作者在CIFAR-10上测试了不同层数的网络的测试误差 下图是不同层数网络的在训练误差曲线的对比和标准差对比:
下图是不同层数网络的在训练误差曲线的对比和标准差对比:









![[sping] spring core - 依赖注入](https://img-blog.csdnimg.cn/a3c76dc697604e5bb00837dc50493e10.png)