---

一、问题描述

跳台阶_牛客题霸_牛客网 (nowcoder.com)

LCR 127. 跳跃训练 - 力扣（LeetCode）

---

二、解题思路 

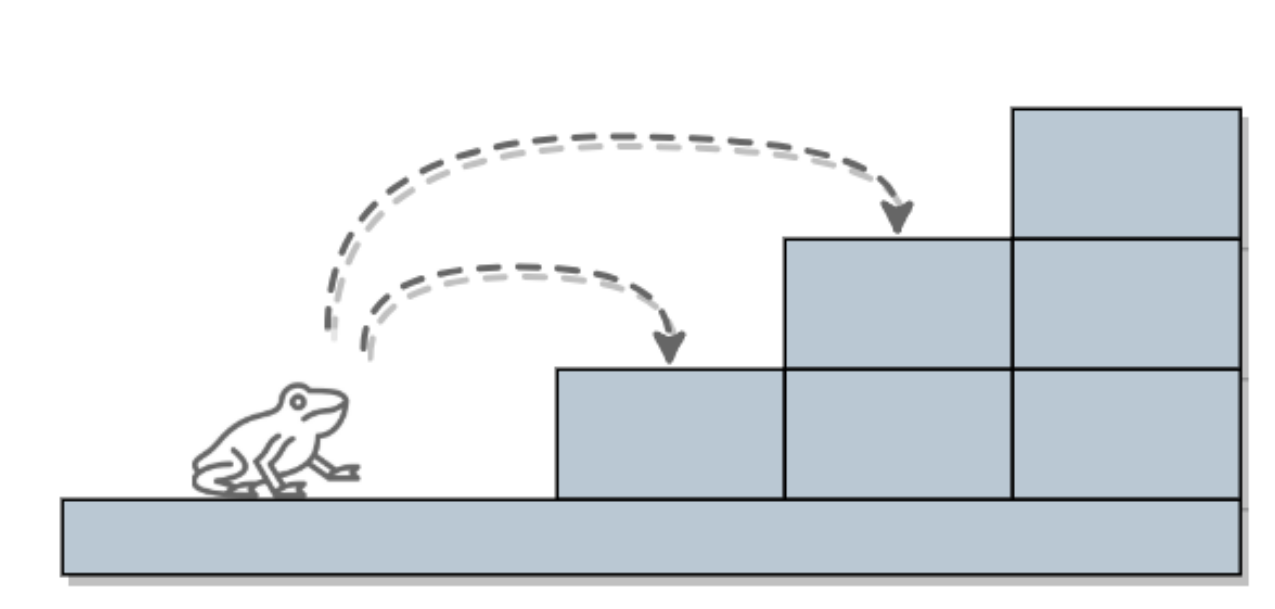
1、当 n = 1 时，一共只有一级台阶，那么显然青蛙这时就只有一种跳法

---

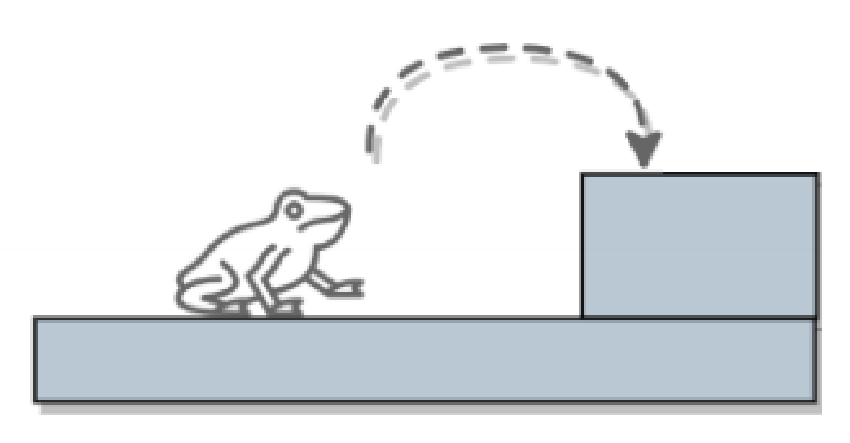
2、当 n = 2 时，一共有两级台阶，这时青蛙的跳法有两种

---

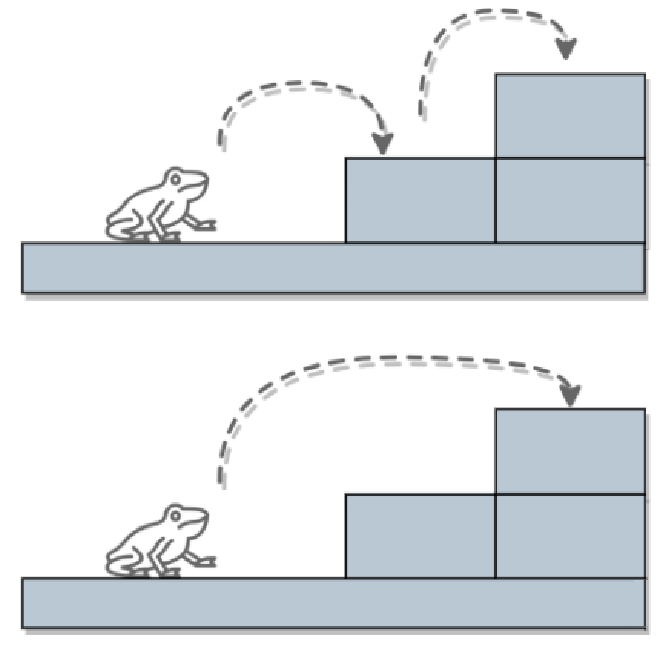
以此类推，通过这种思路来求解。该题要求的是青蛙从 0 ~ n 级台阶的所有跳法，我们可以假设跳上 n 级台阶一共有 f(n) 种跳法。从上面的图片我们可以知道青蛙的最后一步的跳法只有两种情况： 跳上 1 级或 2 级台阶。那就意味着如果青蛙选择跳 1 级台阶的跳法将与选择跳 2 级台阶时不相同：

• 当跳上 1 级台阶时： 还剩 n-1 个台阶，此情况共有 f(n-1) 种跳法；
• 当跳上 2 级台阶时： 还剩 n-2 个台阶，此情况共有 f(n-2) 种跳法。

可以得到 f(n) = f(n-1) + f(n-2) 。由此就可以不断递归下去，这与斐波那契数列的解题思路有异曲同工之处，唯一的不同在于起始数字不同。

• 青蛙跳台阶问题：f(0) = 1，f(1) = 1，f(2) = 2；
• 斐波那契数列问题：f(0)=0，f(1) = 1，f(2) = 1。

---

三、代码

#include <stdio.h>

// 求n台阶青蛙的跳法
int frog_jump_step(int n)
{
	// 对特殊情况作处理
	if (n == 1)
	{
		return 1;
	}
	if (n == 2)
	{
		return 2;
	}
	// 递归调用
	return frog_jump_step(n - 1) + frog_jump_step(n - 2);
}
int main()
{
	int n = 0;
	scanf("%d", &n);

	int ways = frog_jump_step(n);
	printf("%d\n", ways);

	return 0;
}

---

四、扩展

跳台阶扩展问题_牛客题霸_牛客网 (nowcoder.com)

---

1、解题思路

（1）思路一

这里的青蛙比上面的青蛙更厉害一些，它一次可以跳 1 阶，2阶，3阶... ....。所以如果想要跳到第 n 个台阶，我们可以从第 1 个台阶跳上来，也可以从第 2 个台阶跳上来... ...，所以递推公式是：f(n) = f(n-1) + f(n-2) + ... ... + f(2) + f(1);

同样在跳到第 n-1 个台阶时，也可以列出下面这个公式：

f(n-1) = f(n-2) + ... ... + f(2) + f(1);

通过上面两个公式相减我们可以得到：f(n) = 2 * f(n-1)

---

（2）思路二 

当然这里也可以用非递归的方式来实现：
f(1) = 1 = 2⁰
f(2) = 1 + f(1) = 2 = 2¹
f(3) = 1 + f(2) + f(1) = 4 = 2²
f(4) = 1 + f(3) + f(2) + f(1) = 8 = 2³
...
f(n) = 2⁽ⁿ⁻¹⁾
这里可以使用函数 pow(2，n -1)，要记得加上头文件 <math.h>。也可以用 << 来表示。

---

2、代码 

#include<stdio.h>

int frog_jump_step(int n)
{
	if (n == 1)
	{
		return 1;
	}
	return 2 * frog_jump_step(n - 1);
}

int main()
{
	int n = 0;
	scanf("%d", &n);

	int way = frog_jump_step(n);
	printf("%d\n", way);

	return 0;
}

int frog_jump_step(int n)
{
    if (n == 1)
    {
        return 1;
    }
    return 1 << (n-1);
}

int main()
{
    int n = 0;
    scanf("%d", &n);

    int way = frog_jump_step(n);
    printf("%d\n", way);

    return 0;
}