目录
一、递归问题
1、斐波那契数列
2、汉诺塔问题
3、全排列问题
4、整数划分问题
二、递归式求解
1、代入法
2、递归树法
3、主定理法
三、 分治问题
1、二分搜索
2、大整数乘法
一、递归问题
1、斐波那契数列
斐波那契数列不用过多介绍,斐波那契提出的繁殖兔子问题。
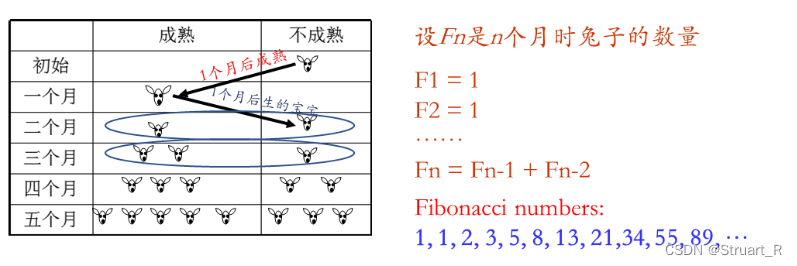
斐波那契递推式如下:
斐波那契代码:
//斐波那契数列
import java.util.Scanner;
public class Fibonacci {
public static void main(String [] args)
{
int input=new Scanner(System.in).nextInt();
System.out.println(factorial(input));
}
public static int factorial(int n)
{
if(n==0||n==1)
return 1;
else{
return factorial(n-1)+factorial(n-2);
}
}
}
2、汉诺塔问题
汉诺塔问题,也是一个经典问题。一般分为三个步骤:
(1)把n-1个盘子从A柱移到B柱
(2)把最底层1个盘子从A柱移到C柱
(3)把B柱n-1个盘子移到C柱。

完整代码:
package RecursionAndDivide;
import java.util.Scanner;
public class Hanoi {
public static void main(String[] args)
{
int input=new Scanner(System.in).nextInt();
move(input,'A','B','C');
}
public static void move(int n,char a,char b,char c)
{
if(n==1)
System.out.println(a+"->"+c); //
else {
move(n-1,a,c,b); //n-1个从a移到b
move(1,a,b,c); //底层1个从a移到c
move(n-1,b,a,c); //n-1个从b移到c
}
}
}3、全排列问题
使用递归的方式输出数组中的全排列,步骤如下:
(0)判定是否数组中仅有一个数,那么输出该排列形式。(请注意,k作为固定头,在每一层进行修改排列顺序的头部)
(1)首先将第一个数与后面的每一个数进行交换(这是一个k到m的循环)。得到:
1,2,3,4,...,n
2,1,3,4,...,n
3,1,2,4,...,n
(2)计算除第一个数以外后面的全排列。
(3)交换第一个数与刚刚那个数,使数组恢复。
k作为固定头,m作为尾,一直不改变,i作为固定头与循环中交换的数的索引。固定头依赖于第几层递归,不同的递归只会改变数组排列的方式,不会改变长度,而尾不动,所以每次输出只需要输出0到m索引的数组数,也就是所有数组的数。
完整代码:
//全排列问题
public class Permutations {
public static void main(String [] args)
{
int []list={1,2,3,4,5};
int k=0;int m=list.length-1;
Perm(list,k,m);
}
//产生全排列
public static void Perm(int []list,int k,int m)
{
if(k==m)
{
for(int i=0;i<=m;i++)
System.out.print(list[i]);
System.out.println();
}
else{
for(int i=k;i<=m;i++)
{
swap(list,i,k);
Perm(list,k+1,m);
swap(list,i,k);
}
}
}
//交换数组中两个元素
public static void swap(int []list,int i,int k)
{
int temp=list[i];
list[i]=list[k];
list[k]=temp;
}
}
4、整数划分问题

整数划分问题就是把一个正整数拆分成若干个正整数相加的所有方式,也可以使用递归来求解。定义p(n)为正整数n的划分总个数,q(n,m)为正整数n划分为最大值为m的划分总个数。
有以下递归式成立:
完整代码:
public class IntegerDivide {
public static void main(String[] args)
{
System.out.println(q(6,6));
}
public static int q(int n, int m)
{
if((n==1)||(m==1)) //且和或一样,或的话出现q(1,2)会执行条件2,返回q(1,1)
return 1;
if(n<m)
return q(n,n);
if(n==m)
return 1+q(n,n-1);
return q(n,m-1)+q(n-m,m);
}
}二、递归式求解
1、代入法
一般来说如果递归式成倍数下降,可以n取指数形式,平衡递归式的麻烦。换元求解就是不断回带递归式,最后得到T(1)项忽略,其他换元回变量n的项。

2、递归树法
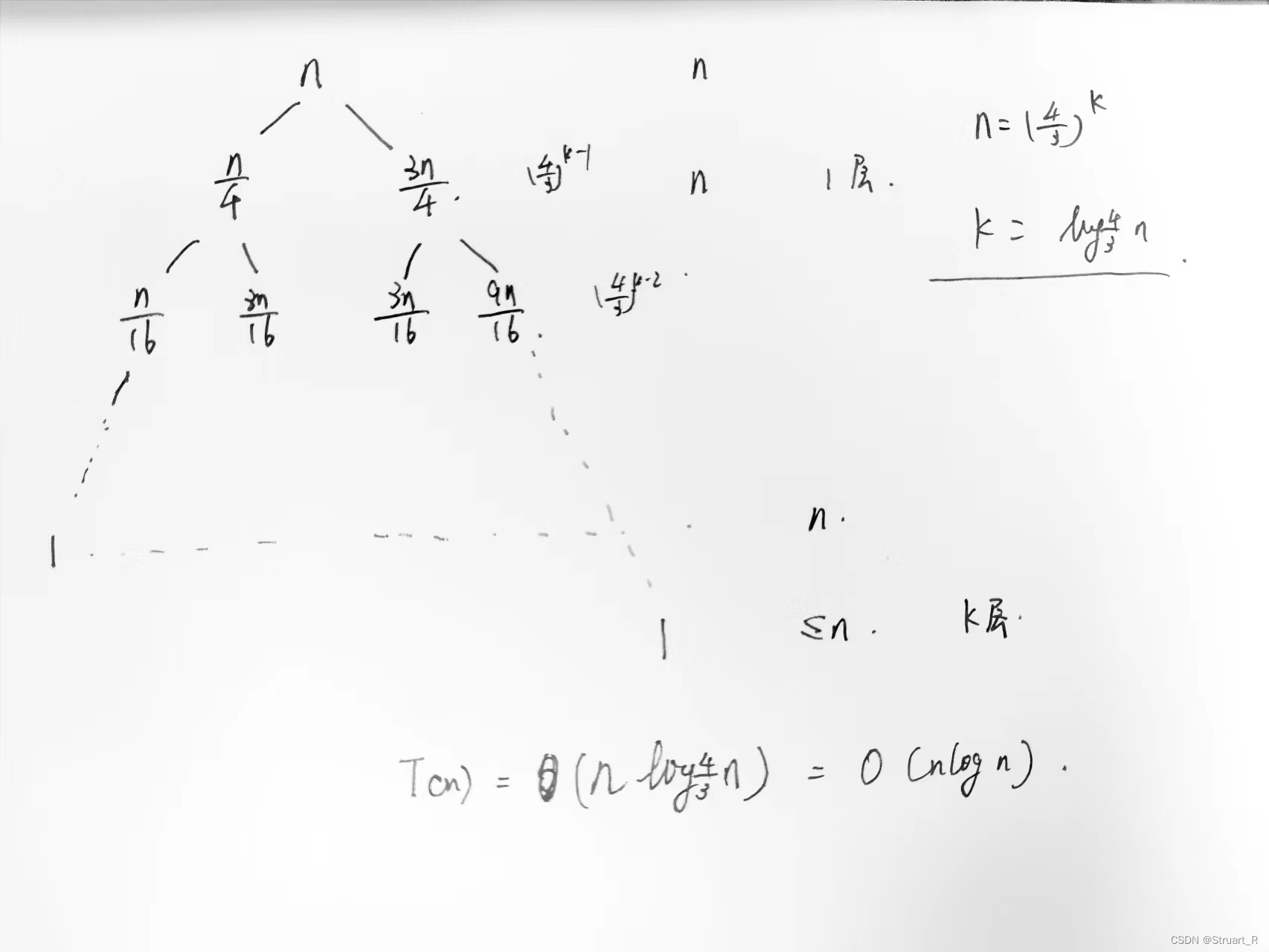
递归树法就是将常数项逐层展开成树叶子结点的形式,并将每一层的量相加的总和为递归式的解。如下面这个题,根节点就是递归式中的常数项n-1,每一层叶子点个数就是子递推式的系数为2,叶子结点的量只用n/2换元上一节点的量,得到n/2-1,以此类推,那么递推树如下。

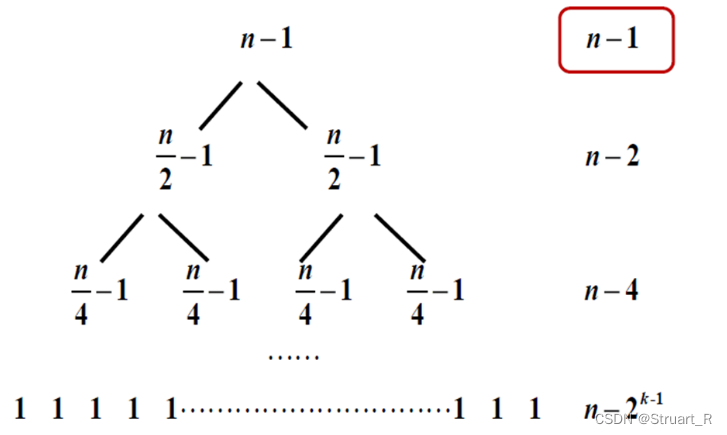
计算递推式每一层的和,注意最后一层以1为结束,当使用替代时,请注意层数变化,最后一层是
。那么总和如下,记得要用n替换k:
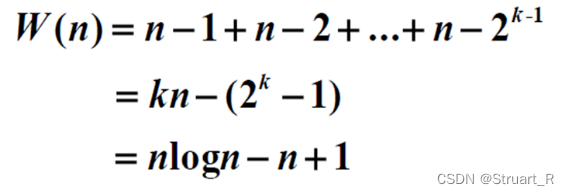
对于这一类递归树有偏重的题,可以参照下面这个做法,找到最慢下去的叶节点路线,就是大O的复杂度。
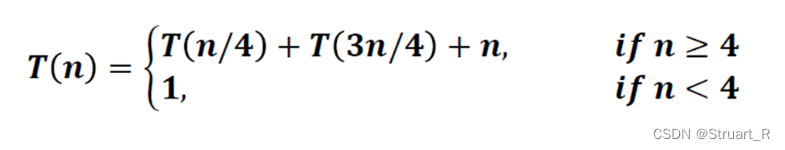
3、主定理法
主定理方法有一定局限性,最没有局限性的是代入法,但是很麻烦。

三、 分治问题
1、二分搜索
二分搜索原理:
(1)初始数组是已经排好序的,目的是某个数值是否存在,并找到他的索引,否则返回-1。
(2)大循环满足左值小于等于右值,每次取中间值,判断中间值是否为给定数值,若是返回索引。
(3)判断是否小于中间值,若是右值等于mid-1,判断是否大于中间值,若是左值等于mid+1。
(4)如果不满足循环条件,还没有找到给定值,那么返回-1。
二分搜索算法的复杂度为O(logn),应该建立在已排好序的数组上,如果为了搜索而去排序,复杂度就大大提升了。
//二分搜索
public static int Search(int arr[],int x,int n)
{
int left=0;int right=n-1;
while(left<=right)
{
int mid=(left+right)/2;
if(x==arr[mid])
return mid;
if(x>arr[mid])
left=mid+1;
else
right=mid-1;
}
return -1;
} 2、大整数乘法
由于大整数本身就会出现精度丢失问题,另外乘积数过大也会出现数值溢出的问题。所以可以用数组存储大整数进行两个数组之间的乘法。
另外高复杂度O(mn)也是不能忽视的问题,可以通过大整数拆成两段,将中间二次计算的环节存入内存,来减少复杂度。
比如下图X和Y都为n为二进制整数,计算它们的乘积,可以拆分成两个相等的n/2位的结构。
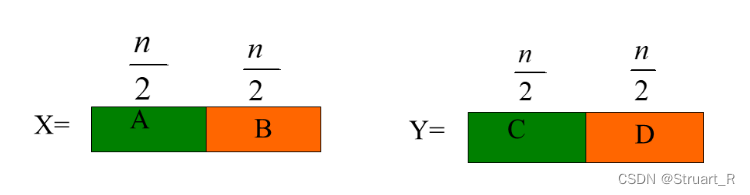
根据上面的式子改变,BD这一项就重复计算了,乘法计算的次数整体不变,但是BD可以不用二次计算了,这样就可以减少一次乘法计算,6次乘法变为5次乘法。 复杂度相比于也有所降低。
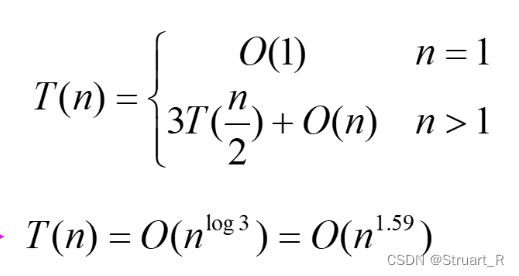
相类似的,矩阵乘法也可以用这种方式降低时间复杂度,成为Strassen矩阵乘法。