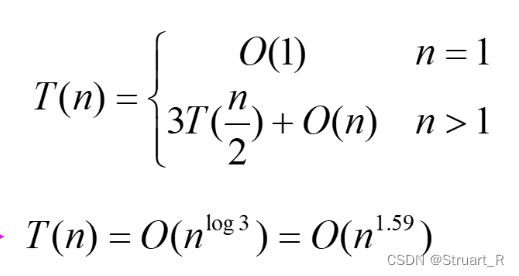目录
一. 冒泡排序
基本思想
代码实现
时间和空间复杂度
稳定性
二. 快速排序
基本思想
代码实现
hoare法
挖坑法
前后指针法
时间和空间复杂度
稳定性
一. 冒泡排序
基本思想
冒泡排序是一种交换排序。两两比较数组元素,如果是逆序(即排列顺序与排序后的顺序相 反)就交换,直到所有元素都有序为止。
方法步骤:
① 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
② 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后 的元素会是最大的数。
③ 针对所有的元素重复以上的步骤,除了最后一个。
④ 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
图示

代码实现
//冒泡排序
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
int flag = 0; //作为判断是否交换的标志
for (int j = 1; j < n - i; j++)
{
if (a[j-1] > a[j])
{
flag = 1;
int tmp = a[j-1]; //交换
a[j-1] = a[j];
a[j] = tmp;
}
}
if (flag == 0)
break;
}
}
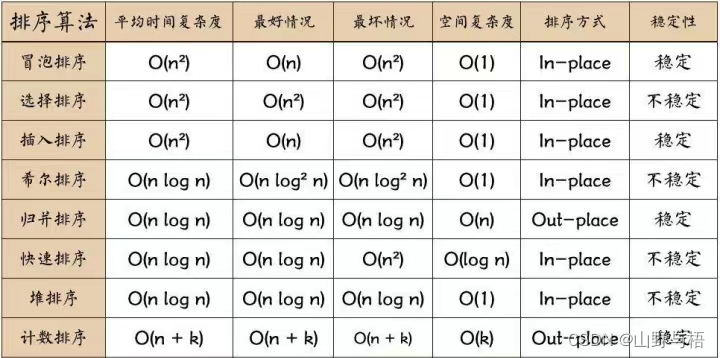
时间和空间复杂度
若初始序列为正序序列,则只需进行一趟排序,在排序过程中进行n-1次比较,不移动元素;若初始序列为逆序序列,则需进行n-1趟排序,n(n-1) / 2次比较,每次比较都需要移动 3 次,移动次数为 3n(n-1) / 2.
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性
冒泡排序:稳定排序
二. 快速排序
基本思想
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
方法步骤:
-
从数列中挑出一个元素,称为 "基准"(pivot);
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
图示
代码实现
hoare法
思想方法:
定义两个指针 left 和 right,分别指向左边和右边,左指针从左向右找大( 大于pivotkey),右 指针从右向左找小(小于pivotkey),左大右小就交换,相遇时与基准值交换
图解:

int PartSort(int* a, int left, int right) //给数组分区,返回枢轴元素下标
{
int pivotkey = left;
while (left < right)
{
//右边找比pivotkey小的
while (left < right && a[right] >= a[pivotkey])
right--;
//左边找比pivotkey大的
while (left < right && a[left] <= a[pivotkey])
left++;
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[pivotkey]); //把记录的枢轴元素,交换到枢轴位置
return left; //返回枢轴所在的位置下标
}
挖坑法
思想方法:
定义两个指针 left 和 right,分别指向左边和右边,先将第一个数据元素放在临时变量 pivotkey 中,形成一个坑位;让右指针先走,当指向的值小于 pivotkey 就停下,形成新的坑位;让左指针走,当指向的值大于 pivotkey 就停下,使其形成此次的新坑位,直到两指针相遇,把pivotkey的值放入坑中。
图解:

int PartSort(int* a, int left, int right) //给数组分区,返回枢轴元素下标
{
int pivotkey = a[left]; //保存第一个数据元素的值
while (left < right)
{
while (left < right && a[right] >= pivotkey) //找小
{
right--;
}
a[left] = a[right]; //右边形成新的坑
while (left < right && a[left] <= pivotkey) //找大
{
left++;
}
a[right] = a[left]; //左边形成新的坑
}
a[left] = pivotkey;
return left;
}
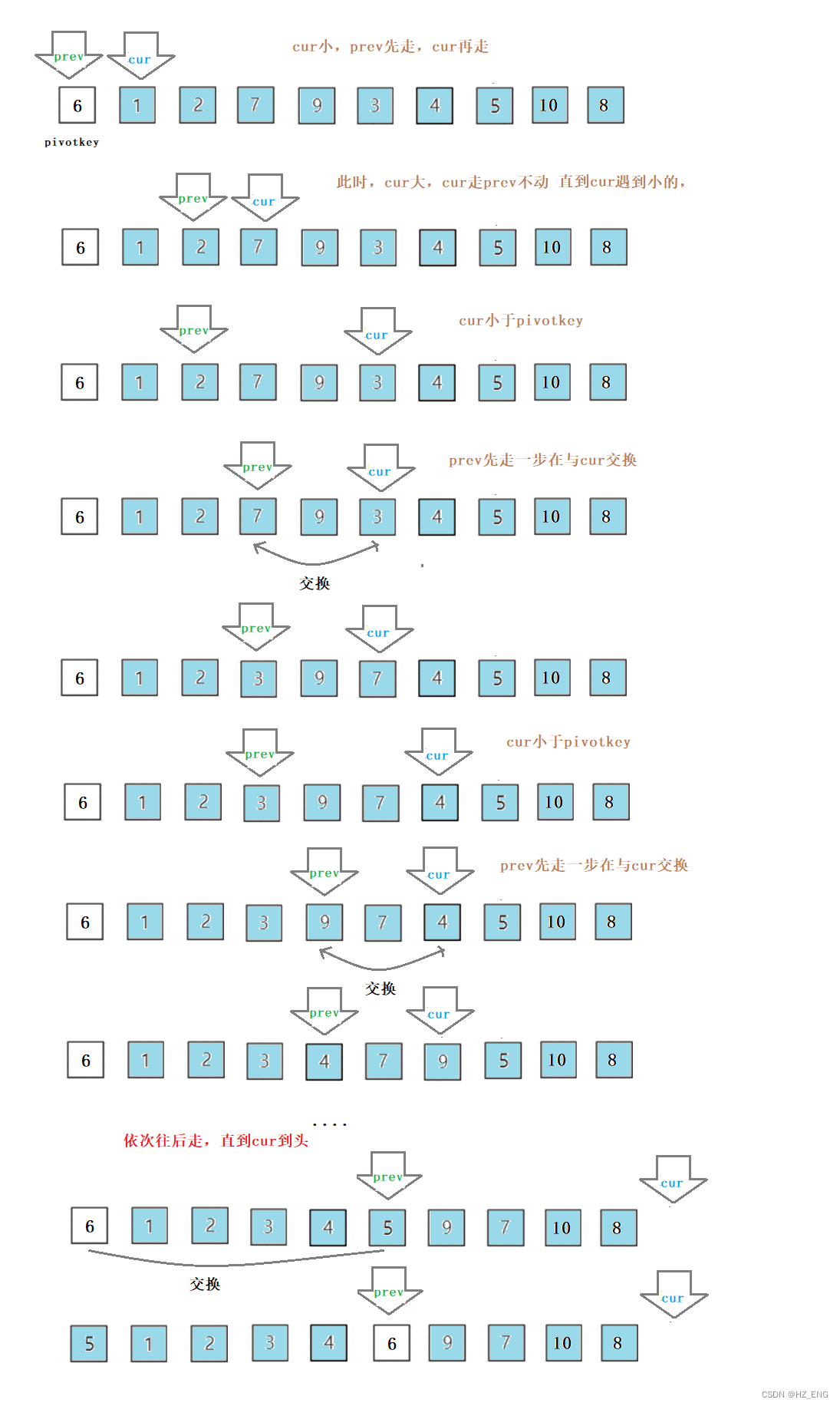
前后指针法
思想方法:
定义两个指针 prev 和 cur ,初始时,prev指针指向序列开头,cur指针指向prev指针的后一个位置;cur的值与pivotkey的值比较,cur的值小,prev先后移一步,cur再后移;当cur的值大时,就prev的值与cur的值交换;直到cur为空时,prev的值与pivotkey的值交换。
图解:
int PartSort(int* a, int left, int right) //给数组分区,返回枢轴元素下标
{
int prev = left;
int cur = left + 1;
int pivotkey = left;
while (cur <= right)
{
if (a[cur] < a[pivotkey] && ++prev != cur)
Swap(&a[cur], &a[prev]);
cur++;
}
Swap(&a[pivotkey], &a[prev]);
return prev;
}
时间和空间复杂度
在最优情况下,partition每次都划的很均匀,此时时间复杂度为O(nlogn);平均情况下,其时 间复杂度也为O(nlogn)。在最坏的情况下,待排序的序列为正序或逆序时,递归树是一棵斜树, 此时,快速排序会堕落为冒泡排序,其时间复杂度为O(n^2),不过可以通过优化,使其提升为O(nlogn),总的来说还是O(nlogn)。
空间复杂度,主要是递归造成的栈空间的使用,最好情况及平均情况下,树的递归深度为logn,空间复杂度均为O(logn);最坏情况,空间复杂度为O(n).
时间复杂度:O(nlogn)
空间复杂度:O(logn)
稳定性
由于元素的比较和交换是跳跃进行的,因此
快速排序:不稳定排序