目录
一、定义
二、B树的核心特性
1、B树各个结点的子树数和关键字数
2、子树高度
3、关键字的值
4、B树高度
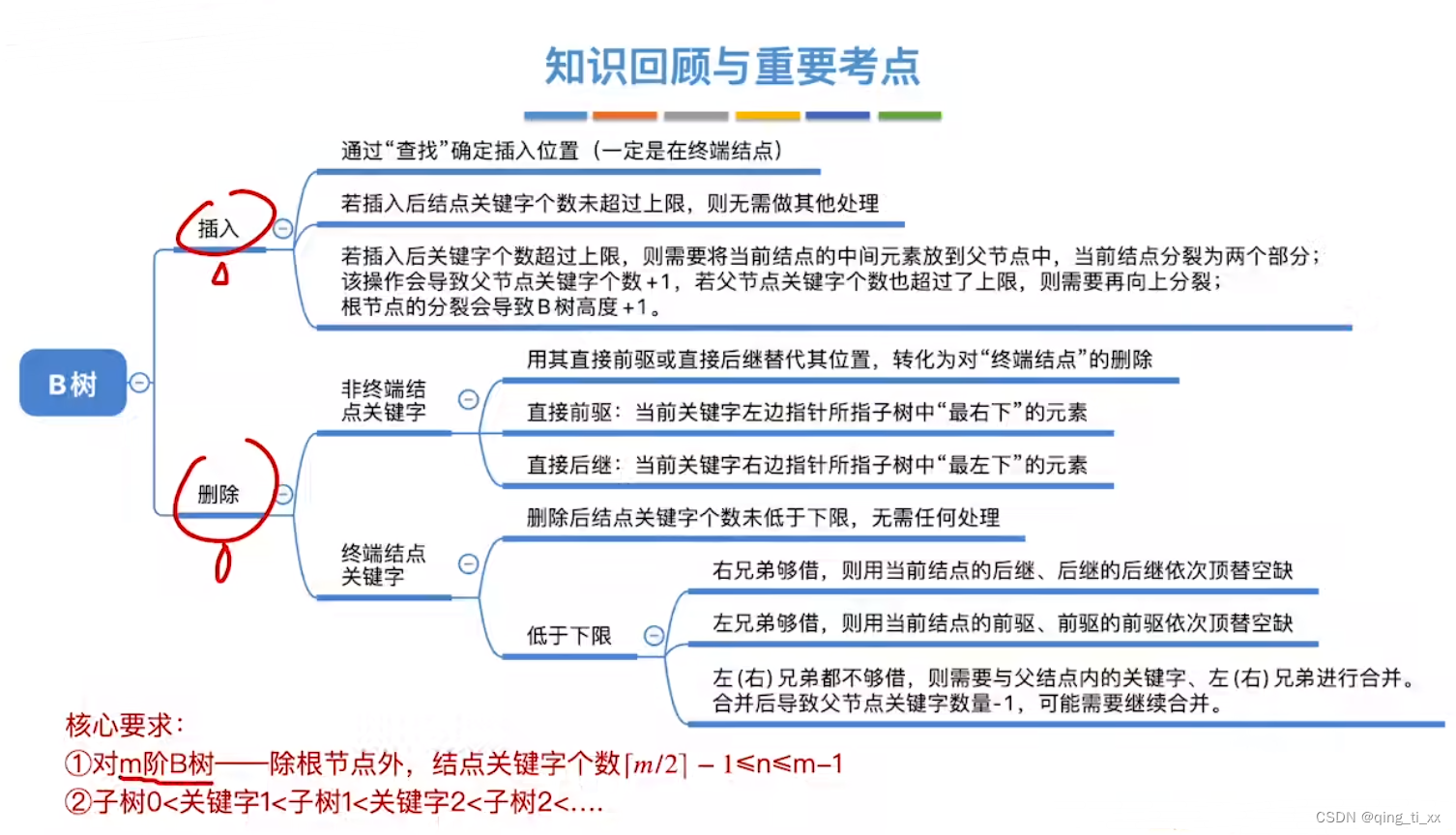
三、B树的插入
四、B树的删除
一、定义
B树,又称多路平衡查找树,B树中所有结点的孩子个数的最大值称为B树的阶,通常用m表示。
一棵m阶B树或为空树,或为满足如下特性的m叉树:
1)树中每个结点至多有m棵子树,即至多含有m-1个关键字。
2)若根结点不是终端结点,则至少有两棵子树。
3)除根结点外的所有非叶结点至少有「m/2]棵子树,即至少含有「m/2]-1个关键字。
4)所有的叶结点都出现在同一层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失败结点,实际上这些结点不存在,指向这些结点的指针为空)。
注意:在B树中,所有子树的高度都必须相同,也就是说它们的平衡因子都为0,这样才能保证B树的查找效率。
二、B树的核心特性
1、B树各个结点的子树数和关键字数
根节点的子树数∈[2, m],关键字数∈[1, m-1]。
其他结点的子树数∈[[m/2], m];关键字数∈[[m/2]-1, m-1]
2、子树高度
对任意结点,其所有子树高度都相同。
3、关键字的值
左<中<右
4、B树高度
含n个关键字的m叉B树,
三、B树的插入

四、B树的删除






![[C++_containers]10分钟让你掌握vector](https://img-blog.csdnimg.cn/2061eb2ab5e14341aee0189b14c35bbd.png)