课程地址和说明
Softmax回归p1
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
Softmax回归
虽然它名字叫作回归,但是它其实是分类问题



本节课的基础
想要学会本节课得需要一点基础,我真没看懂这节课讲的是什么,查了一些资料补了补基础
此处参考视频信息量 |熵 | 交叉熵 |KL散度 (相对熵)|交叉熵损失函数
信息量(Amount of Information)
定义
事件包含的信息量大小(事件发生的难度有多大)
- 小概率事件,它发生的难度比较大,所以有较大的信息量;
- 大概率事件,它发生的难度比较小,所以有较小的信息量。
【例】

公式
信息量的公式为:
I
(
x
)
:
=
(人为定义的)
l
o
g
2
1
P
(
x
)
=
−
l
o
g
2
P
(
x
)
I(x):=(人为定义的)log_{2}{\frac{1}{P(x)}}=-log_{2}{{P(x)}}
I(x):=(人为定义的)log2P(x)1=−log2P(x)

性质
对于独立事件
A
,
B
A,B
A,B,其概率为
P
(
A
B
)
=
P
(
A
)
P
(
B
)
P(AB)=P(A)P(B)
P(AB)=P(A)P(B),而两个事件同时发生的信息量等于两个事件的信息量相加,即:
I
(
A
B
)
=
I
(
A
)
+
I
(
B
)
I(AB)=I(A)+I(B)
I(AB)=I(A)+I(B)
例子

熵(Entropy)
定义

【注】期望就是加权和求出来的平均值,此处权值为概率
公式

作用

【注】左图,每个概率都相等,不确定哪个会更容易发生,而右图很容易确定。
例子

结论

交叉熵
定义

公式
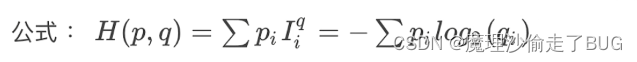
例子

结论


相对熵(KL散度)
KL散度以 Kullback 和Leibler的名字命名,也被称为相对嫡
作用
用于衡量2个概率分布之间的差异
公式
假设真实概率分布为
p
p
p、预测概率分布(估计概率分布)为
q
q
q
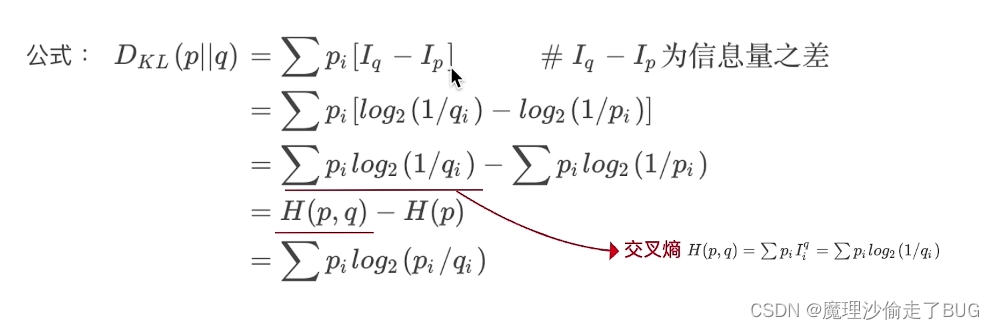
重要性质

交叉熵损失函数


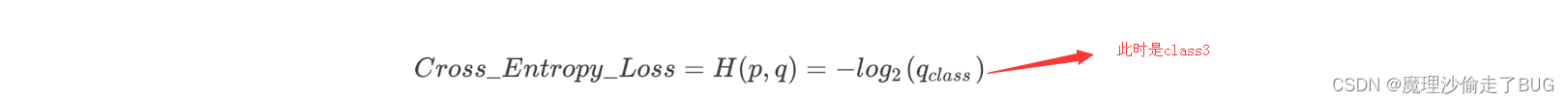
Softmax回归的基本原理
此处参考视频:softmax回归原理及损失函数-跟李沐老师动手学深度学习
Softmax回归也是和线性回归一样讲数字特征和权重做线性叠加,不同的是线性回归的输出是一个连续的值,但Softmax回归的输出是离散的值,并且其输出由线性回归中的一个变为了多个:
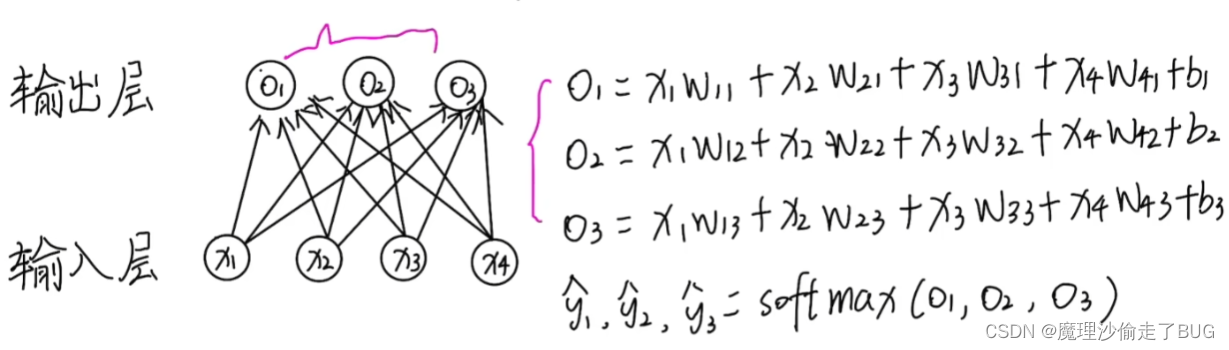
将特征和权重做叠加后用Softmax函数进行计算,将输出值
O
1
,
O
2
,
O
3
O_{1},O_{2},O_{3}
O1,O2,O3映射为0到1之间的数(即概率,
y
i
^
\hat{y_{i}}
yi^是概率值),公式如下:
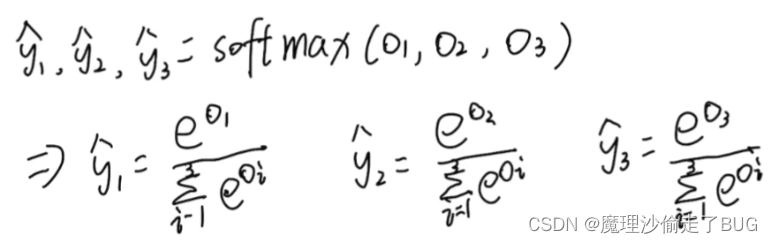
并且按此方法得到了一个概率分布,即预测值
y
1
^
,
y
2
^
,
y
3
^
,
.
.
.
\hat {y_{1}},\hat {y_{2}},\hat {y_{3}},...
y1^,y2^,y3^,...都为正值,并且它们的和为1
在实际操作中,我们选择
y
1
^
,
y
2
^
,
y
3
^
,
.
.
.
\hat {y_{1}},\hat {y_{2}},\hat {y_{3}},...
y1^,y2^,y3^,...中最大的预测值,找到最大的预测值所对应的类别标签即为我们预测的类别。
举个例子(下面认为输出类别是第二类):

以上就是Softmax回归的预测过程。
为了提高计算效率,我们将上面的数学公式形式化为线性代数语言:
-
单个样本的向量形式:
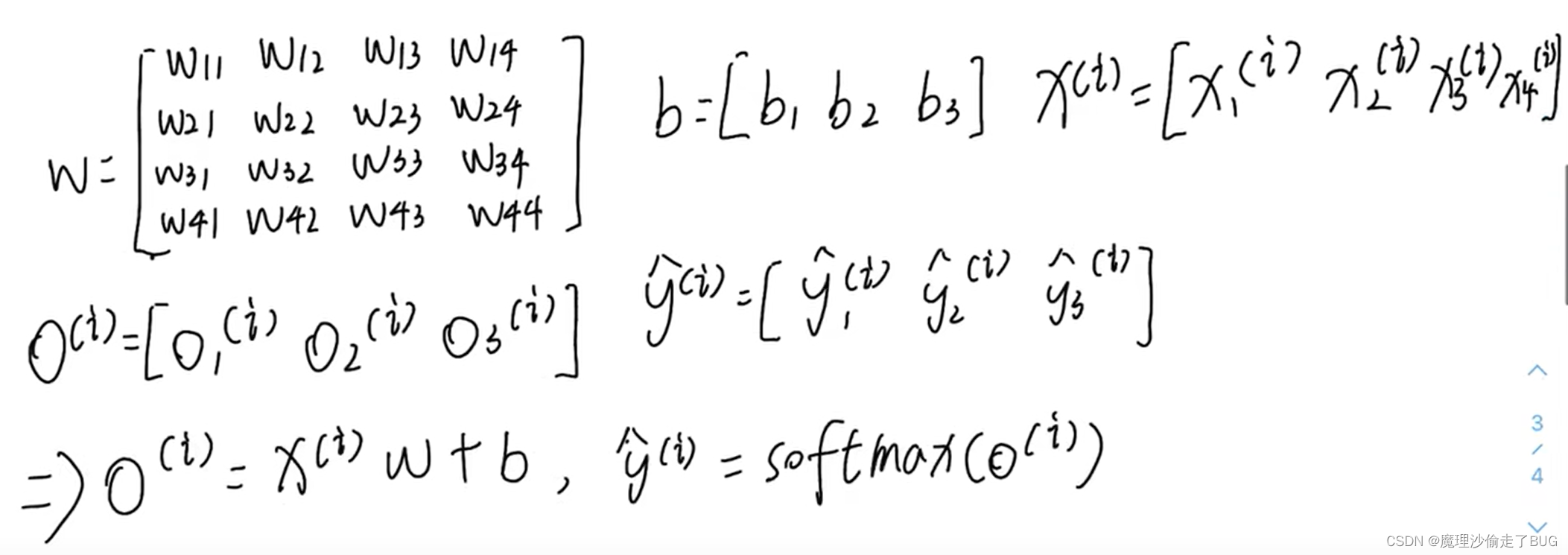
-
小批量样本的向量形式
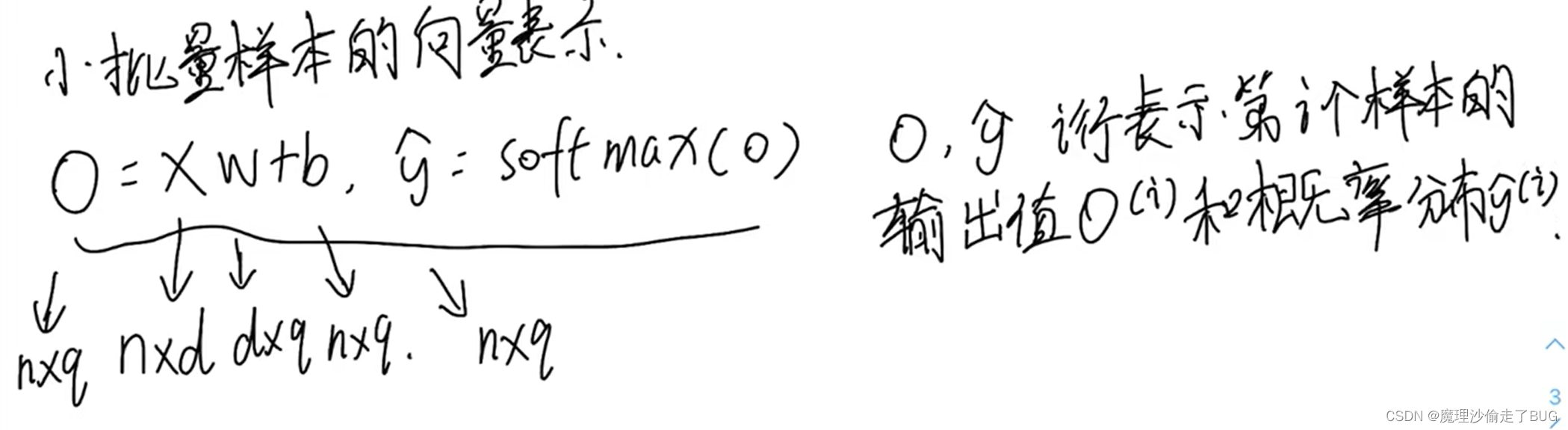
【注】如果行向量不能相乘或相加,默认取转置, n n n为 n n n个样本, d d d为数字特征的个数, q q q表示输出类别的个数
- 损失函数
对于概率分布问题,其损失函数一般为交叉熵损失函数:
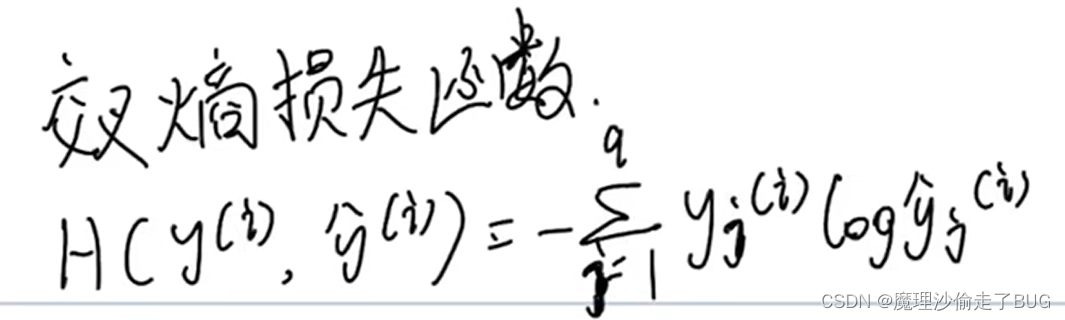

【注】有一个为1,其他为0,其他项目都没了
从回归到多类分类
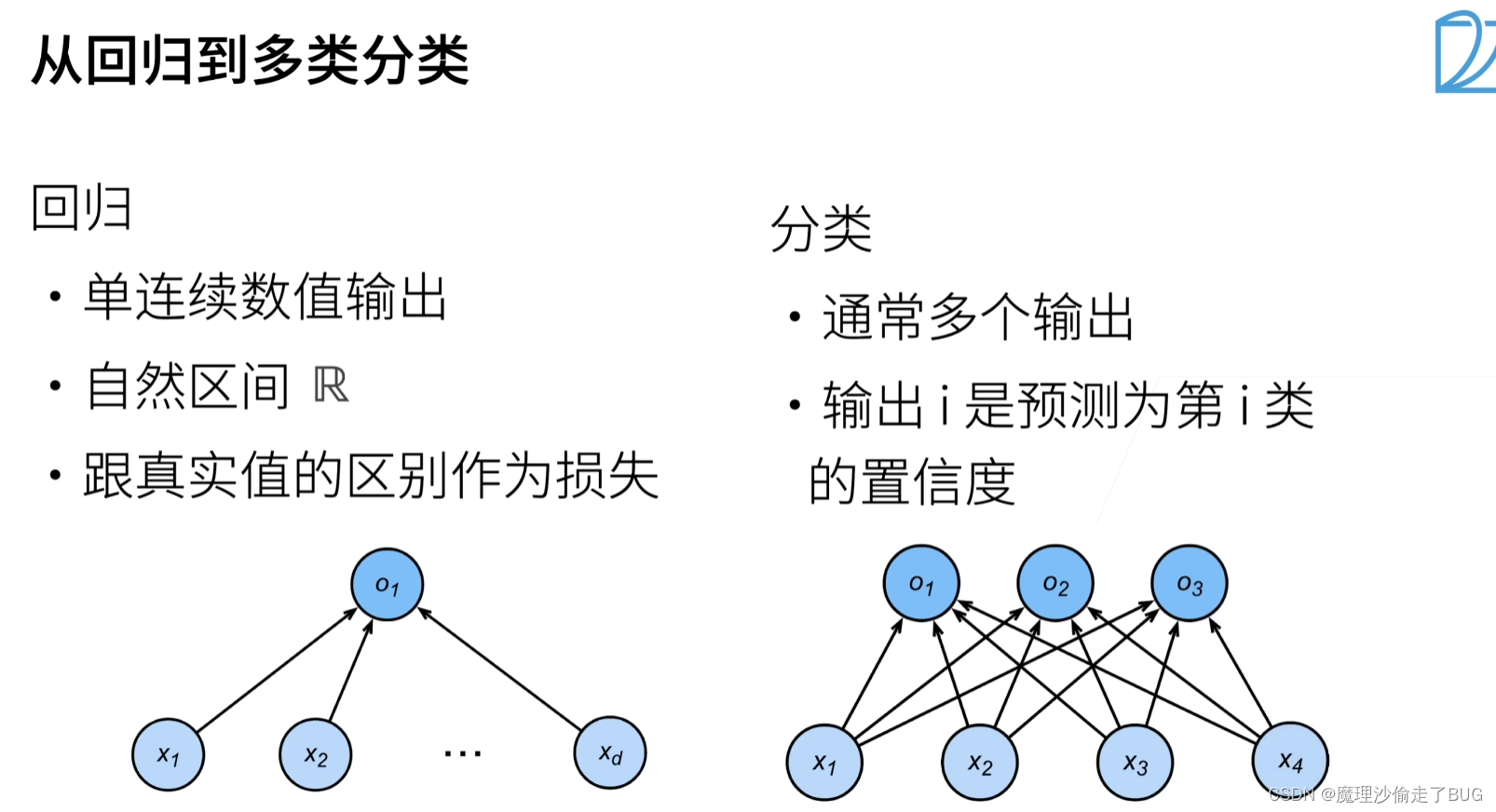
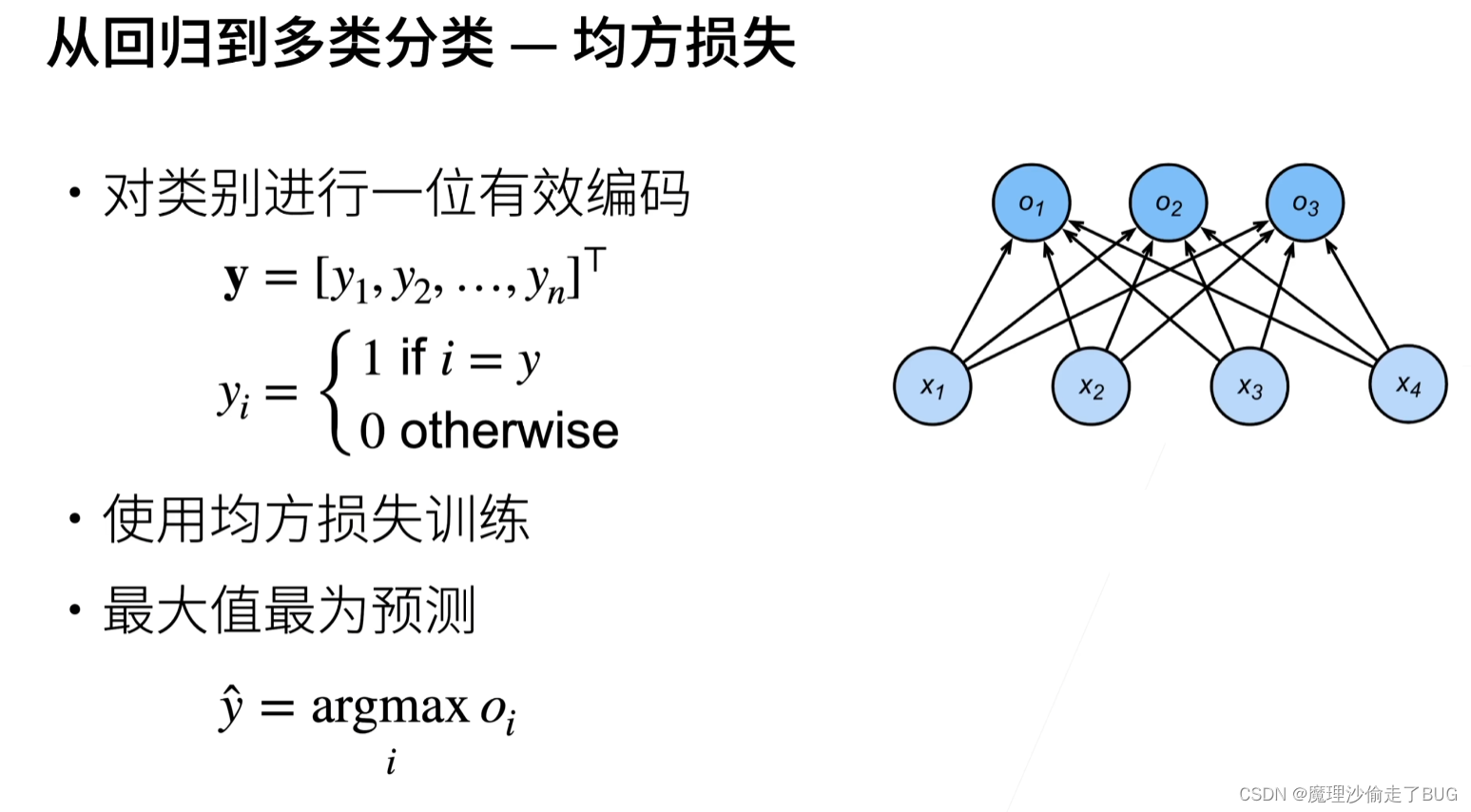
【注】
y
i
y_{i}
yi有一个为1,说明该输出结果属于第
i
i
i个类别。
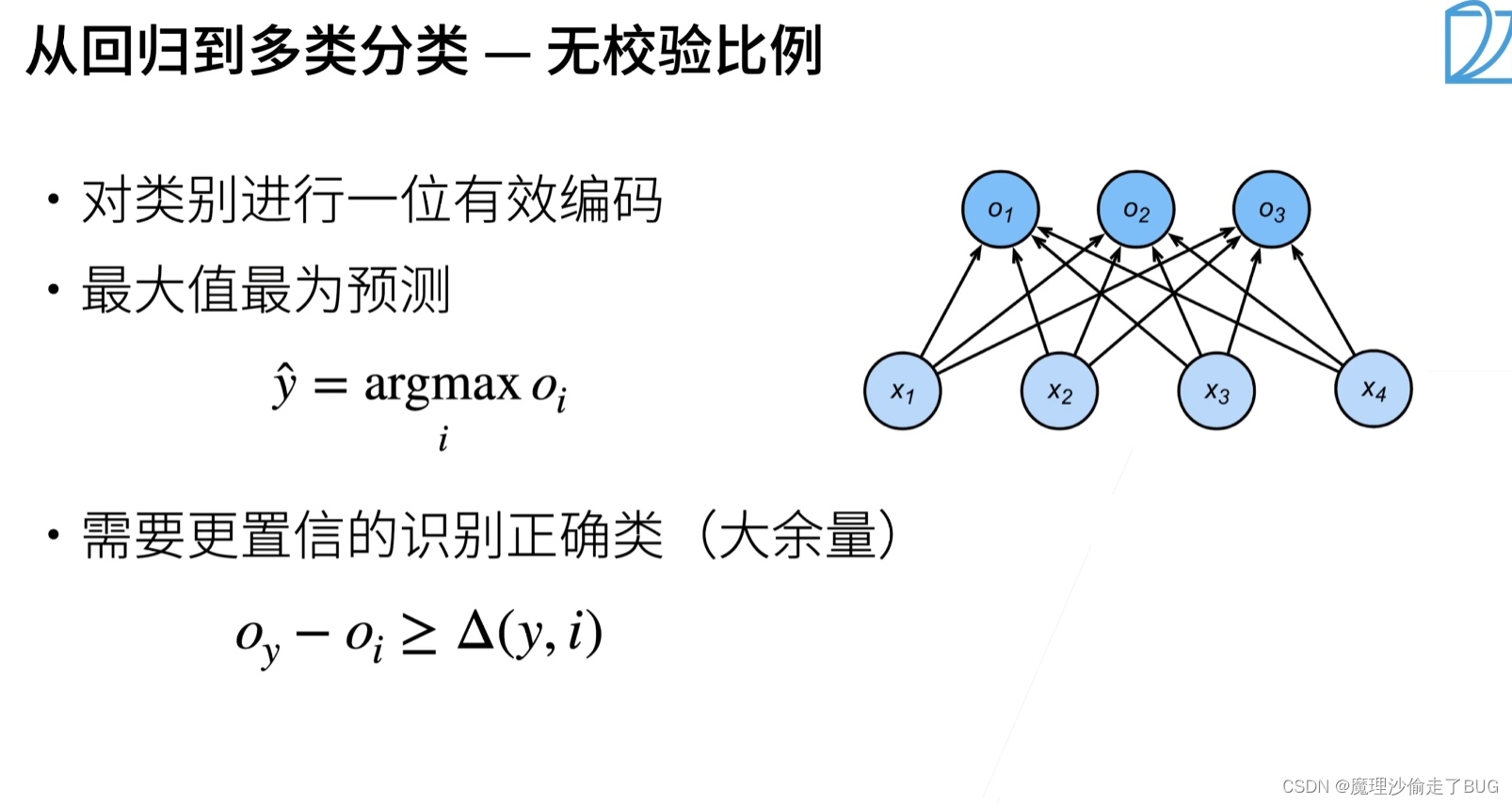
【注】正确类
O
y
O_{y}
Oy的置信度要远远大于其他非置信度的
O
i
O_{i}
Oi
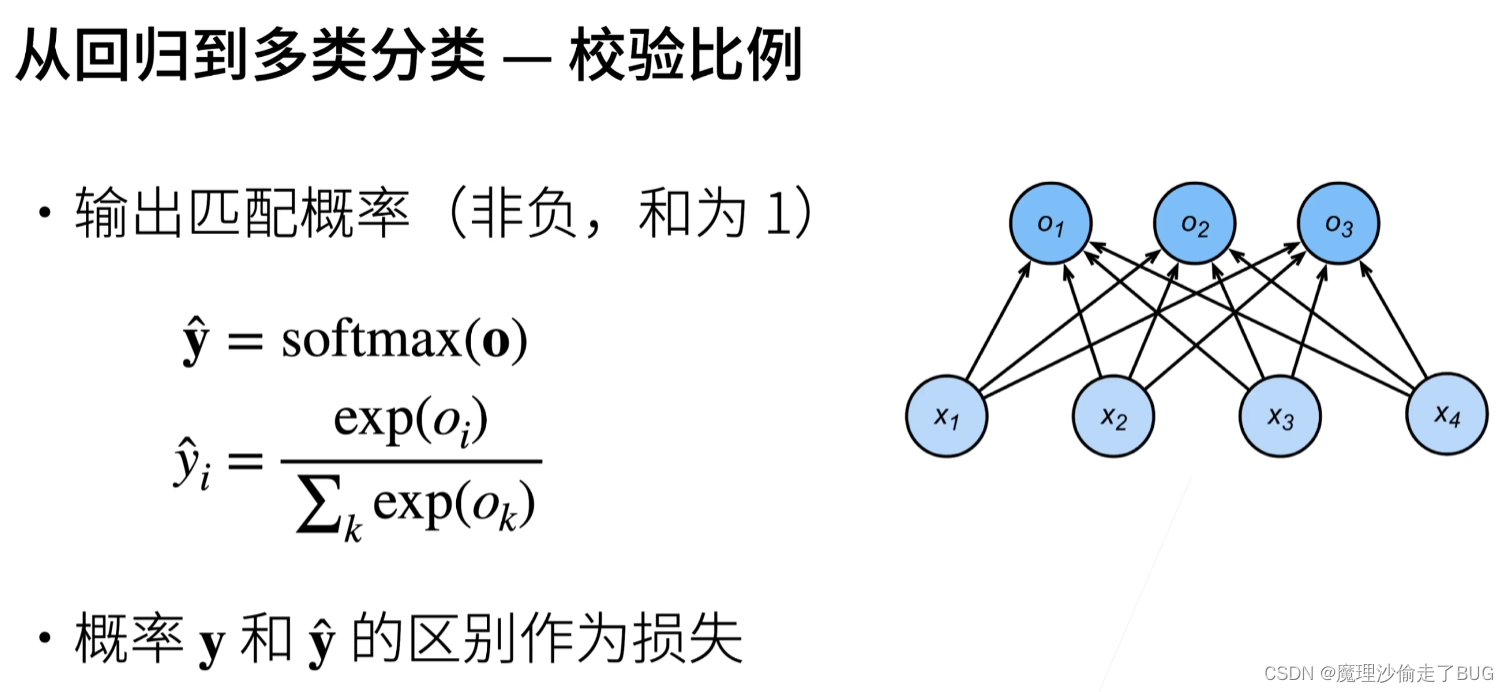
【注】
o
→
\overrightarrow{o}
o是一个长度为
n
n
n的向量,前文提到的
o
→
=
(
O
1
,
O
2
,
.
.
.
)
\overrightarrow{o}=(O_{1},O_{2},...)
o=(O1,O2,...),这其中每一个
O
i
O_{i}
Oi都是前文提到的线性回归。
比较两个概率之间的区别用交叉熵损失函数:

总结






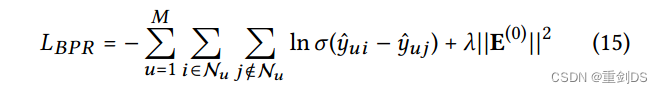





![[RCTF2015]EasySQL 二次注入 regexp指定字段 reverse逆序输出](https://img-blog.csdnimg.cn/ca94ca45f8ab42d9a462c2af77dc0ecd.png)