版本说明
当前版本号[20230926]。
| 版本 | 修改说明 |
|---|---|
| 20230926 | 初版 |
目录
文章目录
- 版本说明
- 目录
- 二分查找
- 基础版
- 算法描述
- 分步演示
- 情况一:能在有序数组找到待查值
- 情况二:不能在有序数组找到待查值
- 翻译成代码
- 基础版代码(包括测试类)
- 疑惑解答
- 基础版改良后代码
- 进阶版
- 改动地方
- 改动一:i 跟 j 的边界位置
- 改动二:while 的条件
- 改动三:if 判断中的 j 的边界问题
- 改动后代码
- 分步演示
- 改动地方的解释
- i 跟 j 的边界位置改动原因
- while 的条件改动原因
- if 判断中的 j 的边界问题改动原因
- 衡量算法好坏
- 时间复杂度
- 如何表示时间复杂度
- 大 O O O 表示法
- 渐进上界
- 常见大 O O O 表示法
- 渐进下界
- 渐进紧界
- 空间复杂度
- 二分查找性能
- 平衡版
- 算法题实战:力扣704 . 二分查找
二分查找
二分查找算法也称折半查找,是一种非常高效的工作于有序数组的查找算法。后续的课程中还会学习更多的查找算法,但在此之前,不妨用它作为入门。
基础版
需求:在有序数组 A A A 内,查找值 t a r g e t target target
- 如果找到返回索引
- 如果找不到返回 − 1 -1 −1
算法描述
| 前提 | 给定一个内含 n n n 个元素的有序数组 A A A,满足 A 0 ≤ A 1 ≤ A 2 ≤ ⋯ ≤ A n − 1 A_{0}\leq A_{1}\leq A_{2}\leq \cdots \leq A_{n-1} A0≤A1≤A2≤⋯≤An−1,一个待查值 t a r g e t target target |
| 1 | 设置 i = 0 i=0 i=0, j = n − 1 j=n-1 j=n−1 |
| 2 | 如果 i > j i \gt j i>j,结束查找,没找到 |
| 3 | 设置 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) , m m m 为中间索引, f l o o r floor floor 是向下取整( ≤ i + j 2 \leq \frac {i+j}{2} ≤2i+j 的最小整数) |
| 4 | 如果 t a r g e t < A m target < A_{m} target<Am 设置 j = m − 1 j = m - 1 j=m−1,跳到第2步 |
| 5 | 如果 A m < t a r g e t A_{m} < target Am<target 设置 i = m + 1 i = m + 1 i=m+1,跳到第2步 |
| 6 | 如果 A m = t a r g e t A_{m} = target Am=target,结束查找,找到了 |
分步演示
情况一:能在有序数组找到待查值
1、给定一个有序数组,并且在其下面标上下标。
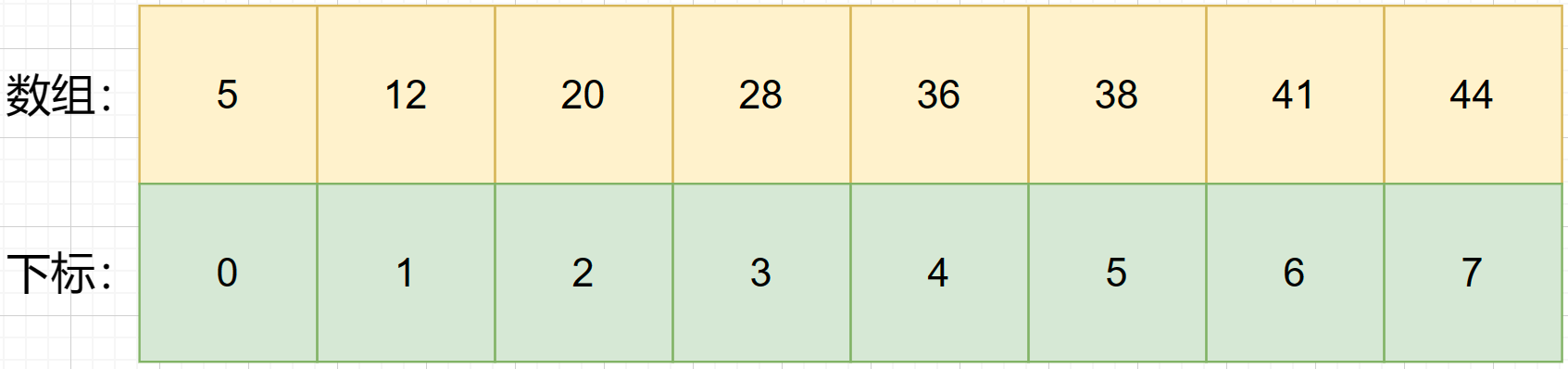
2、设置一个i值和一个j值,i从数组第0号元素左边开始检索,j从数组最后一个元素右边开始检索。
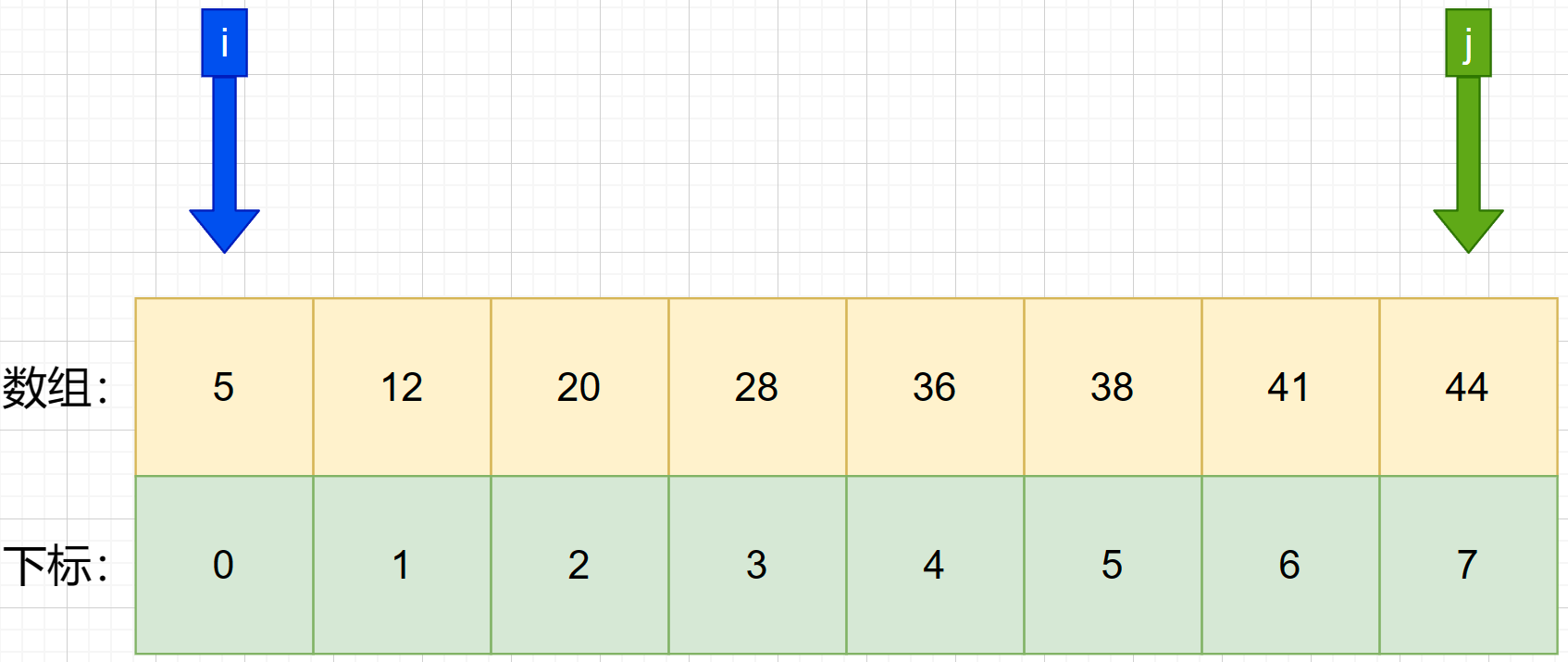
3、设定一个可以在数组中能找到的数值:36 作为待查值target。接着开始二分查找。首先找第一次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(0+7)/ 2 = 3.5 ,向下求值后可得m=3。
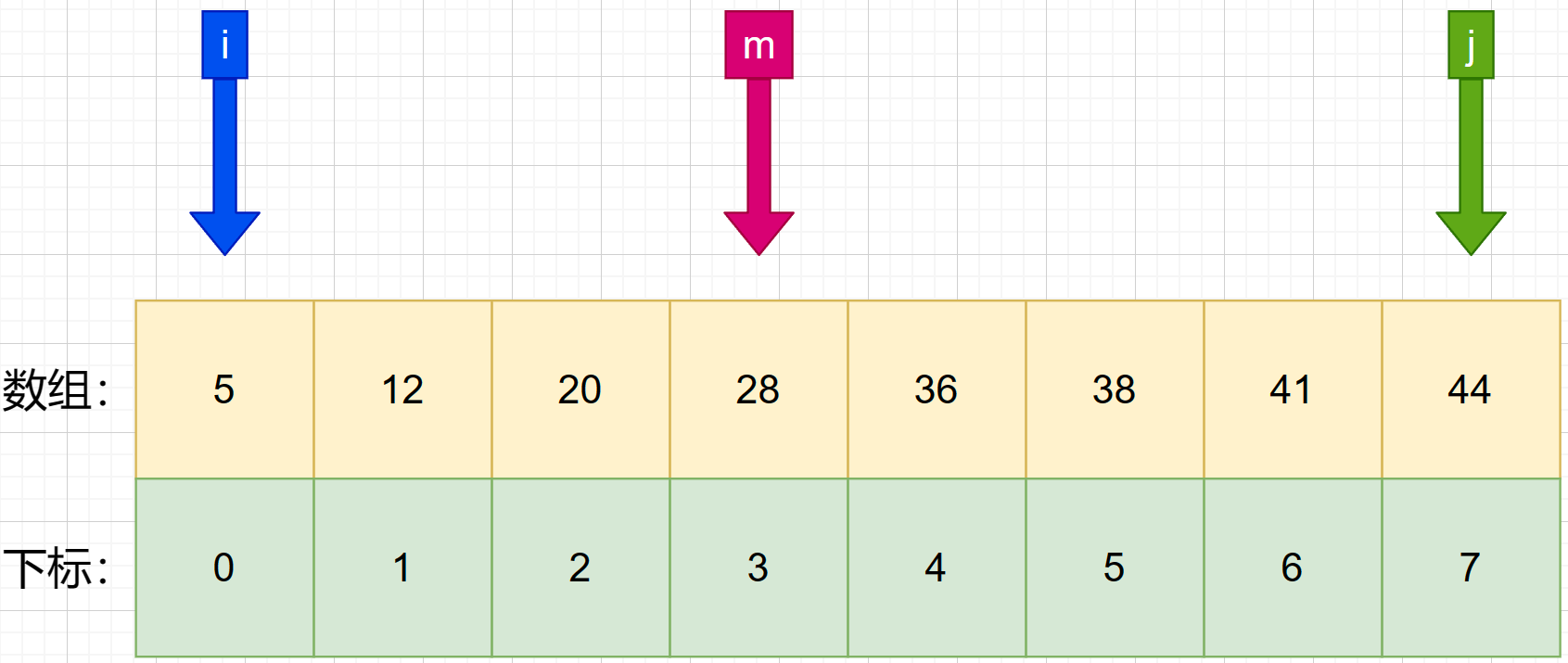
4、**判断第一次中间索引与待查值的大小。**发现 m 所对应的数为 28,小于待查值 36.就将 i 设置成 m+1 .
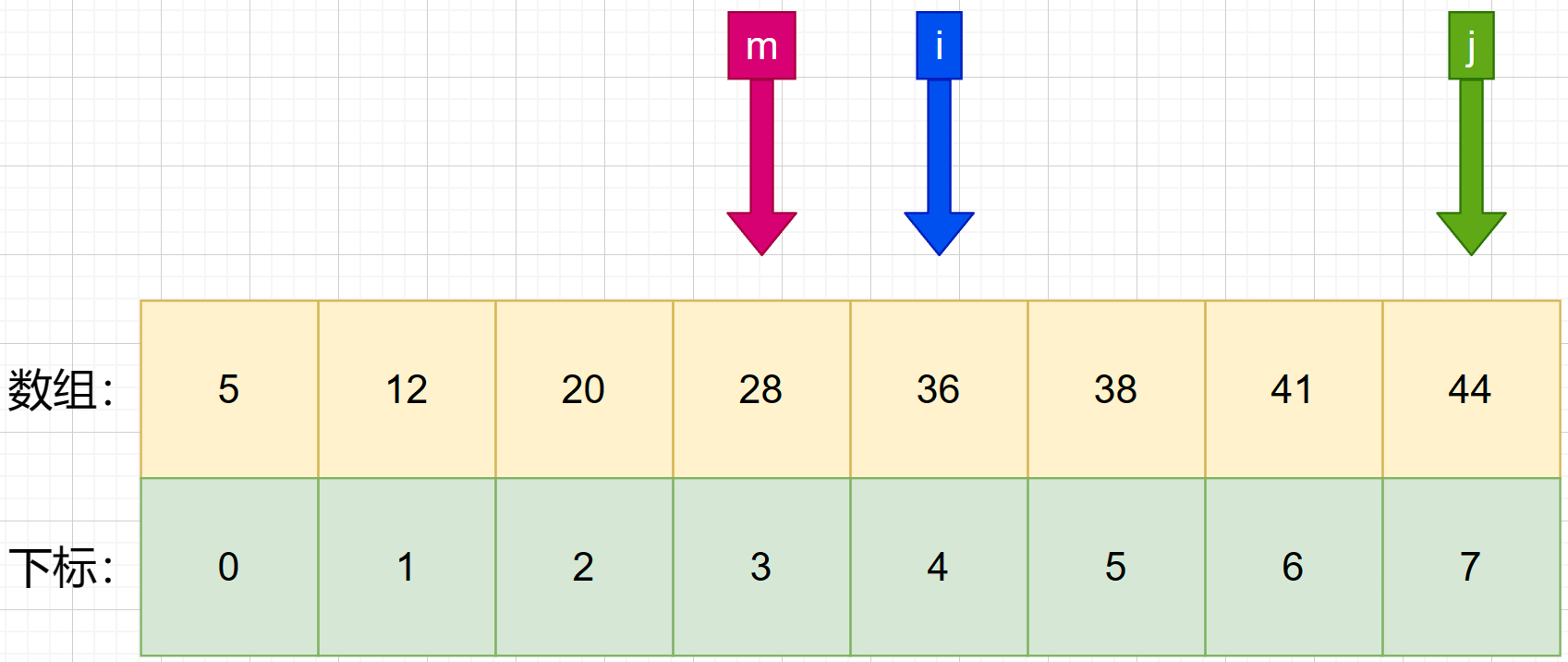
5、接着找第二次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(4+7)/ 2 = 5.5 ,向下求值后可得m=5。
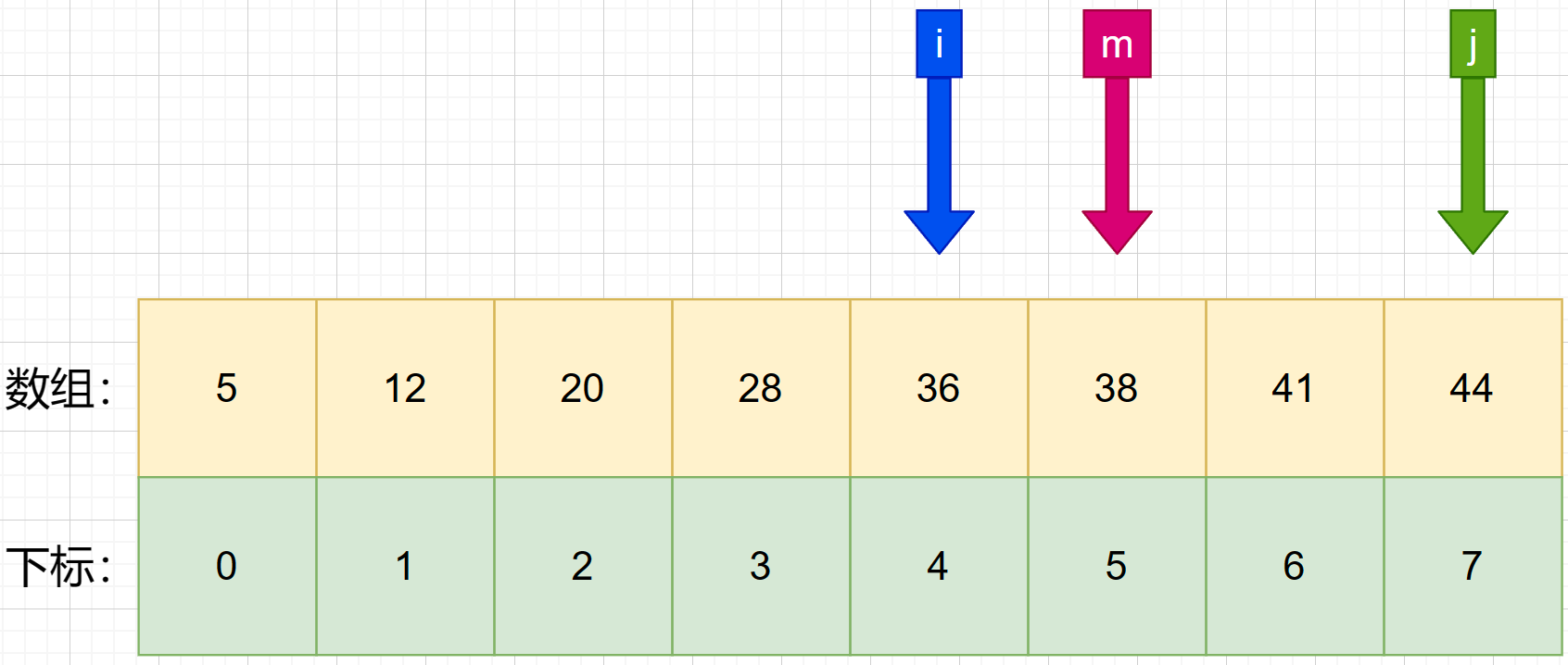
6、**判断第二次中间索引与待查值的大小。**发现 m 所对应的数为 38,大于待查值 36.就将 j 设置成 m-1 .
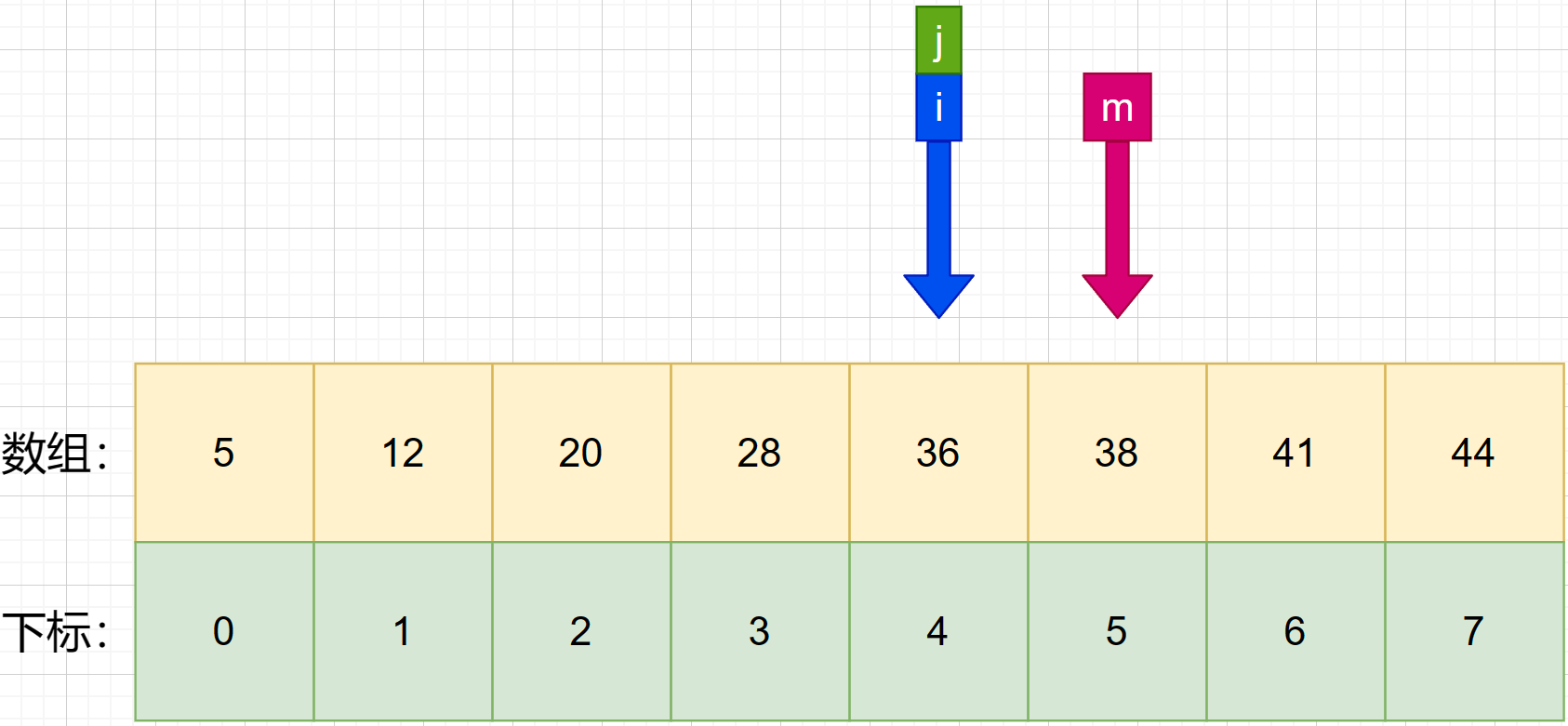
7、接着找第三次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(4+4)/ 2 = 4 .
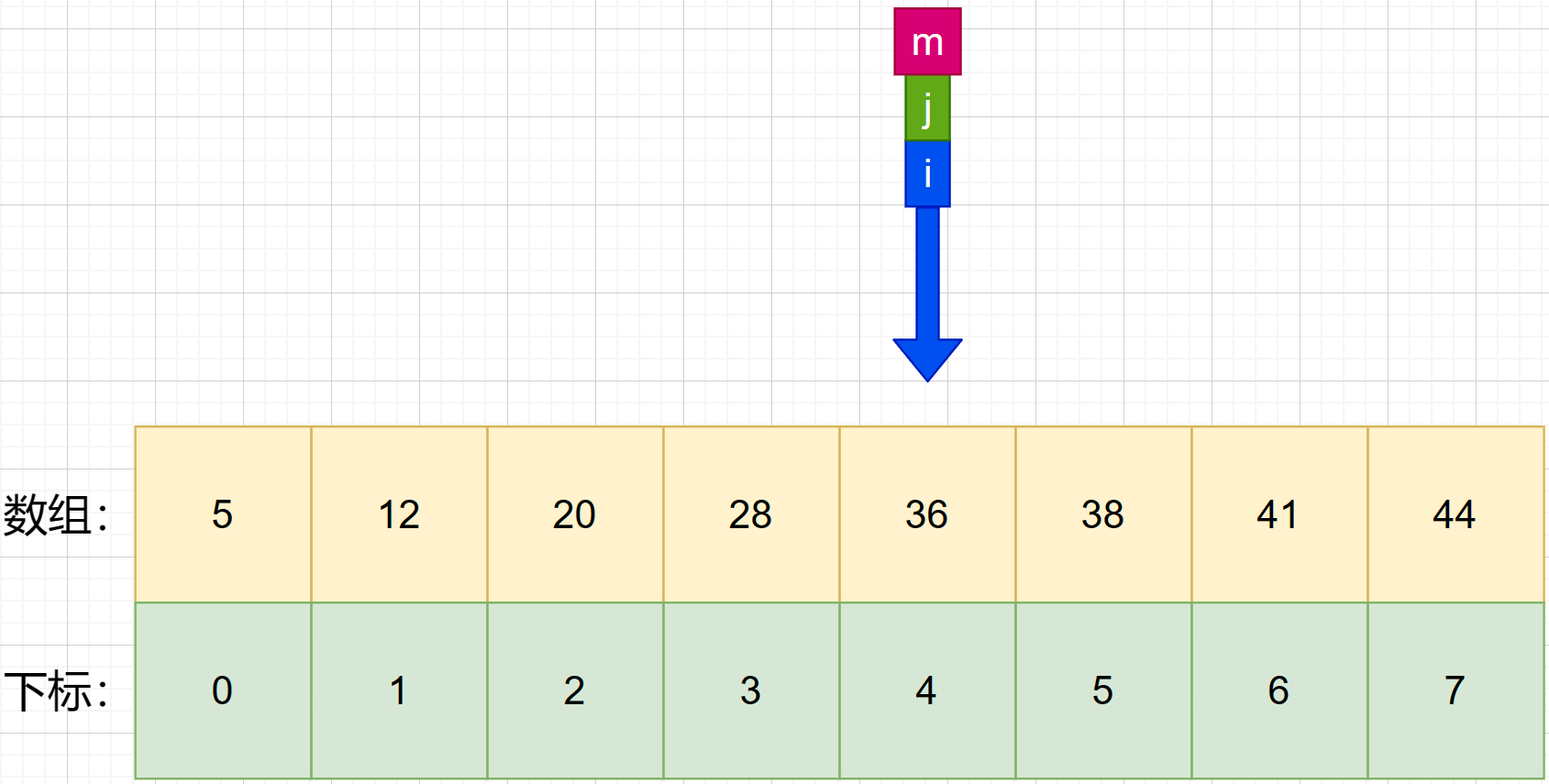
8、**判断第三次中间索引与待查值的大小。**发现 m 所对应的数为 36,等于待查值 36.到这里我们就通过二分查找找到了待查值。
情况二:不能在有序数组找到待查值
1、给定一个有序数组,并且在其下面标上下标。【与上同】

2、设置一个i值和一个j值,i从左边开始检索,j从右边开始检索。【与上同】

3、设定一个可以在数组中能呗找到的数值:26 作为待查值target。接着开始二分查找。首先找第一次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(0+7)/ 2 = 3.5 ,向下求值后可得m=3。【与上同】
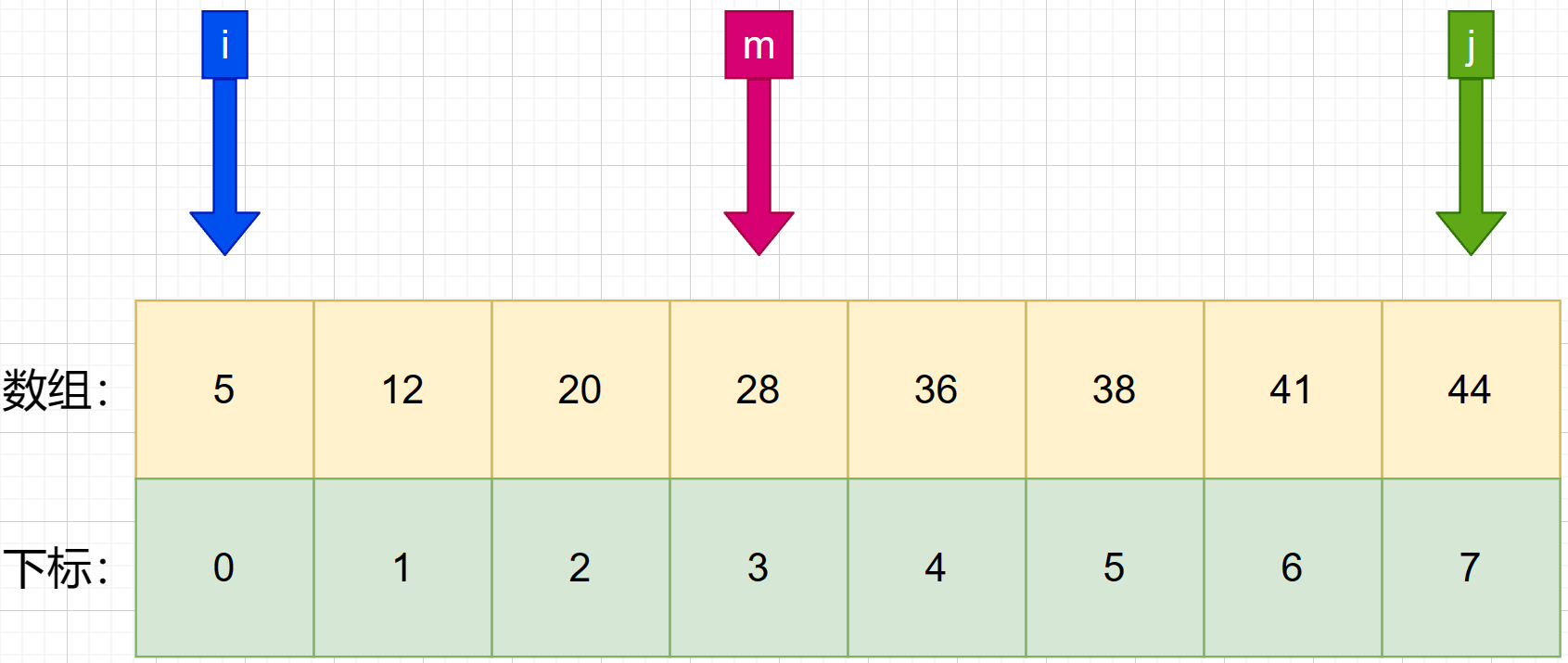
4、**判断第一次中间索引与待查值的大小。**发现 m 所对应的数为 28,大于待查值 26.就将 j 设置成 m-1 .
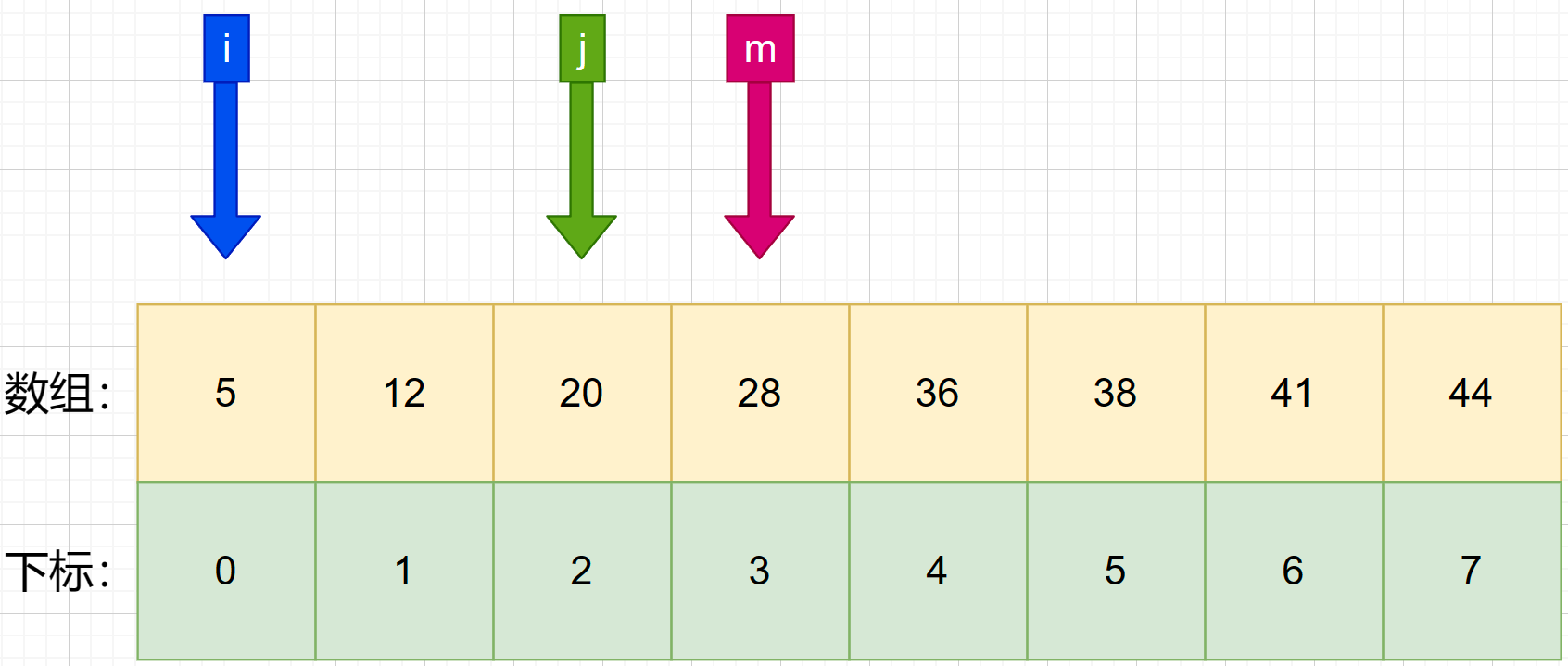
5、接着找第二次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(0+2)/ 2 = 1 .
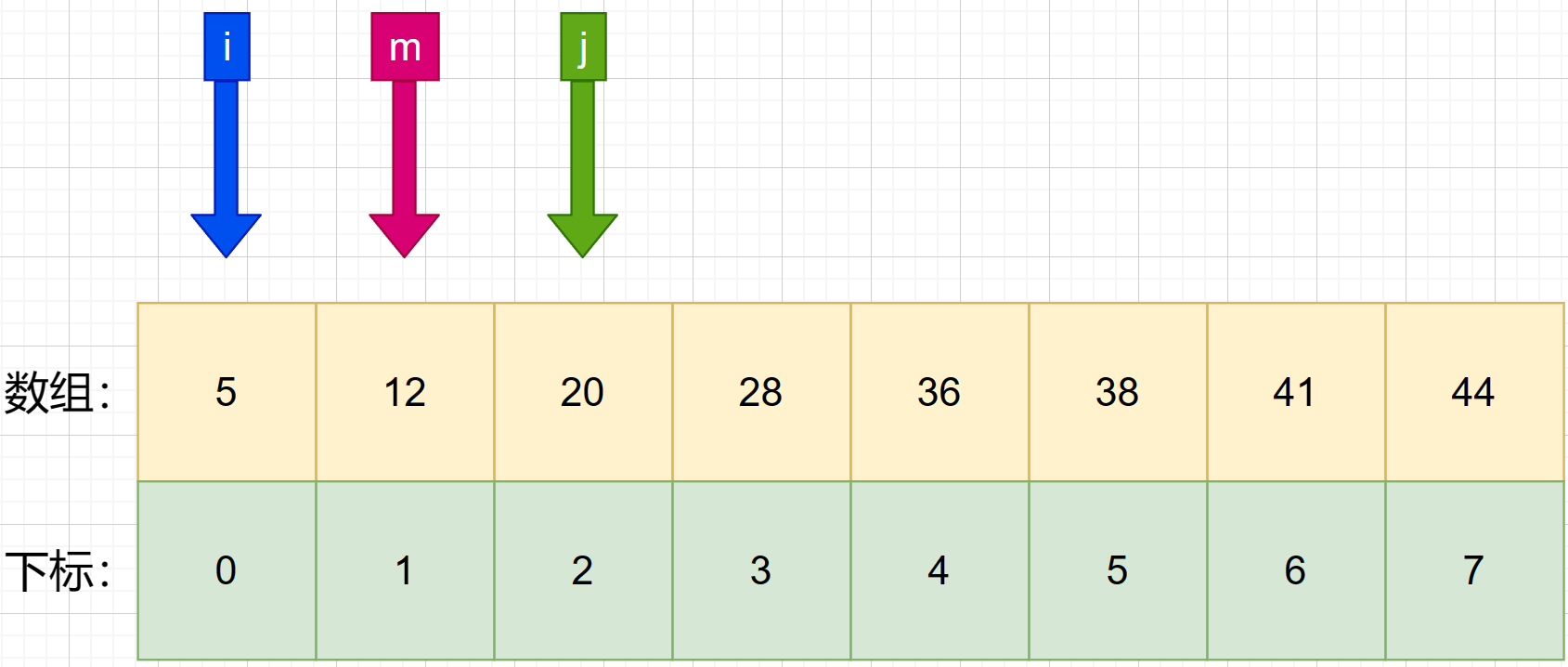
6、**判断第二次中间索引与待查值的大小。**发现 m 所对应的数为 12,小于待查值 36.就将 i 设置成 m+1 .
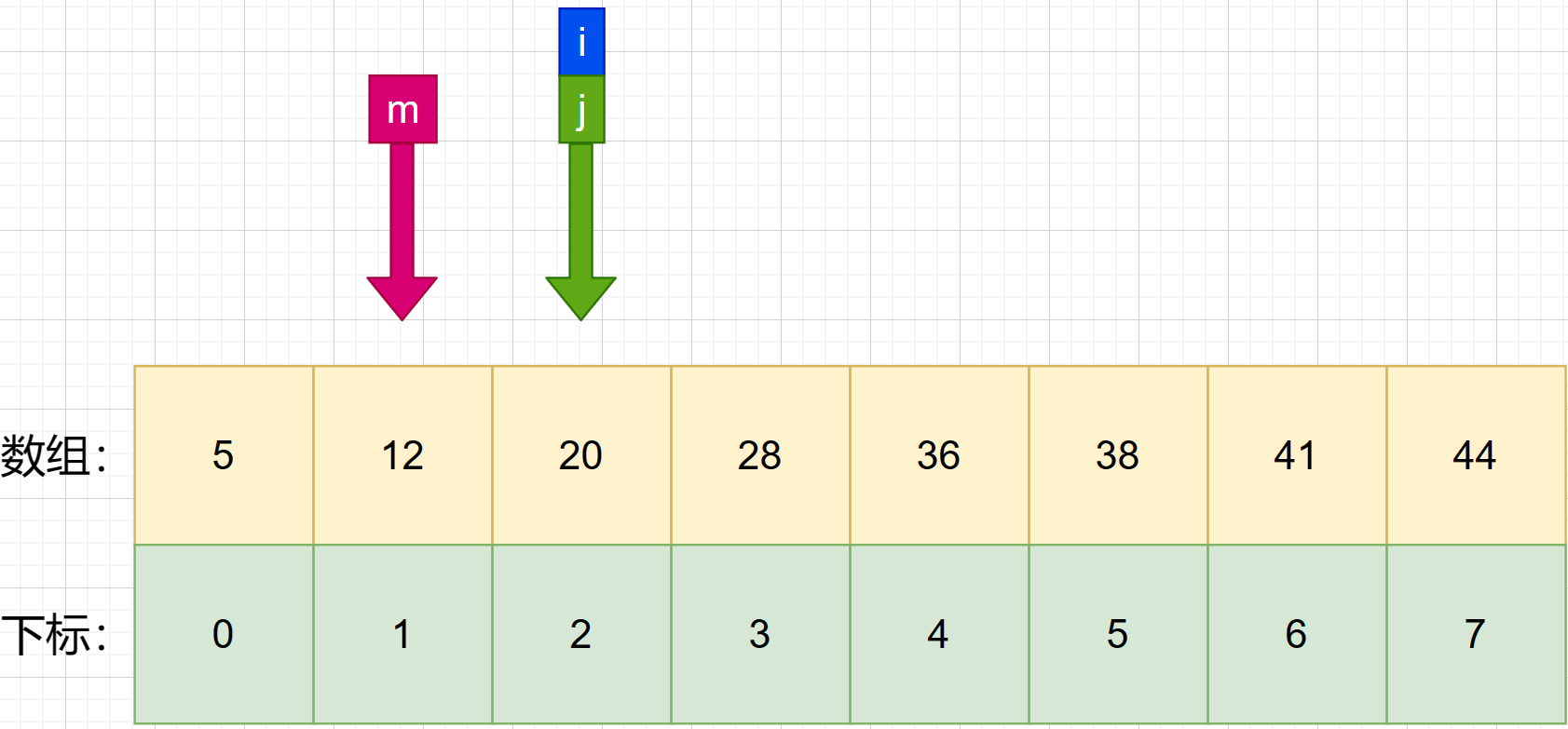
7、接着找第三次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(2+2)/ 2 = 2 .
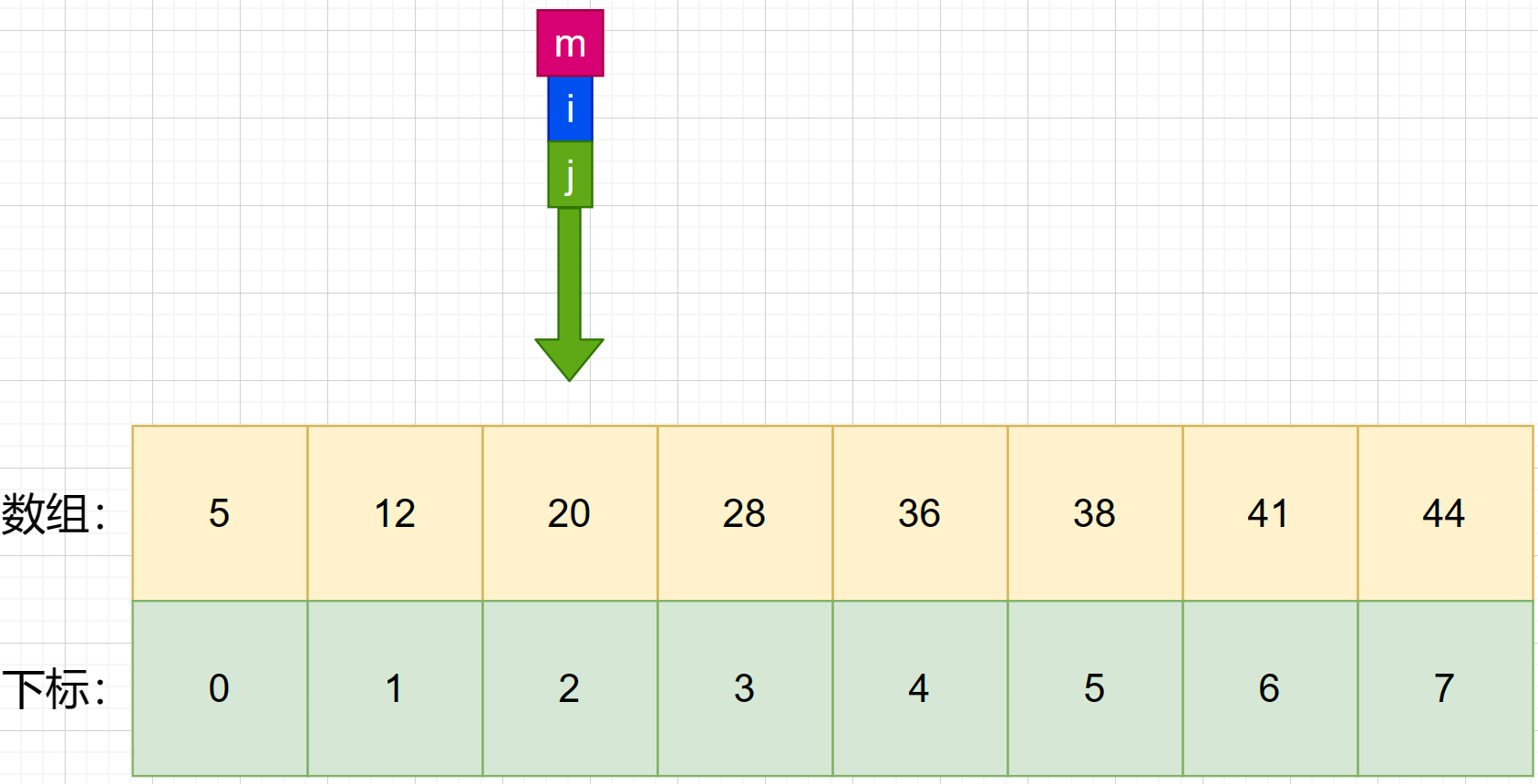
8、**判断第三次中间索引与待查值的大小。**发现 m 所对应的数为 20,小于待查值 36.我们再次将 i 设置成 m+1 .
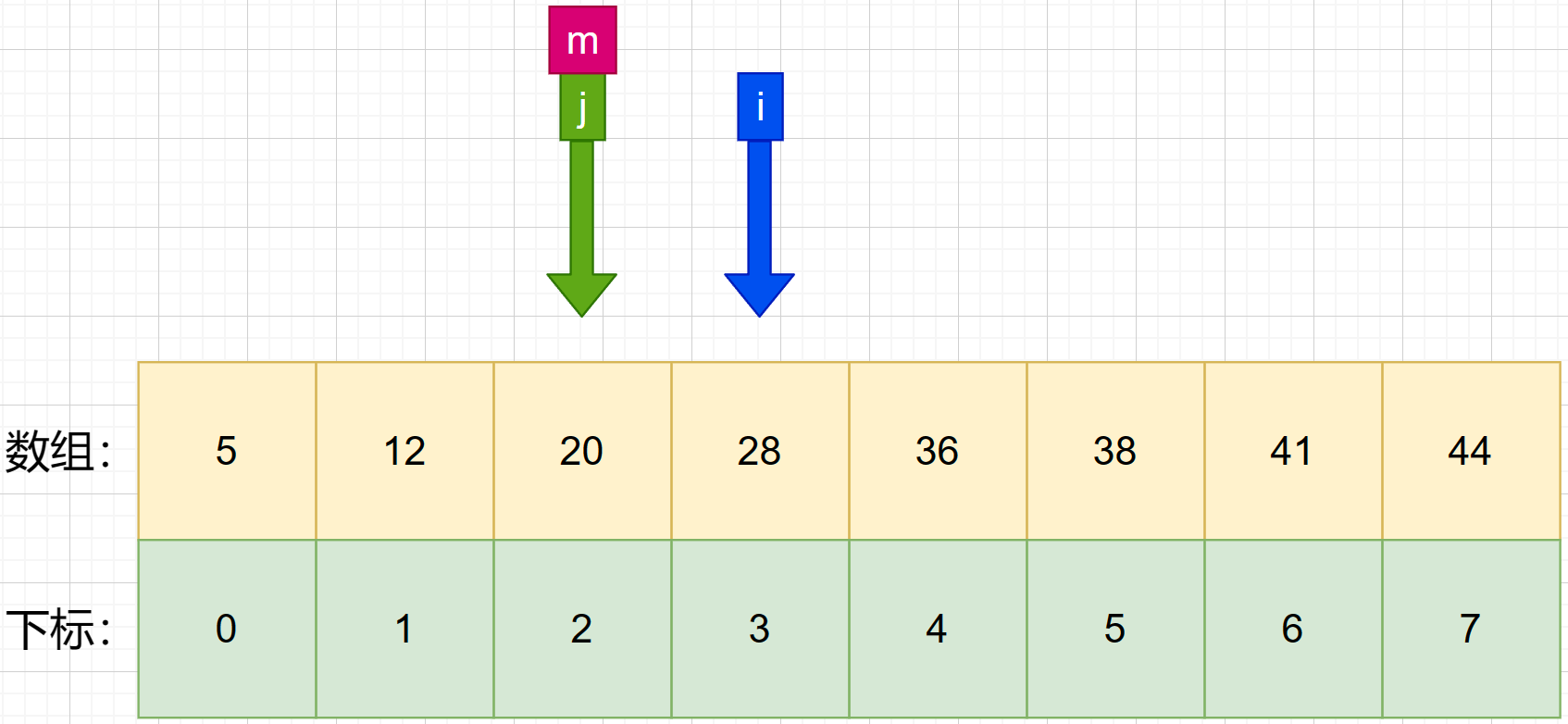
9、到这里我们能发现 i 已经大于 j ,能够证明我们找不到了,到此结束查找.
P.S.
- 对于一个算法来讲,都有较为严谨的描述,上面是一个例子
- 后续讲解时,以简明直白为目标,不会总以上面的方式来描述算法
翻译成代码
以:情况一:能在有序数组找到待查值 进行演示
1、给定一个有序数组。
【这一步可以通过测试代码进行测试、输出,放到后面去详细解释】

2、设置一个i值和一个j值,i从左边开始检索,j从右边开始检索。

这句话可以翻译成以下代码:
int i = 0;
int j = a.length - 1;
3、设定一个可以在数组中能找到的待查值target。接着开始二分查找。首先找中间索引 m ,使用公式
m
=
f
l
o
o
r
(
i
+
j
2
)
m = floor(\frac {i+j}{2})
m=floor(2i+j) 。在java中, int m = (i+j) / 2 ; 会自动地向下取整。

这句话可以翻译成以下代码:
while(i <= j) //只有在i <= j中,才可以通过二分查找找到数值
{
int m = (i+j) / 2 ;
}
return -1; //当i > j中,就证明无法找到了
4、**判断中间索引与待查值的大小。**发现 m 小于待查值就将 **i 设置成 m+1 .**若发现 m 大于待查值 36.就将 j 设置成 m-1 .如果发现 m 等于待查值就证明找到了,直接返回m值即可。

这句话可以翻译成以下代码:
if(a[m] > target) //目标待查值在m的左边
{
j = m - 1;
}
else if (a[m] < target)//目标待查值在m的右边
{
i = m + 1;
}
else //目标待查值等于m,证明找到了
{
return m;
}
基础版代码(包括测试类)
本代码仍然可以正常运行,不过如果想有更好更优化的代码可以向下继续观看。
public class 二分查找 {
public static int binarySearch(int[] a, int target) {
int i = 0;
int j = a.length - 1;
while(i <= j) //只有在i <= j中,才可以通过二分查找找到数值
{
int m = (i+j) / 2 ; //这里有点小问题,但不影响代码运行,具体可以跳到《疑惑解答》去了解
if(a[m] > target) //目标待查值在m的左边
{
j = m - 1;
}
else if (a[m] < target)//目标待查值在m的右边
{
i = m + 1;
}
else //目标待查值等于m,证明找到了
{
return m;
}
}
return -1; //当i > j中,就证明无法找到了
}
}
同时你也可以自己写一个junit测试类,来测试这段代码是否能正常运行:
package SuanFa.test;
import org.junit.jupiter.api.DisplayName;
import SuanFa.第一章_初始算法.数组.二分查找;
import static org.junit.jupiter.api.Assertions.*;
class 二分查找Test {
@org.junit.jupiter.api.Test
@DisplayName("binarySearch 找到!")
void testbinarySearch() {
int[] a = {7, 13, 24, 45, 66, 82, 94};
assertEquals(0,二分查找.binarySearch(a, 7));
}
}
然后发现测试是正常可运行的,证明我们代码暂时没有出现问题。
疑惑解答
问:那为什么是i<=j 意味着区间内有未比较的元素,而不是 i<j ?
答:因为 i , j 它们指向的元素也会参与比较
问:使用 (i+j) / 2 会不会出现问题呢?
答:第一段代码中,计算m的方式是(i+j) / 2,这是整数除法,会直接舍去小数部分。这种方式在m恰好是两个整数的中间值时可能会导致问题,因为如果i和j都是奇数,那么m就会偏向于左边,导致可能无法找到目标值。
所以我们可以进行一个改良,把计算m的方式改成(i + j) >>> 1,这是无符号右移操作,可以保证无论i和j的值如何,m都会取到它们中间位置的整数。这种方式可以避免上述问题。
基础版改良后代码
public static int binarySearch(int[] a, int target) {
int i = 0, j = a.length - 1;
while (i <= j) {
int m = (i + j) >>> 1; // 可以避免m找不到中间值的问题
if (target < a[m]) { // 在左边
j = m - 1;
} else if (a[m] < target) { // 在右边
i = m + 1;
} else {
return m;
}
}
return -1;
}
进阶版
进阶版相对于基础版,会进行三个地方的改动:
改动地方
改动一:i 跟 j 的边界位置
不希望j指的区域参与比较运算
int i = 0;
int j = a.length;
改动二:while 的条件
while(i < j)
{
……
}
改动三:if 判断中的 j 的边界问题
if(a[m] > target)
{
j = m;
}
改动后代码
package SuanFa.第一章_初始算法.数组;
public class 二分查找 {
public static int binarySearch(int[] a, int target) {
int i = 0;
int j = a.length;
while(i < j)
{
int m = (i+j) >>> 1 ;
if(a[m] > target)
{
j = m;
}
else if (a[m] < target)
{
i = m + 1;
}
else
{
return m;
}
}
return -1;
}
}
分步演示
1、给定一个有序数组,并且在其下面标上下标。并设置一个i值和一个j值,i从数组第0个元素开始向左检索,j从外界区域开始向右检索。
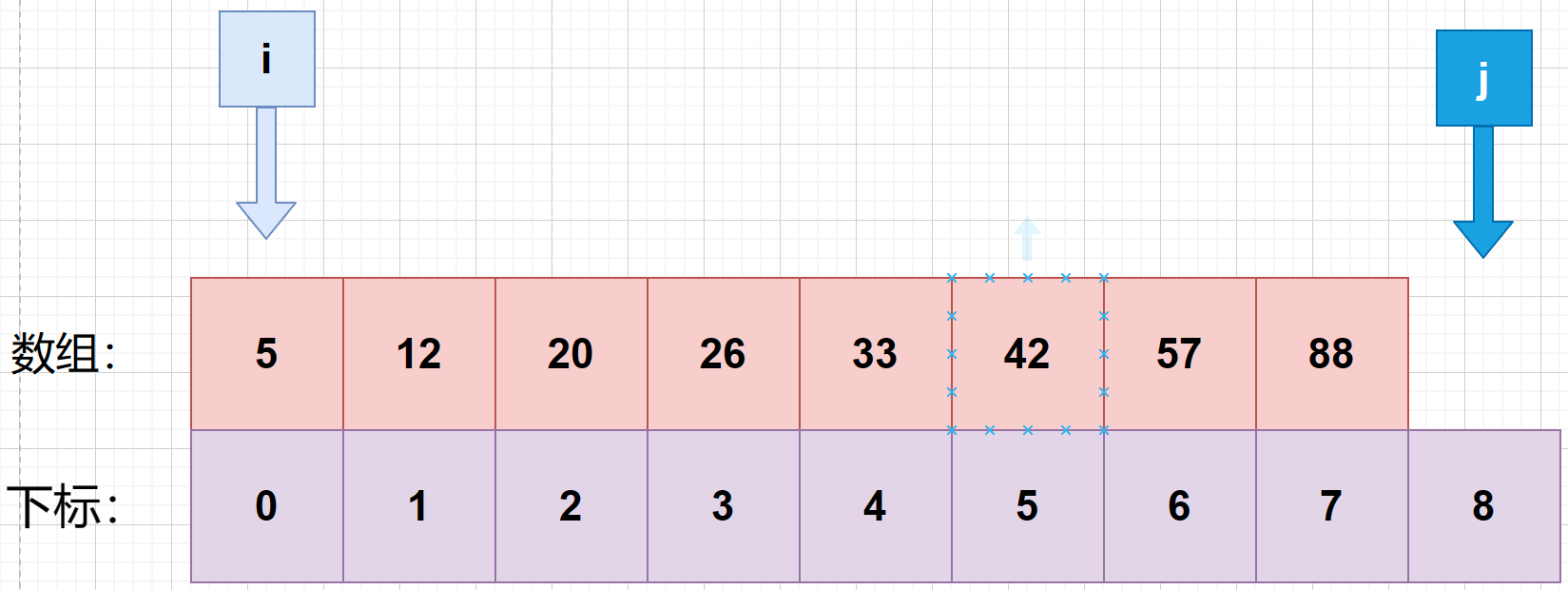
2、设定一个可以在数组中能找到的数值:26 作为待查值target。接着开始二分查找。首先找第一次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(0+8)>>> 1 = 4
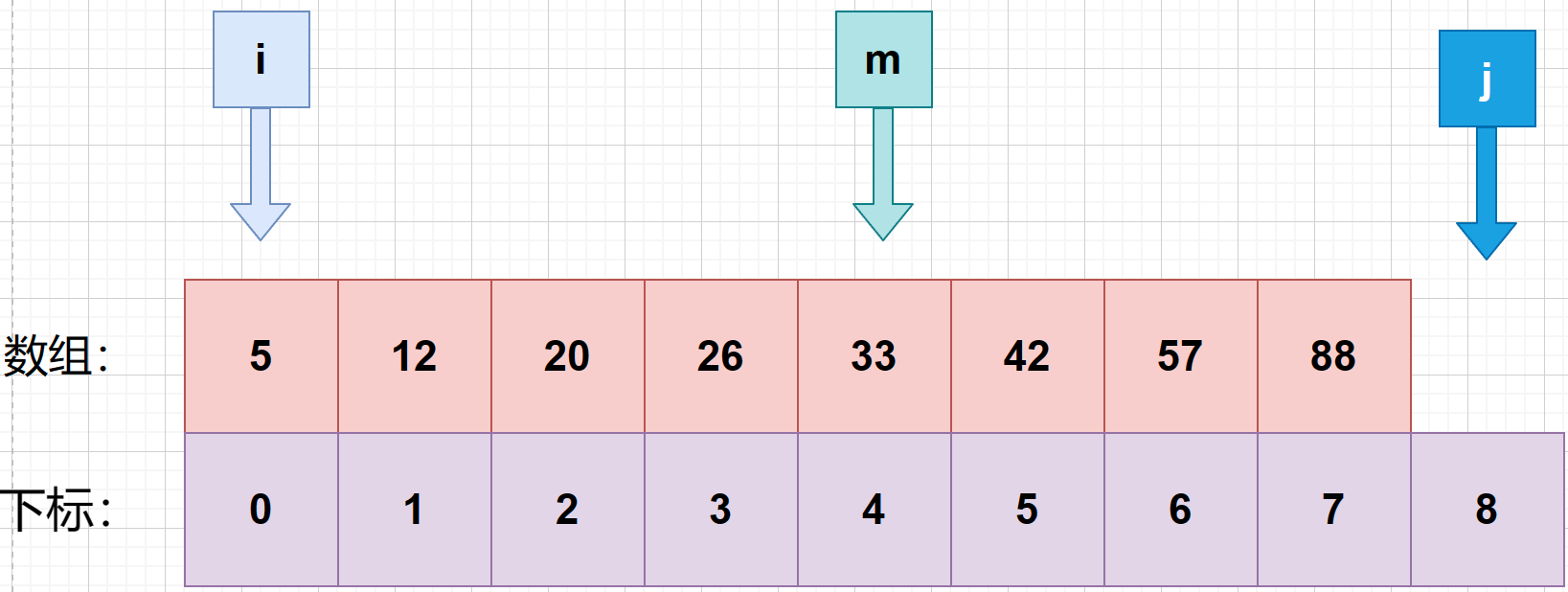
3、**判断第一次中间索引与待查值的大小。**发现 m 所对应的数为 33,大于待查值 26.就将 j 设置成 m .
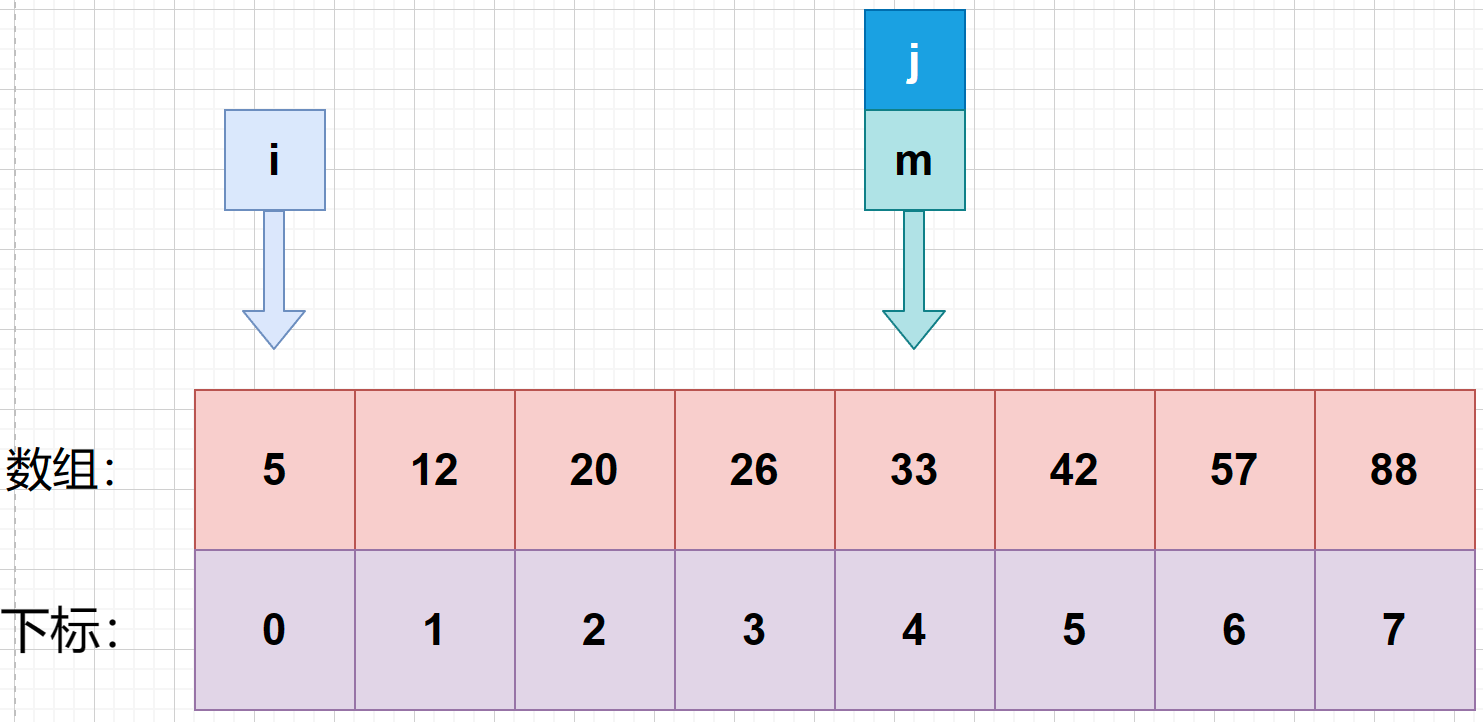
4、接着找第二次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(0+4)>>> 1= 2.
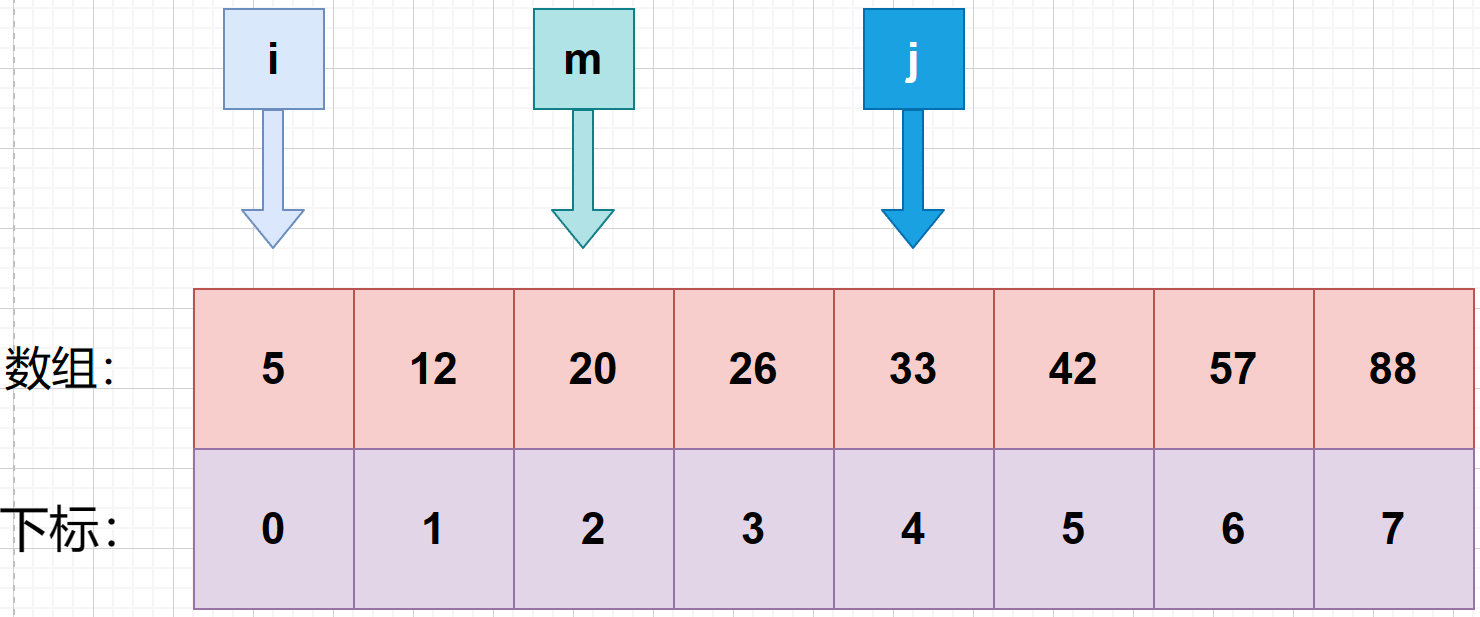
5、**判断第二次中间索引与待查值的大小。**发现 m 所对应的数为 20,小于待查值 26.就将 i 设置成 m+1 .
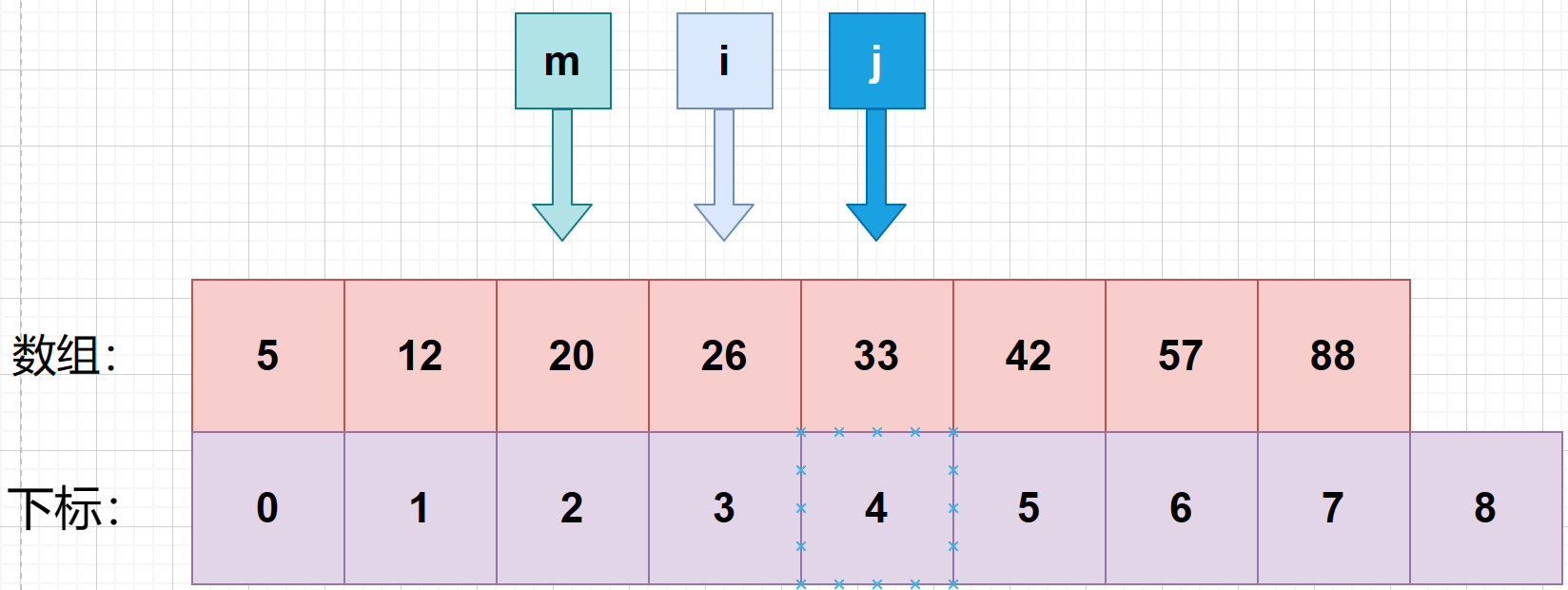
6、接着找第三次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(3+4)>>> 1 = 3 .(向下求值)
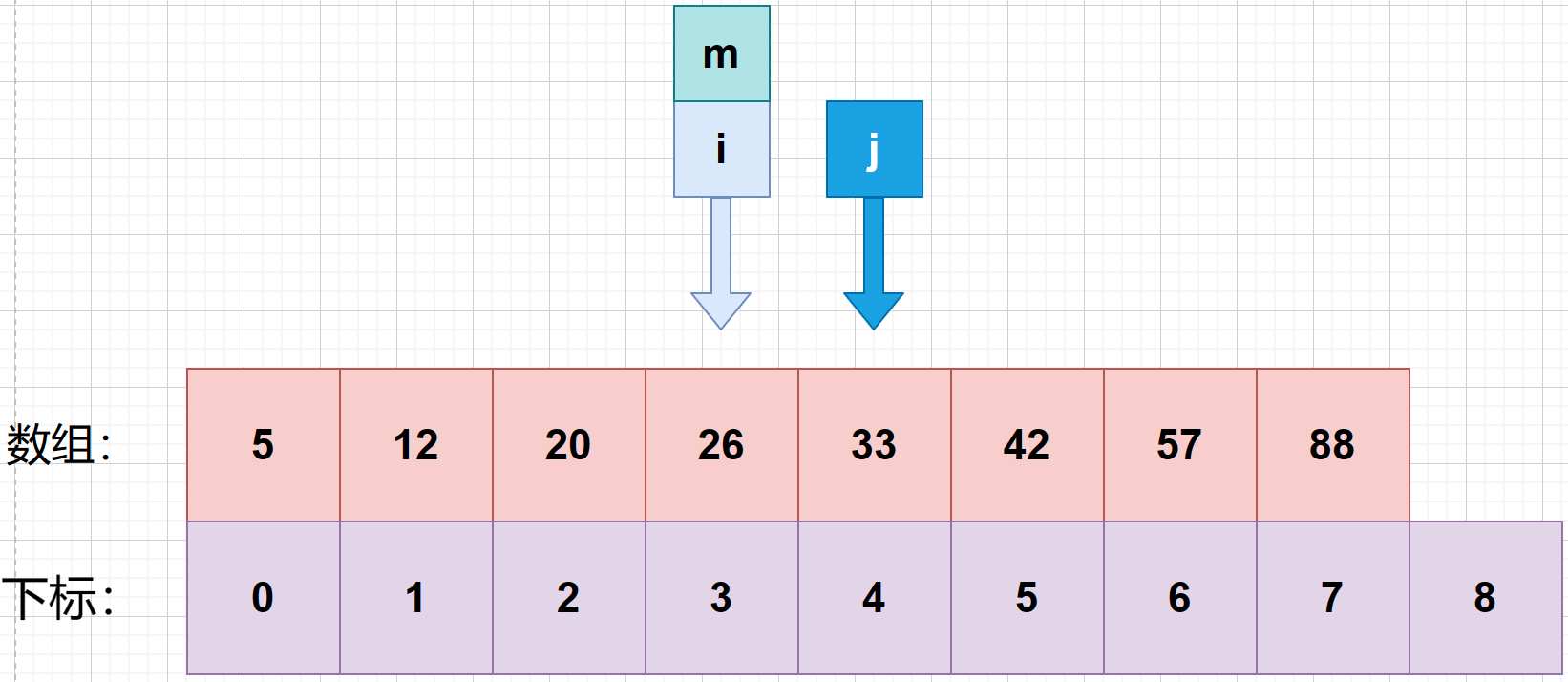
7、**判断第三次中间索引与待查值的大小。**发现 m 所对应的数为 26,等于待查值 26.到这里我们就通过二分查找找到了待查值。
改动地方的解释
i 跟 j 的边界位置改动原因
改动原因:不希望 j 指的区域参与比较运算,j 只需要作为 a.length ,下标为8 的元素即可
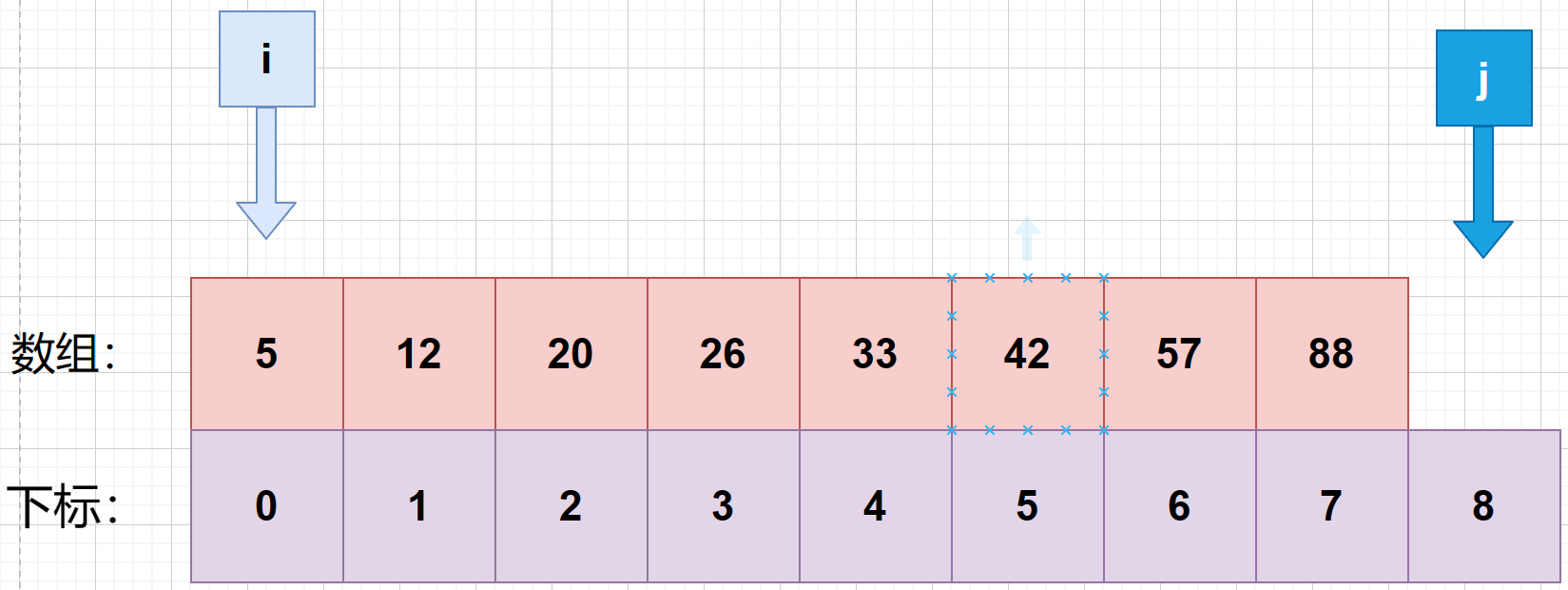
while 的条件改动原因
改动原因:i 的区域是要参与比较运算的,而 j 不需要。如果出现等于号,就有可能出现 i 带着 j 一起进行运算了。
注:当仅修改了 j = a.length 的条件,却没有改动 while 中 i <= j ,在查找数组中不存在的元素的话,就会发生死循环!
示例:
1、给定一个有序数组,并且在其下面标上下标。并设置一个i值和一个j值,i从数组第0个元素开始向左检索,j从外界区域开始向右检索。

2、设定一个可以在数组中找不到的数值:27 作为待查值target。接着开始二分查找。首先找第一次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(0+8)>>> 1 = 4

3、**判断第一次中间索引与待查值的大小。**发现 m 所对应的数为 33,大于待查值 27.就将 j 设置成 m .

4、接着找第二次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(0+4)>>> 1= 2.

5、**判断第二次中间索引与待查值的大小。**发现 m 所对应的数为 20,小于待查值 27.就将 i 设置成 m+1 .

6、接着找第三次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(3+4)>>> 1 = 3 .(向下求值)

7、**判断第三次中间索引与待查值的大小。**发现 m 所对应的数为 26,小于待查值 27.再将 i 设置成 m+1 .
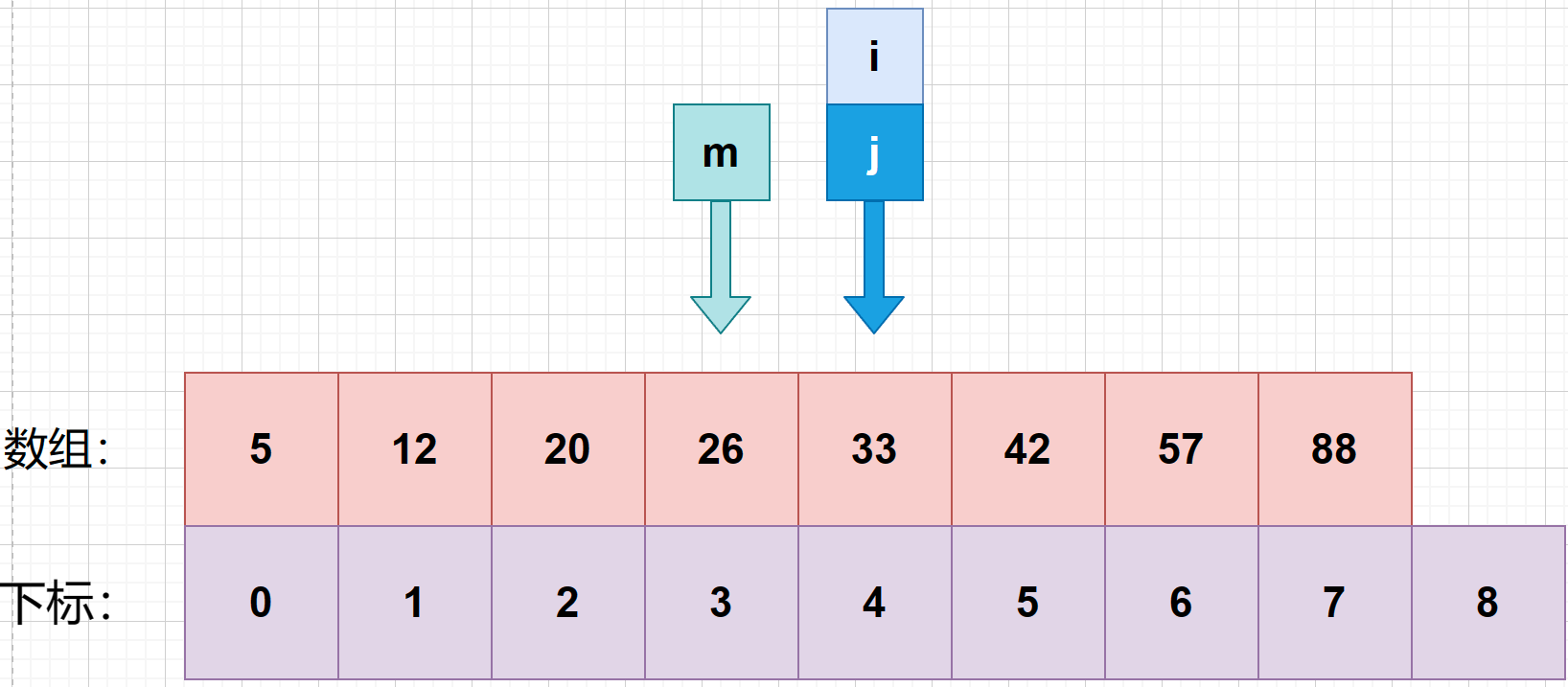
8、接着找第四次的中间索引 m ,使用公式 m = f l o o r ( i + j 2 ) m = floor(\frac {i+j}{2}) m=floor(2i+j) 可知:m=(4+4)>>> 1 = 4 .
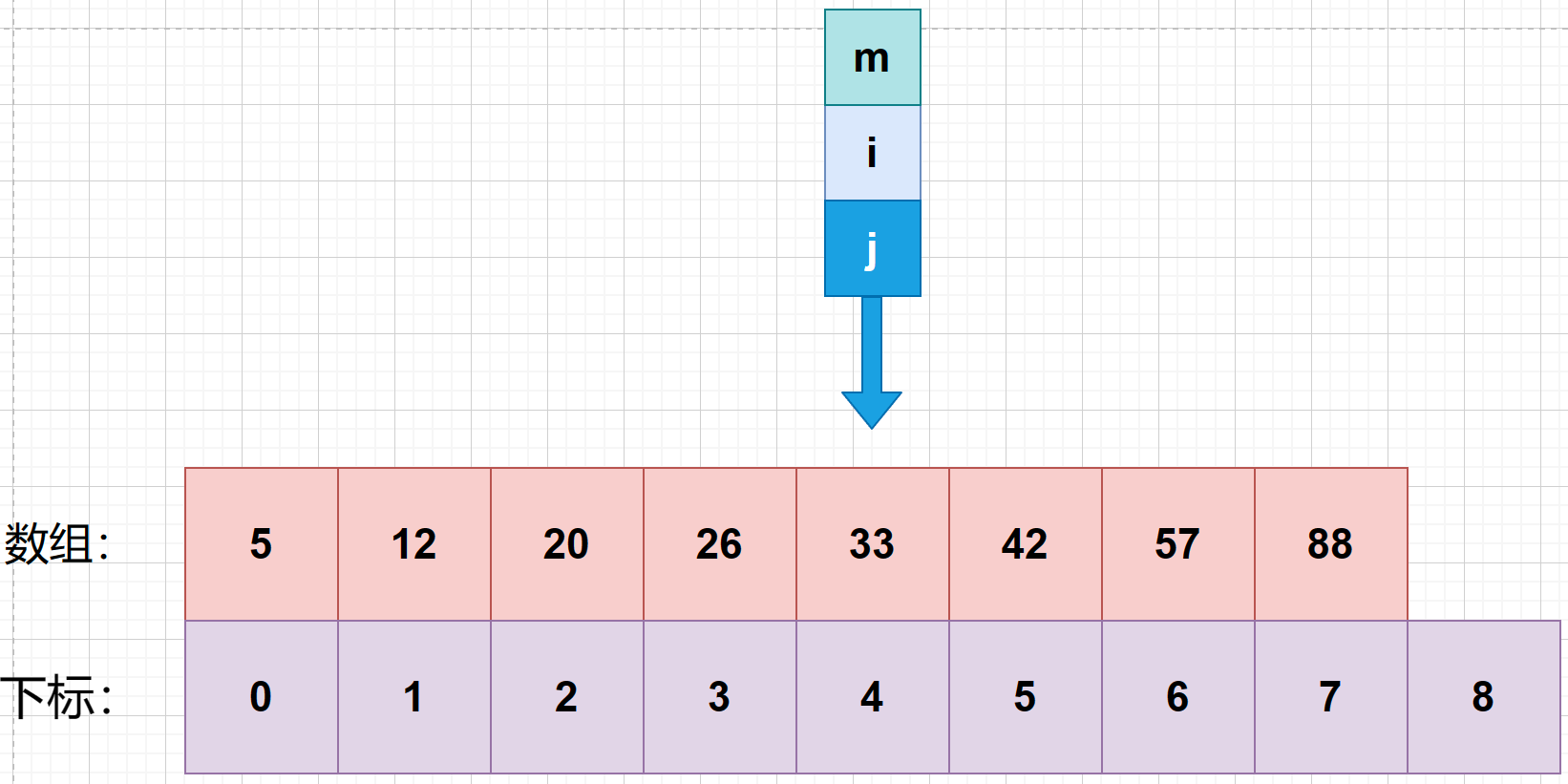
9、**判断第四次中间索引与待查值的大小。**发现 m 所对应的数为 33,大于待查值 27.再将 **j 设置成 m .**但由于原本的 j 就在下标为4的位置,此时就开始陷入死循环里了。
if 判断中的 j 的边界问题改动原因
改动三就很简单了,这里就不多赘述了。
衡量算法好坏
时间复杂度
下面的查找算法也能得出与之前二分查找一样的结果,那你能说出它差在哪里吗?
public static int search(int[] a, int k) {
for (
int i = 0;
i < a.length;
i++
) {
if (a[i] == k) {
return i;
}
}
return -1;
}
考虑最坏情况下(没找到)例如 [1,2,3,4] 查找 5
int i = 0只执行一次i < a.length受数组元素个数 n n n 的影响,比较 n + 1 n+1 n+1 次i++受数组元素个数 n n n 的影响,自增 n n n 次a[i] == k受元素个数 n n n 的影响,比较 n n n 次return -1,执行一次
粗略认为每行代码执行时间是 t t t,假设 n = 4 n=4 n=4 那么
- 总执行时间是 ( 1 + 4 + 1 + 4 + 4 + 1 ) ∗ t = 15 t (1+4+1+4+4+1)*t = 15t (1+4+1+4+4+1)∗t=15t
- 可以推导出更一般地公式为, T = ( 3 ∗ n + 3 ) t T = (3*n+3)t T=(3∗n+3)t
如果套用二分查找算法,还是 [1,2,3,4] 查找 5
public static int binarySearch(int[] a, int target) {
int i = 0, j = a.length - 1;
while (i <= j) {
int m = (i + j) >>> 1;
if (target < a[m]) { // 在左边
j = m - 1;
} else if (a[m] < target) { // 在右边
i = m + 1;
} else {
return m;
}
}
return -1;
}
-
int i = 0, j = a.length - 1各执行 1 次 -
i <= j比较 f l o o r ( log 2 ( n ) + 1 ) floor(\log_{2}(n)+1) floor(log2(n)+1) 再加 1 次 -
(i + j) >>> 1计算 f l o o r ( log 2 ( n ) + 1 ) floor(\log_{2}(n)+1) floor(log2(n)+1) 次 -
接下来
if() else if() else会执行 3 ∗ f l o o r ( log 2 ( n ) + 1 ) 3* floor(\log_{2}(n)+1) 3∗floor(log2(n)+1) 次,分别为- if 比较
- else if 比较
- else if 比较成立后的赋值语句
-
return -1,执行一次
结果:
- 总执行时间为 ( 2 + ( 1 + 3 ) + 3 + 3 ∗ 3 + 1 ) ∗ t = 19 t (2 + (1+3) + 3 + 3 * 3 +1)*t = 19t (2+(1+3)+3+3∗3+1)∗t=19t
- 更一般地公式为 ( 4 + 5 ∗ f l o o r ( log 2 ( n ) + 1 ) ) ∗ t (4 + 5 * floor(\log_{2}(n)+1))*t (4+5∗floor(log2(n)+1))∗t
注意:
左侧未找到和右侧未找到结果不一样,这里不做分析
两个算法比较,可以看到 n n n 在较小的时候,二者花费的次数差不多

但随着 n n n 越来越大,比如说 n = 1000 n=1000 n=1000 时,用二分查找算法(红色)也就是 54 t 54t 54t,而蓝色算法则需要 3003 t 3003t 3003t
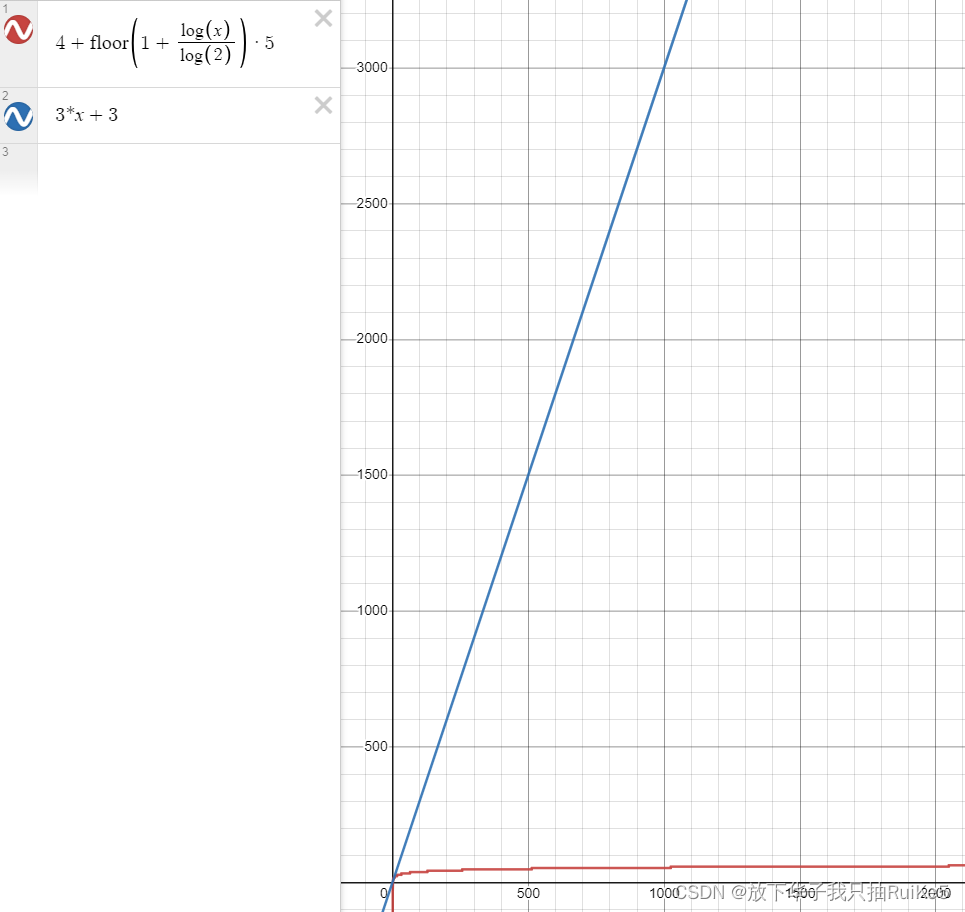
计算机科学中,时间复杂度是用来衡量:一个算法的执行,随数据规模增大,而增长的时间成本
- 不依赖于环境因素
如何表示时间复杂度
-
假设算法要处理的数据规模是 n n n,代码总的执行行数用函数 f ( n ) f(n) f(n) 来表示,例如:
- 线性查找算法的函数 f ( n ) = 3 ∗ n + 3 f(n) = 3*n + 3 f(n)=3∗n+3
- 二分查找算法的函数 f ( n ) = ( f l o o r ( l o g 2 ( n ) ) + 1 ) ∗ 5 + 4 f(n) = (floor(log_2(n)) + 1) * 5 + 4 f(n)=(floor(log2(n))+1)∗5+4
-
为了对 f ( n ) f(n) f(n) 进行化简,应当抓住主要矛盾,找到一个变化趋势与之相近的表示法
大 O O O 表示法
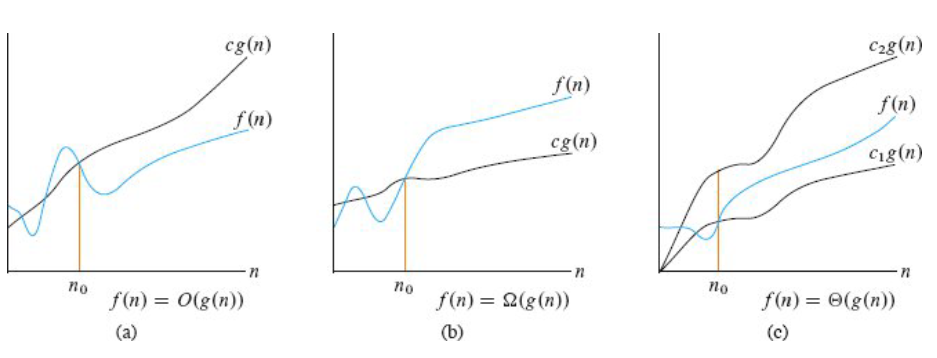
其中
- c , c 1 , c 2 c, c_1, c_2 c,c1,c2 都为一个常数
- f ( n ) f(n) f(n) 是实际执行代码行数与 n 的函数
- g ( n ) g(n) g(n) 是经过化简,变化趋势与 f ( n ) f(n) f(n) 一致的 n 的函数
渐进上界
渐进上界(asymptotic upper bound):从某个常数 n 0 n_0 n0开始, c ∗ g ( n ) c*g(n) c∗g(n) 总是位于 f ( n ) f(n) f(n) 上方,那么记作 O ( g ( n ) ) O(g(n)) O(g(n))
- 代表算法执行的最差情况
例1:
- f ( n ) = 3 ∗ n + 3 f(n) = 3*n+3 f(n)=3∗n+3
- g ( n ) = n g(n) = n g(n)=n
- 取 c = 4 c=4 c=4,在 n 0 = 3 n_0=3 n0=3 之后, g ( n ) g(n) g(n) 可以作为 f ( n ) f(n) f(n) 的渐进上界,因此表示法写作 O ( n ) O(n) O(n)
例2:
- f ( n ) = 5 ∗ f l o o r ( l o g 2 ( n ) ) + 9 f(n) = 5*floor(log_2(n)) + 9 f(n)=5∗floor(log2(n))+9
- g ( n ) = l o g 2 ( n ) g(n) = log_2(n) g(n)=log2(n)
- O ( l o g 2 ( n ) ) O(log_2(n)) O(log2(n))
已知 f ( n ) f(n) f(n) 来说,求 g ( n ) g(n) g(n)
- 表达式中相乘的常量,可以省略,如
- f ( n ) = 100 ∗ n 2 f(n) = 100*n^2 f(n)=100∗n2 中的 100 100 100
- 多项式中数量规模更小(低次项)的表达式,如
- f ( n ) = n 2 + n f(n)=n^2+n f(n)=n2+n 中的 n n n
- f ( n ) = n 3 + n 2 f(n) = n^3 + n^2 f(n)=n3+n2 中的 n 2 n^2 n2
- 不同底数的对数,渐进上界可以用一个对数函数
log
n
\log n
logn 表示
- 例如: l o g 2 ( n ) log_2(n) log2(n) 可以替换为 l o g 10 ( n ) log_{10}(n) log10(n),因为 l o g 2 ( n ) = l o g 10 ( n ) l o g 10 ( 2 ) log_2(n) = \frac{log_{10}(n)}{log_{10}(2)} log2(n)=log10(2)log10(n),相乘的常量 1 l o g 10 ( 2 ) \frac{1}{log_{10}(2)} log10(2)1 可以省略
- 类似的,对数的常数次幂可省略
- 如: l o g ( n c ) = c ∗ l o g ( n ) log(n^c) = c * log(n) log(nc)=c∗log(n)
常见大 O O O 表示法
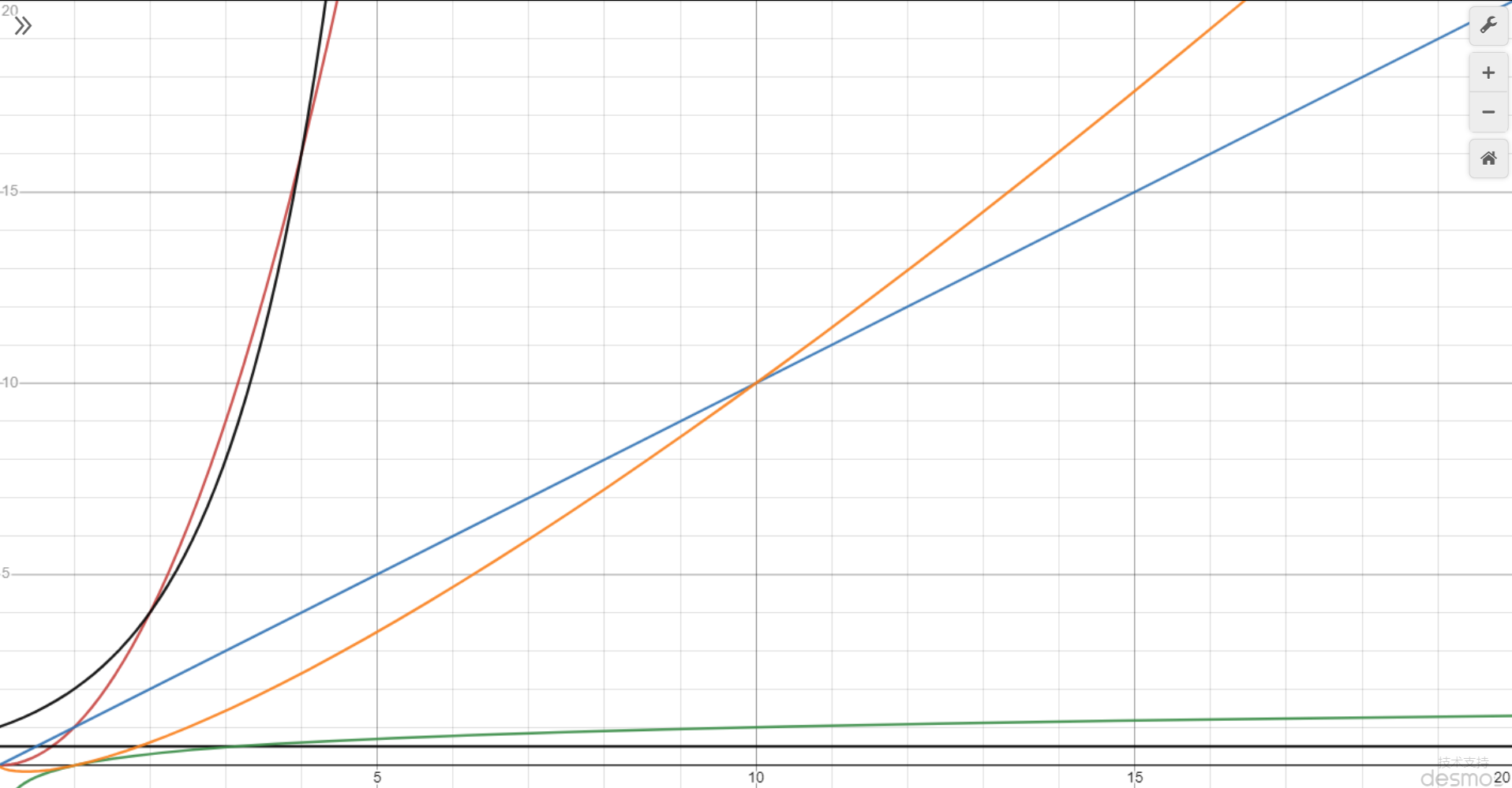
按时间复杂度从低到高
- 黑色横线 O ( 1 ) O(1) O(1),常量时间,意味着算法时间并不随数据规模而变化
- 绿色 O ( l o g ( n ) ) O(log(n)) O(log(n)),对数时间
- 蓝色 O ( n ) O(n) O(n),线性时间,算法时间与数据规模成正比
- 橙色 O ( n ∗ l o g ( n ) ) O(n*log(n)) O(n∗log(n)),拟线性时间
- 红色 O ( n 2 ) O(n^2) O(n2) 平方时间
- 黑色朝上 O ( 2 n ) O(2^n) O(2n) 指数时间
- 没画出来的 O ( n ! ) O(n!) O(n!) ☞ 指n的阶乘,是时间复杂度最大的
渐进下界
渐进下界(asymptotic lower bound):从某个常数 n 0 n_0 n0开始, c ∗ g ( n ) c*g(n) c∗g(n) 总是位于 f ( n ) f(n) f(n) 下方,那么记作 Ω ( g ( n ) ) \Omega(g(n)) Ω(g(n))
渐进紧界
渐进紧界(asymptotic tight bounds):从某个常数 n 0 n_0 n0开始, f ( n ) f(n) f(n) 总是在 c 1 ∗ g ( n ) c_1*g(n) c1∗g(n) 和 c 2 ∗ g ( n ) c_2*g(n) c2∗g(n) 之间,那么记作 Θ ( g ( n ) ) \Theta(g(n)) Θ(g(n))
空间复杂度
与时间复杂度类似,一般也使用大 O O O 表示法来衡量:一个算法执行随数据规模增大,而增长的额外空间成本*(额外指的是原始数据所占的空间不用算)
public static int binarySearchBasic(int[] a, int target) {
int i = 0, j = a.length - 1; // 设置指针和初值
while (i <= j) { // i~j 范围内有东西
int m = (i + j) >>> 1;
if(target < a[m]) { // 目标在左边
j = m - 1;
} else if (a[m] < target) { // 目标在右边
i = m + 1;
} else { // 找到了
return m;
}
}
return -1;
}
二分查找性能
下面分析二分查找算法的性能
时间复杂度
- 最坏情况: O ( log n ) O(\log n) O(logn)
- 最好情况:如果待查找元素恰好在数组中央,只需要循环一次 O ( 1 ) O(1) O(1)
空间复杂度
- 需要常数个指针 i , j , m i,j,m i,j,m,因此额外占用的空间是 O ( 1 ) O(1) O(1)
平衡版
与前面的基础版与进阶版不同的是:只用 if-else 即可
public static int binarySearchBalance(int[] a, int target) {
int i = 0, j = a.length;
while (1 < j - i) {
int m = (i + j) >>> 1;
if (target < a[m]) {
j = m;
} else {
i = m;
}
}
return (a[i] == target) ? i : -1;
}
思想:
- 左闭右开的区间, i i i 指向的可能是目标,而 j j j 指向的不是目标
- 不奢望循环内通过
m
m
m 找出目标, 缩小区间直至剩 1 个, 剩下的这个可能就是要找的(通过
i
i
i)
- j − i > 1 j - i > 1 j−i>1 的含义是,在范围内待比较的元素个数 > 1
- 改变 i i i 边界时,它指向的可能是目标,因此不能 m + 1 m+1 m+1
- 循环内的平均比较次数减少了
- 时间复杂度 Θ ( l o g ( n ) ) \Theta(log(n)) Θ(log(n))
算法题实战:力扣704 . 二分查找
具体的解题过程可以跳转到我的另一篇博客进行观看:代码随想录—力扣算法题:704二分查找.Java版(示例代码与导图详解)