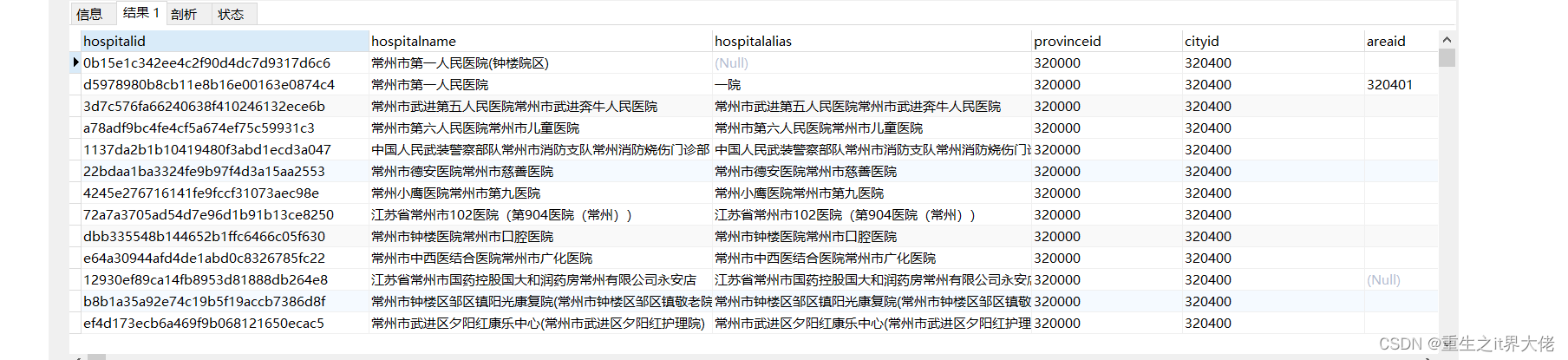
信息论

香农信息论发表于1948/1949年，它由三部分组成：信号采样、信源编码、信道编码；

• 信号采样：采样理论研究在何种条件下对连续信号进行采样，从而得到的离散型号可以可逆地恢复出采样前的连续信号。采样得到的离散实数值代表着原来的信号，信号通常有限精度量化成一个有限的符号集中。

• 信源编码：信源编码研究如何将采样得到的离散数字信号编码成二进制序列，它利用了信号的统计分布来将采集到的数字信号编码成最紧凑的二进制码。

• 信道编码：信道编码研究如何给已经编码的序列中添加冗余性，从而使它对传输中引入的错误或者攻击（比如某些比特位存一定概率的翻转）更具有鲁邦性；它有时候也叫做纠错码理论。

信号采样

1.1 模拟信号与数字信号

为了能够利用数学工具分析性能，数学建模通常建立在连续信号（也称为模拟信号）上。连续信号的设定的目的是为了能够表示物理世界采集到的真实信号，比如从麦克风、数字相机或者医疗设备等传感器硬件采集的输入信号。模拟信号是一个一维函数$f_0\in L^2([0,1])$，其中$[0,1]$表示的信号采集域，比如通常可能是时间轴。图像的模拟信号是一个二维函数$f_0\in L^2([0,1{]}^2)$，其中单位正方形区域$[0,1{]}^2$是图像空间区域。
尽管目前仅仅关注在声音和自然图像信号的处理中，但是这些方法中绝大部分都可以延伸到多维信号数据集的处理上，多维信号具有更高的维度间的映射：

$$f_0:[0,1{]}^d\to [0,1{]}^2$$

其中$d$是输入空间的维度（$d=1$表示声音信号，$d=2$表示图像信号），$s$表示特征空间的维度。比如，对于灰度图像$d=2,s=1$，对于视频图像$d=3,s=1$，对于彩色图像$d=2,s=3$因为彩色图像有R/G/B三个通道。对于多光谱图像$d=2,s\gg 3$因为它由大量的不同波段信号的采样。图1.1和图1.2是这样信号的一些基本例子。

1.1.1 信号获取与采样

信号采集是一个通过硬件设备将连续信号采集成离散信号的低维投影映射。麦克风是一维信号采样的例子，数字相机是二维采样的例子，采样操作对应这将连续函数信号映射到N维向量N的过程，可以用如下公式表示：
$$f_0\in L^2([0,1{]}^d)\to f\in {\mathbb{C}}^N$$

图1.3是一些离散信号的例子

1.1.2 线性移不变采样器

线性移不变采样器执行采样操作是将连续信号和一个不变的脉冲响应$h$在采样位置进行卷积运算
$$f_n={\int }_{-S/2}^{S/2}{f}_0(x)h(n/N-x)dx=f_0\star h(n/N)\text{\hspace{1em}(1.1)}$$

函数$h(x)$的精确形状取决于采样设备，它通常是一个低通滤波器，并且在0附近取得最大值。采样器的尺寸$S$决定了采样设备的采样精度，它通常是与$1/N$同数量级的，如果S太大，会模糊信号，如果S太小，则会产生混叠现象。

1.2 香农采样定理

傅里叶变换回顾：对于$f\in L^1(\mathbb{R})$，它的傅里叶变换定义为：
$$\forall \omega \in \mathbb{R},\hat{f}(\omega )={\int }_{\mathbb{R}}f(x)e^{-ix\omega }dx.\text{\hspace{1em}(1.2)}$$

由于有$||\hat{f}|{|}^2=(2\pi {)}^{-1}||f|{|}^2$，因此$f\to \hat{f}$可以扩展到连续的$L^2(\mathbb{R})$，这样计算函数$f$的傅里叶变换$\hat{f}$可以看做$li{m}_{T\to +\infty }{\int }_{-T}^{T}f(x)e^{-ix\omega }dx$。当$\hat{f}\in L^1(\mathbb{R})$，我们可以得到傅里叶逆变换：
$$f(x)=\frac{1}{2\pi }{\int }_{\mathbb{R}}\hat{f}(\omega )e^{ix\omega }d\omega ,\text{\hspace{1em}(1.3)}$$

这表示了函数$f$是连续的，并且在$\pm \infty$处极限趋于0。
傅里叶变换$\mathcal{F}:f\to \hat{f}$交换了函数的正则性和衰减性。例如，如果$f\in C^p(\mathbb{R})$，具有可积的傅里叶变换，那么$\mathcal{F}(f^{(p)})(\omega )=(i\omega {)}^p\hat{f}(\omega )$，因此$|\hat{f}(\omega )|=O(1/|\omega {|}^p)$。相反地，
$${\int }_{\mathbb{R}}(1+|\omega |{)}^p|\hat{f}(\omega )|d\omega <+\infty \Rightarrow f\in C^p(\mathbb{R})\text{\hspace{1em}(1.4)}$$

例如，当$\hat{f}(\omega )=O(1/|\omega {|}^{p+2})$，可以推出$f\in C^p(\mathbb{R})$。

傅里叶级数回顾：我们记$\mathbb{T}=\mathbb{R}/2\pi \mathbb{Z}$为一系列的$2\pi$为周期的区间列。函数$f\in L^2(\mathbb{T})$是一个以$2\pi$为周期的函数，它可以看成$f\in L^2([0,2\pi ])$，于是它的傅里叶系数为：
$$\forall n\in \mathbb{Z},\widehat{f_n}=\frac{1}{2\pi }{\int }_0^{2\pi }f(x)e^{-ixn}dx.$$

这个公式等价于求函数$f$与基函数$e_n$的内积$\widehat{f_n}=<f,e_n>$，内积定义为$<f,g>=\frac{1}{2\pi }{\int }_{\mathbb{T}}f(x)\overline{g}(x)dx$。在这里的内积中，$e_n$是希尔伯特空间中的正交基，这意味着，可以通过如下收敛级数进行重建
$$f=\sum _{n\in \mathbb{Z}}<f,e_n>e_n\text{\hspace{1em}(1.5)}$$

这意味着，在$N\to +\infty$时，$||f-{\sum }_{n=-N}^N<f,e_n>e_n|{|}_{L^2(\mathbb{T})}\to 0$。如果函数$f$可微，那么在$x\in \mathbb{T}$上可以保证公式（1.5）按点收敛。如果函数存在阶跃点，那么在这些点数存在Gibbs震荡，从而不能保证一致收敛，但是级数仍然收敛域该点的左极限和右极限的一半。

泊松公式：泊松公式连接了傅里叶变换与傅里叶技术到信号采样与周期化操作。对于某个定义在$\mathbb{R}$的函数$h(\omega )$，它的周期化为：
$$h_P(\omega )=\sum _{n}h(\omega -2\pi n)\text{\hspace{1em}(1.6)}$$

这个公式有意义的前提是$h\in L^1(\mathbb{R})$， 并且在这种情况下$||h_P|{|}_{L^1(\mathbb{T})}\le ||h|{|}_{L^1(\mathbb{R})}$。泊松公式阐明了如下关系：
（1）信号$f(x)$通过采样得到采样序列$(f(n){)}_n$，对采样采样序列的傅里叶级数为${\sum }_{n}f(n)e^{-i\omega n}$；
（2）信号$f(x)$做傅里叶变换得到$\hat{f}(\omega )$，对傅里叶此福利也变化进行周期化，得到傅里叶级数${\sum }_{n}f(n)e^{-i\omega n}$；

引理1 （泊松公式）：假设$\hat{f}$是紧支撑的，并且$|f(x)|\le C(1+|x|{)}^{-3}$，其中C为某个常数，于是有
$$\forall \omega \in \mathbb{R},\sum _{n}f(n)e^{-i\omega n}={\hat{f}}_P(\omega ).\text{\hspace{1em}(1.7)}$$

证明：由于$\hat{f}$是紧支撑的，${\hat{f}}_P$是良定义的，并且$f$很快衰减，由公式（1.4）可知$(\hat{f}{)}_P$是$C^1$。于是可以由傅里叶级数展开
$$(\hat{f}{)}_P(\omega )=\sum _k{c}_k{e}^{ik\omega }\text{\hspace{1em}(1.8)}$$

其中
$$c_k=\frac{1}{2\pi }{\int }_0^{2\pi }(\hat{f}{)}_P(\omega )e^{-ik\omega }d\omega =\frac{1}{2\pi }{\int }_0^{2\pi }\sum _n\hat{f}(\omega -2\pi n)e^{-ik\omega }d\omega$$

又有
$${\int }_0^{2\pi }\sum _n|\hat{f}(\omega -i\pi n)e^{-ik\omega }|d\omega ={\int }_{\mathbb{R}}|\hat{f}|$$

由于$\hat{f}\in L^1(\mathbb{R})$是有界的，因此可以交换求和符号与积分号的运算顺序
$$c_k=\sum _n\frac{1}{2\pi }{\int }_0^{2\pi }\hat{f}(\omega -2\pi n)e^{-ik\omega }d\omega =\frac{1}{2\pi }{\int }_{mathbbR}\hat{f}(\omega )e^{-ik\omega }d\omega =f(-k)$$

由于$\hat{f}\in L^1(\mathbb{R})$，因此这里我们运用（1.3）式中的傅里叶反变换是合理的。

注：这里我们进一步解释一下引理1的内容，信号$f(t)$的傅里叶变换为$\hat{f}(\omega )$，我们对信号$f(t)$在离散点$n$处进行采样得到离散信号$f(n)$，离散信号$f(n)$的福利变换为${\sum }_{n}f(n)e^{-i\omega n}$，而引理1则说明了离散采样信号$f(n)$的傅里叶变换等于原始连续信号$f(t)$的傅里叶变换按照以$2\pi$为周期进行周期化的结果。

香农采样定理：香农采样定理描述在什么采样步长$s>0$的采样操作$f\to (f(ns){)}_n$下信号可以可逆恢复出原始信号的充分条件。它需要采样信号的频谱满足$supp(\hat{f})\subset [-\pi /s,\pi /s]$。这个定理被奈奎斯特在1928年重新证明。它由于香农将其放于数字通信的论文中而变得非常出名。

定理1：如果对于某个常数C有$|f(x)|\le C(1+|x|{)}^{-3}$且$supp\hat{f}\subset [-\pi /s,\pi /s]$，于是有
$$\forall x\in \mathbb{R}f(x)=\sum _{n}f(ns)sinc(x/s-n)，其中sinc(u)=\frac{sin(\pi u)}{\pi u}\text{\hspace{1em}(1.9)}$$

一致收敛。
证明：令$g(x)=f(sx)$，那么$\hat{g}(\omega )=1/s\hat{f}(\omega /s)$，事实上，令$z=sx$，那么有
$$\hat{g}(\omega )=\int f(sx)e^{-i\omega x}dx=\frac{1}{s}\int f(z)e^{-i(\omega /s)z}dz=\hat{f}(\omega /s)/s,$$

为了研究方便，我们把$s$置为1。紧支撑假设含有$\hat{f}(\omega )=1_{[-pi,pi]}(\omega ){\hat{f}}_P(\omega )$。联合（1.3）式的逆变换与泊松公式（1.8），有
$$f(x)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }\hat{f}(\omega )e^{i\omega x}d\omega =\frac{1}{2\pi }{\int }_{\pi }^{\pi }{\hat{f}}_P(\omega )e^{i\omega x}=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }\sum _{n}f(n)e^{i\omega (x-n)}d\omega .$$

由于$f$很快衰减，于是${\int }_{-\pi }^{\pi }{\sum }_n|f(n)e^{i\omega (x-n)}|d\omega ={\sum }_n|f(n)|<+\infty$，因此可以交换求和与积分运算顺序，于是有
$$f(x)=\sum _{n}f(n)\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{e}^{i\omega (x-n)}d\omega =\sum _{n}f(x)sinc(x-n)$$

对于$s$取其他值，上面的证明过程类似。
定理1的重构公式存在一个问题，它用了一个衰减缓慢且震荡剧烈的$sinc(x)$核函数。在实际应用中，我们很少用这样的核函数的来插值，而是更新换选择更光滑且局部性能更好的核函数。如果$supp(\hat{f})\subset [-\pi /s^{{}^{\prime }},\pi /s^{{}^{\prime }}]$，其中$s^{{}^{\prime }}>s$（也就是，具有更窄的频带），我们也可以重新证明这个采样与重构过程，于是可以具有更多的自由度来设计重构核函数，现在可以选则在频域更窄，在时域指数衰减的核函数。
样条插值函数的定义为：${\varphi }_0=1_{[-1/2,1/2]}$，且${\varphi }_k={\varphi }_{k-1}\ast {\varphi }_0$，它是一个分线多项式函数，阶数为$k$，并且有$k$阶有界导数，在区间$[-(k+1)/2,(k+1)/2]$上紧支撑。采用样条函数作为插值核函数的重构公式为$f(x)\approx \tilde{f}(x)={\sum }_n{a}_n\varphi (x-n)$，其中$(a_n{)}_n$通过$(f(n){)}_n$求解线性系统求得。仅在$k\in 0,1$时有$a_n=f(n)$。在实际经常用的是三次样条插值，对应的$k=3$。

这个理论也解释了在信号$f$的傅里叶变换$\hat{f}$的支撑区间不是$[-\pi /s,pi/s]$时会发生什么。这是会发生信号混叠现象，在支撑区间$[-\pi /s,pi/s]$的高频信号引起低频信号的的混乱叠加，通常称为混叠现象。如果输入信号不是带宽有限的，那么在采样之前进行一个预滤波（平滑），过滤掉频率支撑区间$[-\pi /s,pi/s]$之外的高频信号非常重要，这样可以有效的避免混叠现象。

量化：在已经采集得到信号的离散序列之后，为了能够有效存储和传输，需要把信号用有限精度去量化。后面的信号压缩章节会详细降到如何通过变换编码在变换域中进行高效编码与量化，这对于增强信源编码的性能非常有用。然而，常用的量化策略是直接在采样信号上进行量化操作。

例如，在采样步长为$s=1/N$时，采集到长度问N的信号向量$(u_n=f(n/N){)}_{n=1}^N\in {\mathbb{R}}^N$，由于函数$f$在有限的空间区间与香农采样定理需要函数的傅里叶变换$\hat{f}$也是带宽有限互相矛盾，因为一个函数$f$不可能同时在时间域与频率域同时具有紧支撑特性，因此在有限的存储空间上完美重构信号是不可能的。
选择一个量化步长$T$，量化算子$v_n=Q_T(u_n)\in \mathbb{Z}$在距离$T$的整数倍附近取整，例如
$$v=Q_t(u)\iff v-\frac{1}{2}\le u/T<v+\frac{1}{2},$$

如图1.8所示。恢复信号的过程需要去量化，最好的重构是$D_T(v)=Tv$。量化然后取量化过程引入的最大误差是$T/2$，因为$|D_T(Q_T(u))-u|\le T/2$。量化过程是香农标准过程中唯一的误差引入源。

信号与图像的编码理论后续会单独开一个章节详细讲述，这里暂时略过。
信道编码及纠错码理论是数字通信领域的核心内容，数字通信不是我们研究的重点，后续章节变不会继续论述。

注：未经授权，严谨转载！！！

如有错误或者不解，欢迎批评指正，欢迎私信笔者讨论。