代数——第2章—

第 2 章群(Groups)

II est peu de notions en mathematiques qui soient plus primitives que celle de loi de composition. (数学中很少有比合成律更原始的概念了。)

--------------------------------------------------------Nicolas Bourbaki

2.1 合成律(LAWS OF COMPOSITION)

一个集合S上的一个合成律(law of composition)是一个将S中的元素对 a，b 组合起来以获得集合S 中的另一个元素(比如p)的任意法则(译注：或者理解成一种二元运算法则——将集合S中的元素对映射到集合中的另一个元素上的一种法则)。这个概念的某些模型是实数加法和乘法。n×n 方阵(译注：n×n 方阵或矩阵仅表示这个矩阵是由n行n列个元素构成的，有的书上或者网上译为“n×n 阶方阵或n×n 阶矩阵”具有误导性，“阶”这个词不能乱用，因为它本身有别的含义，后面就会看到；阶用在这里没有任何意义，属于滥用数学术语，引起不必要的混乱，并易使读者迷惑)的集合之上的乘法是合成律的另一个例子。

在形式上，一个合成律就是2个变量的函数，或者一个映射

S × S ⟶ S 。

这里的 S × S 一如既往地表示乘积集(product set)(简称积集)，它的元素是S中的元素对a，b 。

通过将一个定律应用到一个数对a，b 而获得的元素通常采用一个类似于乘法或者加法的符号来书写：

p = ab, a × b，a ∘ b ，a + b ，

或者，无论如何，针对所讨论的(in question)特定定律做出选择。元素 p 可以称为 a 和 b 的乘积或和，具体取决于所选的符号。

大部分情况下，我将选用符号 ab(译注：即，这里的ab不能理解成乘法，而应理解成这两个元素通过某种二元运算生成的集合中另一元素，特定背景或特定说明除外)。使用乘积符号完成的任何操作都可以使用另一种符号(例如加法)重写，并且它将继续有效。重写只是改变了记法。(译注：需要注意的是，集合S是任意集合，不必一定是整数集合或特定集合。)

重要的是要立即注意到，ab 是 S 的某个元素，即，即将以上定律应用到分别用 a 和b 表示的元素上所获得的元素。因此，如果这个合成律是矩阵乘法，且若

$a = \begin{bmatrix} 1 & 3 \\ 0 & 2 \\ \end{bmatrix}$

和

$b= \begin{bmatrix} 1 & 0 \\ 2 & 1 \\ \end{bmatrix}$ ，

则

$ab= \begin{bmatrix} 7 & 3 \\ 4 & 2 \\ \end{bmatrix}$ 。

一旦乘积 ab 完成计算，元素a 和b 就不能从乘积 ab 恢复回来。

根据乘法符号法则，对于一个合成律，若

(2.1.1) (ab)c = a(bc) (结合律(associative law)) ,

对于S 中的所有a，b，c 都成立(其中，(ab) c指第一个乘法(应用这个定律到) a 和b然后再将c乘以第一个乘法的结果ab )，则称这个合成律是可结合的(associative)。

对于一个合成律，如果

(2.1.2) ab = ba (交换律(communicative law))

对于S 中的所有a，b都成立，则称这个合成律是可交换的(communicative)。矩阵乘法是可结合的，但不是可交换的。

对于交换律，习惯于保留加法记法 a + b ——使得对于所有的a，b都有 a + b = b + a 成立的定律(加法可交换)。乘法符号对于交换性没有任何暗示。

结合律比交换律更为基础，原因之一在于，函数的组合是可结合的。令T为一个集合，令 g 和 f 为从 T 到 T 的映射(或函数)。令 g ∘ f 表示复合映射(composed map)t ⇝ g(f(t))(译注：右向波形箭头⇝，Unicode “U+021DD”，LaTex语法“\rightsquigarrow”)：首先应用 f 映射，再应用 g 映射。法则

g ，f ⇝ g ∘ f

是一个映射 T ⟶ T 的集合上的一个合成律。这个定律是可结合的。假如 f ， g 和 h 是三个从 T 到 T 的映射，则 ( h ∘ g ) ∘ f = h ∘( g ∘ f ) ：

这两个复合映射都发送一个元素 t 到h(g(f(t)))。

当 T 包含两个元素的时候，称 T = {a,b} ，从 T ⟶ T 存在4个映射：

i : 恒等映射(identity map)，定义为 i(a) = a, i(b) = b ；

τ : 转置映射(transposition map)，定义为 i(a) = b, i(b) = a ；

α: 常量函数 α(a) = α(b) = a；

β : 常量函数β(a) = β(b) = b 。

基于从 T ⟶ T映射的集合{ i ，τ，α，β } 的合成律可以用一个乘法表(multiplication table)展示：

(2.1.3)

上面的乘法表可以按以下方式解读：

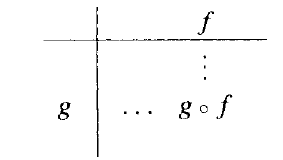
因此，τ ⚬ α = β ，而 α ⚬ τ = α 。

回到组合的一般定律，假设我们想定义一串n个元素连乘构成的集合： $a_1 a_2...a_n = ?$ 使用这个如何乘以两个元素的已知定律，我们可以有多种实现方式。比如，我们可以使用定律首先求得 $a_{1}a_{2}$ , 然后用 $a_{3}$ 来乘以这个元素，如此继续进行下去：

$((a_1 a_2) a_3) a_4 ...$ 。

按照给定的次序，用元素构成乘积，还有几种其它的方式，但是，假如这个定律是可以结合的，则所有这些方式都产生S的相同元素。这就允许我们表述任意一串元素积。

命题 2.1.4 令一个集合的合成律为集合 S 上的已知定律。对于每一个整数 n ，存在对 S中的n 个元素 $a_1 ,a_2,...,a_n$ 之乘的唯一定义，姑且用 $[a_1...a_n]$ 来表示,它具有下列属性：

(i) 一个元素的乘积 $[a_1]$ 是元素本身。

(ii) 两个元素的乘积 $[a_1 a_2]$ 由合成律给出。

(iii) 对于位于 1 ≤ i < n 范围内的任意整数 i ， $[a_1...a_n] = [a_1...a_i][a_(i+1)...a_n]$ 。

(iii) 中的等式意味着，首先构成两个乘积 $[a_1...a_i]$ 和 $[a_(i+1)...a_n]$ ，然后再使用合成律得到结果。

证明：

我们基于 n 做归纳法。对于 n ≤ 2 ，其乘积由 (i) 和 (ii)定义,并且，当 n = 2 的时候，它确实符合 (iii)。我们假设，当 r ≤ n – 1 时，我们已经定了 r 个元素的连乘,并且它是符合 (iii) 的唯一连乘。然后，根据这个规则，我们定义个 n 元素的连乘为

$[a_1...a_n] = [a_1...a_(n-1)][ a_n]$ 。

其中，右边的这些项已被定义。如果符合(iii)的乘积存在，则这个公式给出了乘积，因为当 i = n – 1 时，它正是 (iii) 这种情况。因此，若 n 个元素的乘积存在，它是唯一的。现在，我们必须针对 i < n – 1 检验(iii)是否成立：

$[a_1...a_n] = [a_1...a_(n-1)][ a_n]$ (由定义)

$[a_1...a_n] = ([a_1...a_i][ a_(i+1)...a_(n-1)])[ a_n]$ (归纳假设)

$[a_1...a_n] = [a_1...a_i]([ a_(i+1)...a_(n-1)][ a_n])$ (结合律)

$[a_1...a_n] = [a_1...a_i]([ a_(i+1)...a_n])$ (归纳假设)。

这就完成了证明。从此，我们去掉括号，并用 $[a_1...a_n]$ 表示连乘。

一个合成律的幺元(identity)(译注：即，单位元素)是集合S中的一个元素e ,它使得对于S中的任意元素a , 都有

ea = a且 ae = a 。

至多可以存在一个恒等式，因为，若 e 和 e’ 是两个这样的元素，则，因为 e 是一个幺元， e e’ = e’ , 并且，因为 e’ 也是一个幺元，则 e = e e’ 。因此，e = e e’ = e’ 。

函数的矩阵乘法和复合都有一个幺元。对于 n×n 矩阵而言，幺元是单位矩阵 I ，而对于 T ⟶ T 的映射集合而言，幺元是恒等映射——将每个T元素映射到其自身。

若采用乘法合成律，则幺元元素表示为1；若采用加法合成律，则幺元元素表示为0 , 这些元素不需要与数 1 和 0 相关，但由于它们的合成律，它们共享幺元元素的属性。

假设采用乘法合成律的一个集合 S 上的合成律是可结合的且有一个幺元1，则对于S 中的一个元素a，若存在另一个元素b 使得

ab = 1 和 ba = 1 ，

则称S 中的这个元素 a 可逆(invertible)，且若如此，则称元素b为元素a的逆元(inverse)。一个元素的逆元通常表示为 $a^{-1}$ ，或者当应用于加法时，表示为 -a。

我们列出逆元的某些元素属性，在此不加证明。除了最后一个属性之外，其余所有属性都已经针对矩阵讨论过。有关说明最后一条表述的示例，请参见练习 1.3。

$\bullet$ 若一个元素 a 既有一个左逆元 𝓁 ，对具有一个右逆元 r，即，𝓁a = 1且 ar = 1，则 𝓁 = r ，a 可逆。

$\bullet$ 若 a 可逆，则其逆元是唯一的。

$\bullet$ 逆元按反序相乘：若 a 和 b可逆，则其乘积 ab 也可逆，且 $(ab)^{-1} = b^{-1} a^{-1}$ 。

$\bullet$ 一个元素 a ，即便其本身不可逆，它也可以有左逆元或右逆元。

幂记法可以用于结合律：n > 0 , $a^n = a...a$ (n 个因子)， $a^{-n} = a^{-1}... a^{-1}$ , 且 $a^{0} = 1$ 。操控幂的常规法则仍然成立： $a^r a^s = a^{r+s}$ 和 $(a^r)^s = a^{rs}$ 。当加法符号被用于合成律时，幂记法 $a^n$ 被替换为 na = a + ... + a 。

若非合成律是可交换的，否则不推荐分数记法 $\frac{b}{a}$ ，因为这种记法是不明确的，根据这种记法，无法判断这个分数记法是表示 $ba^{-1}$ ，还是表示 $a^{-1}b$ ，而这两种表示法的元素可能是不同的。

2.2 群和子群及相关概念(GROUPS AND SUBGROUPS)

(译注：“群(group)”和“群论(group theory)”这两个术语是由群论的创建人，法国数学家Evariste Galois(伽罗瓦)引入的。群论的思想在Galois之前就已有流传(就像最基本的数学思想产生时常有的情况那样)，Lagrange事实上已经证明了群论的一些定理，虽然其形式是朴素的。Galois天才的工作起初并没有被人们理解，对这一工作重又引导起兴趣是在Jordan的书<<置换和代数方程>>(1870年)出版之后开始的。直到19世纪末，群论才“完全脱离了梦幻，代之以精细整理过的逻辑结构。” )

一个群(group)是一个集合G 与一个基于集合G的合成律的结合体，且这个合成律具有以下属性：

$\bullet$ 这个合成律是可结合的(associative)：对于集合G中的任意元素 a , b , c ,有 (ab)c = a(bc)。

$\bullet$ 集合G包含一个幺元元素1 ，使得对于集合G中的任意元素 a ,有 1a = a 且 a1 = a 。(译注：可能作者为了方便表述，使用了1来表示单位元；事实上，作者真实意图是表示存在幺元或称单位元e(我们姑且用e来表示单位元)，使得对于集合G中的任意元素 a ,有 ea = ae = a。)

$\bullet$ G的每一个元素a都具有一个逆元(inverse)，即有一个对应的元素b，使得 ab = 1 且 ba = 1 。(译注：同上，这里的1表示单位圆；事实上，指的是存在一个对应的元素b，使得 ab = ba = e 。)

(译注：有的书上还定义了半群(semi-group)——在以上定义中，仅满足第一条可结合条件的情况。)

一个Abel群是一个合成律可交换的(commutative)群。

例如，非零实数的集合与乘法定律构成一个Abel群，以及所有实数的结合与加法定律构成一个Abel群。n×n 可逆矩阵的集合，构成一般线性群，这是一个非常重要的群，其中的合成律是矩阵乘法，除 n = 1 这种情况,它不是Abel群。

当群的合成律是显而易见的时候，习惯于用同一符号表示群及其元素的集合。

一个群G的阶数(order)指的是群中元素的数量(译注：注意，在不至于引起混淆的背景下，可以将“阶数”简称为“阶”，但是必须谨记，集合和群中的“阶数”或“阶”，指的是元素的数量，并不是“等级”)。我们通常用|G|表示群G的阶数：

(2.2.1) | G | = 群 G 所包含的元素的数量。

如果群 G 的阶数是有限的，则称群 G 是一个有限群(a finite group)。否则，称G是一个无限群(an infinite group)。相同的术语可用于任意集合，比如，一个集合 S的阶数|S|是其元素的数量。

以下是我们使用的对一些我们所熟悉的无限Abel群的记法：

(2.2.2)

$\mathbb{Z}^{+}$ ：整数的集合，带加号是因为其合成律是加法——表示整数的加法群。

$\mathbb{R}^{+}$ ：实数的集合，带加号是因为其合成律是加法——表示实数的加法群。

$\mathbb{R}^{\times }$ ：非零实数的集合，带乘号是因为其合成律是乘法——表示非零实数的乘法群。

$\mathbb{C}^{+}$ , $\mathbb{C}^{\times}$ ：与上面对应的群类似，只是用复数ℂ代替了实数ℝ。

注意：别的地方可能用了符号 $\mathbb{R}^{+}$ 来表示正实数的集合。为了避免混淆，最好将实数的加法群表示为 (ℝ ,+), 因此，显式地表明了其合成律。然而，我们前面的记法更为精简。此外，符号 $\mathbb{R}^{\times }$ 表示非零实数的乘法群。所有实数的集合和乘法定律不构成群，因为0不可逆。

命题 2.2.3 消去律(Cancellation Law) 令 a , b , c 为采用乘法合成律的群 G 的元素。若 ab = ac 或者 ba = ca ，则 b = c 。若 ab = a 或 ba = a ，则 b = 1 。

证明：

在等式 ab = ac 的两边的左侧分别乘以 $a^{-1}$ 而得到 b = c。其它等式的证明类似。乘以 $a^{-1}$ 对这个证明至关重要。当元素a不可逆的时候，消去律一定不成立。例如，

$\begin{bmatrix} 1 & 1 \\ & \\ \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 2 & \\ \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ & \\ \end{bmatrix} \begin{bmatrix} 3 & \\ & 1\\ \end{bmatrix}$ 。

群的2个基本例子可以通过我们已经考虑过的合成律获得——矩阵乘法和函数复合——通过省略不可逆元素。

n × n 一般线性群(general linear group)是所有可逆 n × n 矩阵的群。表示为

(2.2.4) $GL_n$ = { n×n 可逆矩阵A } 。

根据具体的情况，如果我们想表明我们正在使用实数或者复数矩阵，我们写成 $GL_{n}(\mathbb{R})$ 或 $GL_{n}(\mathbb{C})$ 。

令 $M$ 为从集合T到其自身的映射的集合。对于一个映射 $f :T \longrightarrow T$ , 当且仅当这个映射是双射(bijective)的时候，这个函数f具有一个逆函数，在这种情况下，我们称f是T的置换(permutation)。 $T$ 的这种置换构成一个群，即映射的合成律。如果在1.5节讲的那样，我们用乘法记法表示置换的组合，将 q ⚬ p 写成 qp 。(译注：再次注意，这只是二元运算的记法，并不表示乘法或某具体运算。)

$\bullet$ 索引 {1，2，...，n} 的集合构成的置换群称为对称群(symmetric group)，并用 $S_n$ 表示为：

(2.2.5) $S_n$ 是索引{1，2，...，n } 的集合构成的置换群。

n个元素的集合的置换数有n!个。因此，对称群 $S_n$ 是阶数为 n! 的有限群。

两个元素的集合{ a , b } 的置换是幺元i 和转置(transposition) τ (参见2.1.3)。它们构成了2阶群。如果我们将a替换为1, b 替换为2,我们看到，这个群与 $S_2$ 是同一个群。在本质上，2阶群G只有一个。为了理解这一点，我们注意到，其元素之一一定是玄元1；令其中的其它元素为g。群的乘法表包含四个乘积11,1g，g1,和gg。在这四个乘积中，除了 gg，其它三项事实上均由幺元1确定。此外，消去律表明 gg ≠ g,唯一的可能性是 gg = 1。因此，乘法表是完全确定的，只有一条群定律。

接下来我们描述对称群 $S_3$ 。对称群 $S_3$ 的阶是6, 这正好作为一个方便的例子，因为它是合成律不可交换的最小群。我们会频繁引用它。为了描述它，我们根据其可以写成所有其它项的原则挑两个特别的置换。我们取循环置换(cyclic permutation)(123)，和置换(12),并分别将其标为x和y。规则

(2.2.6) $x^3 = 1,y^2 = 1 , yx = x^2y$

容易验证。使用消去律，读者可以看到，这6个元素 $1,x, x^{2},y,xy,x^{2}y$ 是不同的。因此，它们是群

(2.2.7) $S_3 = \{ 1,x,x^{2};y,xy,x^{2}y\}$

的6个元素。在后面，我们会将(2.2.6)和(2.2.7)称为我们的对称群 $S_3$ 的“常规呈现(usual presentation)” 。注意， $S_3$ 是不可交换群，因为 yx ≠ xy 。

规则(2.2.6)足以实现计算。通过反复地应用规则(2.2.6),可以证明元素 x和 y的任意乘积和其逆元的任意乘积等于乘积(2.2.7)之一。要做这样的操作，使用最后一个规则，我们将所有出现y的地方移到右边，我们使用前两条规则来保持指数较小。例如：

(2.2.8) $x^{-1}y^3 x^2 y=$ $x^2 yx^2 y = x^2(yx)xy = x^2(x^2y)xy = xyxy = x(x^2y)xy = 1$

读者在规则 (2.2.6) 的帮助下可以写出 $S_3$ 的乘法表，由于这个原因，这些规则被称为群的定义关系(defining relations)。我们将在第7章学习定义关系。此处我们暂且介绍到这里。随着n 的递增， $S_n$ 的结构迅速复杂化。

一般线性群和对称群很重要，其原因之一在于，它们中包含了很多作为子群的其它群。对于一个群 G的子集合H，如果它具有后面所列出的属性, 则称 H 是一个子群(subgroup)；这些属性是：

(2.2.9)

$\bullet$ 闭合性(Closure)：若 a和 b在 H中，则 ab 也在H 中(译注：注意，ab 表示二元运算，不特指乘积)；

$\bullet$ 存在幺元(Identity): 1 在 H中(译注：如前所述，表示单位元e在H中)；

$\bullet$ 存在逆元(Inverse): 若 a 在 H 中，则 $a^{-1}$ 也在H 中。

这些条件解释如下：第一个条件告诉我们，群 G上的一个合成律定义了H上的一个合成律，称为诱导法则(induced law)。第二和第三个条件指的是，针对这个诱导法则，H是一个群。注意，(2.2.9)提及了群定义中除去结合律的所有方面。我们不必在此提及结合律，因为从G到子集合H自动地留存(carries over)了结合律。(译注：有的书上使用 H ≤ G表示这种子群关系。)

注意：

(i) 在数学中，学习每一个术语的定义是最基本的一个环节，且仅靠直觉是不够的。例如，可逆的实(上)三角 2×2 矩阵的集合T 是一般线性群 $GL_{2}$ 的子群，且仅有一种验证方式,即，回到子群的定义去验证。事实上，T 的确是一般线性群 $GL_{2}$ 的子群。你必须验证可逆三角矩阵的积是三角矩阵，即，幺元是三角矩阵。并验证可逆三角矩阵的逆元也是三角矩阵。显然，这些要点很容易验证。

(ii) 有时候，将闭合性作为群的公理之一，以表明 G 的元素的乘积 ab 又是 G 的一个元素。我们将闭性合作为合成律的一部分。那么就不需要在群的定义中重述了。

示例 2.2.10：

(a) 绝对值(译注：absolute value，或称模(modulus))为1的复数集，即在复平面上单位圆周上的点集，是乘法群 $\mathbb{C}^{\times}$ 的一个子群，称为圆周群(circle group)。

(b) 具有行列式(determinant)1的实数 n×n 矩阵是一般线性群 $GL_{n}$ 的一个子群，称为特殊线性群(special linear group)。用 $GL_{n}$ 表示：

(2.2.11) $SL_{n}(\mathbb{R})$

是具有行列式等于1的实n×n 矩阵A集合。

定义属性 (2.2.9)通常很容易验证为一个特殊群，我们可能不会验证。

每一个群G都有两个明显的子群：群 G自身，以及由幺元单独构成的平凡子群(trivial subgroup)。如果一个子群不是以上两种情况之一，则称其为真子群(proper subgroup)。

2.3 整数加法群的子群(SUBGROUPS OF THE ADDITIVE GROUP OF INTEGERS)

在这里，我们根据整数加法群 $\mathbb{Z}^{+}$ 的子群，回顾一些初等数论的知识。我们以列出当加法记法被用于群中时的子群的公理开始：对于一个具有加法合成律的群G的子集S，如果其具有后面所列出的属性，则称集合S是一个子群(译注：整数加法群)；这些属性是：

(2.3.1)

$\bullet$ 闭合性(Closure)：若 a 和 b在 S 中，则 a + b 也在S 中；

$\bullet$ 存在幺元(Identity): 0 在 S 中；

$\bullet$ 存在逆元(Inverse): 若 a 在 S中，则 $a^{-1}$ 也在S 中。

令 a 为不同与0的整数，我们用 ℤa 表示由所有a的倍数组成的ℤ的子集：

(2.3.2) ℤa = { n∈ℤ |对于ℤ中的某个k，有 n = ka } 。

这是加法群 $\mathbb{Z}^{+}$ 的一个子群。其元素也可以表述为被a整除的整数。

定理 2.3.3 令 S 为加法群 $\mathbb{Z}^{+}$ 的一个子群。则 S 要么是平凡子群 {0} ，要么就是具有形如 ℤa 形式的群，其中，a 是 S 中的最小正整数。

证明：

令 S 为加法群 $\mathbb{Z}^{+}$ 的一个子群。则 0 在S 中，若 0是中的唯一元素，则 S 是平凡子群(译注，根据平凡子群的定义)。因此，这种情况解决。否则，S 包含一个不同于0的整数n，且 n 或 –n 是正整数。子群的第三个属性告诉我们，–n 在S中，因此，在任一种情况下，S都包含正整数。我们必须证明，当a是S中的最小正整数时，S 等于ℤa。

我们首先证明ℤa是S的一个子集，换句话说，证明对于每一个整数k，ka在S中。若k是一个正整数，则 ka = a + a + ... + a (k项)。因为a在S中，闭合和归纳可证明ka在S中。因为逆元在S中，因此，- ka在S中。最后，0 = 0a在S中。

接下来，我们证明S是ℤa的一个子集，即，S的每一个元素n都是a的整数倍。我们使用带余除法表达式写成 n = qa + r (其中，q是r是整数且 0 ≤ r <a)。因为 ℤa包含于S中，所以，qa也在S中，且显然，n 在S中。因为S是一个子群，r = n – qa 也在S中。现在，根据我们的选择，a是S中最小的正整数，而余数r的范围位于0 ≤ r <a 之间。因此，可以位于S中的余数唯有0。因此，r = 0 且 n 是 a的整数倍qa 。

定理 2.3.3 在包含两个整数 a 和 b 的子群上有一个引人注目的应用。a 和 b 的所有整数组合 ra + sb 的集合，

(2.3.4) S = ℤa + ℤb = { n∈ℤ | 对于某些整数 r ，s ，有 n = ra + sb }

是 $\mathbb{Z}^{+}$ 的一个子群。称为由a 和 b产生的子群，因为它是包含a 和 b 两者的最小的群。我们假设 a 和 b并不同时为0，因此，S不是平凡群{0}。定理 2.3.3告诉我们，对于某个正整数d，子群 S 具有形式 ℤa ；它是可被d 整除的整数集。整数d被称为a 和 b的最大公约数(greatest common divisor，最大公共除数)，至于原因，在下一个命题的(a)和(b)项中作说明。有时候，a 和 b 的最大公约数记为gcd(a, b)。

命题 2.3.3 令 a 和 b为整数，且不同时为0，令d为它们的最大公约数(即，产生子群S = ℤa + ℤb 的正整数)。因此有 ℤd = ℤa + ℤb 。则

(a) d 整除a 和 b ；

(b) 若一个整数e 整除 a 和 b ，则它也整除 d；

证明：

(c)部分重述了d是S的一个元素的事实。然后，a 和 b是S的元素且 S = ℤd ，因此，d整除 a 和 b 。最后，若整数e整除 a 和 b ，则e整除整数组合 ra + sb = d 。

注意：若整数e整除 a 和 b ，则整数e整除任意形如 ma + nb的整数。因此，(c)就意味着(b),但(b)并不意味着(c)。正如我们将看到，属性(c)是一个强有力的工具。

读者可以通过反复使用余数相除法很容易地计算出最大公约数：例如，若 a = 314 ，b = 136 ，则

314 = 2.136 + 42，136 = 3.42 + 10 ，42 = 4.10 + 2 。

使用这些等式中的第一个，读者可以表明，314 和 136 的任意整数组合都可以写为136和余数42的任意整数组合，反之亦然。类似地，gcd(136,42 ) = gcd(42,10 ) = 2 。因此，314 和 136 的最大公约数是2。这种求解两个整数的最大公约数的迭代法(重复法)称为Euclid 算法(Euclidean Algorithm)。

若已经 a 和 b ，求解它们的最大公约数的第二种方法是将其每一个整数分解为素数因子，然后收集其公共素数因子。使用这种方法，很容易验证命题 2.3.5 的属性(a)和(b)。但若没有定理2.3.3，属性(c)(用这种方法所确定的整数a 和 b 的一个整数组合)一点也不明确。在此，我们跳过对这个点的讨论,在第12章再回到对这个问题的探讨。

对于这两个非0整数 a 和 b ，如果能够整除它们的正整数只有1，则称其为相对素数(relative prime)。则它们的最大公约数是1 ： ℤa + ℤb = ℤ。

引理 2.3.6 对于一个整数对 a ，b ，当且仅当存在整数 r和 s ，使得 ra + sb = 1 成立时，这个整数对是相对素数。

引理 2.3.6 令p为一个素数整数，若 p 整除一个整数积ab ，则p整除a和整除b。

证明：

假如素数p整除 ab但不整数a。则 p的正除数只可能是1和p。因为p不整除a，则gcd(a,p ) = 1 。因此，存在整数 r和 s ，使得 ra + sp = 1 。我们在等式两侧乘以 b ：rab + spb = b ，并注意到，p整除rab和spb 。因此，p 整除b 。

存在另一个与整数对 a ，b 相关的 $\mathbb{Z}^{+}$ 的一个子群，即交叉群 ℤa ∩ ℤb ，既包含于ℤa又包含于ℤb之中的整数构成的集合。现在我们假设 a 和b都非0 。则 ℤa ∩ ℤb 是一个子群。它不是平凡群 {0}，因为它包含了乘积ab，而这个整数不为0。因此，对于某个正整数m，子群 ℤa ∩ ℤb 具有ℤm 的形式。这个整数m被称为整数a 和 b的最小公倍数(least common multiple),有时候记为 lcm(a，b)，到于原因，将在下一个命题中解释。

命题 2.3.8 令 a 和 b为不同于0的整数，令m为它们的最小公倍数(即，产生子群S = ℤa ∩ ℤb 的正整数)。因此有 ℤm = ℤa ∩ ℤb 。则

(a) m能被a 和 b 整除；

(b) 若一个整数n 能被a 和 b 整除，则它也能被m整除；

证明：

以上两条表述都可以基于后面的事实推导出来——一个整数能被a 和 b 整除的前置条件是，当且仅当它包含于 ℤm = ℤa ∩ ℤb 之中。

引理 2.3.9 令 d = gcd(a，b) 和 m = lcm(a，b)分别为一个整数对 a ，b的最大公约数和最小公倍数。则 ab = bm 。

证明：

因为 b / d 是一个整数，所以，a整除ab / d 。类似地，b整除ab / d 。因此，m整除ab / d ，且 dm整除ab 。下一步，我们写成 d = ra + sb 。则 dm = ram + sbm 。右边的两项均可被ab整除，因此，ab整除dm。因为ab整除dm都是正值且互相可整除，所以 ab = bm 。

2.4 循环群(CYCLIC GROUPS)

现在，我们开始接触一个重要的抽像子群例子——由一个群G的一个任意元素x所产生的循环子群(cyclic subgroup)。我们使用乘法符号。由x所产生的循环子群H是x的幂的所有元素的集合：

(2.4.1) $H = \{...,x^{-2}, x^{-1}, 1 , x, x^{2} ,...\}$ 。(译注：此处1指单位元 e 。 )

这是含有x的G的最小子群，通常记为 <x>。但是，为了正确地解释(2.4.1)，我们必须牢记，记法 $x^{n}$ 表示按一种特定方式所获得的群的一个元素。不同的幂符号可以表示相同的元素。例如，G 是乘法群 $\mathbb{R}^{\times}$ 且 x = -1 ,则列表中所有的元素等1或等于-1，H 就是集合{1，-1}。

存在两种可能：幂 $x^{n}$ 表示不同的元素，或表示相同的元素。我们分析x的幂不同的这种情况。

命题 2.4.2 令 <x> 为由元素x所产生的群 G 的循环子群，并令 S 为使得 $x^{k} = 1$ 的整数k 的集合。

(a) 集合S 为加法群 $\mathbb{Z}^{+}$ 的一个子群。

(b) 对于两个幂 $x^{r},x^{s}$ 且 r ≥ s ，当且仅当 $x^{r-s}=1$

时(即，当且仅当 r - s在S中时)，它们是相等的。

(c) 假设S不是平凡子群。则，对于某个正整数 n，S = ℤn 。幂 $1 , x, x^2 ,..., x^{n-1}$

是子群 <x> 中不同的元素, <x> 的阶数是 n 。

证明：

(a)：若 $x^k = 1$ 且 $x^{\ell}=1$ ，则 $x^{k+\ell} = x^{k}x^{\ell}=1$ 。这证明了，若 k和 𝓁 在 S 中，则 k + 𝓁 在 S 中。因此，子群的属性(2.3.1)的第一个得到验证。此外， $x^{0}=1$ ，因此，0 在 S 中。最后，若 k 在 S 中，即， $x^k = 1$ , 则 $x^{-k} =(x^{k})^{-1}= 1$ ，因此，-k 也在 S 中。

(b)：可以从消去律 2.2.3推导出。

(c)：假设 S ≠ {0}, 定理2.3.3证明，S = ℤn ，其中，n 是S中的最小正整数。若 $x^{k}$ 是任意幂，我们用n整除k，写成 k = qn + r 且 q 介于 0 ≤ r < n 之间，则 $x^{qn} = 1^q = 1$ ，且 $x^k = x^{qn} x^r = x^r$ 。因此， $x^{k}$ 等于幂 $1 , x, x^2 ,..., x^{n-1}$ 之一。从(b)可以推导出，这些幂是不同的，因为是等于1的最小正幂。

由这个命题的(c)部分所描述的群 $< x > = {1 , x, x^2 ,..., x^{n-1} }$ 阶数为n的循环群。称其为循环是因为，使用x的重复乘法循环执行直至产生n个元素。(译注：有的书上称 x 为对应群的生成元。)

若n是具有属性 $x^{n}=1$ 的最小正整数，则群的元素 x 具有阶数n ，这与称循环子群 < x > 由有n 阶的 x 产生等价。

按照对称群 $S_{3}$ 的常规表示，元素 x 具有阶数3，y具有阶数2。在任意群中，幺元元素是唯一的阶数为1的元素。

若对任意 n > 0 ， $x^{n} \neq 1$ ，则称 x 具有无限阶数。群 $GL_{2}(\mathbb{R})$ 中的矩阵

$\begin{bmatrix} 1 & 1 \\0 & 1\\ \end{bmatrix}$

具有无限阶数，而

$\begin{bmatrix} 1 & 1 \\-1 & 0\\ \end{bmatrix}$

具有阶6 。

当 x 具有无限阶数的时候，群 < x > 称为无限循环群(infinite cyclic group)。对这种情况，我们不作过多讨论。

命题 2.4.3 令 x 为一个群中具有有限阶数n 的一个元素，并令 k 为写成 k = qn + r 的整数，其中，q 和 r 是整数，且 r 介于 0 ≤ r < n 之间。则

$\bullet$ $x^{k}=x^{r}$ 。

$\bullet$ 当且仅当 r = 0 时， $x^k=1$ 。

$\bullet$ 令 d 为 k和 n 的最大公约数。 $x^k$ 的阶数等于 n / d 。

也可以说，这个G的子群是由一个子集U所产生。这是包含U的G的最小子群，并且，它包括所有可以表示为U的一串元素的连乘和其一串逆元的连乘的G的元素。如果G的每一个元素是这样的乘积，则称G的子集U 生成(generate)G。例如，我们看到在(2.2.7)中，集合 U = {x，y } 产生对称群 $S_{3}$ 。初等矩阵产生 $GL_{n}$ (1.2.16)。在这两个例子中，不需要逆元。但并不总是这样。一个无限循环群 < x > 由元素 x 生成，但是需要负幂填满整个群。

Klein四元群(The Klein four group)V，即，由四个矩阵组成的群

(2.4.4)

$\begin{bmatrix} \pm 1 & \\ & \pm 1\\ \end{bmatrix}$ ，

是最简单的非循环群。其不同于幺元元素的任意两个元素生成V。四元群(The quaternion group) H是另一个小群的例子。它由8个矩阵构成，即

(2.4.5) $H = \{ \pm l ,\pm i,\pm j, \pm k\}$ ，

其中，

$l=\begin{bmatrix} 1 & \\ & 1\\ \end{bmatrix}$ , $i=\begin{bmatrix} i & \\ & -i \\ \end{bmatrix}$ , $j=\begin{bmatrix} & 1\\ -1 & \\ \end{bmatrix}$ , $k=\begin{bmatrix} & i \\ i & \\ \end{bmatrix}$ 。

这些矩阵可以通过物理的Pauli矩阵乘以i 而获得。 i 和 j 这两个元素生成 H 。计算导出了公式

(2.4.6) $i^2 = j^2 = k^2 = -1 , ij = -ji = k,jk = -kj = i,ki = -ik = j$ 。

2.5 同态(HOMOMORPHISMS)

(译注：词homomorphism[ˌhəʊməʊˈmɔːfɪzəm]，由homo- +希腊词根μορ-ή 形式+ -ism 构成。homo-的词义为“same, the same, equal, like(同，相同，相等，相似)”；而 morphic 指，在生物学上，“of or pertaining to form(关于或属于某种形式)”,来自希腊词“morphē ”，其词义为“form(形式),shape(形状)”；合起来词义便是“相同的某种形状”。在数学上，homomorphism和homomorphic被发现出现在1921年的 <<Primitive Groups Part I>>(本原群第一部分)中，作者William Albert Manning。) 牛津词典对应的数学词条解释为“A many-to-one (or one-to-one) transformation of one set into another that preserves in the second set the operations or relations between the elements of the first(一个集合到另一个集合的多对一(或一对一)转换，并在第二个集合中保留第一个集合的元素之间的运算或关系)。”实际上就是在不改造原有群结构的前提下进行映射。汉译“同态”并不能准确地传达这种关系。

令 G 和 G’ 为两个群，使用乘法记法(译注：如上，只是表示一种合成律)。一个同态 φ ：G ⟶ G’，是一个从G 到G’ 的映射，且这个映射使得对于G中的任意元素 a 和 b ，都有

(2.5.1) φ(ab) = φ(a) φ(b) 。(译注：能满足这种关系的映射就能保证2个采用不同合成律的群之间产生联系。)

这个等式的左侧指的是，首先在G中将 a和b相乘(译注：也可能是相加，或者别的二元远算)，然后使用映射 φ 将乘积发送到G’，而等式的右侧指的是，首先使用映射 φ 将分别将a和b发送到 G’，然后再将在G’中的像(images)相乘。

在直观上，同态是一种与两个群中合自的合成律兼容的映射，它提供了一种在不变动原有群结构的基础上将不同的群关联起来的方式。(译注：同态是一种在不改动原有两个群各自结构的基础上,在两个群之间建立起来的映射关系；比如群G采用的合成律是加法，而群 G’采用的合成律是乘法，则通过这种从G到G’的映射关系(称为同态映射),两个群之间的元素产生了对应关系(像与原像的关系)。)

例子 2.5.2 下面的映射是同态：

(a) 行列式(determinant)函数 $\det:GL_n(\mathbb{R}) \longrightarrow \mathbb{R}^{\times }$ (1.4.10)，

(b) 符号同态(sigh homomorphism) $\sigma:S_{n} \longrightarrow {\pm 1}$ ，其将一个置换(permutation)发送到其符号(1.5.11)，

(c) 由 $x \rightsquigarrow e^{x}$ 所定义的指数映射 $\exp: \mathbb{R}^{+} \longrightarrow \mathbb{R}^{\times}$ (译注：右向波形箭头的Unicode值为“U+021DD”，LaTex语法为“\rightsquigarrow”)，

(d ) 由 $\varphi(n) = a^{n}$ 所定义的映射 $\varphi:\mathbb{Z}^{+} \longrightarrow G$ ，其中a是G的一个已知元素，

(e) 绝对值映射||: $\mathbb{C}^{\times } \longrightarrow \mathbb{R}^{\times }$ 。

在例子(c)和(d)中，合成律是域(domain)中的加法和范围(range)内的乘法。同态的条件(2.5.1)现在应显式写成加法。重写后变成了

φ(a + b) = φ(a) φ(b) 。

这个公式表明，指数映射是一个同态 $e^{a+b}=e^{a}e^{b}$ 。

必须提及下面的同态，尽管他们不那么有趣。任意两个群之间的平凡同态(trivial homomorphism)映射 φ ：G ⟶ G’，其将G中的每一个元素映射到G’中的幺元元素。若H是G的一个子群，则由针对H 中的元素i 的关系i(x) = x 所定义的包含映射(inclusion map) i : H⟶ G ，是一个同态。

命题 2.5.3 令 $\varphi :G \longrightarrow G'$ 为一个群同态。

(a) 若 $a_1 , a_2 ,..., a_k,$ 是G中的元素，则 $\varphi(a_1... a_k) = \varphi(a_1)... \varphi(a_k)$ 。

(b) φ映射幺元到幺元： $\varphi(1_G) = \varphi(1_(G'))$ (译注： $1_G$ 和 $1_G'$ 都表示各自群中的幺元)。

(c) φ映射逆元到逆元： $\varphi (a^{-1}) = \varphi(a)^{-1}$ (译注：即，若 $\varphi(a) = h$ , 则 $\varphi(a)^{-1} = h^{-1}$ ) 。

证明：

第一个诊断按归纳法由定义可推导。然后，因为 1.1 = 1 且因为φ 是一个同态，φ(1)φ(1) = φ(1.1) = φ(1)。我们根据消去律(2.2.3),在前面等式两侧消去一个φ(1)，便求得 φ(1) = 1 。最后， $\varphi(a^{-1}) \varphi(a) = \varphi(a^{-1} a) = \varphi(1) = 1$ 。因此， $\varphi(a^{-1})$ 是 φ(a) 的逆元(译注：即 $\varphi(a)^{-1}$ )。

一个群同态确立了两个重要的子群：同态的像(image)和同态的核(kernel)。

$\bullet$ 一个同态 φ ：G ⟶ G’ 的像(通常用 im φ表示)只是 φ 作为集合映射的像：

(2.5.4) im φ = { x∈G’| 对于G中的某个a，有 x = φ(a)}，

像的另一种记法是 φ (G )。

发送 $n \rightsquigarrow a^{n}$ 的映射 $\mathbb{Z}^{+} \longrightarrow G$ 的像是由 a 生成的循环子群 < a >。

一个同态的像是范围(range)的子群。我们将验证闭合性，并忽略其它验证。令 x和 y为像的元素。这指的是，存在G中的元素a和b，使得 x = φ(a) 和 y = φ(b)。因为φ 是一个同态，xy = φ(a) φ(b) = φ(ab) 。因此 xy = φ(something)。它也在像中。

$\bullet$ 一个同态的核(kernel)更为精细且更为重要。φ的核(通常用ker φ 表示)是被映射到G’中的幺元上的G的元素的集合：

(2.5.5) ker φ = { a∈G | φ(a) = 1 }。(译注：同上，1指单位元e 。)

核是G的一个子群，因为，若 a和b在核中，则，φ(ab) = φ(a) φ(b) = 1.1 = 1 ，因此，ab在核中，等等。

行列式同态 $GL_n(\mathbb{R}) \longrightarrow \mathbb{R}^{\times}$ 是特别的线性群 $SL_n(\mathbb{R})$ (2.2.11)。符号同态 $S_n \longrightarrow \{ \pm1\}$ 被称为交替群(alternating group)。它由偶置换(even permutations)组成，用 $A_{n}$ 表示：

(2.5.6) 交替群 $A_{n}$ 是偶置换群。

核非常重要，原因在于它控制着整个同态。它不仅告知了我们G中的哪些元素被映射到G’的幺元，而且还告知了我们G中的哪些元素对在G’中具有相同的像。(译注：既然核这么重要，那么我可以将术语“kernel”理解为群同态的“核心”，简称“核”，这或许就是这个术语的含义所在。)

$\bullet$ 若H是群G的一个子群，且a是G的一个元素，记法 aH 表示a与H中所有h的乘积ah的集合：

(2.5.7) aH = { g∈G |对于H中的某个h，g = ah } 。

这个集合称为G中H的左陪集(a left coset，或称左䧛集)(译注：“䧛”在汉语中是“近”的意思，似乎用在这里不是很贴切)，在这里，“left” 这个词指出了元素a出现在左边的事实。

命题 2.5.7 令φ ：G ⟶ G’ 为一个群的同态，并令 a 和 b 为G 中的元素。令 K 为φ 的核。则下面的条件是等价的：

$\bullet$ φ(a) = φ(b)，

$\bullet$ $a^{-1}b$ 在K 中，

$\bullet$ b 在左陪集 aK 中，

$\bullet$ 陪集 aK 和 bK 是相等的。

证明：

假设 φ(a) = φ(b)。则 $\varphi(a^{-1}b) = \varphi(a^{-1}) \varphi(b) = \varphi(a)^{-1}\varphi(b) = 1$ 。因此， $a^{-1}b$ 在核 K 中，为了证明其逆也成立，我们将参数倒过来。若 $a^{-1}b$ 在核 K 中，则 $1=\varphi(a^{-1}b)=\varphi(a)^{-1}\varphi(b)$ ,因此φ(a) = φ(b)。这就证明了前面两个实心黑点所标示的条目是等价的。它们也其后的条目也等价。

引理 2.5.9 对于同态φ ：G ⟶ G’，当且仅当其核K是G的平凡子群{1}时，它是单射的(injective)。

证明：

若 { K } = 1 ,命题 2.5.8证明了，仅当 $a^{-1}b=1$ 时(即当 a = b 时)， φ(a) = φ(b)。相反，若φ 是单射的，则幺元是使得φ(a) = 1 的G的唯一元素，因此，{ K } = 1。

同态的核的另外一个重要的属性将在下一个命题中解释。若 a和g是群G的元素，元素 $gag^{-1}$ 被称为a按g 的共轭。

定义 2.5.10 对于一个群G的子群N ，若对于N中的每一个a和G中的每一个g，共轭 $gag^{-1}$ 都在N中，则称N是一个不变子群(invariant subgroup，原因在于，这个子群在其所属群的成员共轭下保持不变)(译注：另外还有2个名称，normal subgroup(有些数学术语书上译为“正规子群”，似乎不妥，词不达意，译为“常规子群”似乎更妥)；又称自共轭子群(self-conjugate subgroup))。

命题 2.5.11 一个同态的核是一个不变子群。

证明：

若 a在同态φ ：G ⟶ G’的核中，且若 g是 G中的任一元素，则 $\varphi(gag^{-1}) = \varphi(g) \varphi(a) \varphi(g^{-1}) = \varphi(g) 1 \varphi(g^{-1}) = \varphi(g)1 \varphi(g)^{-1} =1$ 。(译注：利用同态映射逆元到逆元的性质 $\varphi (g^{-1}) = \varphi(g)^{-1}$ 。) 因此， $gag^{-1}$ 也在核中(译注：根据核的概念，被映射到1上)。

因此，特殊线性群 $SL_n(\mathbb{R})$ 是一个一般线性群的子群，而交替群 $A_{n}$ 群是对称群 $S_{n}$ 的一个一般子群。Abel群的任意子群都是不变子群，因为，若G是Abel群，则对于群中的任意a和任意g，都有 $gag^{-1} = gg^{-1}a = a$ 。但是，非Abel群的子群未必就是不变子群。例如，例如，在对称群 $S_3$ 的子群中,根据其常规表达(2.2.7)，2阶循环子群 <y> 就不是不变子群，因为 y在G中，但 $xyx^{-1}$ 不在 <y> 中。

$\bullet$ 一个群G的中心(center)(通常用符号Z表示)是位于G中并可与G的每一个元素可交换(commute)的元素的集合(译注：包括这个可(乘法)交换的元素自身)：

(2.5.12) Z = { z∈G | 对于所有 x∈G 有 xz = zx }。

它总是G的一般子群。特殊线性群 $SL_n(\mathbb{R})$ 的中心包括两个矩阵 $I$ 和 $I^{-1}$ ,对称群 $S_n$ 的中心当 n ≥ 3 时是平凡群。

例子 2.5.13 对称群之间的同态 $\varphi :S_4 \longrightarrow S_3$ 。

有3种方法可以将四个索引的集合{1, 2, 3, 4}划分为二阶子集对，即

(2.5.14) $\Pi_1:\{1,3\}\cup \{3,4\},\Pi_2 : \{1,3\}\cup\{2,4\},\Pi_3 : \{1,4\}\cup\{2,3\}$ 。

对称群 $S_4$ 的一个元素置换(permutes)四个索引,按照这样的方式，置换这3个划分。这定义了从 $S_4$ 到集合 $\{ \Pi_1 ,\Pi_2 ,\Pi_3 \}$ 的置换群(即，对称群 $S_3$ ) 的映射 φ 。例如，4循环p = (1234) 作用在二阶子集上表现如下：

{1，2} $\rightsquigarrow$ {2，3} {1，3} $\rightsquigarrow$ {2，4} {1，4} $\rightsquigarrow$ {1，2}

{2，3} $\rightsquigarrow$ {3，4} {2，4} $\rightsquigarrow$ {1，3} {3，4} $\rightsquigarrow$ {1，4} 。

观察这个动作，我们可以看到 p 作用在划分集合 $\{ \Pi_1 ,\Pi_2 ,\Pi_3 \}$ 上，作为固定 $\Pi_{2}$ 并将 $\Pi_{1}$ 和 $\Pi_{3}$ 交换的转置(transposition) ( $\Pi_1\Pi_3$ )。

假如 p 和 q 是 $S_4$ 的元素，乘积pq是合成置换 p ∘ q ，并且pq在集合 $\{ \Pi_1 ,\Pi_2 ,\Pi_3 \}$ 上的行为是p和q的行为的合成。因此，φ(pq) = φ(p)φ(q),故φ 是一个同态。

这个映射是满射的(surjective)，因此，其像是整个群 $S_3$ 。可以计算出其核。其核是 $S_4$

的子群，由幺元和3个不相交转置的乘积构成：

(2.5.15) K = {1,(12)(34), (13)(24), (14)(23)}。

2.6 同构(ISOMORPHISMS)

(译注：isomorphism[ˌaɪsəʊˈmɔːfɪzəm],来源于 iso- + morphe , iso-词义为“equal, similar, identical; isometric(等于，相似，等同，等距)”，而morphe 词义为“form, appearance(形式，呈现)”，据称这个词由德国化学家Eilhard Mitscherlich (1794-1863)所造。这里主要强调其相同之处。)

一个同构(isomorphism) φ ：G ⟶ G’，是一个从群G到群G’的双射(bijective)的群同态，这个双射使得对于G中的任意两个元素a和b，都有φ(ab) = φ(a) φ(b) 。

例子 2.6.1：

$\bullet$ 对于指数映射 $e^{x}$ ,当其被视为一个从加法群 $\mathbb{R}^{+}$ 到其像(正实数的乘法群)的映射时，它是一个同构。

$\bullet$ 若 a是群G中的一个无限阶元素，发送 $n \rightsquigarrow a^{n}$ 的映射是一个从加法群 $\mathbb{Z}^{+}$ 到G 生的无限循环子群 < a > 的同构。

$\bullet$ n ×n 置换矩阵的子集 𝒫 是 $GL_{n}$ 的一个子集，映射 $S_{n}\longrightarrow \mathcal{P}$ 是一个同构，它将一个置换发送到其关联矩阵(1.5.7)。

引理2.5.9 给了我们一种验证同态φ ：G ⟶ G’是一个同构的方式。我们使用这种方法验证 ker φ = 1 ，这意味着φ 是单射的(injective)，并且 im φ = G’也是单射的，即，φ是满射的(surjective)。

引理 2.6.2 假如 φ ：G ⟶ G’ 是一个同构，则其逆映射 $\varphi^{-1} :G' \longrightarrow G$ 也是一个同构。

证明：

一个单射的逆是一个单射。我们必须证明，对于 G’中的所有 x 和 y , $\varphi^{-1}(x)\varphi^{-1}(y) = \varphi^{-1}(xy)$ 。我们设 $a = \varphi^{-1}(x),b = \varphi^{-1}(y)$ ,且 $c = \varphi^{-1}(xy)$ 。必须证明 ab = c ，且因为φ是双射，这足以证明φ(ab) = φ(c)。因为 φ是一个同态，所以φ(ab) = φ(a) φ(b) = xy = φ(c) 。

这个引理表明，当φ ：G ⟶ G’是一个同构的时候，我们可以在任意一个群中进行计算。然后使用 φ 或 $\varphi^{-1}$ 将其计算结果交给另一个群。因此，根据群定律计算，这两个群具有等同的属性。为了直观地描述这个结论，假设群之一的元素被放进了没有标签的盒子，并且，当用两个盒子表示的时候，有一个预言机(oracle)告诉我们，哪个盒子包含了它们的乘积。我们没有办法决定盒子中的元素是来自G还是来自G’。

对于两个群 G和G’，假如存在一个从 G 到 G’的同构φ ，则称这两个群是同构的。有时候，我们用符号 ≈ 来表示两个群是同构的，即

(2.6.3) G ≈ G’表示 G与G’是同构的。

因为同构的群具有等同的属性，当非正式地提及的时候，通常便于互相验证。例如，我们通常模糊对称群 $S_{n}$ 和置换矩阵的同构群 𝒫 之间的界线。

$\bullet$ 一个已知群G的同构构成所谓的G的同构类(isomorphism class)。

同构类中的任意两个群是同构的。当人们谈及分类群(classifying groups)的时候，其所指的是描述这些同构的类。对于所有群而言，要做分类太难了，但我们将会看到，每个素数阶 p 的群都是循环群。阶数为p的所有群都是同构的。阶数为4的群(2.11.5)有2个同构类，阶数为12的群(7.8.1)的群有5个同构类。

关于同构的一个有趣而有时又容易混淆的点是，存在一个群G到其自身的同构φ ： G ⟶ G。我们称这样的同构为自同构(automorphism)。显然，恒等映射是一个自同构，但几乎总是有其它自同构。最重要的自同构类型是共轭：令 g 为 G 中的固定元素。按g的共轭是从G到其自身的映射 φ ，定义为

(2.6.4) $\varphi(x) = gxg^{-1}$ 。

这是一个自同构，原因在于，首先，它是一个同态：

$\varphi(xy) = gxyg^{-1} = gxg^{-1} gyg^{-1} = \varphi(x)\varphi(y)$ (译注： $y = gg^{-1}y = gyg^{-1}$ ), 第二，它是双射的，因为它有逆函数——按 $g^{-1}$ 的共轭。

若群是Abel群，按任意元素 g 的共轭是恒等映射： $gxg^{-1}=x$ 。但是，任意非可交换群具有非平凡共轭，因此，它具有不同于恒等映射的自同构。例如，对称群 $S_3$ ，按通常的表示，按 y 的共轭是交换 $x$ 和 $x^{2}$ 。

如前所述，元素 $gxg^{-1}$ 是 x 按 g 的共轭，而对于群 G 的两个元素 x 和 x’ ，若对于 G 中的某个g 有 $x' = gxg^{-1}$ ，则称这两个元素是互为共轭的。共轭 $gxg^{-1}$ 表现出来的行为与元素x自身高度一致；例如，在群中具有相同的阶数。这一点可以通过它是按自同构的x的像这一事实推导出来。(参见引理2.6.2的讨论。)

注意：有时候，人们可能希望确定群 G 的两个元素 x 和 y 是否是共轭的，即，是否存在G中的一个元素 g，使得 $y=gxg^{-1}$ 。将 g 的求解方程重写为 yg = gx 几乎总是更简单。

$\bullet$ 交换子(commutator) $aba^{-1} b^{-1}$ 是与一个群的一个元素对 a，b 关联的另一个元素。

下面的引理可以通过将方程的一侧的元素移到另一侧的方式推导出来。

引理 2.6.5 对于群的两个元素a和 b ，当且仅当 $aba^{-1}=b$ 且当且仅当 $aba^{-1}b^{-1}=1$ 1 时其成立，则群的这两个元素(乘法)可交换，即，ab = ba。

2.7 等价关系和划分(EQUIVALENCE RELATIONS AND PARTITIONS)

等价关系是一种基本的数学构造，它从集合 S 开始，并通过使 S 的某些元素“等价(equating)”来形成新的集合。例如，我们可以将整数集合分成两类，偶数整数和奇数整数。我们所获得的新集合由两个元素构成，这两个元素可以分别统称为偶数元素(Even)和奇数元素(Odd)。或者，通常将平面中的全等三角形(congruent triangles)视为等价的几何对象。这种非常一般化的过程(procedure)可以由几种方式引发，我们接下来就来讨论它们。

$\bullet$ 一个集合S的一种划分(partition) Π 是一种将S分割成非重叠的、非空的子集的一种细分(subdivision)：

(2.7.1) S = 不相交非空子集的并集。

奇偶集这两个集合是整数集的一个划分。根据常规记法，集合

(2.7.2) {1} ， $\{ y, xy,x^{2} y \}$ , $\{ x, x^{2} \}$

构成对称群 $S_3$ 的一种划分。

$\bullet$ 一个集合S上的一种等价关系(equivalence relation)是一种在S的某些元素对之间成立的一种关系。我们可以将其写为 a ~ b 并读作“a 与 b的等价关系”。一种等价关系要求具有如下特性：

(2.7.2)

$\bullet$ 传递性(transitive): 若 a ~ b ，b ~ c , 则 a ~ c 。

$\bullet$ 对称性(symmetric): 若 a ~ b ，则 b ~ a 。

$\bullet$ 自反性(reflexive): 对于所有的 a ，有 a ~ a 。

三角形全等(congruent)是平面中三角形集合的等价关系的一个例子。若 A，B和C是三角形，并且 A 全等于B，并且 B 又全等于C，则 A全等于 C，等等。

共轭是群上的一种等价关系。两个群的元素互为共轭，若对于群的某个元素 g， $b=gag^{-1}$ , 则 a ~ b 。我们验证传递性：假设 a ~ b 和b ~ c 。这意味着，对于某些群的元素 $g_{1}$ 和 $g_{2}$ , 有 $b = g_{1}ag_{1}^{-1}$ ， $c = g_{2}bg_{2}^{-1}$ 。则， $c = g_{2}bg_{2}^{-1} = g_{2}(g_{1}ag_{1}^{-1})g_{2}^{-1}=(g_{2}g_{1})a(g_{1}g_{2})^{-1}$ ，因此，a ~ c 。

关于S的划分和S的等价关系的概念是逻辑上的等价，尽管在实践中可能只用两者之一来表示。

命题 2.7.4 一个集合 S 上的一种等价关系确定了S的一种划分，反之亦然。

证明：

已知S的一个划分，定义这个对应的等价关系的规则是，若a和b位于划分的同一个子集中，则a ~ b 。很明显，满足等价关系的公理。反之，已经一个等价关系，定义划分的方式为：包含a的子集是使得 a ~ b 的所有的元素b 的集合。称这个子集为a的等价类。在这里，我们将用符号 $C_{a}$ 来表示：

(2.7.5) $C_a=\{ b \in S| a \sim b \}$ 。

下面的引理完成了对本命题的证明。

引理 2.7.6 已经一个集合S上的一种等价关系，作为等价类的S的子集划分S。

证明：

这是一个重要的点。因此我们将存细验证。我们必须牢记，符号 $C_a$

示按某种方式定义的子集。划分由子集构成，并且有几个符号可以描述同样的子集。

自反性定理告诉我们，a位于其等价类中。因此，类 $C_a$ 是非空的，且因为a可以是任意元素，等价类的并集是整个集合S 。余下的必须验证的划分属性是等价类是不相交的。为了证明这一点，我们证明：

(2.7.7) 若 $C_a$ 和 $C_b$ 具有一个共同元素，则 $C_a=C_b$ 。因为我们可以交换 a 和 b的角色，这足以证明，若 $C_a$ 和 $C_b$ 具有一个共同元素，比如说 d，则 $C_b \subset C_a$ ，即， $C_b$ 的任意元素 x 也在 $C_a$ 中。若 x 在 $C_b$ 中，，则 b ~ x 。因为 d同时在两个集合中，则 a~ d和b ~ d ，并且 b ~ x 。应用两个传递性证明 a ~ x ，因此，x 在 $C_a$ 中。

例如，若a和b是同阶元素，则由 a~ b所定义的群上的关系是一种等价关系。对于对称群 $S_3$ ，对应的划分展示在(2.7.2)中。

若已知一个集合S 的一个划分，我们可以构造一个新的集合 $\overline{S}$ ，其元素是子集。我们可以想象成，将子集放入单独的堆里面(piles),我们将这些堆视为我们新构造的集合 $\overline{S}$ 的元素。似乎建议使用一种符号来区分子集和它所表示的集合 $\overline{S}$ 堆)的元素。若 U是一个子集，我们将使用[ U ] 来表示对应的 $\overline{S}$ 的元素。因此，若 S 是整数集，且若分别使用偶元素集(Even)和奇元素集(Odd)来表示偶数和奇数整数集，则 $\overline{S}$ 包含两个元素 [Even] 和 [Odd] 。

我们将使用更通用的记法。当我们希望将 S的子集U 视为一个 S的子集的集合的元素，我们使用符号 [ U ] 来表示。

当已知 S 上的等价关系时，等价类形成一个划分，我们得到一个新的集合 $\overline{S}$ ，其元素是等价类 $[C_{a}]$ ，我们可以按另一种方式，将这个新集合的元素视为通过改变元素之间等价的含义而获得的集合。如果a和b在S中，我们将a ~ b 解释为 a 和 b 在 $\overline{S}$ 中等价，因为 $C_a=C_b$ 。从这种角度来看，两个集合 $S$ 和 $\overline{S}$ 之间的区别在于，S 中更多的元素被声明为“相等”，即等价。在我看来，我们在学校里经常这样对待全等三角形。

对于任意等价关系，存在一个自然的满射

(2.7.8) $\Pi: S \longrightarrow \overline{S}$ ,

它将S的元素a , 映射到其等价类： $\Pi (a) = [C_a]$ 。当我们希望将 $\overline{S}$ 视为通过改变等价的概念从S获得的集合时，用符号 $\overline{a}$ 来表示 $\overline{S}$ 的元素 $[C_a]$ 会带来便利。则映射π 成了

$\pi (a) = \overline{a}$ 。

我们在 $\overline{S}$ 中工作时可以使用用于 S 的元素的符号，但是，使用上划线来提醒我们使用的是新的法则：

(2.7.9) 若 a 和 b 在S 中，则 $\overline{a}=\overline{b}$ 意味着 a ~ b 。

上划线符号的一个缺陷在于，多个符号表示 $\overline{S}$ 的同一个元素。有时候，可以通过在每一个等价类中选取特定的元素(一个代表元素)来表示，从而克服这种缺陷。例如，偶整数元素和奇整数元素通常分别使用 $\overline{0}$ 和 $\overline{1}$ 来代表：

(2.7.10) $\{[Even],[Odd] \}=\{ \overline{0},\overline{1} \}$ 。

起初，尽管堆图可能更容易掌握，但是将其视为 S 的这第二种方式通常更好，因为上划线记法使用代数方法更容易操控。

2.7.1 由映射定义的等价关系(The Equivalence Relation Defined by a Map)

集合的任何映射 f：S ⟶ T 给到我们一个基于其域 S 之上的一种等价关系。若 f (a) = f (b) ，则这种等价关系由法则 a ~ b所定义。

$\bullet$ T 的一个元素 t 的逆像(inverse image)是S 的子集，它由S中使得 f (s) = t 的所有 s 元素所构成。用符号表示为

(2.7.11) $f^{-1}(t) = \{ s\in S| f (s) = t \}$ 。

这是符号的记法。请牢记，若非f 是双身， $f^{-1}$ 不能成为映射。这个逆像也被称为映射f的纤维(fibres)，并且，不为空的纤维是按如上所定义关系的等价类。

在这里，等价类的集合 $\overline{S}$ 有另一个化身(incarnation),作为映射的像，像的元素按双射对应非空纤维(即，等价类)。

(2.7.12) 绝对值映射 $\mathbb{C}^{\times} \longrightarrow \mathbb{R}^{\times}$ 的某些纤维。

我们回到群同态φ ：G ⟶ G’。通过φ 在G上定义的等价关系通常用符号“≡”表示,而不是使用符号 ~ ，并且称为同余(congruence)：

(2.7.13) a ≡ b (若 φ(a) = φ(b))。

我们已经看到，G的元素a和b 是同余的，即，当且仅当b位于核 K (2.5.8)的陪集 aK中时，φ(a) = φ(b) 。

命题 2.7.15 令 K 为一个同态 φ ：G ⟶ G’ 的核。包含G的一个元素 a的φ的纤维是K的陪集aK。这些陪集划分了群G ，并且，它们对应φ的像的元素。

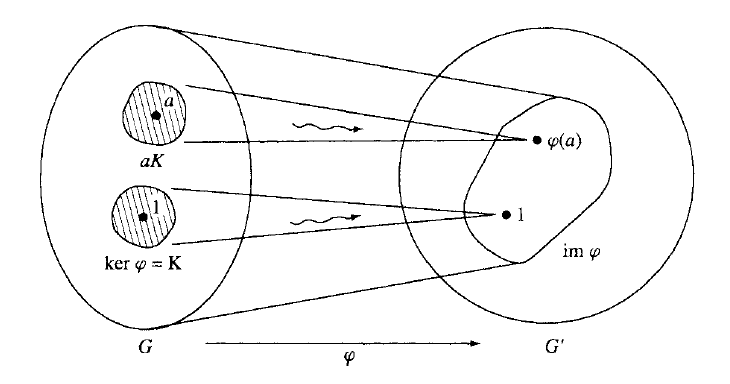
(2.7.16) 一个群同态的示意图。

2.8 陪集(COSETS)

如前所述，若H是 G 的一个子集且若a是G的一个元素，则子集

(2.8.1) aH = { ah | h在G中 }

被称为一个左陪集(a left coset)。子群H是一个特殊的左陪集，因为 H = 1H 。

G 中H 的陪集是同余关系的等价类

(2.8.2) a ≡ b (若对于某个H中的 h ，b = ah )。

这非常简单，但让我们来验证同余关系是一个等价类。

传递性：假如 a ≡ b 和 b ≡ c 。这意味着，对于H中的某两个元素h和h’ ，有 b = ah ，c = bh’ 。因此，c = ahh’ 。因为H是一个子群，hh’ 在H中，因此，a ≡ c。

对称性：假如 a ≡ b，因此，b ≡ ah。则 $a \equiv bh^{-1}$ 且 $h^{-1}$ 在H 中，因此，b ≡ a 。

自反性：a ≡ a1 且 1 在H 中，因此，a ≡ a 。

注意，在这里，我们已经利用了所有定义子群的属性：闭合，幺元，和逆元。

引理 2.8.3 一个群G的一个子群H的左陪集划分了这个群。

证明：

左陪集是同余关系(2.8.2)的等价类。

牢记——记法 aH 定义了G的某个子集。与任何等价关系一样，几种符号可以定义同一个子集。例如，在对称群 $S_3$

中，按照常规表示(2.2.6) , 元素 y生成一个2 阶循环子群 H = < y > 。在 G 中，有3个H 的陪集：

(2.8.4) $H = \{1 ,y \} = yH$ ， $xH = \{x ,xy \} = xyH$ ， $x^{2}H = \{ x^{2} ,x^{2}y \} = x^{2}yH$ 。

这些子集确实分割了群。

综上所述，令 H 为G的子集，并令 a和b 为G的元素。下面的3种表述是等价的：

(2.8.5)

$\bullet$ 对于H 中的某个h , 有 b = ah ，或 $a^{-1}b$ 是 H 的元素；

$\bullet$ b是左陪集 aH 的一个元素；

$\bullet$ 左陪集ah和bh是相等的。

一个子群的左陪集的数量被称为 G 中H 的索引(index)。这个索引表示为

(2.8.6) [G : H ] 。

因此， $S_3$ 的子群 < y > 的索引是 3 。当G是无限的时候，这个索引也是无限的。

引理 2.8.7 一个群G 的一个子集H的所有左陪集具有同样的阶数。

证明：

用a相乘定义一个映射 H ⟶ aH ，这个映射发送 h ⇝ ah 。这个映射是双射，因为其逆元是使用 $a^{-1}$ 的乘法。

因为所有左陪集都具有相同的阶数，且因为它们划分这个群，所以，我们获得了重要的阶数的计算公式(Counting Formula)

(2.8.8) |G| = |H || G:H |

(G的阶数) = (H的阶数)(左陪集的数量)，

其中，一如往常，|G|表示群的阶。如果某些项是无限的，则等式具有明显的意义。对于 $S_3$ 的子群 < y > ，这个公式读作 6 = 2 • 3 。

从这个计算公式可以推导出，(2.8.8)的右边的项整除左边的项。这些事实之一被称为Lagrange定理。

定理 2.8.9 Lagrange定理令H为一个有限群G的一个子群。则H的阶数整除G的阶数。

引理 2.8.10 一个有限群的一个元素的阶数整数这个群的阶数。

证明：

一个群G的一个元素a的阶数等于由a所生成的循环子群< a >的阶数(命题2.4.2)。

引理 2.8.11 假如一个群G具有素数阶数p 。令 a 为 G 的幺元之外的任意元素。则 G 是由 a 所生成的循环群。

证明：

一个元素 a ≠ 1 的阶数大于1，并且其阶数整除G的阶(素数阶p)。因此，a的阶数等于p。这也是由a所生成的循环子群 < a > 的阶数。因为 G具有阶数 p , < a > = G 。

这个引理对素数阶数p进行了分类。它们构成了一个同构的分类—— p 阶循环群类。

当已知一个同态φ ：G ⟶ G’的时候，也可以应用这个阶数的计算公式。正如(2.7.15)所示，核 ker φ 的左陪集是映射φ的非空纤维。它们以双射与像的元素对应。

(2.8.12) | G: ker φ| = |im φ| 。

引理 2.8.13 令 φ ：G ⟶ G’为一个有限群的同构。则

$\bullet$ | G: ker φ| = | ker φ||im φ|；

$\bullet$ | ker φ|整除| G |且

$\bullet$ | im φ|整除 | G | 和 | G’ |两者。

证明：

第一个公式可以结合 (2.8.8) 和 (2.8.8) 获得，意味着 | ker φ|和|im φ|整除 | G | 。因为像是G’ 的一个子群。Lagrange定理告诉我们，它的阶数也整除| G’ | 。

例如，符号同态 $\sigma:S_n \longrightarrow \{\pm1\}$ (2.5.2)(b)是满射，因此，它的像具有阶数2 。其核(交替群 $A_{n}$ ) 具有阶数 $\frac{1}{2}n!$ 。 $S_{n}$ 的一半元素是偶置换，另一半元素是奇置换。

当已知子群的链(chain)的时候,计算公式 2.8.8具有一个类比。

命题 2.8.14 素引的乘法属性。令 G ⊃ H ⊃ K 为一个群G的子集。则 [G: K ] = [G: H ][H: K ] 。

证明：

我们假设右边的两个索引是有限的，比如说，[G: H ] = m，[H: K ] = n。当一个或另一个是无限的情况下，推理类似。我们列出G中H的陪集m 。对每一个陪集，选取代表元素，比如， $g_{1}H ,...,g_{m}H$ 。则 $g_{1}H \cup ... \cup g_{m}H$ 是G的一个划分。类似地，我们选择取H中K的陪集的每一个代表元素，获得一个划分 $H = h_{1}K ,... ,h_{n}K$ 。因为按 $g_i$ 的乘法是逆运算， $g_{i}H = g_{i} h_{i}K ,... ,g_{i} h_{n}K$ 将是陪集 $g_{i}H$ 的一个划分。将这些划分放到一起，G 被划分成一个 mn 陪集 $g_{i}h_{i}K$ 。

2.8.1 右陪集(Right Cosets)

让我们回到陪集的定义。我们决定使用左陪集 aH。人们也可以定义一个子群H的右陪集，并重复上述论述。一个群G的子群H是集合

(2.8.15) Ha = { ha | h∈G } 。

它们是关系(右同余)的等价类

a ≡ b (若对于某个H中的 h ，b = ha )。

右陪集也划分群 G ，但是它并非都和左陪集一样划分。例如， $S_{3}$ 的子群 < y > 的右陪集是

(2.8.16) $H = \{1 ,y \} = Hy$ , $Hx = \{ x ,x^{2}y \} = Hx^{2}y$ , $Hx^2 = \{ x^{2} ,xy \} = Hxy$ 。

这与划分(2.8.4)的左陪集是不同的。然而，如果一个子群是常规的，其左陪集和右陪集是相同的。

命题 2.8.17 令 H 为群G的子群。下面的3种表述是等价的：

(i) H 是一个不变子群：对于H中的所有h 和 G中的所有g ,有 $g^{-1}hg$ 在H 中。

(ii) 对于 G 中的所有 g ,有 $g^{-1}hg=H$ 。

(iii) 对于 G中的所有g ,左陪集 gH 等于右陪集 Hg 。

(iv) G中H的每一个左陪集都是一个右陪集。

证明：

假设H 是一个不变子群。因此，(i) 成立，它意味着对于G 中的所有g ，有 $gHg^{-1} \subset H$ 。替换 $g^{-1}$ 为 g 证明 $g^{-1} Hg\subset H$ 也成立。我们在这个包含式(inclusion)的左边乘以g，右边乘以 $g^{-1}$ ，从而推导出 $H \subset gHg^{-1}$ 。因此，必然有 $g^{-1} Hg= H$ 。这证明了 (i) 并意味着(ii)。很明显，(ii) 意味着 (i)。接下来，若 $gHg^{-1} = H$ ，我们在这个等式的右边乘以g，并推导出 gH = Hg 。这就推导出了(ii)并意味着(iii)。也可以看到，类似地，有(iii)意味着(ii)。因为(iii)意味着(iv)很明显，就只乘下(iv) 意味着(iii)的证明。

我们问：在什么场景下，一个左陪集等于一个右陪集？我们想到，左陪集划分群 G ，并注意到，左陪集 gH 和右陪集Hg有一个共同元素，即，g = g.1 = 1. g 。因此，若左陪集gH等于任何右陪集的话，这个右陪集一定是Hg。

命题 2.8.18

(a) 若H是 G 的一个子集且若a是G的一个元素，则集合 $g^{-1} Hg$ 也是一个子群。

(b) 若一个群G仅有一个r阶子群H，则子群是不变子群。

证明：

(a) 按g的共轭是G的一个自同构(automorphism)(见(2.6.4))，且 $gHg^{-1}$ 是H 的像。(b)见(2.8.17): $gHg^{-1}$ 是一个r 阶子群。

注意：若H是一个有限群 G 的一个子群，用于左右陪集的计算公式是相同的，因此，左右陪集的数量相同。当G 是一个无限群的时候，虽然没有使用计算来证明，但是这条规则依然成立(见练习M.8)。

2.9 模数运算(MODULAR ARITHMETIC)

本节简要讨论数论中最重要的概念之一：整数同余。如果您以前没有遇到过这个概念，您将需要相关内容。例如，参见[Stark]。在整个部分中，我们使用固定的正整数 n。

对于两个整数 a和 b，如果对于某个整数 k，n 整除b – a ，或者 b = a + nk ，则称其模n 同余(以n为模同余),记作

(2.9.1) a ≡ b modulo n 。(译注：读作“a和b模n同余”,或简记为 a ≡ b mod n。)

例如，2 ≡ 17 modulo 5 。

容易验证，同余是一种等价关系，因经，我们可以考虑它所定义的等价类，称为同余类。我们使用上划线记法，并使用符号 $\overline{a}$ 表示一个整数 a 模n的同余类。这个同余类是整数的集合，即

(2.9.2) $\overline{a} = \{...,a - n , n ,a + n ,a + 2n,...\}$ 。

若 a和 b 是整数， $\overline{a}=\overline{b}$ 意味着 a ≡ b modulo n ，或者 n整除b – a 。同余类 $\overline{0}$ 是整数加法群 $\mathbb{Z}^{+}$ 的子群

$\overline{0}=\mathbb{Z}n = \{...,-n , 0 ,n , 2n ,...\} = \{ kn | k \in\mathbb{Z} \}$ 。

其它的同余类是子群的陪集。请注意，ℤn不是右陪集，它是整数加法群 $\mathbb{Z}^{+}$ 的子群。一个子群H的陪集符号类似于aH，但是，使用合成律的加法记法是 a + H = { a + h | h∈H } 。为了简化记法，我们用来H表示子群 ℤn ，则H的陪集(同余类)是

(2.9.3) a + H = { a + kn ，k∈ℤ } 。

n个整数 0 ,1, ... , n – 1 是n同余类的代表元素。

命题 2.9.4 存在 n 个模 n 同余类，即 $\overline{0}$ , $\overline{1}$ , ... , $\overline{n-1}$ 。ℤ 中子群 ℤn 的索引[ℤ: ℤn]的索引是n。

令 $\overline{a}$ 和 $\overline{b}$ 为用整数 a和 b所表示的同余类。定义它们的和为 a + b 的同余类，并定义它们的积为 ab类。换句话说，根据定义，有(2.9.5)

$\overline{a}+\overline{b}=\overline{a+b}$ 和 $\overline{a}\overline{b}=\overline{ab}$ 。

对这个定义，需要作一些解释。因为同一个同余类可以使用很多不同的整数表示。任何模n同余a的整数a’都表示用a表示的同一个类。所以，最好是这样，若 a’≡ a ，b’≡ b ，则 a’+ b’ ≡ a + b 模n和 a’b’ ≡ ab 模n。幸运的是，的确是这样。

引理 2.9.6 若 a’≡ a模n，b’≡ b模n，则 a’+ b’ ≡ a + b 模n和 a’b’ ≡ ab 模n。

证明：

假设 a’≡ a 和 b’≡ b ，因此，对于某两个整数 r和 s，a’= a + rn , b’= b + sn 。则 a’+ b’ = a + b + (s + r )n 。这就证明了 a’+ b’ ≡ a + b 。类似地，a’b’= (a + rn)(b + sn) = ab + (as + rb + rns)n ，a’b’ ≡ ab 。

对于同余类的加法和乘法，结合律，交换律和分配律成立，因为它们对于整数的加法乘法成立。例如，对分配律的验证如下：

$\overline{a}(\overline{b}+\overline{c})=\overline{a}(\overline{b+c})=\overline{a(b+c)}$ (根据同余类的+和×的定义)

------------------------------- $= \overline{ab+ac}$ (根据整数分配律)

------------------------------- $= \overline{ab} + \overline{ac} = \overline{a}\overline{b} + \overline{a} \hspace{0.1cm}\overline{c}$ (根据同余类的+和×的定义)。

其它定律的验证类似，我们这里不再验证。

同余类模n的结合可以使用符号 ℤ/ ℤn，ℤ/ nℤ ，或 ℤ /(n) 中任一个表示。ℤ/ ℤn中加，减，和乘可以使用整数显式实现，并使用n相除后取得余数。这就是公式(2.9.5)的含义。它们表明了映射

(2.9.7) ℤ ⟶ ℤn ，

这个将整数a发送到其同余类的映射与加法和乘法是兼容的。因此，可以在整数中完成计算，最后将结果搬运到ℤn 。但是，如果数较小，则计算更简单。在计算的某些部分完成后，可通过计算余数实现。

因此，若 n = 29,那么 $\mathbb{Z}n =\{\overline{0} ,\overline{1},\overline{2}, ... \overline{28}\}$ ，则 $(\overline{35})(\overline{17}+\overline{7})$ 可计算为 $(\overline{35})(\overline{24})=(\overline{6})(\overline{-5})=-\overline{30}=-\overline{1}$ 。

从长远来看，数字上划线表示法是显得麻烦(nuisance)，通常忽略上划线。当略去上划线后，人们仅需记住这个规则：

(2.9.8) 在ℤ/ ℤn 中称 a = b ，指的就是 a ≡ b modulo n 。

模一个素数整数的同余具有特别的属性，我们将在下一章的开头部分讨论。

2.10 关于满射同态群的对应定理(THE CORRESPONDENCE THEOREM)

令φ ：G ⟶ 𝒢 (译注：LaTex语法“mathcal{G}”,Unicode:U+ 1D4A2) 为一个同态群，并令 H为 G 的一个子群。我们可以将φ限定在 H ，从而获得一个同态

(2.10.1) $\varphi |_{H}:H \rightarrow \mathcal{G}$ 。

这意味着，我们采用相同的映射但限定了其作用域：因此，根据定义，若h在H中，则 $[\varphi |_{H}](h)=\varphi(h)$ 。(为清晰起见，我们在符号 $\varphi |_{H}$ 外层加了方括号。) 加了限定后还是一个同态，因为φ是一个,而 $[\varphi |_{H}]$ 的核是φ的核与H的交集：

(2.10.2) $\ker(\varphi |_{H})= \ker(\varphi )\cap H$ 。

根据核的定义，这是显然易见的。 $[\varphi |_{H}]$ 的像与映射φ下的H像φ(H )是相同的。

计算方法可能有助于描述这种限定。根据引理(2.8.13),像的阶数整除| H |和| 𝒢 |。若 | H |和| 𝒢 |没有公因子，φ(H ) = {1} ，因此，H 包含于核中。

例子 2.10.3 符号同态 $\sigma:S_n \rightarrow \{\pm 1\}$ 的阶数为2 。若对称群 $S_n$ 的一个子群具有奇数阶数，则它将包含于 σ 的核(偶置换的交替群 $A_{n}$ )中。当H是由一个置换q(群中一个奇数阶数的元素)所生成的循环子群的时候，也是如此。群中的阶数为奇数的每一个置换(例如，具有n阶的奇置换n-cycle)都是一个偶置换。在群中，具有偶数阶数的置换可能是奇置换或偶置换。

命题 2.10.4 令φ ：G ⟶ 𝒢 为一个核为K 的同态，并令ℋ 为 𝒢 的一个子群。用 H 表示逆像 $\varphi^{-1}(\mathcal{H})$ 。则H是G的含有K的子群。若 ℋ 是 𝒢 的一个不变子群，则H是G的一个不变子群。若φ是满射，并且若H是G的一个不变子群，则ℋ 是 𝒢 的一个不变子群。

例如，令 φ 表示行列式同态 $GL_{n}(\mathbb{R}) \rightarrow \mathbb{R}^{\times}$ 。则正实数的集合是 $\mathbb{R}^{\times}$ 的一个子群；通常是因为 $\mathbb{R}^{\times}$ 是一个Abel群。其逆像(具有正行列式的逆矩阵的集合)是 $GL_{n}(\mathbb{R})$ 的一个不变子群。

证明：

证明很简单，但是我们必须谨记 $\varphi^{-1}$ 不是一个映射。根据定义， $\varphi^{-1}(\mathcal{H} ) = H$ 是使得φ(x)在ℋ中的G的元素x的集合。首先，若 x 在核 K中，则φ(x) = 1 。因为 1 在 ℋ中，所以x在H中。因此，H 包含K 。下面我们逐条验证子群的条件。

闭合性：假设 x和y在H中。则φ(x)和φ(y)在ℋ中。因为ℋ是一个子群，φ(x)φ(y)在ℋ中。因为φ是一个同态，φ(x)φ(y) = φ(xy)。因为φ(xy)在ℋ中，则xy在H 中。

幺元：1 在H 中，因为 φ(1) = 1 在ℋ中。

逆元：令x为H 的一个元素。则φ(x) 在ℋ 中 ,因为 ℋ是一个子群，因此 $\varphi(x)^{-1}$ 也在ℋ 中。因为φ是一个同态，则 $\varphi(x)^{-1} = \varphi(x^{-1})$ ，因此 $\varphi(x^{-1})$ 也在ℋ中,并且 xy 在H 中。假设ℋ是一个不变子群。分 x 和 g 分别为H 和G 的元素。则 $\varphi(gxg^{-1}) = \varphi(g) \varphi(x)\varphi(g)^{-1}$ 是φ(x)的一个共轭，且φ(x)在ℋ中。因为是ℋ不变的，故 $\varphi(gxg^{-1})$ 在ℋ中,因此有 $gxg^{-1}$ 在H 中。

假如φ是一个满射，且 H 是G的一个不变子群。令 a 为 ℋ中的一个元素且令b 为 𝒢 中的一个元素。则存在H 中的元素 x 和 G 中的元素 y，使得 φ(x) = a , φ(y) = b 。因为是H 不变子群， $yxy^{-1}$ 在H 中，因此， $\varphi(yxy^{-1}) = bab^{-1}$ 在 ℋ 中。

定理 2.10.5 对应定理(Correspondence Theorem)。

令 φ ：G ⟶ 𝒢 为一个核为K的满射群同态。则在 𝒢 的子群和G的含有K的子群之间存在一种双射对应关系：

{G的含有K的子群} ⟷ {G的子群}。

这种定义关系定义如下：

G的含有K的子群H ⇝ 其像 φ(H )在 𝒢 中，

𝒢 的一个子集 ℋ ⇝ 其逆像 $\varphi^{-1}(\mathcal{H})$ 在G中。

若 H 和 ℋ 是对应的子群，则当且仅当 ℋ 在 𝒢 中是不变子群的时候，H 在G中是不变子群。若 H 和 ℋ 是对应的子群，则 | H | = |ℋ||K|。

例子 2.10.6 我们回到例子2.5.13中定义的同态 $\varphi:S_{4} \rightarrow S_{3}$ 以及其核 K (2.5.15)。

群 $S_{3}$ 有6个子群，其中有4个是真子群(proper subgroups)。根据惯常的表示方法，有一个是3阶真子群(循环群< x >)，以及三个2阶子群(包括< y >)。对应定理告诉我们，存在4个 $S_{4}$ 的包含K 的真子群。因为 |K| = 4 ，所以，存在一个12阶的子群和四个8阶的子群。

我们还知道一个12阶的子群，即交替群 $A_{4}$ 。那是一个对应于 $S_{3}$ 的循环群 < x >。

8阶的子群可以根据一个正方形的对称性来解释。根据如下图中所标的正方形的顶点(vetices),一个通过角1逆时针π/2 角度的旋转对应4循环(1234)。通过顶点 1 的对角线的反射对应于转置 (24) 。这两个置换生成一个8阶子群。其他8阶子群可以通过以其他方式标记顶点来获得。

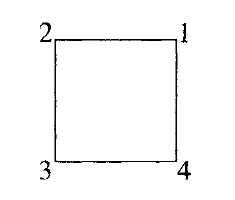
也存在一些 $S_{4}$ 的不包含K的子群。对应定理并没涉及到这些群。

对应定理的证明。

令H为 G 的包含K的一个子群，并令ℋ 为 𝒢 的一个子群。我们必须验证以下要点：

$\bullet$ φ( H ) 是 𝒢 的一个子群。

$\bullet$ $\varphi^{-1}(\mathcal{H})$ 是G的一个包含K 的子群。

$\bullet$ 当且仅当 $\varphi^{-1}(\mathcal{H})$ 是G的一个不变子群的时候，ℋ是 𝒢 的一个不变子群。

$\bullet$ (相应的双射) $\varphi( \varphi^{-1}(\mathcal{H})) = \mathcal{H}$ 且 $\varphi^{-1}(\varphi(H)) = H$ 。

$\bullet$ $|\varphi^{-1}(\mathcal{H})| = | \mathcal{H}||K|$ 。

因为 φ (H )是同态 $\varphi|_{H}$ 的像，因此，它是 𝒢 的一个子群。第二和第三个黑点条目构成了命题 2.10.4。

考虑第四个黑点条目，等式 $\varphi( \varphi^{-1}(\mathcal{H})) = \mathcal{H}$ 对于任意结合的满射 φ ：S ⟶ S’ 和任意 S’ 的子集ℋ 都成立。此外， $H \subset \varphi^{-1}(\varphi(H ))$ 对于任意集合的映射φ和 S 的任意子集 H都成立。我们略去对这些事实的验证。则余下的唯一需要验证的是 $H \supset \varphi^{-1}(\varphi(H ))$ 。令 x 为 $\varphi^{-1}(\varphi(H ))$ 的一个元素。我们必须证明 x 在H 中。根据逆像的定义，φ(x )在φ(H )中，比如说 φ(x ) = φ(a) ，且 a 在H 中。在 $a^{-1}x$ 在核 K中(2.5.8)，并且，因为H 包含 K ， $a^{-1}x$ 在H 中。因为 a 和 $a^{-1}x$

两者都在H中，所以，x 也在H 中。

我们将最后一个黑点项留作证明。

2.11 乘法群(PRODUCT GROUPS)

令 G ，G’ 为2个群。乘积的集合 G×G’ ( 元素对( a , a’)的集合，且 a 在G中，a’在G’ 中)可以按逐分量相乘而被构造成一个群——即，由规则

(2.11.1) (a , a’)•( b , b’) = (ab, a’ b’)

所定义的乘法对。数对(1,1) 是幺元(单位元)，并且 (a , a’)的逆元是 ( $a^{-1}$ , $a'^{-1}$ ) 。G×G’ 中的结合律可以基于在 G 和G’ 中成立的事实推导。

按这种方式所获得的群称为G 和G’ 的乘法群，并记为 G×G’ 。它与两个因子 G 和G’ 相关。根据某些同态

(2.11.2)

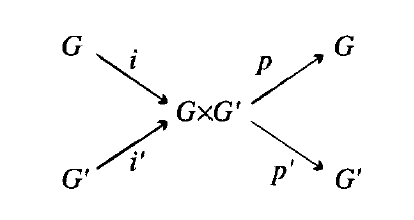
可以以一种简单的方式来概括这种关联。这种方式定义为：i(x) = (x,1), i'(x’) = (1, x’ ),p( x, x’ ) = x ，p’( x, x’ ) = x’ 。单射同态 i 和i' 可以用于识别 G 和 G’ 以及它们的像( G×G’ 的子群 G×1 和 1×G’ )。映射p 和p' 是满射的，p 的核是 1×G’ ，p’ 的核是 G×1 。这些是投影(projections)。

显然，期望将已知群分解为乘积项，即，求得群 H和 H ’ ，使得G对乘积 H×H ’ 是同构的。这样的话，群 H和 H ’ 会更简单，H×H ’ 与其因子的关系更容易被理解。一个群是乘积的情况很少见，但偶尔也会出现。

例如，相当惊奇的是，6阶循环群可以被分解：6阶循环群 $C_{6}$ 与 2阶和3阶循环群的乘积 $C_{2} \times C_{3}$ 是同构的。我们举例说明这一点，比如，设 $C_2 = < y >$ , $C_3 = < z >$ ,且 $y^2 = 1$ 和 $z^3 = 1$ ，并令 x 表示乘积群 $C_{2} \times C_{3}$ 的元素(y , z )。使得 $x^k = ( y^k , z^k )$ 是幺元 (1,1) 的最小正整数是 k = 6 。因此，x的阶是 6 。因为 $C_{2} \times C_{3}$ 的阶也是6，所有，它等于循环群 < x > 。按阶次序，x 的幂是

$(1,1),(y ,z),(1 , z^2),(y ,1),(1 , z),(y ,z^2)$ 。

对于rs 阶循环群，只要这两个整数r和s没有公因子，也存在类似的表述。

命题 2.11.3 令 r 和 s 为相对素数整数。一个 rs 阶循环群与一个r阶循环群和一个s 阶循环群的乘积同构。

在另一方面，4阶循环群与两个2阶循环群的乘积不是同构的。 $C_2 \times C_2$ 的每一个元素都具有1阶或2阶，而一个4阶循环群包含两个4阶元素。

下面的命题描述了乘法群。

命题 2.11.4 令 H和 K为一个群 G的子群,并令 f：H×K⟶ G 为乘法映射，由 f ( h,k ) = hk 所定义。其像是集合 HK = { hk| ，h∈H，k∈K }。

(a) 当且仅当 H∩K = { 1 } 时，f 是单射的。

(b) 当且仅当 K 的元素与H的元素可交换时(即，hk = kh),从乘法群 H×K 到G的映射f 是一个同态。

(d ) 当且仅当 H∩K = { 1 } 且 HK = G 时，从乘法群 H×K 到G的映射f 是一个同态，并且H和 K为一个群 G的不变子群。

注意到这一点很重要——对于乘法映射而言，尽管它不是一个群同构，但它可能是双射的。当 $G = S_3$ 时且根据常规记法 H = < x > 和 K = { y }，就会出现这种情况。

证明：

(a) 若 H∩K 包含一个元素 x ≠ 1 ，则 $x^{-1}$ 在H 中，则 $f ( x^{-1} , x ) = 1 = f (1, 1 )$ ,因此，f 不是单射的。假如 H ∩ K = { 1 }。令 $(h_1, k_1)$ 和 $(h_2, k_2)$ 为使得 $h_{1}k_{1}=h_{2}k_{2}$ 的 H×K 的元素。我们在等式两边的左侧乘以 $h_{1}^{-1}$ ，在等式两边的右侧乘以 $k_{2}^{-1}$ , ，从而得到 $k_1 k_2^{-1} = h_1^{-1} h_2$ 。左侧是K的元素，右侧是H的元素。因为 H∩K = { 1 },所以 $k_1 k_2^{-1} = h_1^{-1} h_2 = 1$ 。则 $k_1 = k_2$ , $h_1 = h_2$ ，且 $h_{1}k_{1}=h_{2}k_{2}$ 。

(b) 令 $(h_1, k_1)$ 和 $(h_2, k_2)$ 为乘法群 H×K 的元素。在乘法群 H×K 中的这些元素的乘积是 $(h_1 h_2 , k_1 k_2 )$ 以及 $f (h_1 h_2 , k_1 k_2 ) = h_1 h_2 k_1 k_2$ ，而 $f (h_1, k_1) f (h_2, k_2) = h_1 h_2 k_1 k_2$ 。当且仅当 $h_2 k_1 = h_1 k_2$ 时，这些元素是相等的。

(c) 假设 H 是一个不变子群。我们注意到 KH是一个左陪集kH与K中k的联合，而HK 是一个右陪集Hk的联合。因为H 是不变子群,所以 kH = Hk ，因此，HK = KH 。在乘法规则下HK的闭合可推导，因为 HKHK = HHKK = HK 。此外， $(hk)^{-1} = k^{-1} h^{-1}$ 在 KH = HK 中。这就证明了在可逆条件下 HK 的闭合性。

(d ) 假设H和K满足已知条件。且 f 既是单射又是满射，因此，它是双射。根据 (b),当且仅当对于H中的所有h，有 hk = kh 时，这个满射f 是一个同构。考虑交换子 $(hkh^{-1})k^{-1} = h(kh^{-1} k^{-1})$ 。因为K是不变子群，则左侧在K中，且又因为H是不变子群，因此，右侧也在H中。相反，如果f是一个同构，我们可以验证同构群 H × K 中列出的条件，而不是 G 中列出的条件。

我们使用这个命题来划分4阶群：

命题 1.11.5 4 阶群有两个同构类，即 4 阶循环群 C4 的类和Clein四群(Clein Four Group)的类，它于两个 2 阶群的乘积 $C_{2} \times C_{2}$ 是同构的。

证明：

令G为4阶群。G的任意元素x的阶数整除4，因此需要考虑两种情况：

情况一：G 包含 4 阶元素。则 G 是 4 阶循环群。

情况二：除恒等式外，G 中的每个元素的阶数均为 2。

在这种情况下，对于 G 的每个元素 x，有 $x=x^{-1}$ 。令 x 和 y 为 G 的两个元素。那么 xy 的阶数为 2，因此 $xyx^{-1} y^{-1}= (xy)( xy) = 1$ 。这表明 x 和 x 是可交换的 (2.6.5)，并且由于它们是任意元素，因此 G 是交换矩阵。所以每个子群都是不变子群。我们在 G 中选择不同的元素 x 和 y，并令 H 和 K 为它们生成的 2 阶循环群。命题 2.11.4 (d ) 表明 G 同构于乘积群 H×K 。

2.12 商群(QUOTIENT GROUPS)

在本节中，我们将证明可以在任何意群 G 的不变子群 N 的陪集构成的集合上定义合成律。该定律使不变子群的陪集集合成为一个群，称为商群(quotient groups)。

整数模n同余类的加法是商构造的一个示例。另一个熟悉的例子是角度的加法。每个实数表示一个角度，两个实数如果相差2π的整数倍则表示相同的角度。2π 整数倍群 N 是实数加法群 $\mathbb{R}^{+}$

的子群，而角度很自然地对应于 G 中 N 的(加法)陪集θ + N。角度群是商群，其元素是陪集。

一个群G 的不变子群 N 的陪集集合通常用 G/N 表示。

(2.12.1) G/N 是 G 中 N 的陪集集合。

当我们将陪集C 视为陪集构成的集合的一个元素时，可以使用方括号记法[C ]。若 C = aN ，我们也可以使用上划线记法 $\overline{a}$ 来表示元素 [C ],然后我们可以使用 $\overline{G}$ 来表示陪集集合：

$\overline{G} = G/N$ 。

定理 2.12.2 令 N 为一个群G的一个不变子群，并令 $\overline{G}$ 表示G 中 N 的陪集集合。关于 $\overline{G}$ 存在一个使得这个陪集的集合成为一个群的合成律，这个合成律使得由 $\pi (a)=\overline{a}$ 所定义的映射 $\pi:G \rightarrow \overline{G}$ 是一个以 N 为核的满射同态。

$\bullet$ 映射π通常称为从G 到 $\overline{G}$ 的标准映射(canonical map)。“canonical”这个词表明，这是可以合理地讨论的唯一映射。

下一个推论非常简单，但很重要，值得指出：

引理 2.12.3 令 N 为一个群G的一个不变子群，并令 $\overline{G}$ 表示G 中 N 的陪集集合。令 $\pi:G \rightarrow \overline{G}$ 为标准同态。令 $a_1 ,..., a_k$ 为使得乘积 $a_1 ... a_k$ 在N中的 G 的元素。则 $\overline{a_1 }... \overline{a_k }= \overline{1 }$ 。

证明：

令 $p = a_1 ... a_k$ 。则 p 在N中，因此, $\pi(p) =\overline{p}= \overline{1}$ 。因为π是同态， $\overline{a_1}... \overline{a_k}= \overline{p}$ 。

定理2.12.2的证明：

需要做几件事件。我们必须

$\bullet$ 在 $\overline{G}$ 上定义一个合成律，

$\bullet$ 并证明这个合成律使得 $\overline{G}$ 成为一个群，

$\bullet$ 证明π是满射同态，并且

$\bullet$ 证明π的核是N 。

我们使用下面的记法：若 A和 B是一个群 G 的子集，则 AB表示乘积 ab 的集合：

(2.12.4) AB = { x∈G | 对于某些 a∈A和 b∈B ，有 x = ab }。

我们将称此为一个积集(a product set)，但在某些其它的背景中，短语“product set”指的是元素对 A × B 的集合。

引理 2.12.5 令 N 为一个群G的一个不变子群，并令 aN 和 bN 为N的陪集。则积集 ( aN )( bN )也是一个陪集，它等于陪集abN。

我们注意，集合 ( aN )( bN ) 由G的可以写成形如 anbn’ 且 n和n’ 在 N 中的所有元素构成。

证明：

因为N是一个子群，NN = N 。再因为 N 是一个不变子群，其左右陪集是相等的：Nb = bN (2.8.17 )。根据下面的规范运算可以证明这个引理：

( aN )( bN ) = a(Nb ) N = a(bN )N = abNN = abN 。

这个引理允许我们基于集合 $\overline{G} = G/N$ 定义乘法。使用方括号记法(2.7.8)，定义为：若 $C_1$ 和 $C_2$ 是陪集，则 $[C_1][ C_2] = [C_1 C_2]$ ，其中， $C_1 C_2$ 是积集。这个引理证明了这个积集是另一个陪集。为了计算乘积 $[C_1][ C_2]$ ,取 $C_1$ 中的任意元素 a 和 $C_2$ 中的任意元素b 。若 $C_1 = aN$ 和 $C_2 = bN$ ，则 $C_1 C_2$ 是包含ab的陪集 abN 。因此，我们有非常自然的公式

(2.12.6) [aN][bN] = [abN ] 或 $\overline{a}\overline{b} = \overline{ab}$ 。

则根据(2.12.2)中映射π的定义，

(2.12.7) $\pi(a)\pi(b) = \overline{a}\overline{b} =\overline{ab}= \pi(ab)$ 。

一旦我们证明了 $\overline{G}$ 是一个群，则π是同态的这个事实将可以从(2.12.7)推导出。因为标准映射π是满射(2.7.8)，下一个引理证明这一点。

引理 2.12.8 令 G 为一个群，并令Y为一个具有一个合成律的集合，且与此相关的两个定律都使用乘法记法书写。令φ ：G ⟶ Y 为一个具有同态属性(即，对于G中的所有a和b，有 φ(ab) = φ(a)φ(b))的满射。则 Y是一个群，且 φ 是一个同态。

证明：

在G中成立的公理通过满射φ 被搬运到Y。此为结合律的证明：令 $y_1 ,y_2 ,y_3$ 为Y的元素。困为φ是满射的，所以，对于G中的某些 $x_i$ ，有 $y_i = \varphi(x_i)$ 。则

$(y_1 y_2)y_3 = (\varphi(x_1) \varphi(x_2))\varphi(x_3) = \varphi(x_1 x_2)\varphi(x_3) = \varphi((x_1 x_2)x_3)$

-------------⩮ $\varphi(x_1(x_2 x_3)) = \varphi(x_1)\varphi(x_2 x_3) = \varphi(x_1)( \varphi(x_2)\varphi(x_3)) = y_1(y_2 y_3)$ 。

带星的等号( ⩮ ,Unicode编码“U+02A6E”,LaTex语法“\asteq”)是G中的结合律。其它的等式可以从φ的同态推导出。其它群定理有验证类似。

剩下唯一需要验证的事情是同态π的核是子群N 。这个不难，当且仅当 $\overline{a}=1$ 或 [aN] = [1N] 时，有 π(a) = π(1)，且当且仅当 a 是N的一个元素时，这也成立。

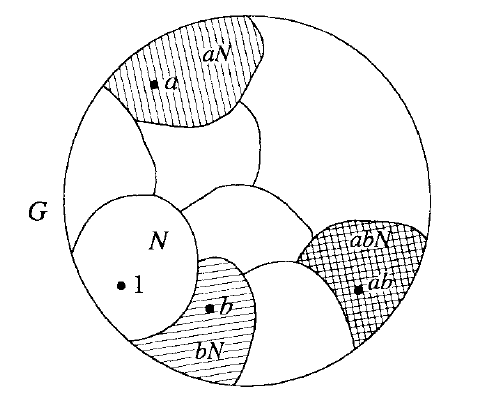
(2.12.9) -------------------------陪集乘法的示意图----------------------。

注意：对于引理 2.12.5,我们的假设——N为G的一个不变子群，这一点至关重要。假如 N不是一个不变子群，将会留下 G 中 H 的陪集 $C_1$ 和 $C_2$ ，使得积集 $C_1C_2$ 不在一个单左陪集中。再次回到 $S_3$ 的子群 H = < y > ，积集由 (1H )(xH )包含4个元素： $\{1,y \}\{x ,xy \} = \{ x,xy,x^2y, x^2 \}$

。它不是一个陪集。子群 H 不是一个不变子群。

下面的定理将商群构造与一个不变子群同态并联起来，并提供了一种识别商群的基本方法。

定理 2.12.10 第一同构定理：令 φ ：G ⟶ G ’ 为一个核为 N的满射群同态。商群 $\overline{G} = G/N$ 与像 G ’ 是同构的。为准确起见，令π：G ⟶ G ’ 为标准映射。则存在一个唯一的同构 $\overline{\varphi}:\overline{G} \rightarrow G'$ ，使得 $\varphi=\overline{\varphi} \circ \pi$ (译注：“⚬”的LaTex语法名称“medium small white circle”。)

证明：

$\overline{G}$ 的元素是N的陪集，并且它们也是映射φ (2.7.15) 的纤维。在定理中涉及到的映射 $\overline{\varphi}$ 是一个将一个非空纤维发送到其像 $\overline{\varphi}(\overline{x})=\varphi(x)$ 的映射。对于集合的任意满射φ ：G ⟶ G ’ ，我们可以构成纤维的集合 $\overline{G}$ ，然后，我们可以获得以上的三角形状的关系图，其中 $\overline{\varphi}$ 是一个将一个纤维发送到其像的双射。当 φ是一个群同态的时候， $\overline{\varphi}$ 是一个同构，原因在于 $\overline{\varphi}( \overline{ab}) = \varphi(ab) = \varphi(a)\varphi(b) = \overline{\varphi}(\overline{a}) \overline{\varphi}(\overline{b})$ 。

引理 2.12.11 令 φ ：G ⟶ G’ 为一个核为 N且像为H’ 的群同态。则商群 $\overline{G} = G/N$ 与像 H’ 是同构的。

(根据定义)立即就能给出两个例子：绝对值映射 $\mathbb{C}^{\times} \longrightarrow \mathbb{R}^{\times}$ 的像是正实数群，其核是单位圆 U 。这个定理断言，商群 $\mathbb{C}^{\times}/U$ 正实数乘法群是同构的。行列式是一个满射同态 $GL_n(\mathbb{R}) \rightarrow \mathbb{R}^{\times}$ ，其核是特别线性群 $SL_n(\mathbb{R})$ 。因此，商群 $GL_n(\mathbb{R})/SL_n(\mathbb{R})$ 与 $\mathbb{R}^{\times}$ 是同构的。

此外，还有被称为第二同态定理，第三同态定理的定理，只不过它们不太重要。

内容来源：

<<Algebra>> Michael Artin, 2th

参考资料：

<<An introduction to the theory of groups>> Rotman
<<THE CLASSICAL GROUPS>> HERMANN WEYL
<<discovering-group-theory>> Tony Barnard,Hugh Neill
<<An introduction to group theory>> Tony Gaglione