buildroot移植Qt5无法显示字体问题

news2024/12/29 1:28:53

报错：QFontDatabase: Cannot find font directory /usr/lib/fonts.
Note that Qt no longer ships fonts. Deploy some (from DejaVu Fonts for example) or switch to fontconfig.

    原因：很明显是Qt没有找到字库文件；

    解决方法： 1、将Windows电脑上\Windows\Fonts下拷贝字体（ttf后缀）拷贝到目标平台/usr/lib/fonts/目录下可以解决；

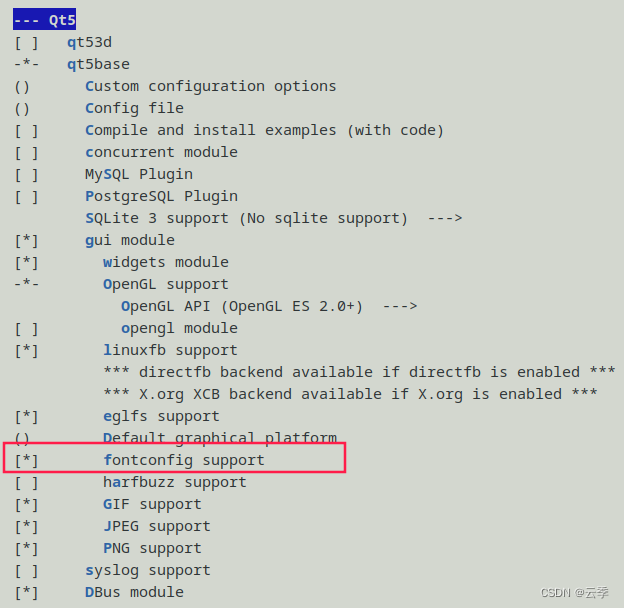
                       2、根本原因是由于设备使用了fontconfig，但是一开始Qt5没有配置QT5BASE_FONTCONFIG导致Qt无法找到字库， 将QT5BASE_FONTCONFIG配置为Y后重新编译Qt即可解决，记得要重编Qt。
BR2_PACKAGE_QT5BASE_FONTCONFIG=y

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1040843.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

排查内存泄露

排查内存泄露

1 通过Performance确认是否存在内存泄露 一个存在内存泄露的 DEMO 代码&#xff1a; App.vue <template><div><button click"myFn" style"width: 200px; height: 200px;"></button><home v-if"ishow"></hom…
阅读更多...
VUE使用DXFParser组件解析dxf文件生成图片

VUE使用DXFParser组件解析dxf文件生成图片

<template><div><input type"file" change"handleFileChange" /></div><el-table :data"tableData" style"width: 100%"><el-table-column prop"Control_No" label"序号" width…
阅读更多...
图像处理与计算机视觉--第四章-图像滤波与增强-第一部分

图像处理与计算机视觉--第四章-图像滤波与增强-第一部分

目录 1.灰度图亮度调整 2.图像模板匹配 3.图像裁剪处理 4.图像旋转处理 5.图像邻域与数据块处理 学习计算机视觉方向的几条经验: 1.学习计算机视觉一定不能操之过急&#xff0c;不然往往事倍功半&#xff01; 2.静下心来&#xff0c;理解每一个函数/算法的过程和精髓&…
阅读更多...
C语言入门Day_25 函数与指针小结

C语言入门Day_25 函数与指针小结

目录 前言&#xff1a; 1.函数 2.指针 3.易错点 4.思维导图 前言&#xff1a; 函数就像一个“有魔法的加工盒”&#xff0c;你从入口丢一些原材料进去&#xff0c;它就能加工出一个成品。不同的函数能加工出不同的成品。 入口丢进去的瓶子&#xff0c;水和标签就是输入&a…
阅读更多...
win使用git（保姆级教程）

win使用git（保姆级教程）

序言 上学期间用的git并不多&#xff0c;但是从研三实习以及后面工作来看&#xff0c;git是一项必备技能&#xff0c;所以在此来学习一下。 下载git安装包 打开网站&#xff0c;根据需求来下载&#xff1b;一般按照如下方式进行下载&#xff1a; 然后安装的时候记得按下图勾…
阅读更多...
NebulaGraph实战：3-信息抽取构建知识图谱

NebulaGraph实战：3-信息抽取构建知识图谱

自动信息抽取发展了几十年&#xff0c;虽然模型很多&#xff0c;但是泛化能力很难用满意来形容&#xff0c;直到LLM的诞生。虽然最终信息抽取质量部分还是需要专家审核&#xff0c;但是已经极大的提高了信息抽取的效率。因为传统方法需要大量时间来完成数据清洗、标注和训练&am…
阅读更多...
32.栈的应用补充-表达式求值

32.栈的应用补充-表达式求值

目录 一. 前缀表达式与后缀表达式 二. 中缀表达式转后缀表达式的手算方法 三. 后缀表达式的手算方法 四. 后缀表达式的机算方法 五. 中缀表达式转前缀表达式的手算方法 六. 前缀表达式的机算方法 七. 中缀表达式转后缀表达式的机算方法 八. 中缀表达式的机算 一. 前缀表…
阅读更多...
ElementUI首页导航和左侧菜单静态页面的实现，以及Mockjs和总线的介绍

ElementUI首页导航和左侧菜单静态页面的实现，以及Mockjs和总线的介绍

目录 前言 一. Mock.js 1.1 什么是Mock.js 1.2 Mockjs的安装与配置 1.2.1 安装Mock.js 1.2.2 引入Mock.js 1.3 Mockjs的使用 1.3.1 定义数据测试文件 1.3.2 mock拦截ajax请求 二. 首页导航以及左侧菜单的搭建 2.1 什么是总线 2.2 创建三个vue组件 首页AppMain.vue组…
阅读更多...
Learn Prompt- Midjourney Prompt:Prompt 提示语

Learn Prompt- Midjourney Prompt:Prompt 提示语

基础结构​ 一个基本的提示可以简单到一个单词、短语或表情符号。非常短的提示将在很大程度上依赖于 Midjourney 的默认样式。 完整 prompt&#xff1a;可以包括一个或多个图像链接、多个文本短语或单词&#xff0c;以及一个或多个后缀参数 Image Prompts: 可以将图像 URL 添加…
阅读更多...
Vue中前端导出word文件

Vue中前端导出word文件

很多时候在工作中会碰到完全由前端导出word文件的需求&#xff0c;因此特地记录一下比较常用的几种方式。 一、提供一个word模板 该方法提供一个word模板文件&#xff0c;数据通过参数替换的方式传入word文件中&#xff0c;灵活性较差&#xff0c;适用于简单的文件导出。需要…
阅读更多...
Postgresql源码（113）表达式JIT计算简单分析

Postgresql源码（113）表达式JIT计算简单分析

相关 《Postgresql源码&#xff08;85&#xff09;查询执行——表达式解析器分析&#xff08;select 11如何执行&#xff09;》 《Postgresql源码&#xff08;113&#xff09;表达式JIT计算简单分析》 1 普通表达式计算 普通表达式计算发生在优化器preprocess_expression中&am…
阅读更多...
uni-app 使用 scss 实现推荐标签区域显示效果

uni-app 使用 scss 实现推荐标签区域显示效果

效果图 <view class"tag-box"><view class"tag-tip"><view>店家</view><view>推荐</view></view> </view> 方法一 只需修改 $tagFontSize(字体大小) 即可 /* 推荐标签区域 */ .tag-box {$tagFontSize:…
阅读更多...
uni-app：实现元素中实现竖直居中

uni-app：实现元素中实现竖直居中

效果展示 前&#xff1a; 后&#xff1a; 未实现前代码 <template><view class"container"><view class"centered-element">我是要被居中的元素</view></view> </template><script>export default {data() {r…
阅读更多...
算法与数据结构-堆

算法与数据结构-堆

文章目录 什么是堆如何实现一个堆&#xff1f;如何基于堆实现排序&#xff1f;1. 建堆2. 排序 什么是堆 堆是一种特殊的树&#xff0c;特殊点有二&#xff0c;如下&#xff1a; 堆是一个完全二叉树&#xff1b;堆中每一个节点的值都必须大于等于&#xff08;或小于等于&#…
阅读更多...
【Vue】Mock.js介绍和使用与首页导航栏左侧菜单搭建

【Vue】Mock.js介绍和使用与首页导航栏左侧菜单搭建

目录 一、Mock.js 1.1 mockjs介绍 1.2 mock.js安装与配置 1.2.1 安装mock.js 1.2.2 引入mock.js 1.3 mock.js的使用 1.3.1 准备模拟数据 1.3.2 定义拦截路由 1.3.3 测试 二、首页导航栏左侧菜单搭建 2.1 自定义界面组件 (完整代码) 2.2 配置路由 2.3 组件显示折叠和…
阅读更多...
uniapp ui安装

uniapp ui安装

安装 ui uni-app官网 (dcloud.net.cn) 安装 pages.js配置 使用 <template><view class"bg"><div class"title"><uni-data-selectv-model"value":localdata"range"change"change">asa</uni-da…
阅读更多...
GiliSoft USB Lock v10.5.0 电脑USB设备管控软件

GiliSoft USB Lock v10.5.0 电脑USB设备管控软件

网盘下载 软件功能特性 禁止USB / SD驱动器 禁用从USB / SD磁盘读取&#xff0c;禁用写入USB / SD磁盘&#xff0c;阻止非系统分区。它不允许任何类型的USB / SD驱动器访问您的计算机&#xff0c;除非您授权它或它已在可信设备白名单。 CD锁&#xff0c;块媒体和蓝光光盘 禁用…
阅读更多...
代码阅读分析神器-Scitools Understand

代码阅读分析神器-Scitools Understand

这里写目录标题 前言概要功能介绍1.代码统计2.图形化分析3.代码检查 使用方法下载及使用 前言 作为一名程序员&#xff0c;阅读代码是一个必须要拥有的能力&#xff0c;但无奈很多代码逻辑嵌套非常多&#xff0c;看起来非常吃力&#xff0c;看了那段逻辑就忘记了刚才的逻辑&am…
阅读更多...
Spring实例化源码解析之ComponentScanAnnotationParser(四)

Spring实例化源码解析之ComponentScanAnnotationParser(四)

上一章我们分析了ConfigurationClassParser&#xff0c;配置类的解析源码分析。在ComponentScans和ComponentScan注解修饰的候选配置类的解析过程中&#xff0c;我们需要深入的了解一下ComponentScanAnnotationParser的parse执行流程&#xff0c;SpringBoot启动类为什么这么写&…
阅读更多...
01 MIT线性代数-方程组的几何解释

01 MIT线性代数-方程组的几何解释

一, 线性方程的几何图像 The geometry of linear equations 线性代数的基本问题就是解n元一次方程组 eg&#xff1a;二元一次方程组 矩阵形式: 系数矩阵(coefficient matrix): 未知数向量: 线性方程组简记为Axb 二, 行图像 Row Picture 行图像遵从解析几何的描述&#xff0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023