目录
一. 前缀表达式与后缀表达式
二. 中缀表达式转后缀表达式的手算方法
三. 后缀表达式的手算方法
四. 后缀表达式的机算方法
五. 中缀表达式转前缀表达式的手算方法
六. 前缀表达式的机算方法
七. 中缀表达式转后缀表达式的机算方法
八. 中缀表达式的机算

一. 前缀表达式与后缀表达式
让我们从大家熟悉的表达式说起:((15÷(7 -(1 +1))) × 3)-(2 +(1 +1))。表达式由三个部分组成:操作数、运算符、界限符。其中界限符不可省略,它反映了运算的先后顺序。
某波兰数学家就想:我们能否不用界限符也可以无歧义的表达运算顺序?答案显然是可以的,这就是“波兰表达式”(前缀表达式)和“逆波兰表达式”(后缀表达式)。
前缀表达式:二目运算符+操作数1+操作数2;后缀表达式:操作数1+操作数2+二目运算符
例如:
| 中缀表达式 | 前缀表达式 | 后缀表达式 |
| a+b | +ab | ab+ |
| a+b-c | -+abc | ab+c- |
| a+b-c*d | -+ab*cd | ab+cd*- |
需要说明的是,由于确定中缀表达式的各个运算符的运算顺序不同(例如第3个既可以先算a+b也可以先算c*d),同一中缀表达式转化的前缀表达式和后缀表达式也可能不同。
二. 中缀表达式转后缀表达式的手算方法
- 确定中缀表达式中各个运算符的运算顺序;
- 选择下一个运算符,按照[左操作数 右操作数 运算符]的方式组合成一个新的操作数;
- 如果还有运算符没被处理,就继续2;
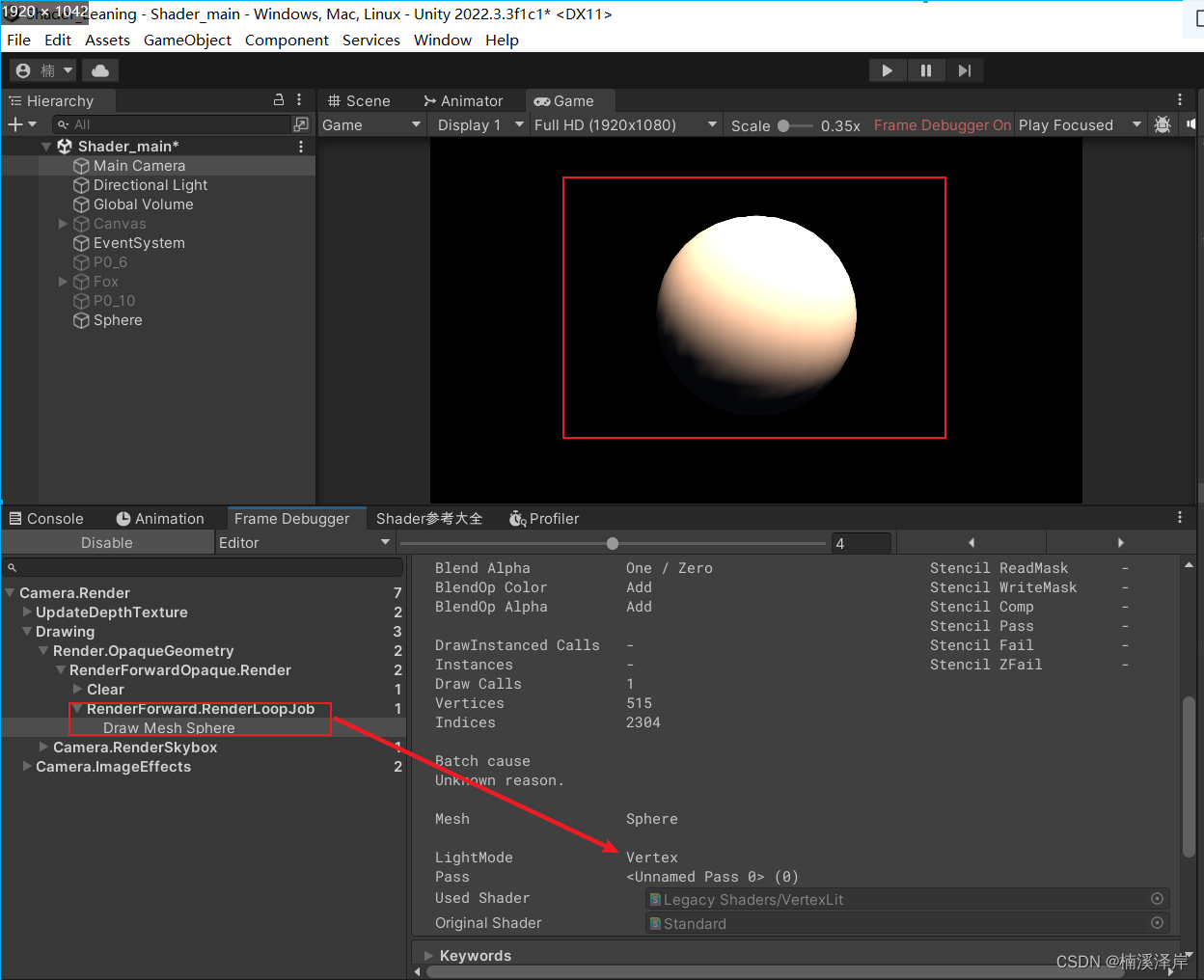
例如:前面的中缀表达式各运算符顺序确定如下:

在后缀表达式中,1 1 +先作为一个操作数,然后用7减去,就是7 1 1 + -,再用15除,就是15 7 1 1 + - /,以此类推。
再如,对同一中缀表达式确定不同的运算符顺序:

客观来看两种都正确。但是如果用计算机实现转换,算法需要有确定性,显然前面一种转化运算符的顺序就是运算顺序。更优。
那么如何保证对中缀表达式计算得到后缀表达式的时候,运算符的顺序就是运算顺序呢?显然我们要在确定中缀表达式的运算符运算顺序时不要FreeStyle。这里应当采用所谓“左优先”原则,即:要左边的运算符能先计算,就优先算左边的。
例如:对下面的中缀表达式,确定运算符顺序如下:

三. 后缀表达式的手算方法
方法:从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应运算,合体为一个操作数。应当注意:两个操作数的左右顺序问题。


后缀表达式的特点是:最后出现的操作数被最先计算。
四. 后缀表达式的机算方法
前面说到后缀表达式的特点是:最后出现的操作数被最先计算。这就很完美符合栈的后进先出的特点。接下来讲如何利用栈实现机算。这里栈是操作数栈
- 从左往右扫描下一个元素,直到处理完所有元素;
- 若扫描到操作数则压入栈,并回到1,否则执行3;
- 若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶,回到1;
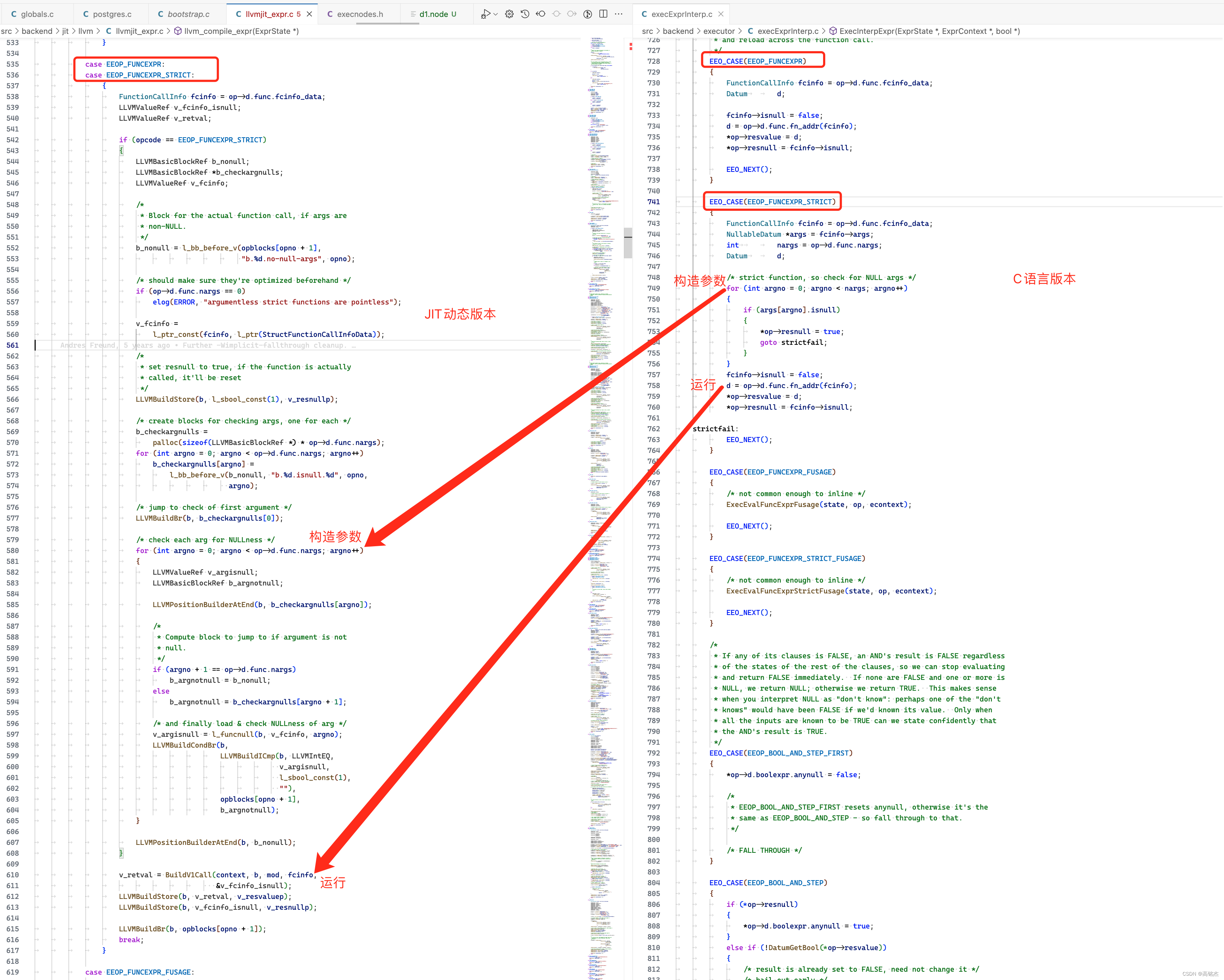
以(三)中的第2张图为例:A入栈-B入栈-扫描到+,弹出A和B,执行完A+B后把(A+B)压入栈内-C入栈-D入栈-扫描到*,弹出C和D,执行C*D中把(C*D)压入栈内-E入栈-扫描到/,弹出E和(C*D)【注意先出栈的是右操作数】,执行(C*D)/E后把结果压入栈内-扫描到—,把(C*D)/E和(A+B)弹出,计算(A+B)-(C*D)/E后压入栈内-F入栈-扫描到+,弹出F和(A+B)-(C*D)/E,执行完(A+B)-(C*D)/E+F后压入栈内-扫描结束,这个时候栈内只剩一个元素,它就是最终结果(A+B)-(C*D)/E+F。
五. 中缀表达式转前缀表达式的手算方法
- 确定中缀表达式中各个运算符的运算顺序;
- 选择下一个运算符,按照「运算符 左操作数 右操作数」的方式组合成一个新的操作数;
- 如果还有运算符没被处理,就继续2;
相似的,为了得到唯一表达式,采用“右优先”原则:只要右边的运算符能先计算,就优先算右边的。例如下面的表达式,选择右面的计算顺序可以得到倒序的运算顺序。

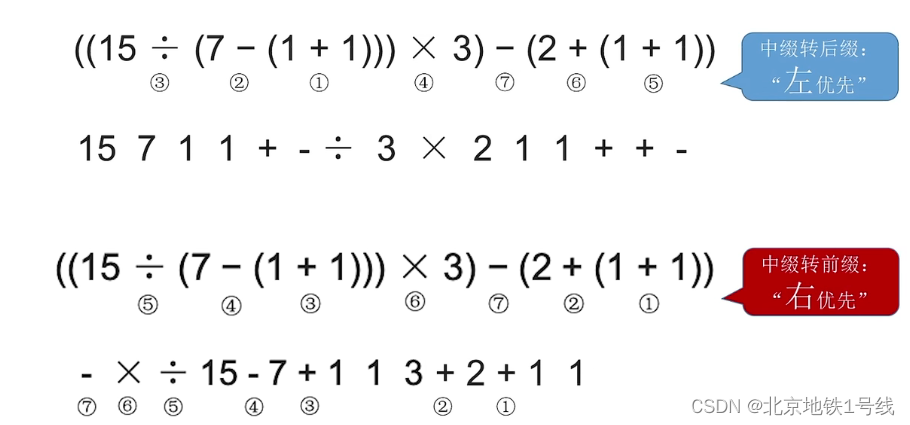
六. 前缀表达式的机算方法
此部分和(四)类似,只不过是从右往左扫描:
- 从右往左扫描下一个元素,直到处理完所有元素;
- 若扫描到操作数则压入栈,并回到1;否则执行3;
- 若扫描到运算符,则弹出两个栈顶元素,执行相应运算【注意:先出栈的是左操作数】,运算结果压回栈顶,回到1;
七. 中缀表达式转后缀表达式的机算方法
初始化一个栈,用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况:
- 遇到操作数。直接加入后缀表达式。
- 遇到界限符。遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止。注意:“(”和“)”不加入后缀表达式。
- 遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,若碰到“(”或栈空则停止。之后再把当前运算符入栈。
按上述方法处理完所有字符后,将栈中剩余运算符依次弹出,并加入后缀表达式。
仍然以(三)中的第2张图为例:初始化一个用来存放运算符的栈。
从前到后扫描中缀表达式:A直接加入后缀表达式—+号入栈—B直接加入后缀表达式—扫描到-,+从栈弹出加入后缀表达式,然后-入栈—C直接加入后缀表达式—*入栈—D直接加入后缀表达式—扫描到/,*从栈弹出加入后缀表达式,然后/入栈—E直接加入后缀表达式—扫描到+,/和-依次从栈弹出并加入后缀表达式,然后+入栈—F直接加入后缀表达式—扫描结束,此时栈内只有一个+,把+输出加入到后缀表达式中。
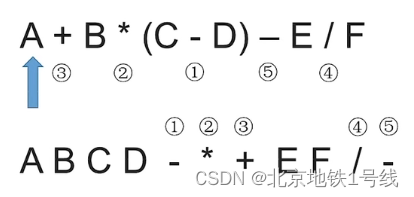
我们再看一个带括号的中缀表达式:A直接加入后缀表达式—+号入栈—B直接加入后缀表达式—*入栈—(直接入栈—C直接加入后缀表达式—扫描到-,此时运算符栈顶元素是(,所以直接把-入栈—D直接加入后缀表达式—扫描到),此时栈底到栈顶有+,*,(,-,依次从栈顶全部弹出【(不进入后缀表达式】—“-”号入栈—E直接加入后缀表达式—扫描到/,入栈—F直接加入后缀表达式—扫描结束,此时栈内有-,/,依次输出/和-,结束。
八. 中缀表达式的机算
其实就是(七)和(四)的结合。
- 初始化两个栈,操作数栈和运算符栈;
- 若扫描到操作数,压入操作数栈;
- 若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈);
仍然以(三)中的第2张图为例:A入操作数栈—+入运算符栈—B入操作数栈—扫描到-,弹出运算符等级相同的+,并从操作数栈弹出A和B,计算A+B后压回操作数栈,最后-号入运算符栈—C入操作数栈—*入运算符栈—D入操作数栈—扫描到/,弹出运算符*,同时弹出C和D,计算C*D后压回操作数栈,最后把/压入运算符栈—E入操作数栈—扫描到+,/和-依次弹出。弹出/时计算C*D/E,压回操作数栈中,然后弹出-时计算A+B-C*D/E,压回操作数栈中,最后把+压入运算符栈—F入操作数栈—扫描结束,把运算符栈清空,每弹出一个运算符弹出两个操作数,这样就是A+B-C*D/E+F。