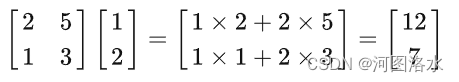一, 线性方程的几何图像 The geometry of linear equations
线性代数的基本问题就是解n元一次方程组
eg:二元一次方程组
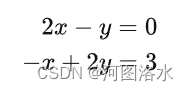
矩阵形式:
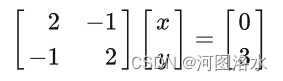
系数矩阵(coefficient matrix):
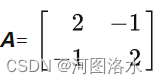
未知数向量:

线性方程组简记为Ax=b
二, 行图像 Row Picture
行图像遵从解析几何的描述,每个方程在平面上的图像为一条直线。找到符合方程的两个数组,就可以确定出x-y平面上的两个点,连接两点可以画出该方程所代表的直线。两直线交点即为方程组的解x=1,y=2
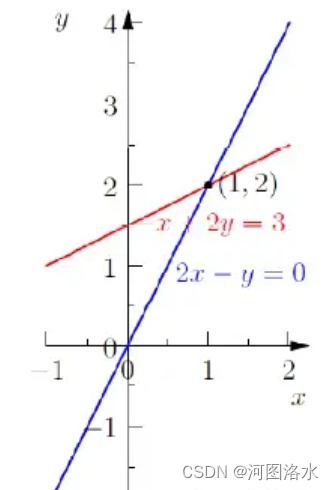
三, 列图像 Column Picture
在列图像中,我们将系数矩阵写成列向量的形式,则求解原方程变为寻找列向量的线性组合(linear combination)来构成向量b
linear combination of columns 向量线性组合是贯穿本课程的重要概念。对于给定的向量c和d以及标量x和y,我们将xc+yd称之为c和d的一个线性组合
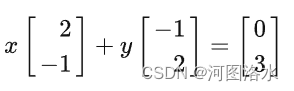
从几何上讲,我们是寻找满足如下要求的x和y,使得两者分别数乘对应的列向量之后相加得到向量
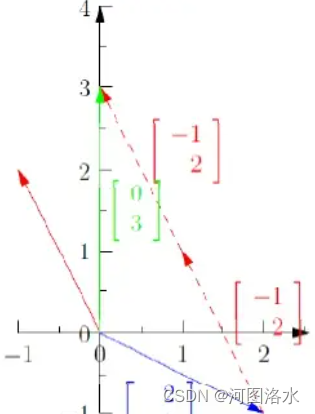
可以看到当蓝色的向量乘以1与红色的向量乘以2后做加法(首尾相接)就可以得到绿色的向量b= ,由此可得到方程的解x=1,y=2
,由此可得到方程的解x=1,y=2
想象一下如果任意取x,y,则得到的线性组合又是什么?其结果就是以上两个列向量的所有线性组合将会布满整个坐标平面。
四, 扩展到三元

4.1 row picture

three planes meet at one point
4.2 column picture

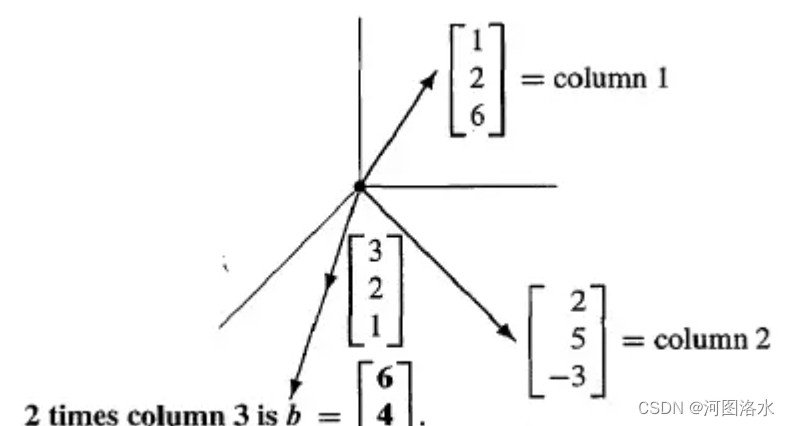
如果改变等号右侧的b的数值,那么对于行图像而言三个平面都改变了,而对于列图像而言,三个向量并没有发生变化,只是需要寻找一个新的组合
Can U solve Ax=b for every b? 是否对于所有的b,方程Ax=b都有解?
转化为
Do the linear combs of the columns fill 3-d space? 列向量的线性组合是否覆盖整个三维空间
For this A(non-singular非奇异, invertible可逆) answer is yes
反例:若三个向量在同一平面内——比如“列3”恰好等于“列1”加“列2”,而若b不在该平面内,则三个列向量无论怎么组合也得不到平面外的向量b。此时矩阵A为奇异阵或称不可逆矩阵。在矩阵A不可逆条件下,不是所有的b都能令方程Ax=b有解
对n维情形则是,n个列向量如果相互独立——“线性无关”,则方程组有解。否则这n个列向量起不到n个的作用,其线性组合无法充满n维空间,方程组未必有解
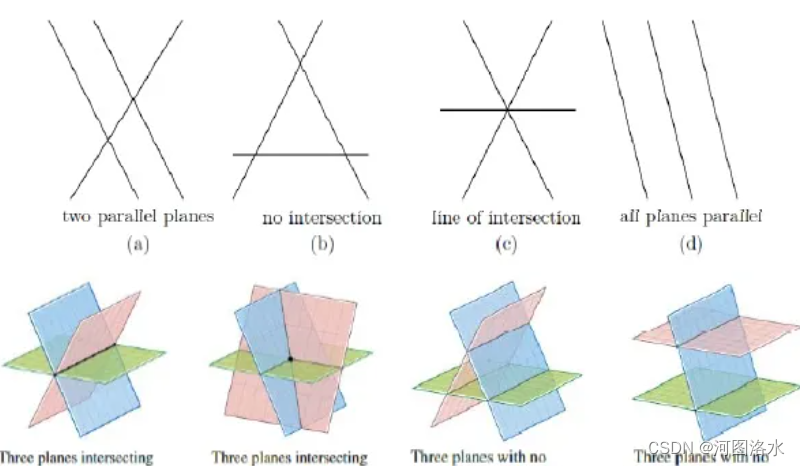
从行图像的角度来看,三元方程组是否有解意味着什么?当方程所代表的三个平面相交于一点时方程有唯一解;三个平面中至少两个平行则方程无解;平面的两两交线互相平行方程也无解;三个平面交于一条直线则方程有无穷多解。
五, 矩阵与向量的乘法
列图像:Ax是矩阵A列向量的线性组合 Ax is a comb of columns
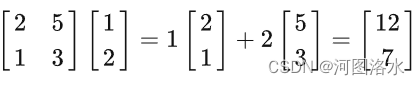
也可以通过将矩阵A的行向量和x向量进行点积来计算