给你两棵二叉树,原始树 original 和克隆树 cloned,以及一个位于原始树 original 中的目标节点 target。
其中,克隆树 cloned 是原始树 original 的一个 副本 。
请找出在树 cloned 中,与 target 相同 的节点,并返回对该节点的引用(在 C/C++ 等有指针的语言中返回 节点指针,其他语言返回节点本身)。
注意:你 不能 对两棵二叉树,以及 target 节点进行更改。只能 返回对克隆树 cloned 中已有的节点的引用。
示例 1:
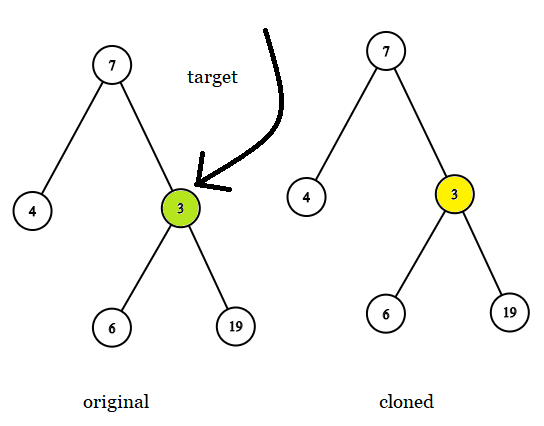
输入: tree = [7,4,3,null,null,6,19], target = 3 输出: 3 解释: 上图画出了树 original 和 cloned。target 节点在树 original 中,用绿色标记。答案是树 cloned 中的黄颜色的节点(其他示例类似)。
示例 2:
输入: tree = [7], target = 7 输出: 7
示例 3:
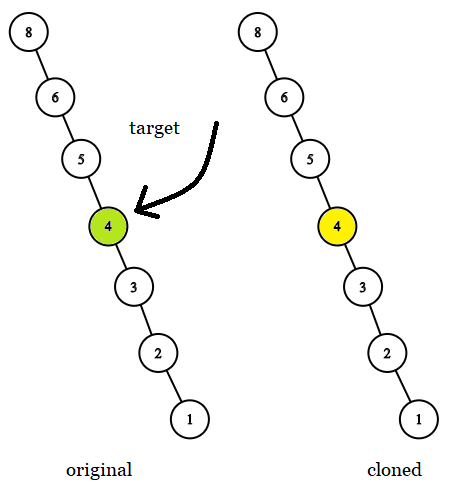
输入: tree = [8,null,6,null,5,null,4,null,3,null,2,null,1], target = 4 输出: 4
提示:
- 树中节点的数量范围为
[1, 104]。 - 同一棵树中,没有值相同的节点。
target节点是树original中的一个节点,并且不会是null。
一、信息
1.给我两个二叉树,一个是原始树,一个是克隆树,以及目标节点target。
2.克隆树是原始树的一个副本(这句话什么意思?)
3.克隆树是原始树的一个副本。
4.请找出树中target相同的节点,并返回对该节点的引用。
七、我的答案:
为了解决这个问题,我们需要采用DFS(深度优先搜索)或BFS(广度优先搜索)在克隆树`cloned`中查找与`original`中的`target`节点值相同的节点。因为题目说明树中没有值相同的节点,我们可以通过比较节点的值来找到目标节点。我们不会更改任何树的结构,只会返回目标节点的引用。
以下是C语言、C++和Java中实现的代码:
### C语言
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
};
struct TreeNode* getTargetCopy(struct TreeNode* original, struct TreeNode* cloned, struct TreeNode* target) {
if (!cloned) return NULL;
if (cloned->val == target->val) return cloned;
struct TreeNode* left = getTargetCopy(original, cloned->left, target);
if (left) return left;
return getTargetCopy(original, cloned->right, target);
}### C++
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
TreeNode* getTargetCopy(TreeNode* original, TreeNode* cloned, TreeNode* target) {
if (!cloned) return nullptr;
if (cloned->val == target->val) return cloned;
TreeNode* left = getTargetCopy(original, cloned->left, target);
if (left) return left;
return getTargetCopy(original, cloned->right, target);
}
};### Java
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
class Solution {
public final TreeNode getTargetCopy(final TreeNode original, final TreeNode cloned, final TreeNode target) {
if (cloned == null) return null;
if (cloned.val == target.val) return cloned;
TreeNode left = getTargetCopy(original, cloned.left, target);
if (left != null) return left;
return getTargetCopy(original, cloned.right, target);
}
}
思考过程和分析过程
我们使用递归DFS来遍历二叉树的每一个节点。对于当前的节点,我们首先检查它是否是我们正在寻找的`target`,如果是,则返回当前的`cloned`节点。如果不是,我们会递归地在左子树和右子树中查找。如果在左子树中找到了目标节点,我们会立即返回,不再在右子树中查找。
此算法的时间复杂度是O(n),其中n是二叉树中节点的数量,因为在最坏的情况下我们可能需要遍历所有节点。空间复杂度是O(h),其中h是树的高度,即递归栈的最大深度。
进阶:如果树中允许出现值相同的节点,将如何解答?
如果树中允许出现值相同的节点,我们无法仅通过节点的值来找到目标节点。这种情况下,我们需要同时遍历原始树`original`和克隆树`cloned`,并比较`original`中的节点是否与`target`相同,如果相同,则返回`cloned`树中对应的节点。
### C语言
struct TreeNode* getTargetCopy(struct TreeNode* original, struct TreeNode* cloned, struct TreeNode* target) {
if (!original) return NULL;
if (original == target) return cloned;
struct TreeNode* left = getTargetCopy(original->left, cloned->left, target);
if (left) return left;
return getTargetCopy(original->right, cloned->right, target);
}### C++
class Solution {
public:
TreeNode* getTargetCopy(TreeNode* original, TreeNode* cloned, TreeNode* target) {
if (!original) return nullptr;
if (original == target) return cloned;
TreeNode* left = getTargetCopy(original->left, cloned->left, target);
if (left) return left;
return getTargetCopy(original->right, cloned->right, target);
}
};### Java
class Solution {
public final TreeNode getTargetCopy(final TreeNode original, final TreeNode cloned, final TreeNode target) {
if (original == null) return null;
if (original == target) return cloned;
TreeNode left = getTargetCopy(original.left, cloned.left, target);
if (left != null) return left;
return getTargetCopy(original.right, cloned.right, target);
}
}### 分析过程
1. **比较原始节点与目标节点**:
在遍历时,我们比较原始树`original`的当前节点是否与`target`相同。如果相同,我们返回克隆树`cloned`中相对应的节点。
2. **递归遍历**:
如果原始树的当前节点不是目标节点,我们递归地在左子树和右子树中查找。我们同步遍历原始树`original`和克隆树`cloned`。
3. **返回结果**:
如果在左子树中找到了目标节点,我们会立即返回,不再在右子树中查找。如果左子树中没有找到,我们会继续在右子树中查找。
这个解决方案的时间复杂度和空间复杂度与前一个相同,即O(n)的时间复杂度和O(h)的空间复杂度,其中n是树中的节点数量,h是树的高度。
总结:
通过这道题目,我们可以学到几个重要的知识点和技能:
### 1. **二叉树的遍历**
这道题目展示了如何使用深度优先搜索(DFS)来遍历二叉树的每一个节点。通过递归地遍历左子树和右子树,我们可以访问二叉树中的每一个节点。这是解决许多二叉树问题的基础技能。
### 2. **递归**
这个问题展示了递归是如何应用于二叉树的遍历中的。通过递归的左、右子树调用,我们可以简洁、清晰地编写代码来遍历整棵树。
### 3. **指针和引用**
在C和C++实现中,我们使用指针来访问和返回树的节点。在Java中,我们通过引用来实现。理解如何在不同的编程语言中使用指针和引用是理解这道题目的关键。
### 4. **同步遍历**
在进阶部分,我们学习了如何同步遍历两棵二叉树。这是一种重要的技巧,尤其是当你需要比较两棵树的结构或值时。
### 5. **理解问题约束**
开始时,题目中提到树中没有值相同的节点,所以我们可以简单地通过比较节点的值来找到目标节点。但在进阶问题中,我们需要更仔细地思考如何在允许值相同的情况下找到正确的节点。我们学会了如何根据问题的不同约束来调整我们的解决方案。
### 6. **代码的适应性和可扩展性**
这道题展示了如何编写可以应对不同需求变化的代码。当问题约束发生变化时(例如,当树中允许有相同值的节点时),我们应该能够灵活地调整我们的代码以适应新的需求。
### 7. **问题分析**
最后,这个问题也教会了我们如何分析问题,理解问题的需求和约束,并根据这些需求和约束来制定解决方案。这包括理解时间复杂度和空间复杂度,以及如何优化它们来满足可能的性能要求。