目录
第一题
题目来源
题目内容
解决方法
方法一:滑动窗口
方法二:哈希表和双指针
方法三:动态规划
第二题
题目来源
题目内容
解决方法
方法一:深度优先搜索(DFS)
方法二:树结构
第三题
题目来源
题目内容
解决方法
方法一:遍历交换
方法二:递归
方法三:字典序法
第一题
题目来源
30. 串联所有单词的子串 - 力扣(LeetCode)
题目内容


解决方法
方法一:滑动窗口
- 首先,统计words数组中每个单词的出现次数,并存储在wordCount中。
- 然后,通过遍历字符串s的所有可能起始位置,以总长度为totalLength进行滑动窗口操作。在每个窗口中,使用临时的tempCount和count变量来记录窗口内的单词出现次数。如果窗口内的单词出现次数符合要求,在结果列表中添加当前起始位置。
- 最后,返回结果列表。
import java.util.*;
class Solution {
public List<Integer> findSubstring(String s, String[] words) {
List<Integer> result = new ArrayList<>();
if (s == null || s.length() == 0 || words == null || words.length == 0) {
return result;
}
int wordLength = words[0].length();
int totalLength = words.length * wordLength;
Map<String, Integer> wordCount = new HashMap<>();
for (String word : words) {
wordCount.put(word, wordCount.getOrDefault(word, 0) + 1);
}
for (int i = 0; i <= s.length() - totalLength; i++) {
Map<String, Integer> tempCount = new HashMap<>(wordCount);
int count = words.length;
for (int j = 0; j < totalLength; j += wordLength) {
String word = s.substring(i + j, i + j + wordLength);
if (tempCount.containsKey(word)) {
int freq = tempCount.get(word);
if (freq == 1) {
tempCount.remove(word);
} else {
tempCount.put(word, freq - 1);
}
count--;
} else {
break;
}
}
if (count == 0) {
result.add(i);
}
}
return result;
}
}
复杂度分析:
时间复杂度:
- 首先需要遍历字符串s的所有可能起始位置,此操作的时间复杂度为O(N),其中N是s的长度。
- 在每个起始位置,需要遍历words数组,对于每个单词,需要使用s.substring()方法获取指定位置的子串,并进行比较。此操作的时间复杂度为O(M*L),其中M是words数组的长度,L是单词的平均长度。
- 因此,整体的时间复杂度为O(NML)。
空间复杂度:
- 需要使用一个哈希表来存储words数组中每个单词的出现次数,以及临时变量存储计数信息。哈希表的大小取决于words数组的长度M。
- 此外,还需要一个结果列表来存储符合条件的起始索引。
- 因此,整体的空间复杂度为O(M)。
LeetCode运行结果:
方法二:哈希表和双指针
除了使用滑动窗口的方法外,还可以使用基于哈希表和双指针的解决方案。
这个解决方案使用了双指针的方法。
- 首先,统计words数组中每个单词的出现次数,并存储在wordCount中。
- 然后,通过遍历字符串s的所有可能起始位置,将左边界left初始化为当前起始位置。在每次循环中,使用右指针left + wordLength获取一个单词,并在哈希表tempCount中查找该单词是否存在且次数大于零。如果满足条件,则更新哈希表和计数,并将左边界右移一个单词长度。如果不满足条件,则结束循环。
- 最后,如果计数等于0,则表示窗口内的单词都符合要求,将起始位置添加到结果列表中。
import java.util.*;
class Solution {
public List<Integer> findSubstring(String s, String[] words) {
List<Integer> result = new ArrayList<>();
if (s == null || s.length() == 0 || words == null || words.length == 0) {
return result;
}
int wordLength = words[0].length();
int totalLength = words.length * wordLength;
Map<String, Integer> wordCount = new HashMap<>();
for (String word : words) {
wordCount.put(word, wordCount.getOrDefault(word, 0) + 1);
}
for (int i = 0; i <= s.length() - totalLength; i++) {
Map<String, Integer> tempCount = new HashMap<>(wordCount);
int count = words.length;
int left = i;
while (count > 0) {
String word = s.substring(left, left + wordLength);
if (tempCount.containsKey(word) && tempCount.get(word) > 0) {
tempCount.put(word, tempCount.get(word) - 1);
count--;
left += wordLength;
} else {
break;
}
}
if (count == 0) {
result.add(i);
}
}
return result;
}
}
复杂度分析:
时间复杂度:
- 首先,需要遍历字符串s的所有可能起始位置,此操作的时间复杂度为O(N),其中N是s的长度。
- 在每个起始位置,需要通过双指针循环遍历,直到窗口内的单词数量等于words数组的长度。由于窗口长度为words数组的长度乘以单词的长度,因此该操作的时间复杂度为O(L * M),其中L是单词的平均长度,M是words数组的长度。
- 因此,整体的时间复杂度为O(N * L * M)。
空间复杂度:
- 需要使用一个哈希表wordCount来存储words数组中每个单词的出现次数,该哈希表大小最多为words数组的长度M。
- 此外,还需要使用一个哈希表tempCount来存储临时的单词计数信息,该哈希表的大小也为M。
- 因此,整体的空间复杂度为O(M)。
综上所述,该基于哈希表和双指针的解决方案的时间复杂度为O(N * L * M),空间复杂度为O(M)。与滑动窗口的方法相比,其时间复杂度稍高,但实际运行效果可能会因具体情况而有所不同。
LeetCode运行结果:

方法三:动态规划
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
public class Solution {
public List<Integer> findSubstring(String s, String[] words) {
List<Integer> result = new ArrayList<>();
if (s == null || s.length() == 0 || words == null || words.length == 0) {
return result;
}
int wordLen = words[0].length();
int wordCount = words.length;
int windowLen = wordLen * wordCount;
Map<String, Integer> wordCountMap = new HashMap<>();
for (String word : words) {
wordCountMap.put(word, wordCountMap.getOrDefault(word, 0) + 1);
}
for (int i = 0; i < s.length() - windowLen + 1; i++) {
Map<String, Integer> tempCountMap = new HashMap<>(wordCountMap);
for (int j = 0; j < wordCount; j++) {
String word = s.substring(i + j * wordLen, i + (j + 1) * wordLen);
if (!tempCountMap.containsKey(word)) {
break;
}
tempCountMap.put(word, tempCountMap.get(word) - 1);
if (tempCountMap.get(word) == 0) {
tempCountMap.remove(word);
}
if (tempCountMap.isEmpty()) {
result.add(i);
break;
}
}
}
return result;
}
}
这段代码使用了一个wordCountMap哈希表来记录words数组中每个单词出现的次数。然后,通过两个嵌套的循环遍历字符串s,在每个位置检查以该位置为起点的子串是否包含words数组中的所有单词。
其中,外层循环遍历了所有可能的起始位置,内层循环遍历了窗口内的所有单词。在内层循环中,使用tempCountMap记录当前窗口内各个单词的剩余次数,同时进行相应的更新和判断操作。当tempCountMap为空时,表示窗口内包含了words数组中的所有单词,将该起始位置加入结果列表。
最后,返回结果列表即可。
复杂度分析:
- 时间复杂度:假设字符串s的长度为n,words数组中单词的平均长度为m,words数组的长度为k。构建wordCountMap的时间复杂度为O(k),外层循环需要遍历长度为(n-windowLen+1)的窗口,其中windowLen为wordLen * wordCount,因此外层循环的时间复杂度为O(n)。内层循环遍历窗口内的所有单词,单次循环操作的时间复杂度为O(m),内层循环的总时间复杂度为O(wordCount * m)。因此,整体时间复杂度为O(n * k * m)。
- 空间复杂度:构建wordCountMap和tempCountMap时使用了两个哈希表,每个哈希表的大小取决于words数组的长度,因此空间复杂度为O(k)。
总结起来,该动态规划解决方案的时间复杂度为O(n * k * m),空间复杂度为O(k)。其中,n为字符串s的长度,k为words数组的长度,m为单词的平均长度。
LeetCode运行结果:
第二题
题目来源
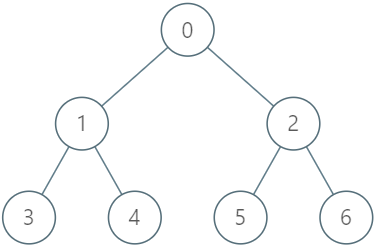
1993. 树上的操作 - 力扣(LeetCode)
题目内容


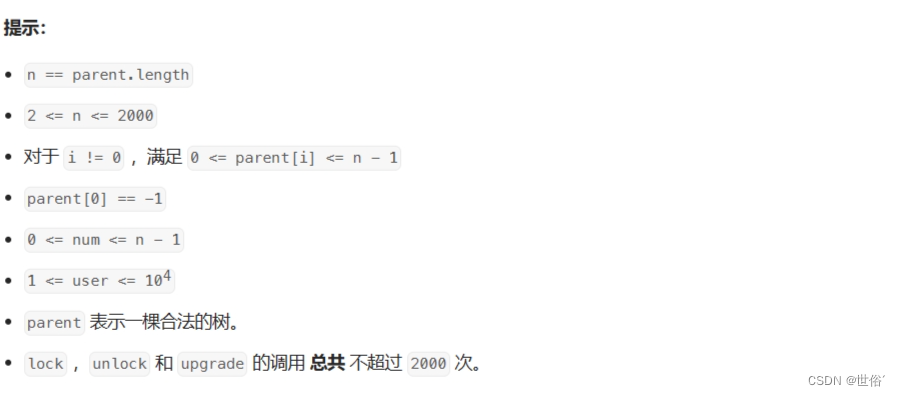
解决方法
方法一:深度优先搜索(DFS)
使用深度优先搜索(DFS)来实现 LockingTree 类。可以通过递归地遍历树的节点来判断锁的状态,以及执行相应的锁定、解锁和升级操作。
具体思路如下:
- 使用一个数组 parent 来表示树的父节点关系。
- 使用哈希表 locks 来保存节点的锁状态,其中键为节点编号,值为锁住该节点的用户编号。
- 使用哈希表 children 来保存每个节点的孩子节点列表。
- 在 lock() 方法中,判断给定节点是否已经上锁,如果未上锁则将其加锁,并返回 true;否则返回 false。
- 在 unlock() 方法中,判断给定节点是否已经被指定用户锁住,如果是则解锁,并返回 true;否则返回 false。
- 在 upgrade() 方法中,首先判断给定节点是否未上锁、有上锁的子孙节点以及没有任何上锁的祖先节点。如果满足条件,则将该节点上锁,并解锁所有子孙节点,然后返回 true;否则返回 false。
- 为了判断是否有上锁的子孙节点,可以使用递归函数 hasLockedDescendant() 来遍历给定节点的子孙节点。如果找到任何一个上锁节点,则返回 true;否则返回 false。
- 为了判断是否有上锁的祖先节点,可以使用迭代函数 hasLockedAncestor() 来遍历给定节点的父节点链。如果找到任何一个上锁节点,则返回 true;否则返回 false。
- 为了解锁给定节点的所有子孙节点,可以使用递归函数 unlockDescendants() 来遍历给定节点的子孙节点,并解锁它们。
- 在构造函数中,根据父节点关系构建每个节点的孩子节点列表。
- 上述步骤完成后,即可实现 LockingTree 类的相关操作。
import java.util.*;
class LockingTree {
private int[] parent;
private Map<Integer, Integer> locks;
private Map<Integer, List<Integer>> children;
public LockingTree(int[] parent) {
this.parent = parent;
this.locks = new HashMap<>();
this.children = new HashMap<>();
for (int i = 0; i < parent.length; i++) {
children.put(i, new ArrayList<>());
}
// 构建树的孩子列表
for (int i = 1; i < parent.length; i++) {
children.get(parent[i]).add(i);
}
}
public boolean lock(int num, int user) {
if (!locks.containsKey(num)) {
locks.put(num, user);
return true;
} else {
return false;
}
}
public boolean unlock(int num, int user) {
if (locks.containsKey(num) && locks.get(num) == user) {
locks.remove(num);
return true;
} else {
return false;
}
}
public boolean upgrade(int num, int user) {
if (!locks.containsKey(num) && hasLockedDescendant(num) && !hasLockedAncestor(num)) {
locks.put(num, user);
unlockDescendants(num);
return true;
} else {
return false;
}
}
private boolean hasLockedDescendant(int num) {
for (int child : children.get(num)) {
if (locks.containsKey(child) || hasLockedDescendant(child)) {
return true;
}
}
return false;
}
private boolean hasLockedAncestor(int num) {
int curr = parent[num];
while (curr != -1) {
if (locks.containsKey(curr)) {
return true;
}
curr = parent[curr];
}
return false;
}
private void unlockDescendants(int num) {
for (int child : children.get(num)) {
locks.remove(child);
unlockDescendants(child);
}
}
}
复杂度分析:
时间复杂度:
- 构造函数的时间复杂度为 O(n),其中 n 表示节点数目。需要遍历父节点数组构建每个节点的孩子节点列表。
- lock() 方法的时间复杂度为 O(1)。只需在哈希表中执行一次插入操作。
- unlock() 方法的时间复杂度为 O(1)。只需在哈希表中执行一次删除操作。
- upgrade() 方法的时间复杂度为 O(h + s),其中 h 表示树的高度,s 表示子孙节点数目。需要判断给定节点是否未上锁、是否存在上锁的子孙节点以及是否存在上锁的祖先节点。遍历给定节点的子孙节点时间复杂度为 O(s),遍历给定节点的父节点链时间复杂度为 O(h)。
- hasLockedDescendant() 方法的时间复杂度为 O(s),其中 s 表示子孙节点数目。需要递归判断给定节点的子孙节点是否被上锁。
- hasLockedAncestor() 方法的时间复杂度为 O(h),其中 h 表示树的高度。需要迭代判断给定节点的父节点链中是否存在已上锁的节点。
- unlockDescendants() 方法的时间复杂度为 O(s),其中 s 表示子孙节点数目。需要递归解锁给定节点的所有子孙节点。
空间复杂度:
- 构造函数的空间复杂度为 O(n),需要存储每个节点以及其对应的孩子节点列表。
- lock() 方法和 unlock() 方法的空间复杂度为 O(1),只需在哈希表中存储节点的上锁状态。
- upgrade() 方法的空间复杂度为 O(h),需要存储给定节点的父节点链。
- hasLockedDescendant() 方法的空间复杂度为 O(s),其中 s 表示子孙节点数目。递归调用时会使用函数调用栈来保存递归的上下文信息。
- hasLockedAncestor() 方法的空间复杂度为 O(1),不需要额外的空间。
- unlockDescendants() 方法的空间复杂度为 O(s),其中 s 表示子孙节点数目。递归调用时会使用函数调用栈来保存递归的上下文信息。
综上所述,整个 LockingTree 类的时间复杂度主要取决于构造函数的 O(n)、upgrade() 方法的 O(h + s) 和 hasLockedDescendant() 方法的 O(s)。空间复杂度主要取决于构造函数的 O(n) 和 upgrade() 方法的 O(h)。在一般情况下,树的高度 h 相对于节点数目 n 和子孙节点数目 s 较小。
因此,整体的时间复杂度为 O(n),空间复杂度为 O(n)。
LeetCode运行结果:

方法二:树结构
class LockingTree {
public LockingTree(int[] parent) {
int n = parent.length;
this.parent = parent;
lockUser = new int[n];
map = new HashMap<>();
for(int i = -1; i < n; i++){map.put(i,new HashSet<>());}
for(int i = 0; i < n; i++){map.get(parent[i]).add(i);}// 把当前节点放到对应的父节点里面
}
int[] parent;
int[] lockUser;
Map<Integer,Set<Integer>> map;
public boolean lock(int num, int user) {
if(lockUser[num] == 0){
lockUser[num] = user;
return true;
}
return false;
}
public boolean unlock(int num, int user) {
if(lockUser[num] == user){
lockUser[num] = 0;
return true;
}
return false;
}
public boolean upgrade(int num, int user) {
// 判断本身是否上锁
if (lockUser[num] != 0) {
return false;
}
// 判断祖先结点是否上锁
int find = parent[num];
while (find != -1) {
if (lockUser[find] != 0) {
return false;
}
find = parent[find];
}
// 判断是否有子孙节点上锁并解锁
if (hasLockedDescendants(num)) {
unlockDescendants(num);
lockUser[num] = user;
return true;
} else {
return false;
}
}
private boolean hasLockedDescendants(int num) {
for (int child : map.get(num)) {
if (lockUser[child] != 0 || hasLockedDescendants(child)) {
return true;
}
}
return false;
}
private void unlockDescendants(int num) {
for (int child : map.get(num)) {
if (lockUser[child] != 0) {
lockUser[child] = 0;
}
unlockDescendants(child);
}
}
}
这段代码实现的是一个锁定树的类 LockingTree,其中的思路如下:
- 构造函数 LockingTree(int[] parent):接收一个父节点数组,表示树的结构。在构造函数中,首先初始化一些变量,包括父节点数组、每个节点的锁定用户数组和节点与子节点的映射关系。然后,遍历父节点数组,将每个节点放入对应父节点的子节点集合。
- 锁定节点方法 lock(int num, int user):接收一个节点编号和用户编号,用于将指定节点锁定给指定用户。在该方法中,首先判断该节点是否已被锁定,如果未被锁定,则将其锁定给指定用户并返回 true,表示成功锁定;如果已被锁定,则返回 false,表示锁定失败。
- 解锁节点方法 unlock(int num, int user):接收一个节点编号和用户编号,用于解除指定节点的锁定状态。在该方法中,首先判断该节点是否由指定用户锁定,如果是则解除锁定并返回 true,表示成功解锁;如果不是,则返回 false,表示解锁失败。
- 升级节点方法 upgrade(int num, int user):接收一个节点编号和用户编号,用于升级指定节点的锁定状态。在该方法中,首先判断该节点是否已被锁定,如果是则返回 false,表示升级失败;然后,逐级判断该节点的祖先节点是否有被锁定的节点,如果有则返回 false,表示升级失败;接着,判断该节点的子孙节点是否有被锁定的节点,如果有,则解锁所有子孙节点并将当前节点锁定给指定用户,并返回 true,表示升级成功;如果没有,则返回 false,表示升级失败。
- 辅助方法 hasLockedDescendants(int num):递归地检查某个节点的子孙节点中是否有被锁定的节点。在该方法中,首先遍历该节点的所有子节点,如果有子节点已被锁定,或者子节点的子孙节点中有被锁定的节点,则返回 true,表示存在已被锁定的节点;如果遍历完所有子节点,都没有找到已被锁定的节点,则返回 false,表示没有已被锁定的节点。
- 辅助方法 unlockDescendants(int num):递归地解锁某个节点的所有子孙节点。在该方法中,首先遍历该节点的所有子节点,如果子节点已被锁定,则解除锁定;然后,递归调用该方法,解锁子节点的所有子孙节点。
总体来说,这段代码通过维护一个树结构和相关的数据结构数组,实现了对树中节点的锁定、解锁和升级操作。其中,锁定节点时需要考虑节点的锁定状态以及祖先节点和子孙节点的锁定情况。解锁节点时需要判断节点的锁定用户是否为当前用户。升级节点时需要判断节点的锁定状态、祖先节点的锁定状态以及子孙节点的锁定状态,并进行相应的操作。
复杂度分析:
- 构造函数 LockingTree(int[] parent):遍历父节点数组,构建树结构和相关数据结构数组。时间复杂度为 O(N),其中 N 是节点的数量。
- 锁定节点方法 lock(int num, int user):检查节点的锁定状态并锁定节点。时间复杂度为 O(1)。
- 解锁节点方法 unlock(int num, int user):检查节点的锁定状态并解锁节点。时间复杂度为 O(1)。
- 升级节点方法 upgrade(int num, int user):检查节点的锁定状态、祖先节点的锁定状态以及子孙节点的锁定状态,并进行相应操作。最坏情况下,需要递归遍历所有的子孙节点,时间复杂度为 O(N)。
- 辅助方法 hasLockedDescendants(int num):递归地检查某个节点的子孙节点中是否有被锁定的节点。最坏情况下,需要遍历所有的子孙节点,时间复杂度为 O(N)。
- 辅助方法 unlockDescendants(int num):递归地解锁某个节点的所有子孙节点。最坏情况下,需要遍历所有的子孙节点,时间复杂度为 O(N)。
总体来说,构造函数的时间复杂度为 O(N),其他方法的时间复杂度大多为 O(1),只有在遍历节点时需要递归,时间复杂度为 O(N)。空间复杂度方面,需要额外存储树结构、父节点数组和每个节点的锁定用户数组,因此为 O(N)。
LeetCode运行结果:

第三题
题目来源
31. 下一个排列 - 力扣(LeetCode)
题目内容

解决方法
方法一:遍历交换
我们可以使用以下步骤来找到给定数组的下一个排列:
- 从右往左遍历数组,找到第一个下降的元素,记为 i。即找到满足 nums[i] < nums[i+1] 的最大下标 i。
- 如果找不到这样的 i,说明整个数组是降序的,即不存在下一个更大的排列。此时,将整个数组翻转,得到字典序最小的排列。
- 如果找到了 i,再次从右往左遍历数组,找到第一个大于 nums[i] 的元素,记为 j。即找到满足 nums[j] > nums[i] 的最大下标 j。
- 交换 nums[i] 和 nums[j]。
- 将位置 i 后面的元素按升序排列,以得到字典序最小的排列。
- 通过以上步骤,我们可以在原地修改给定数组,得到下一个排列。
public class Solution {
public void nextPermutation(int[] nums) {
int n = nums.length;
// 从后向前找到第一个升序的位置 i
int i = n - 2;
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
// 在位置 i 后面找到刚好大于 nums[i] 的元素,并交换它们
int j = n - 1;
while (j > i && nums[j] <= nums[i]) {
j--;
}
swap(nums, i, j);
}
// 将 i 后面的元素按升序排列,以得到字典序最小的排列
reverse(nums, i + 1, n - 1);
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
private void reverse(int[] nums, int start, int end) {
while (start < end) {
swap(nums, start, end);
start++;
end--;
}
}
}
复杂度分析:
- 时间复杂度:O(n),其中 n 是数组的长度。我们需要从右往左遍历数组找到第一个下降的元素,这一步最坏情况下需要遍历整个数组。然后,我们需要再次从右往左遍历数组找到第一个大于 nums[i] 的元素。接下来,在位置 i 后面进行元素的升序排列,这一步也需要 O(n) 的时间复杂度。因此,总体上,算法的时间复杂度是 O(n)。
- 空间复杂度:O(1)。算法只需要使用常数个额外的变量,所以空间复杂度是 O(1)。
LeetCode运行结果:

方法二:递归
以下是该方法的详细步骤:
- 从右往左找到第一个满足 nums[i] < nums[i+1] 的元素下标 i。如果找不到这样的 i,则说明整个数组是降序的,不存在下一个更大的排列。直接将整个数组进行翻转,得到字典序最小的排列,算法结束。
- 在位置 i 后面的子数组中,找到大于 nums[i] 且最接近的元素下标 j。
- 交换 nums[i] 和 nums[j]。
- 对位置 i 后面的子数组进行递归调用,将其进行升序排序。
- 通过以上步骤,我们可以得到给定数组的下一个排列。
public class Solution {
public void nextPermutation(int[] nums) {
int n = nums.length;
int i = n - 2;
// 找到第一个满足 nums[i] < nums[i+1] 的元素下标 i
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
// 在位置 i 后面的子数组中,找到大于 nums[i] 且最接近的元素下标 j
int j = findNextGreater(nums, i);
// 交换 nums[i] 和 nums[j]
swap(nums, i, j);
}
// 对位置 i 后面的子数组进行递归调用,将其进行升序排序
reverse(nums, i + 1, n - 1);
}
private int findNextGreater(int[] nums, int start) {
int target = nums[start];
int nextGreater = start + 1;
while (nextGreater < nums.length && nums[nextGreater] > target) {
nextGreater++;
}
return nextGreater - 1;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
private void reverse(int[] nums, int start, int end) {
while (start < end) {
swap(nums, start, end);
start++;
end--;
}
}
}
复杂度分析:
- 时间复杂度:在最坏情况下,需要遍历整个数组找到位置 i,并在位置 i 之后的子数组中查找元素 j,所以时间复杂度为 O(n)。并且递归调用函数
reverse需要对位置 i 后面的子数组进行升序排序,其时间复杂度为 O(n)。因此,总的时间复杂度为 O(n+n) = O(n)。 - 空间复杂度:除了输入数组以外,在递归调用的过程中不需要额外的空间,所以空间复杂度为 O(1)。
LeetCode运行结果:

方法三:字典序法
可以使用字典序法来找到给定数组的下一个排列。
以下是字典序法的实现步骤:
- 从右往左找到第一个满足 nums[i] < nums[i+1] 的元素下标 i。如果找不到这样的 i,则说明整个数组是降序的,不存在下一个更大的排列。直接将整个数组进行翻转,得到字典序最小的排列,算法结束。
- 从右往左找到第一个大于 nums[i] 的元素下标 j。
- 交换 nums[i] 和 nums[j]。
- 将位置 i 后面的子数组按升序排列。
通过以上步骤,我们可以得到给定数组的下一个排列。
public class Solution {
public void nextPermutation(int[] nums) {
int n = nums.length;
int i = n - 2;
// 找到第一个满足 nums[i] < nums[i+1] 的元素下标 i
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
// 从右往左找到第一个大于 nums[i] 的元素下标 j
int j = n - 1;
while (j >= 0 && nums[j] <= nums[i]) {
j--;
}
// 交换 nums[i] 和 nums[j]
swap(nums, i, j);
}
// 将位置 i 后面的子数组按升序排列
Arrays.sort(nums, i + 1, n);
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
复杂度分析:
时间复杂度:
- 寻找第一个满足 nums[i] < nums[i+1] 的元素下标 i 的过程需要遍历整个数组,时间复杂度为 O(n)。
- 从右往左找到第一个大于 nums[i] 的元素下标 j 的过程最坏情况下需要遍历整个数组,时间复杂度也为 O(n)。
- 交换 nums[i] 和 nums[j] 只是一次简单的元素交换,时间复杂度为 O(1)。
- 将位置 i 后面的子数组按升序排列的过程使用了 Arrays.sort() 方法,其时间复杂度为 O(mlogm),其中 m 是子数组的长度,因为只对部分数组进行排序,所以这里的时间复杂度可以近似为 O(n)。
- 综上所述,算法的总体时间复杂度为 O(n)。
空间复杂度:
- 算法只使用了常数级别的额外空间,故空间复杂度为 O(1)。
LeetCode运行结果: