目录

题目：

示例：

分析：

代码：

---

题目：

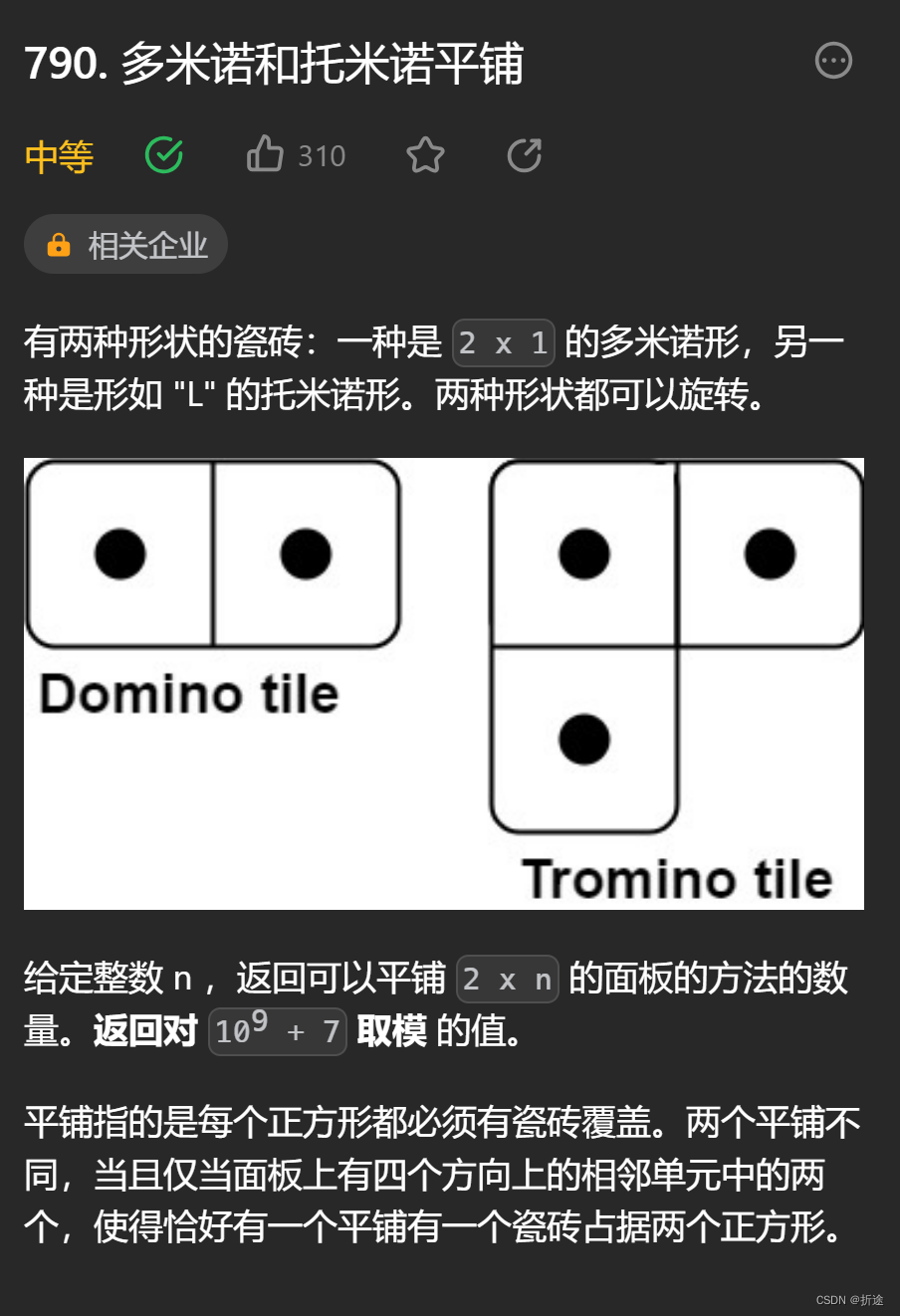
示例：

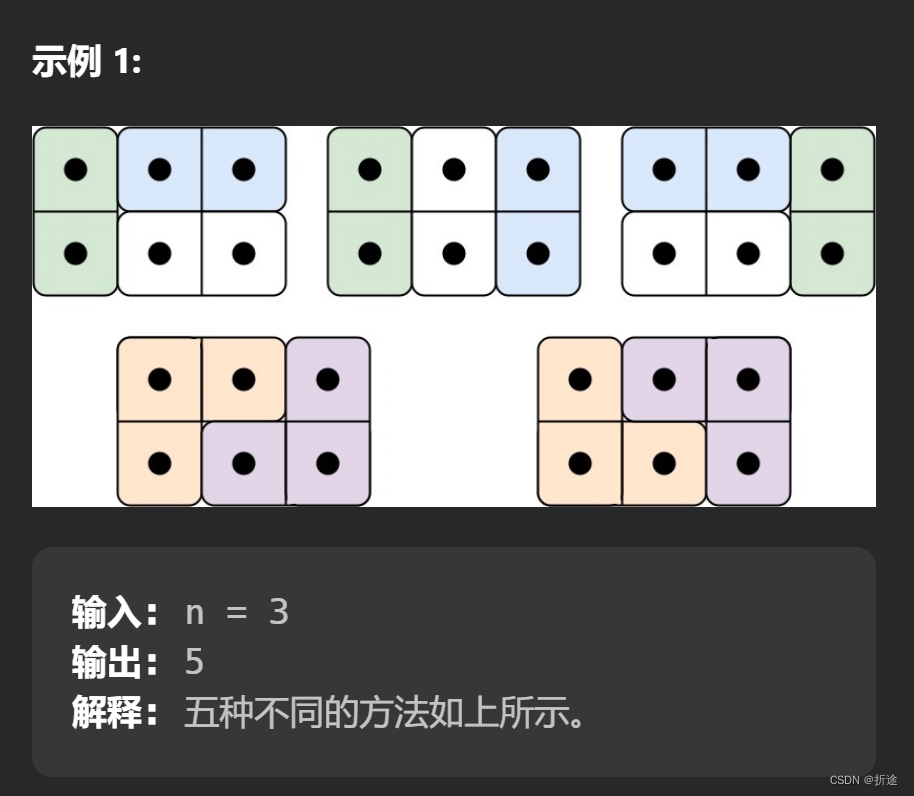
分析：

题目给我一个数字n，表示我们有2*n大小的地板需要铺。

我们拥有两种瓷砖，一种的长度为2的多米诺，另一种是长度为3，但是是“L”形的托米诺。

问我们有多少种平铺方案。

那么这道题很明显是一道动态规划题，不过递推公式不太好找，我们可以画一下图来慢慢试试能不能推导出来。

当n=1的时候，我们只能用一个多米诺来平铺，也就只有一种方案：

n=2时，有两种方案：

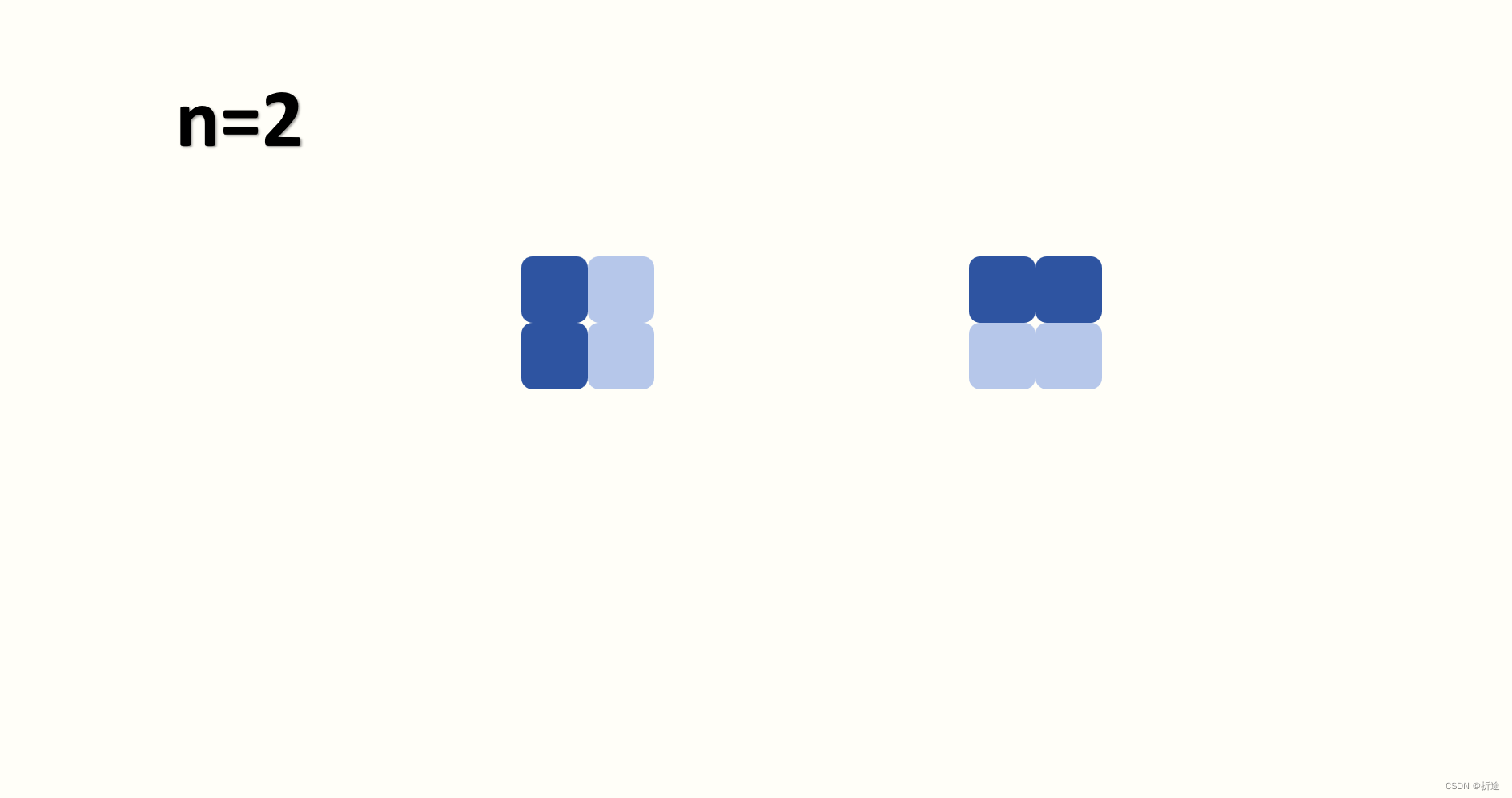
n=3时，有五种方案：

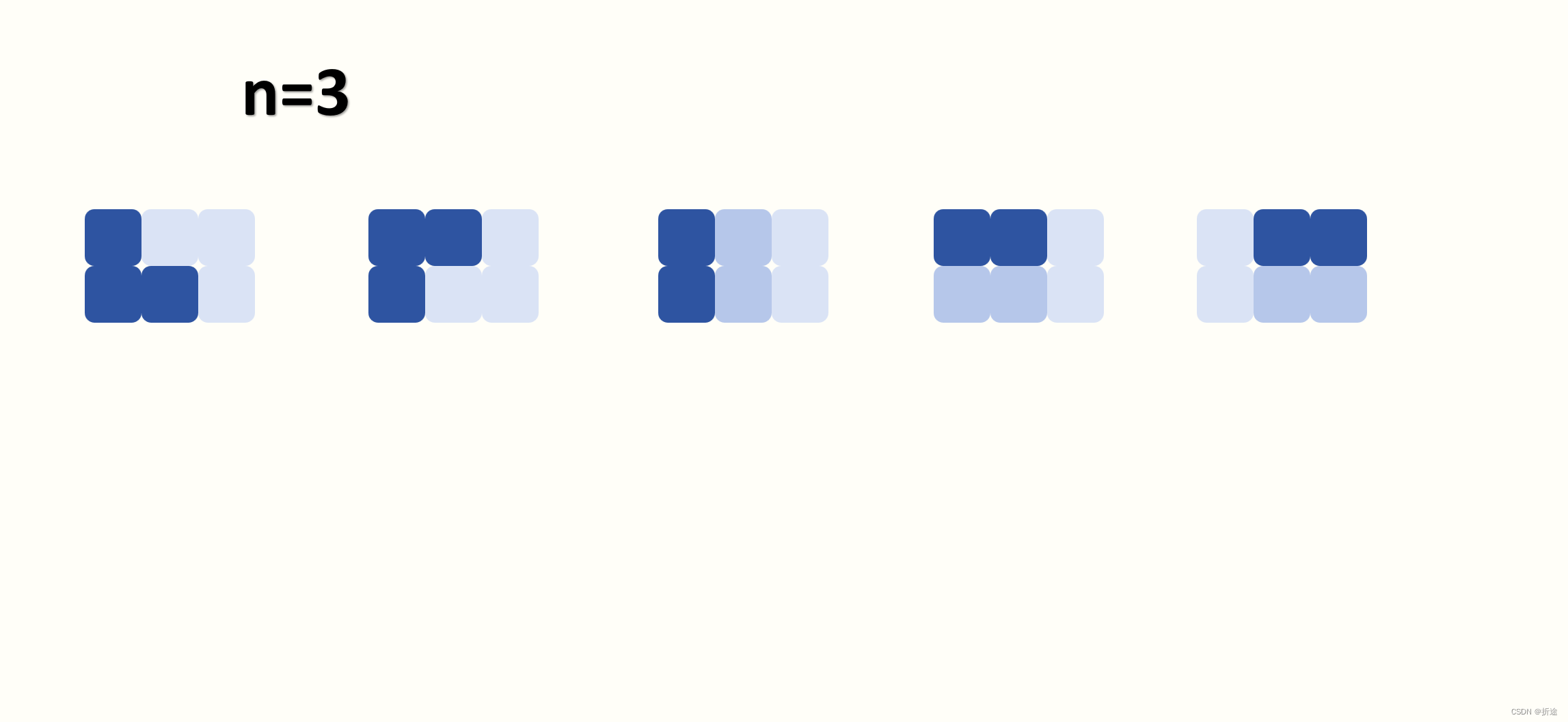
 n=4时，有十一种方案：

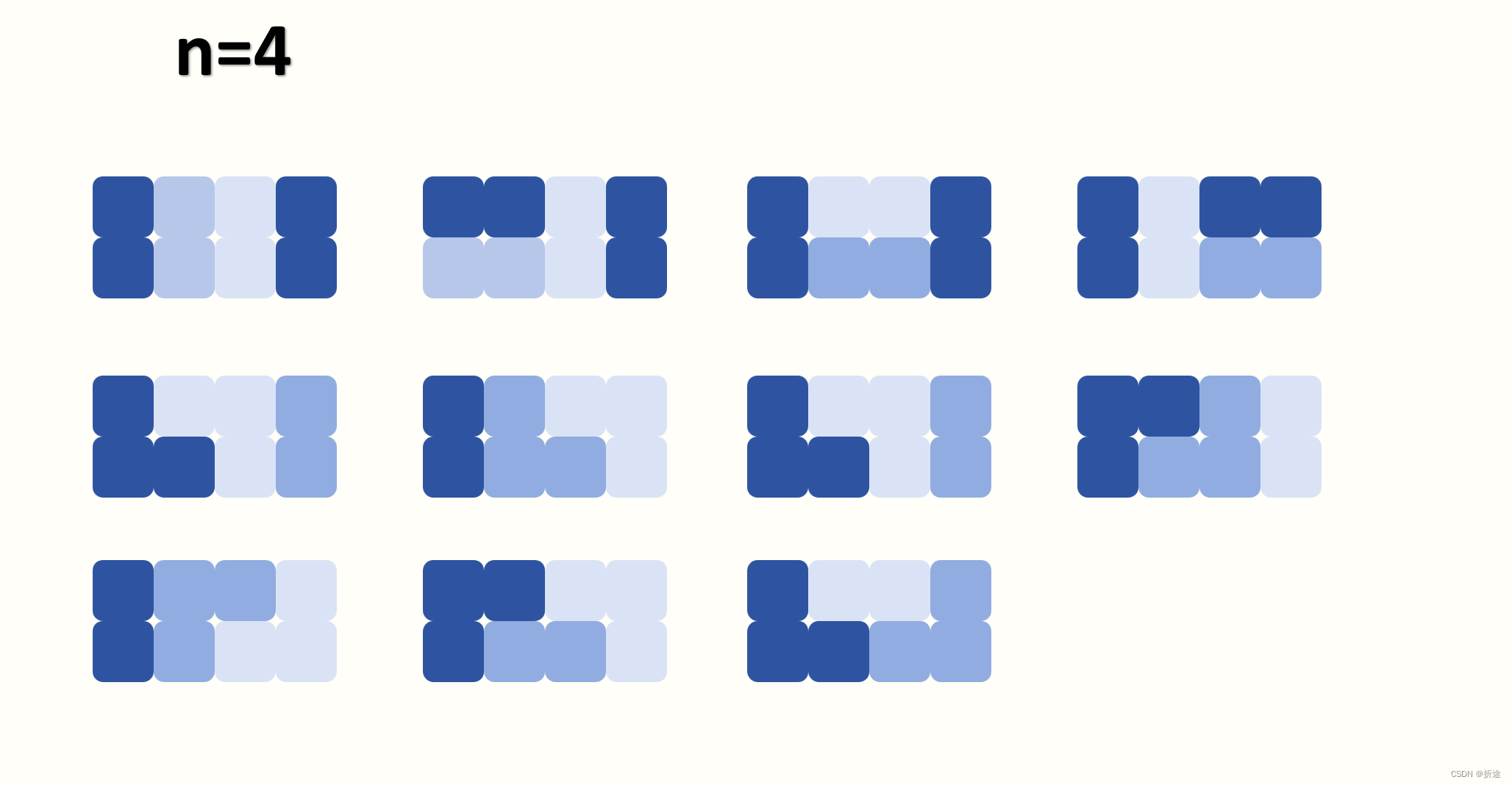
 一般来说，样本数量有个3，4个就差不多了，我们凑了四个，可以开始推断猜测了。

因为托米诺有一些特殊，它只能和托米诺配合才可以填满矩阵，也就是说不管n是多少，方案里的托米诺的数量一定是偶数的。

也就是说n=1和n=2时的方案是没什么参考性的，我们直接看n=3和n=4时的方案。

我们先看n=3时的方案：

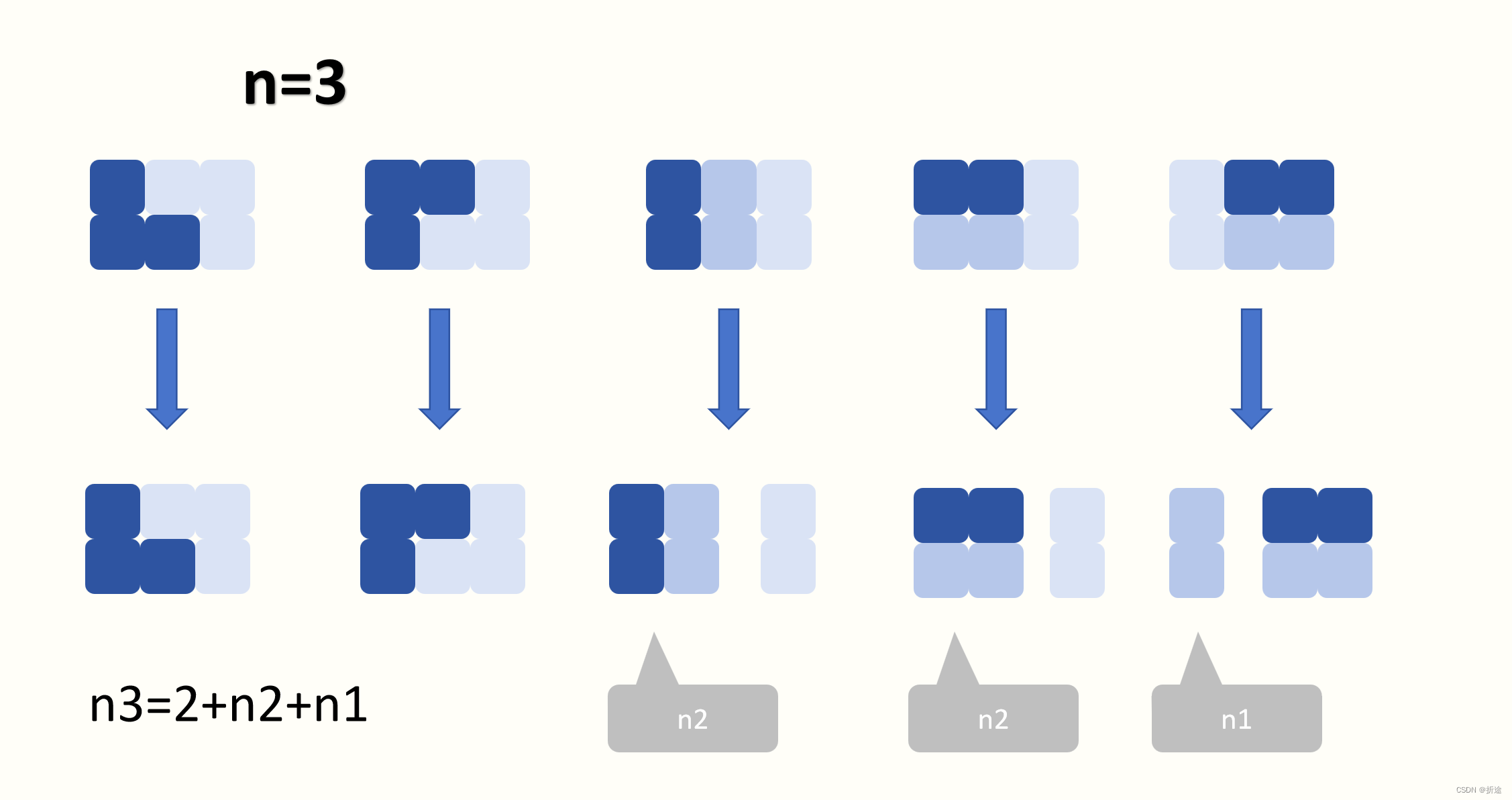
 除了两个开头有点奇怪的方案，其他的都是n=2时的方案加一块多米诺，或者是n=1时的方案加两块多米诺。

接着再看看n=4时的方案：

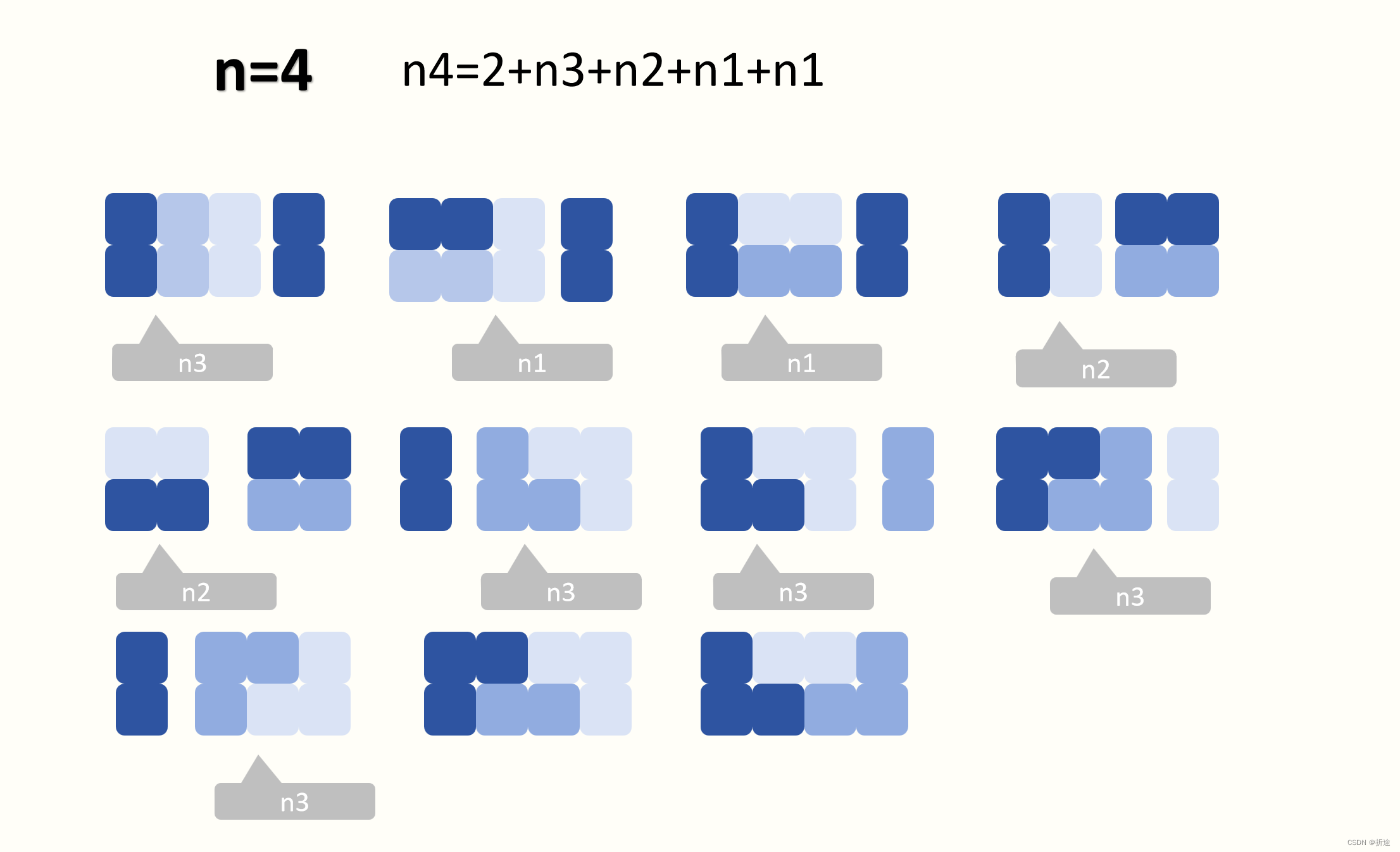
 n=4也是差不多的情况，除了两块奇奇怪怪的方案。其他都是n=3，n=2，n=1时的延伸，而且n=1时的延伸有两种。

那么有一点点的感觉了，我们再大胆推测n=5时的方案（因为有点多，画起来得花好久，就不一一画出了）

 我们压缩一下，发现n=5时也是可以由前面几种方案延伸出来的，并且同样是有两个奇怪的方案无法由其他情况的方案延伸出来。

至此我们就发现出了规律：

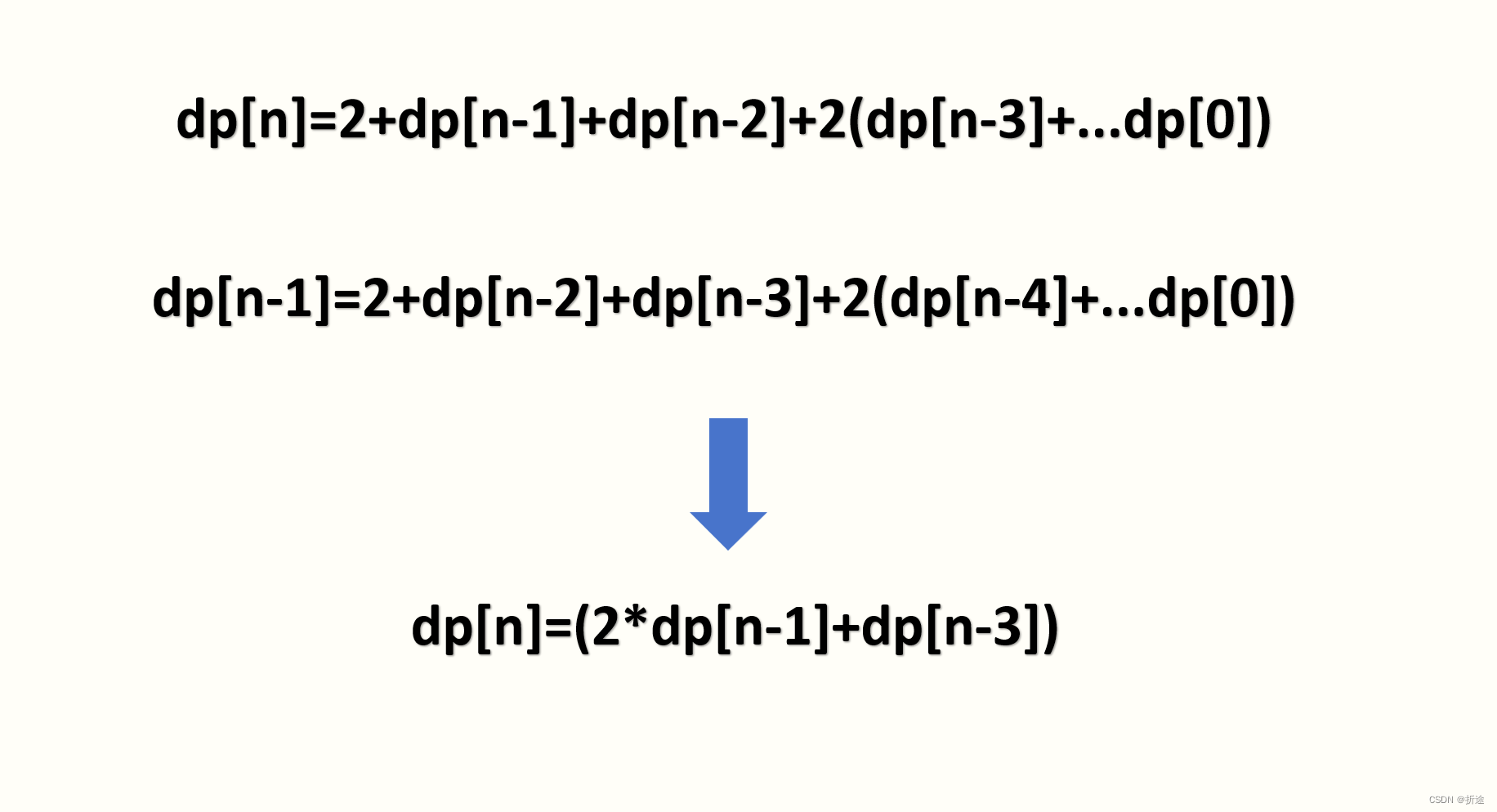
而这也是我们的递推公式，知道递推公式之后，我们只需要初始化dp的前3项，然后开始递推，最终返回最后一个元素即可。

代码：

class Solution {
public:
    int numTilings(int n) {
        vector<long>dp(max(4,n+1),1);
        dp[2]=2;dp[3]=5;
        for(int i=4;i<=n;i++){
            dp[i]=(2*dp[i-1]+dp[i-3])%(1000000007);
        }
        return dp[n];
    }
};