目录
- 发射端模型假设
- 接收端模型假设
- 时延估计(时间跟踪)
- 频偏估计(频率跟踪)
在OFDM系统中,为了估计出信号传输遇到的时间偏移和频率偏移,可以采用导频进行估计。
发射端模型假设
我们假设如下模型:
一个时隙有14个ofdm符号,每个符号有1024个子载波。
其中792个子载波是数据子载波,232个子载波是空载波。
其中OFDM3和OFDM13的792个子载波中含有dmrs导频符号(频域)。
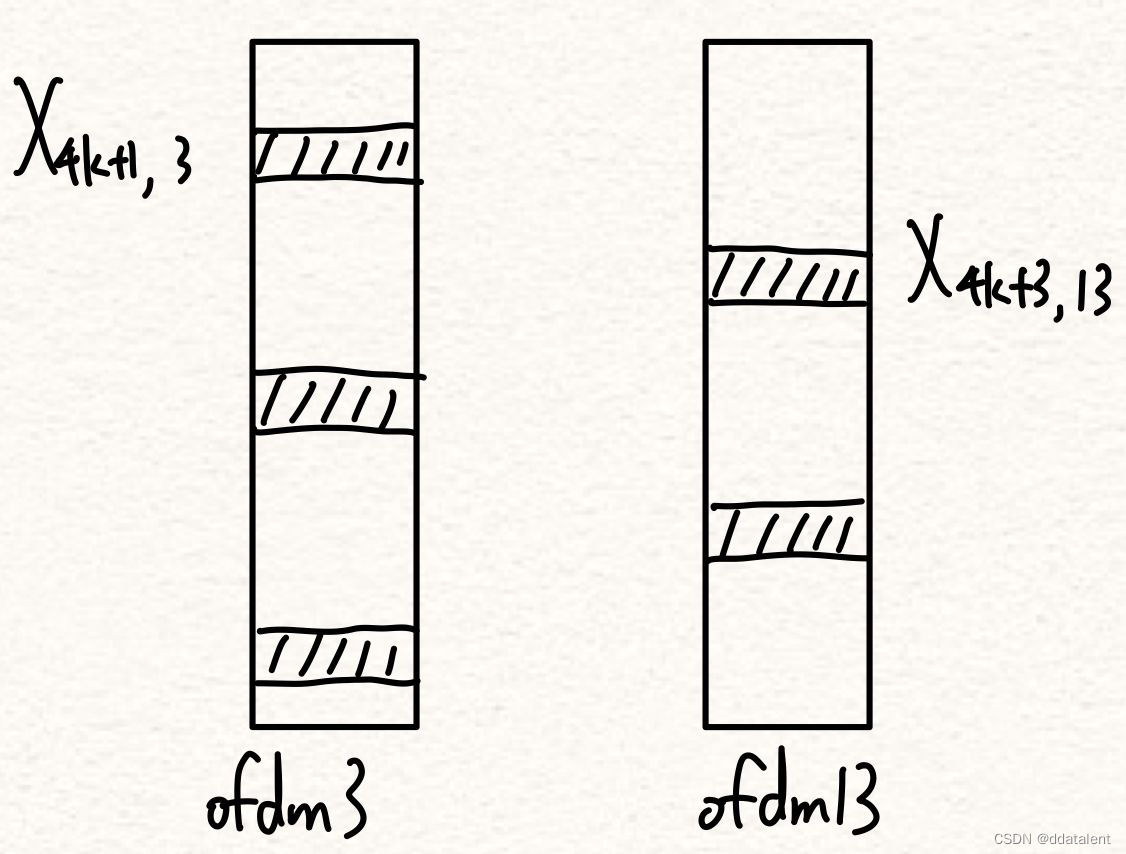
X 4 k + 1 , 3 表示 o f d m 3 中导频位置为第 4 k + 1 个子载波, k = 0 − 197 X_{4k+1,3}表示ofdm3中导频位置为第4k+1个子载波,k=0 - 197 X4k+1,3表示ofdm3中导频位置为第4k+1个子载波,k=0−197 X 4 k + 3 , 13 表示 o f d m 13 中导频位置为第 4 k + 3 个子载波, k = 0 − 197 X_{4k+3,13}表示ofdm13中导频位置为第4k+3个子载波,k=0 - 197 X4k+3,13表示ofdm13中导频位置为第4k+3个子载波,k=0−197
构建发射端模型为:
x
n
,
M
=
1
N
∑
k
=
−
512
511
X
k
,
M
e
j
2
π
n
k
N
,
n
=
1
−
1024
x_{n,M} = \frac{1}{N} \sum_{k=-512}^{511} X_{k,M} e^{j\frac{2\pi nk}{N}} , n=1-1024
xn,M=N1k=−512∑511Xk,MejN2πnk,n=1−1024
x
n
,
M
x_{n,M}
xn,M为时域第M个ofdm符号的第n个码片,
X
k
,
M
X_{k,M}
Xk,M为频域第M个ofdm符号的第k个子载波符号。
经过信道传输后,引入时延
τ
\tau
τ和频偏
f
d
f_d
fd
接收端模型假设
则接收端接收模型可表示为:
y
n
,
M
=
h
⨂
x
n
−
τ
,
M
e
j
2
π
f
d
t
M
+
w
n
,
M
y_{n,M}= h\bigotimes x_{n-\tau,M} e ^{j2\pi f_d t_M} + w_{n,M}
yn,M=h⨂xn−τ,Mej2πfdtM+wn,M
其中,
t
M
t_M
tM表示接收到ofdm M的时间,不妨假设
t
3
=
0
t_3=0
t3=0,
t
13
=
△
t
t_{13}=\bigtriangleup t
t13=△t。
w
n
,
M
w_{n,M}
wn,M表示噪声。
假设信道是时域上不变,频域上变化的。即对于同一个子载波,不同时间的信道响应是相同的。但是同一时间,不同子载波的信道响应不相同。
将上式转换为频域表达式可得
Y
k
,
3
=
H
k
X
k
,
3
e
−
j
2
π
k
N
τ
+
W
k
,
3
Y_{k,3}=H_{k} X_{k,3} e^{-j \frac{2\pi k}{N} \tau} +W_{k,3}
Yk,3=HkXk,3e−jN2πkτ+Wk,3
Y
k
,
13
=
H
k
X
k
,
13
e
−
j
2
π
k
N
τ
e
j
2
π
f
d
△
t
+
W
k
,
13
Y_{k,13}=H_{k} X_{k,13} e^{-j \frac{2\pi k}{N} \tau} e^{j 2\pi f_d \bigtriangleup t}+W_{k,13}
Yk,13=HkXk,13e−jN2πkτej2πfd△t+Wk,13
观察第一个表达式我们可以得知,时延 τ \tau τ产生的相偏影响对于同一个ofdm符号的不同子载波是不同的,但是与时间无关,也就是对每个ofdm符号的影响是相同的。
观察第二个表达式我们可以得知,频偏 f d f_d fd对ofdm系统产生的相偏影响与时间t有关,和子载波k无关。也就是对于不同ofdm符号的影响是不同的,但是对于同一个ofdm符号的不同子载波是相同的
我们的目的就是估计出时延 τ \tau τ和频偏 f d f_d fd
时延估计(时间跟踪)
在已知导频的情况下,我们只需要提取出导频位置的子载波进行如下计算(*表示共轭):
Y
4
k
+
1
,
3
X
4
k
+
1
,
3
∗
=
∣
X
4
k
+
1
,
3
∣
2
H
4
k
+
1
e
−
j
2
π
(
4
k
+
1
)
N
τ
+
W
4
k
+
1
,
3
Y_{4k+1,3}X_{4k+1,3}^* = |X_{4k+1,3}|^2 H_{4k+1} e^{-j \frac{2\pi (4k+1)}{N} \tau}+W_{4k+1,3}
Y4k+1,3X4k+1,3∗=∣X4k+1,3∣2H4k+1e−jN2π(4k+1)τ+W4k+1,3
Y
4
k
+
3
,
13
X
4
k
+
3
,
13
∗
=
∣
X
4
k
+
3
,
13
∣
2
H
4
k
+
3
e
−
j
2
π
(
4
k
+
3
)
N
τ
e
j
2
π
f
d
△
t
+
W
4
k
+
3
,
3
Y_{4k+3,13}X_{4k+3,13}^* = |X_{4k+3,13}|^2 H_{4k+3} e^{-j \frac{2\pi (4k+3)}{N} \tau}e^{j 2\pi f_d \bigtriangleup t}+W_{4k+3,3}
Y4k+3,13X4k+3,13∗=∣X4k+3,13∣2H4k+3e−jN2π(4k+3)τej2πfd△t+W4k+3,3
考虑到ofdm3和ofdm13的导频是正交的,他们所对应的子载波不同,他们不能直接共轭相乘,因此需要做如下步骤假设:
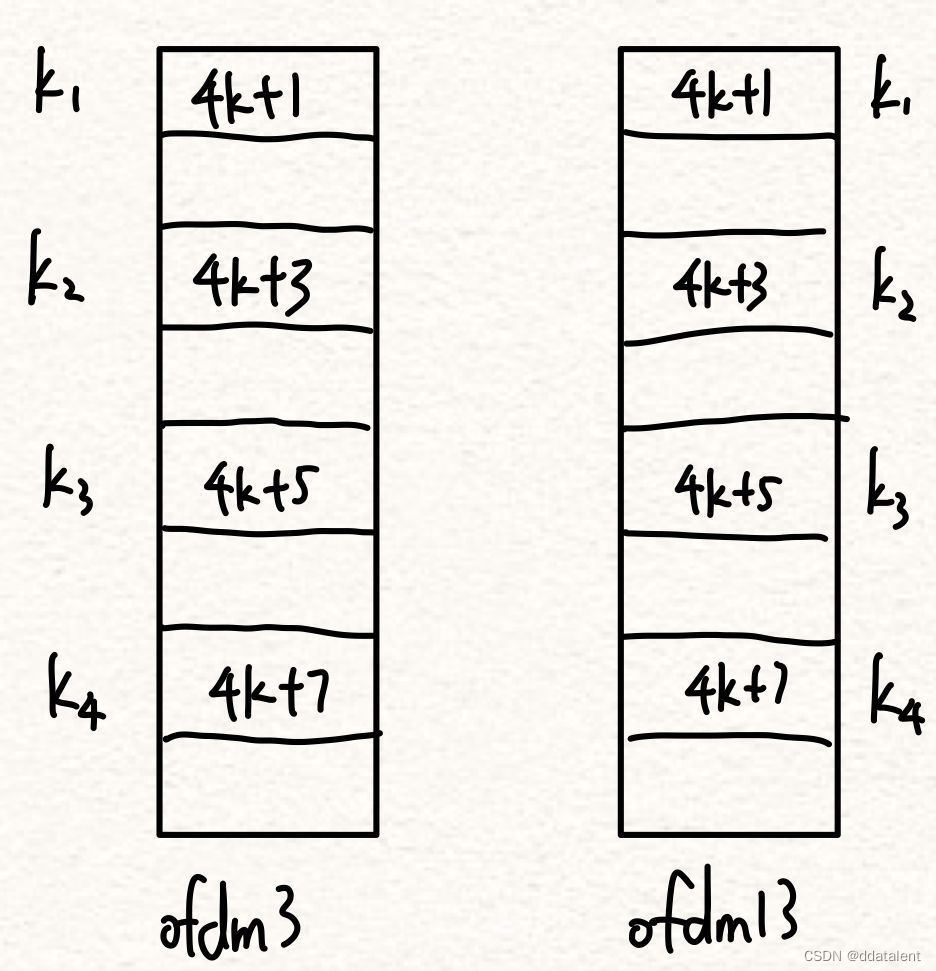
Y k 1 , 3 X k 1 , 3 ∗ = ∣ X k 1 , 3 ∣ 2 H k 1 e − j 2 π k 1 N τ + W k 1 , 3 Y_{k_1,3}X_{k_1,3}^* = |X_{k_1,3}|^2 H_{k_1} e^{-j \frac{2\pi k_1}{N} \tau}+W_{k_1,3} Yk1,3Xk1,3∗=∣Xk1,3∣2Hk1e−jN2πk1τ+Wk1,3 Y k 3 , 3 X k 3 , 3 ∗ = ∣ X k 3 , 3 ∣ 2 H k 3 e − j 2 π k 3 N τ + W k 3 , 3 Y_{k_3,3}X_{k_3,3}^* = |X_{k_3,3}|^2 H_{k_3} e^{-j \frac{2\pi k_3}{N} \tau}+W_{k_3,3} Yk3,3Xk3,3∗=∣Xk3,3∣2Hk3e−jN2πk3τ+Wk3,3 Y k 2 , 13 X k 2 , 13 ∗ = ∣ X k 2 , 13 ∣ 2 H k 2 e − j 2 π k 2 N τ e j 2 π f d △ t + W k 2 , 3 Y_{k_2,13}X_{k_2,13}^* = |X_{k_2,13}|^2 H_{k_2} e^{-j \frac{2\pi k_2}{N} \tau}e^{j 2\pi f_d \bigtriangleup t}+W_{k_2,3} Yk2,13Xk2,13∗=∣Xk2,13∣2Hk2e−jN2πk2τej2πfd△t+Wk2,3 Y k 4 , 13 X k 4 , 13 ∗ = ∣ X k 4 , 13 ∣ 2 H k 4 e − j 2 π k 4 N τ e j 2 π f d △ t + W k 4 , 3 Y_{k_4,13}X_{k_4,13}^* = |X_{k_4,13}|^2 H_{k_4} e^{-j \frac{2\pi k_4}{N} \tau}e^{j 2\pi f_d \bigtriangleup t}+W_{k_4,3} Yk4,13Xk4,13∗=∣Xk4,13∣2Hk4e−jN2πk4τej2πfd△t+Wk4,3
接下来我们令:
(
Y
k
1
,
3
X
k
1
,
3
∗
)
(
Y
k
3
,
3
X
k
3
,
3
∗
)
∗
=
(
∣
X
k
1
,
3
∣
2
H
k
1
e
−
j
2
π
k
1
N
τ
+
W
k
1
,
3
)
(
∣
X
k
3
,
3
∣
2
H
k
3
e
−
j
2
π
k
3
N
τ
+
W
k
3
,
3
)
∗
=
∣
X
k
1
,
3
∣
2
∣
X
k
3
,
3
∣
2
H
k
1
H
k
3
∗
e
−
j
2
π
k
1
N
τ
e
j
2
π
k
3
N
τ
+
W
3
假设信道平坦,我们可以得到
H
k
1
=
H
k
3
,此处
W
3
指代所有的噪声项
=
∣
X
k
1
,
3
∣
2
∣
X
k
3
,
3
∣
2
∣
H
k
1
∣
2
e
j
2
π
(
k
3
−
k
1
)
N
τ
+
W
3
\begin{aligned} (Y_{k_1,3}X_{k_1,3}^*)(Y_{k_3,3}X_{k_3,3}^*)^* &= (|X_{k_1,3}|^2 H_{k_1} e^{-j \frac{2\pi k_1}{N} \tau}+W_{k_1,3})(|X_{k_3,3}|^2 H_{k_3} e^{-j \frac{2\pi k_3}{N} \tau}+W_{k_3,3})^* \\&=|X_{k_1,3}|^2|X_{k_3,3}|^2H_{k_1}H_{k_3}^*e^{-j \frac{2\pi k_1}{N} \tau}e^{j \frac{2\pi k_3}{N} \tau} +W_{3} \\&假设信道平坦,我们可以得到H_{k_1}=H_{k_3},此处W_{3}指代所有的噪声项 \\&=|X_{k_1,3}|^2|X_{k_3,3}|^2|H_{k_1}|^2e^{j \frac{2\pi (k_3 - k_1)}{N} \tau}+W_{3} \end{aligned}
(Yk1,3Xk1,3∗)(Yk3,3Xk3,3∗)∗=(∣Xk1,3∣2Hk1e−jN2πk1τ+Wk1,3)(∣Xk3,3∣2Hk3e−jN2πk3τ+Wk3,3)∗ =∣Xk1,3∣2∣Xk3,3∣2Hk1Hk3∗e−jN2πk1τejN2πk3τ+W3 假设信道平坦,我们可以得到Hk1=Hk3,此处W3指代所有的噪声项 =∣Xk1,3∣2∣Xk3,3∣2∣Hk1∣2ejN2π(k3−k1)τ+W3
对99*2组导频进行累加,因为噪声W是白噪声,累加之后趋于0,可以忽略。
累加之后再开平方可得
N
p
2
∣
X
k
1
,
3
∣
∣
X
k
3
,
3
∣
∣
H
k
1
∣
e
j
2
π
(
k
3
−
k
1
)
2
N
τ
=
N
p
2
∣
X
k
1
,
3
∣
∣
X
k
3
,
3
∣
∣
H
k
1
∣
e
j
2
π
(
k
2
−
k
1
)
N
τ
\frac{N_p}{2}|X_{k_1,3}||X_{k_3,3}||H_{k_1}|e^{j \frac{2\pi (k_3 - k_1)}{2N} \tau}=\frac{N_p}{2}|X_{k_1,3}||X_{k_3,3}||H_{k_1}|e^{j \frac{2\pi (k_2 - k_1)}{N} \tau}
2Np∣Xk1,3∣∣Xk3,3∣∣Hk1∣ej2N2π(k3−k1)τ=2Np∣Xk1,3∣∣Xk3,3∣∣Hk1∣ejN2π(k2−k1)τ
对于该结果,我们求其角度值可得
θ
=
2
π
(
k
2
−
k
1
)
N
τ
\theta = \frac{2\pi (k_2 - k_1)}{N}\tau
θ=N2π(k2−k1)τ
根据帧结构我们可知
k
2
−
k
1
=
2
k_2 - k_1=2
k2−k1=2,
N
=
1024
N=1024
N=1024,带入即可求得时延
τ
=
θ
N
2
π
(
k
2
−
k
1
)
\tau=\frac{\theta N}{2 \pi (k_2 - k_1)}
τ=2π(k2−k1)θN
注意,由于
θ
\theta
θ的范围在
−
π
,
π
-\pi,\pi
−π,π之间,因此,可以估算出的时延
τ
\tau
τ是有一个范围的。
频偏估计(频率跟踪)
在已经求得时延
τ
\tau
τ的基础上,我们进一步求频偏
f
d
f_d
fd
接下来我们令:
(
Y
k
2
,
13
X
k
2
,
13
∗
)
(
Y
k
1
,
3
X
k
1
,
3
∗
)
∗
=
(
∣
X
k
2
,
13
∣
2
H
k
2
e
−
j
2
π
k
2
N
τ
e
j
2
π
f
d
△
t
+
W
k
2
,
13
)
(
∣
X
k
1
,
3
∣
2
H
k
1
e
−
j
2
π
k
1
N
τ
+
W
k
1
,
3
)
∗
=
∣
X
k
2
,
13
∣
2
∣
X
k
1
,
3
∣
2
H
k
2
H
k
1
∗
e
−
j
2
π
k
2
N
τ
e
j
2
π
k
1
N
τ
e
j
2
π
f
d
△
t
+
W
假设信道平坦,我们可以得到
H
k
1
=
H
k
2
,此处
W
指代所有的噪声项
=
∣
X
k
2
,
13
∣
2
∣
X
k
1
,
3
∣
2
∣
H
k
2
∣
2
e
j
2
π
(
k
1
−
k
2
)
N
τ
e
j
2
π
f
d
△
t
+
W
\begin{aligned} (Y_{k_2,13}X_{k_2,13}^*)(Y_{k_1,3}X_{k_1,3}^*)^* &= (|X_{k_2,13}|^2 H_{k_2} e^{-j \frac{2\pi k_2}{N} \tau}e^{j 2\pi f_d \bigtriangleup t}+W_{k_2,13})(|X_{k_1,3}|^2 H_{k_1} e^{-j \frac{2\pi k_1}{N} \tau}+W_{k_1,3})^* \\&=|X_{k_2,13}|^2|X_{k_1,3}|^2H_{k_2}H_{k_1}^*e^{-j \frac{2\pi k_2}{N} \tau}e^{j \frac{2\pi k_1}{N} \tau} e^{j 2\pi f_d \bigtriangleup t} +W \\&假设信道平坦,我们可以得到H_{k_1}=H_{k_2},此处W指代所有的噪声项 \\&=|X_{k_2,13}|^2|X_{k_1,3}|^2|H_{k_2}|^2e^{j \frac{2\pi (k_1-k_2) }{N} \tau} e^{j 2\pi f_d \bigtriangleup t} +W \end{aligned}
(Yk2,13Xk2,13∗)(Yk1,3Xk1,3∗)∗=(∣Xk2,13∣2Hk2e−jN2πk2τej2πfd△t+Wk2,13)(∣Xk1,3∣2Hk1e−jN2πk1τ+Wk1,3)∗ =∣Xk2,13∣2∣Xk1,3∣2Hk2Hk1∗e−jN2πk2τejN2πk1τej2πfd△t+W 假设信道平坦,我们可以得到Hk1=Hk2,此处W指代所有的噪声项 =∣Xk2,13∣2∣Xk1,3∣2∣Hk2∣2ejN2π(k1−k2)τej2πfd△t+W
累加可得
N
p
2
∣
X
k
2
,
13
∣
2
∣
X
k
1
,
3
∣
2
∣
H
k
2
∣
2
e
j
2
π
(
k
1
−
k
2
)
N
τ
e
j
2
π
f
d
△
t
\frac{N_p}{2}|X_{k_2,13}|^2|X_{k_1,3}|^2|H_{k_2}|^2e^{j \frac{2\pi (k_1-k_2) }{N} \tau} e^{j 2\pi f_d \bigtriangleup t}
2Np∣Xk2,13∣2∣Xk1,3∣2∣Hk2∣2ejN2π(k1−k2)τej2πfd△t
我们在求时延
τ
\tau
τ的时候就已经计算得到
N
p
2
∣
X
k
1
,
3
∣
∣
X
k
3
,
3
∣
∣
H
k
1
∣
e
j
2
π
(
k
2
−
k
1
)
N
τ
\frac{N_p}{2}|X_{k_1,3}||X_{k_3,3}||H_{k_1}|e^{j \frac{2\pi (k_2 - k_1)}{N} \tau}
2Np∣Xk1,3∣∣Xk3,3∣∣Hk1∣ejN2π(k2−k1)τ,二者相乘可得
N
p
2
4
∣
X
k
2
,
13
∣
2
∣
X
k
1
,
3
∣
2
∣
H
k
2
∣
2
∣
X
k
1
,
3
∣
∣
X
k
3
,
3
∣
∣
H
k
1
∣
e
j
2
π
(
k
1
−
k
2
+
k
2
−
k
1
)
N
τ
e
j
2
π
f
d
△
t
=
M
e
j
2
π
f
d
△
t
\frac{N_p^2}{4}|X_{k_2,13}|^2|X_{k_1,3}|^2|H_{k_2}|^2|X_{k_1,3}||X_{k_3,3}||H_{k_1}|e^{j \frac{2\pi (k_1-k_2+k_2-k_1) }{N} \tau} e^{j 2\pi f_d \bigtriangleup t} = M e^{j 2\pi f_d \bigtriangleup t}
4Np2∣Xk2,13∣2∣Xk1,3∣2∣Hk2∣2∣Xk1,3∣∣Xk3,3∣∣Hk1∣ejN2π(k1−k2+k2−k1)τej2πfd△t=Mej2πfd△t
对该结果求角度可得
θ
‘
=
2
π
f
d
△
t
{\theta}^` = 2\pi f_d \bigtriangleup t
θ‘=2πfd△t
△
t
\bigtriangleup t
△t为ofdm3和ofdm13的时间间隔,带入即可轻松求得频偏
f
d
=
θ
‘
2
π
△
t
f_d = \frac{{\theta}^` }{2\pi \bigtriangleup t}
fd=2π△tθ‘
注意,由于
θ
‘
{\theta}^`
θ‘的范围在
−
π
,
π
-\pi,\pi
−π,π之间,因此,可以估算出的频偏
f
d
f_d
fd是有一个范围的。