食用指南：本文在有C基础的情况下食用更佳 

                                       🔥这就不得不推荐此专栏了：C语言

                                       ♈️今日夜电波：透明で透き通って何にでもなれそうで—HaKU

                                                                2:05 ━━━━━━️💟──────── 5:38
                                                                    🔄   ◀️   ⏸   ▶️    ☰ 

                                      💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍 

---

目录

♉️一、前置知识—什么是插入排序

♊️二、直接插入排序

        直接插入排序的思想

        直接插入排序的实现 

        直接插入排序的效率 

♋️ 三、希尔排序

        希尔排序的思想

        希尔排序的实现 

       ♌️ 希尔排序的效率 

---

♉️一、前置知识—什么是插入排序

        插入排序的基本思想是将一个待排序的序列逐个插入到已经排好序的序列中，直到全部元素都插入完成。每次插入一个元素时，将它与已经排好序的元素逐个比较，找到它在已排好序列中的位置，并插入到该位置。具体实现时，可以将待排序序列分为已排序和未排序两部分，从未排序序列中依次取出元素逐个插入已排序序列中，直到待排序序列为空为止。

         一个形象的🌰：

        日常生活中我们在玩扑克时：将每一张牌都插入到一个有序的位置就是一种插入排序：

---

♊️二、直接插入排序

        直接插入排序的思想

        其基本思想是将待排序的元素插入到已经有序的序列中，使得插入后的序列仍然有序。

        具体操作步骤如下：

1. 将第一个元素看作已经排好序的序列。
2. 依次将后面的元素插入到前面已经排好序的序列中。
3. 对于未排序的元素，从后往前依次比较，若比前一个元素小则交换位置，直到找到合适的位置插入。
4. 重复步骤2和3，直到所有元素都插入到已排序的序列中。

        一张经典的插入排序动图让你理解： 

 

        直接插入排序的实现 

        详细见代码内的注释。

void InsertSort(int* a, int n)
{
	// [0,end]有序，把end+1位置的插入到前序序列
	// 控制[0,end+1]有序
	for (int i = 0; i < n - 1; i++)//遍历每一个元素
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (tmp < a[end])//当后一个元素也就是tmp小于前面的某一个元素时先将前一个元素后移
			{
				a[end + 1] = a[end];
			}
			else//只要找到大于tmp的元素，直接跳出，然后插在这个元素后
			{
				break;
			}

			--end;//向前移动操作
		}

		a[end + 1] = tmp;//将要插入的元素也就是最后的元素插入到相应的位置
	}
}

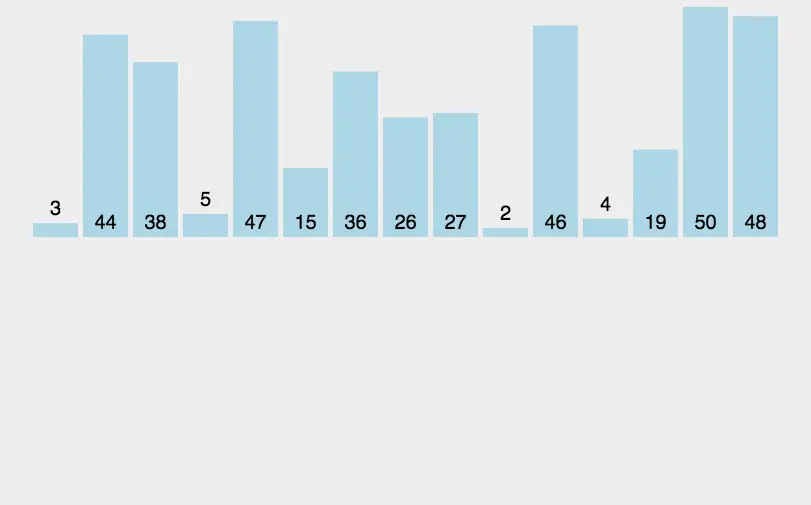
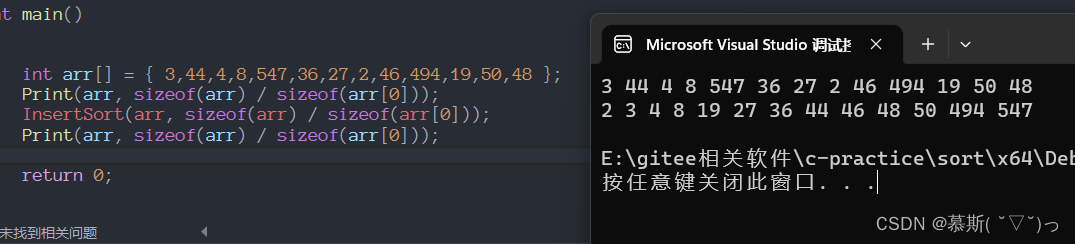
        实现效果：

void Print(int* arr,int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}

	printf("\n");
}

int main()
{
	
	int arr[] = { 3,44,4,8,547,36,27,2,46,494,19,50,48 };
	Print(arr, sizeof(arr) / sizeof(arr[0]));
	InsertSort(arr, sizeof(arr) / sizeof(arr[0]));
	Print(arr, sizeof(arr) / sizeof(arr[0]));

	return 0;
}

 

        直接插入排序的效率 

        1. 元素集合越接近有序，直接插入排序算法的时间效率越高
        2. 时间复杂度：O(N^2)
        3. 空间复杂度：O(1)，它是一种稳定的排序算法
        4. 稳定性：稳定

 

---

♋️ 三、希尔排序

        希尔排序的思想

        希尔排序通过将待排序的数组按照一定的间隔分组，对每组使用插入排序算法进行排序，随着间隔的逐渐缩小，每组包含的元素数量逐渐增多，当间隔缩小至1时，整个序列被分成一组，算法便终止。

        

        希尔排序的步骤如下：

1. 首先选定一个增量gap，一般设置为数组长度的1/2，之后以gap为步长，将整个数组分为多个子序列（每个子序列长度为gap）。
2. 对于每个子序列，使用插入排序算法进行排序。
3. 缩小gap，重复第2步操作，直至gap为1时，整个序列被分成一组，算法终止。

         两张经典的图让你理解：

  

 

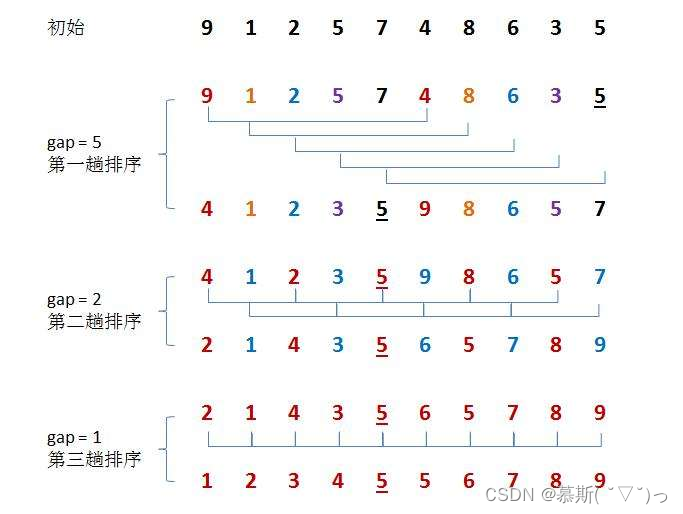
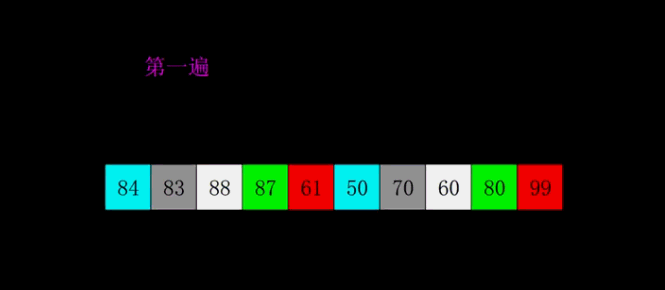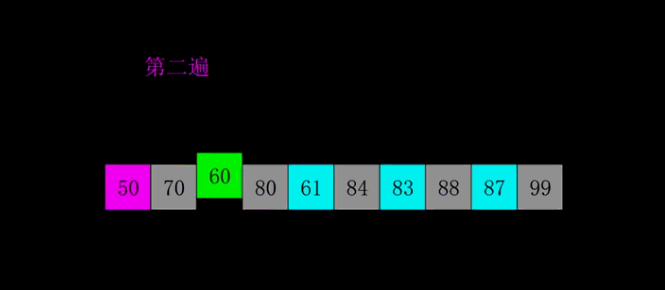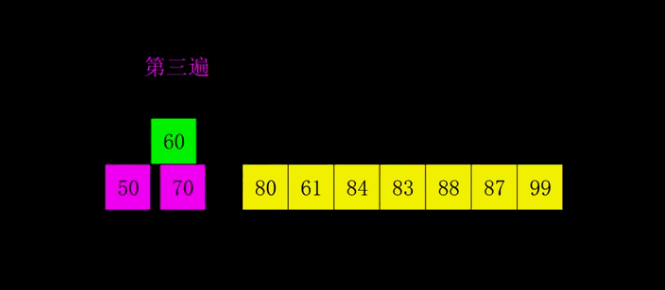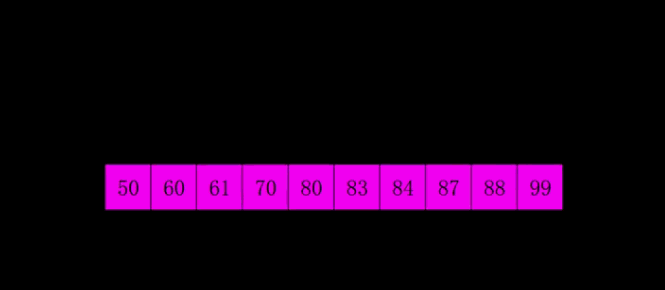
        希尔排序的实现 

         详细见代码内的注释。

void ShellSort(int* a, int n)
{
	int gap = n;//首先，计算出最初的步长（通常为数组长度的一半）
	while (gap > 1)
	{
		gap = gap / 2;//对每个步长进行循环，直至步长为1
		//gap = gap / 3 + 1;//还有一种说法是每次除以3的步长，+1是为了保证最后gap==1

		for (int i = 0; i < n - gap; ++i)//前几次为预排序，其实就是步长为gap的插入排序，当gap==1时就是插入排序了
		{
			int end = i;
			int tmp = a[end + gap];//按步长找到后一个元素
			while (end >= 0)
			{
				if (tmp < a[end])//当后一个元素也就是tmp小于前面的某一个元素时先将前一个元素后移
				{
					a[end + gap] = a[end];
				}
				else//只要找到大于tmp的元素，直接跳出，然后插在这个元素后
				{
					break;
				}
				end -= gap;//向前移动操作
			}
			a[end + gap] = tmp;//将要插入的元素也就是最后的元素插入到相应的位置
		}
	}
}

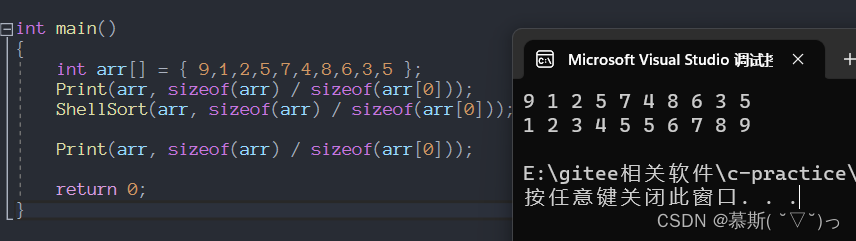
            实现效果： 

void Print(int* arr,int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}

	printf("\n");
}

int main()
{
	int arr[] = { 9,1,2,5,7,4,8,6,3,5 };
	Print(arr, sizeof(arr) / sizeof(arr[0]));
	ShellSort(arr, sizeof(arr) / sizeof(arr[0]));

	Print(arr, sizeof(arr) / sizeof(arr[0]));

	return 0;
}

        

       ♌️ 希尔排序的效率 

        希尔排序的效率取决于增量序列的选择。较好的增量序列可以使希尔排序比插入排序和选择排序等简单排序算法更加高效，但是对于不同的数据集，效率可能会有所差异。平均时间复杂度为O(n^1.3)，最坏时间复杂度为O(n^2)。希尔排序虽然不如快速排序和归并排序等高级排序算法，但是在某些特定场景下具有很好的性能表现。

 

---

                    感谢你耐心的看到这里ღ( ´･ᴗ･` )比心，如有哪里有错误请踢一脚作者o(╥﹏╥)o！ 

                                       

                                                                         给个三连再走嘛~