【1971. 寻找图中是否存在路径】

来源：力扣（LeetCode）

描述：

有一个具有 n 个顶点的双向图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。每个顶点对由最多一条边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的有效路径。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在有效路径，则返回 true，否则返回 false 。

示例 1：

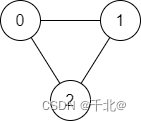
输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2 
- 0 → 2

示例 2：

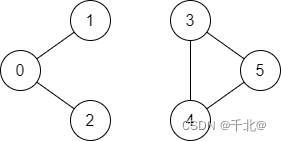
输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

提示：

1 <= n <= 2 * 10⁵
0 <= edges.length <= 2 * 10⁵
edges[i].length == 2
0 <= ui, vi <= n - 1
ui != vi
0 <= source, destination <= n - 1
不存在重复边
不存在指向顶点自身的边

前言

题目要求判断是否存在从起点 source 到终点 destination 的有效路径，等价于求图中两个顶点 source, destination 是否连通。两点连通性问题为经典问题，一般我们可以使用广度优先搜索或深度优先搜索，以及并查集来解决。

方法一：广度优先搜索

思路与算法

使用广度优先搜索判断顶点 source 到顶点 destination 的连通性，需要我们从顶点 source 开始按照层次依次遍历每一层的顶点，检测是否可以到达顶点 destination。遍历过程我们使用队列存储最近访问过的顶点，同时记录每个顶点的访问状态，每次从队列中取出顶点 vertex 时，将其未访问过的邻接顶点入队列。

初始时将顶点 source 设为已访问，并将其入队列。每次将队列中的节点 vertex 出队列，并将与 vertex 相邻且未访问的顶点 next 入队列，并将 next 设为已访问。当队列为空或访问到顶点 destination 时遍历结束，返回顶点 destination 的访问状态即可。

代码：

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<vector<int>> adj(n);
        for (auto &&edge : edges) {
            int x = edge[0], y = edge[1];
            adj[x].emplace_back(y);
            adj[y].emplace_back(x);
        }
        vector<bool> visited(n, false);
        queue<int> qu;
        qu.emplace(source);
        visited[source] = true;
        while (!qu.empty()) {
            int vertex = qu.front();
            qu.pop();
            if (vertex == destination) {
                break;
            }
            for (int next: adj[vertex]) {
                if (!visited[next]) {
                    qu.emplace(next);
                    visited[next] = true;
                }
            }
        }
        return visited[destination];
    }
};

执行用时：632 ms, 在所有 C++ 提交中击败了15.39%的用户
内存消耗：145.6 MB, 在所有 C++ 提交中击败了38.17%的用户
复杂度分析
时间复杂度：O(n + m)，其中 n 表示图中顶点的数目，m 表示图中边的数目。对于图中的每个顶点或者每条边，我们最多只需访问一次，因此时间复杂度为 O(n + m)。
空间复杂度：O(n + m)，其中nn 表示图中顶点的数目，m 表示图中边的数目。空间复杂度主要取决于邻接顶点列表、记录每个顶点访问状态的数组和队列，邻接顶点列表需要的空间为 O(n + m)，记录访问状态需要 O(n) 的空间，进行广度优先搜索时队列中最多只有 n 个元素，因此总的空间复杂度为 (n + m)。

方法二：深度优先搜索

思路与算法

我们使用深度优先搜索检测顶点 source, destination 的连通性，需要从顶点 source 开始依次遍历每一条可能的路径，判断可以到达顶点 destination，同时还需要记录每个顶点的访问状态防止重复访问。

首先从顶点 source 开始遍历并进行递归搜索。搜索时每次访问一个顶点 \textit{vertex} vertex 时，如果 vertex 等于 destination 则直接返回，否则将该顶点设为已访问，并递归访问与 vertex 相邻且未访问的顶点 next。如果通过 next 的路径可以访问到 destination，此时直接返回 true，当访问完所有的邻接节点仍然没有访问到 destination，此时返回 false。

代码:

class Solution {
public:
    bool dfs(int source, int destination, vector<vector<int>> &adj, vector<bool> &visited) {
        if (source == destination) {
            return true;
        }
        visited[source] = true;
        for (int next : adj[source]) {
            if (!visited[next] && dfs(next, destination, adj, visited)) {
                return true;
            }
        }
        return false;
    }

    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<vector<int>> adj(n);
        for (auto &edge : edges) {
            int x = edge[0], y = edge[1];
            adj[x].emplace_back(y);
            adj[y].emplace_back(x);
        }
        vector<bool> visited(n, false);
        return dfs(source, destination, adj, visited);
    }
};

执行用时：496 ms, 在所有 C++ 提交中击败了33.71%的用户
内存消耗：207.4 MB, 在所有 C++ 提交中击败了11.33%的用户
复杂度分析
时间复杂度：O(n + m)，其中 n 表示图中顶点的数目，m 表示图中边的数目。对于图中的每个顶点或者每条边，我们最多只需访问一次，对于每个顶因此时间复杂度为 O(n + m)。
空间复杂度：O(n + m)，其中 n 表示图中顶点的数目，m 表示图中边的数目。空间复杂度主要取决于邻接顶点列表、记录每个顶点访问状态的数组和递归调用栈，邻接顶点列表需要 O(m + n)的存储空间，记录每个顶点访问状态的数组和递归调用栈分别需要 O(n)O(n) 的空间，因此总的空间复杂度为 O(m + n)。

方法三：并查集

思路与算法

我们将图中的每个强连通分量视为一个集合，强连通分量中任意两点均可达，如果两个点 source 和 destination 处在同一个强连通分量中，则两点一定可连通，因此连通性问题可以使用并查集解决。

并查集初始化时，n 个顶点分别属于 n 个不同的集合，每个集合只包含一个顶点。初始化之后遍历每条边，由于图中的每条边均为双向边，因此将同一条边连接的两个顶点所在的集合做合并。

遍历所有的边之后，判断顶点 source 和顶点 destination 是否在同一个集合中，如果两个顶点在同一个集合则两个顶点连通，如果两个顶点所在的集合不同则两个顶点不连通。

代码:

class UnionFind {
public:
    UnionFind(int n) {
        parent = vector<int>(n);
        rank = vector<int>(n);
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    void uni(int x, int y) {
        int rootx = find(x);
        int rooty = find(y);
        if (rootx != rooty) {
            if (rank[rootx] > rank[rooty]) {
                parent[rooty] = rootx;
            } else if (rank[rootx] < rank[rooty]) {
                parent[rootx] = rooty;
            } else {
                parent[rooty] = rootx;
                rank[rootx]++;
            }
        }
    }

    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    bool connect(int x, int y) {
        return find(x) == find(y);
    }
private:
    vector<int> parent;
    vector<int> rank;
};

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        if (source == destination) {
            return true;
        }
        UnionFind uf(n);
        for (auto edge : edges) {
            uf.uni(edge[0], edge[1]);
        }
        return uf.connect(source, destination);
    }
};

执行用时：360 ms, 在所有 C++ 提交中击败了55.85%的用户
内存消耗：124.8 MB, 在所有 C++ 提交中击败了43.39%的用户
复杂度分析
时间复杂度： O(n + m × α(m))，其中 n 是图中的顶点数，m 是图中边的数目，α 是反阿克曼函数。并查集的初始化需要 O(n) 的时间，然后遍历 m 条边并执行 m 次合并操作，最后对 source 和 destination 执行一次查询操作，查询与合并的单次操作时间复杂度是 O(α(m))，因此合并与查询的时间复杂度是 O(m×α(m))，总时间复杂度是O(n+m×α(m))。
空间复杂度：O(n)，其中 n 是图中的顶点数。并查集需要 O(n) 的空间。
author：LeetCode-Solution