#【中秋征文】程序人生,中秋共享#
目录
第一题
题目来源
题目内容
解决方法
方法一:遍历字符串
方法二:有限状态机(Finite State Machine)
方法三:正则表达式
第二题
题目来源
题目内容
解决方法
方法一:反转数字比较
第三题
题目来源
题目内容
解决方法
方法一:动态规划
方法二:递归回溯
第一题
题目来源
8. 字符串转换整数 (atoi) - 力扣(LeetCode)
题目内容

解决方法
方法一:遍历字符串
题目要求实现一个字符串转换整数的函数,即将给定字符串转换成一个32位有符号整数。
解题思路如下:
-
去除字符串开头的空格。
-
判断接下来的字符是否为正号或者负号,如果是则记录符号并向后移动一位。
-
遍历剩余的字符串字符,直到遇到非数字字符为止。将遇到的数字字符转换成整数,并累加到结果中。
-
根据符号和结果判断最终返回的整数值。
-
注意处理越界情况,如果超出32位有符号整数的取值范围,则返回边界值。
class Solution {
public int myAtoi(String s) {
// 去除前导空格
s = s.trim();
// 处理空字符串和只有正负号的情况
if (s.length() == 0 || (s.length() == 1 && (s.charAt(0) == '+' || s.charAt(0) == '-'))) {
return 0;
}
// 判断第一个非空字符是否为正负号
boolean positive = true;
int i = 0;
if (s.charAt(0) == '+' || s.charAt(0) == '-') {
if (s.charAt(0) == '-') {
positive = false;
}
i++;
}
// 提取连续的数字字符并转换为整数
long result = 0; // 使用长整型,防止溢出
while (i < s.length() && Character.isDigit(s.charAt(i))) {
int digit = s.charAt(i) - '0';
result = result * 10 + digit;
// 判断是否超出范围
if (positive && result > Integer.MAX_VALUE) {
return Integer.MAX_VALUE;
} else if (!positive && result * -1 < Integer.MIN_VALUE) {
return Integer.MIN_VALUE;
}
i++;
}
// 根据正负号返回最终结果
return positive ? (int)result : (int)(result * -1);
}
}这个函数首先去除字符串的前导空格,然后判断字符串是否为空或只有正负号的情况,如果是,则返回0。接下来,判断第一个非空字符是正号还是负号,并将其处理为正负标志。然后,遍历字符串的剩余部分,将连续的数字字符转换为整数,并判断是否超出范围。最后,根据正负标志返回最终结果。
下面是该解决方案的复杂度分析:
- 时间复杂度:O(n),其中 n 是字符串的长度。在算法中,我们只遍历字符串一次。
- 空间复杂度:O(1)。除了存储结果之外,算法使用的额外空间是固定大小的变量,并不随输入的规模而改变。
需要注意的是,在判断是否超出范围时,我们使用了长整型变量 result,而不是直接使用整型变量。这是因为如果 result 溢出 32 位有符号整数的范围,将无法正确判断溢出。所以我们将连续数字字符转换为长整型,然后再判断是否超出范围,并根据正负号返回最终结果。
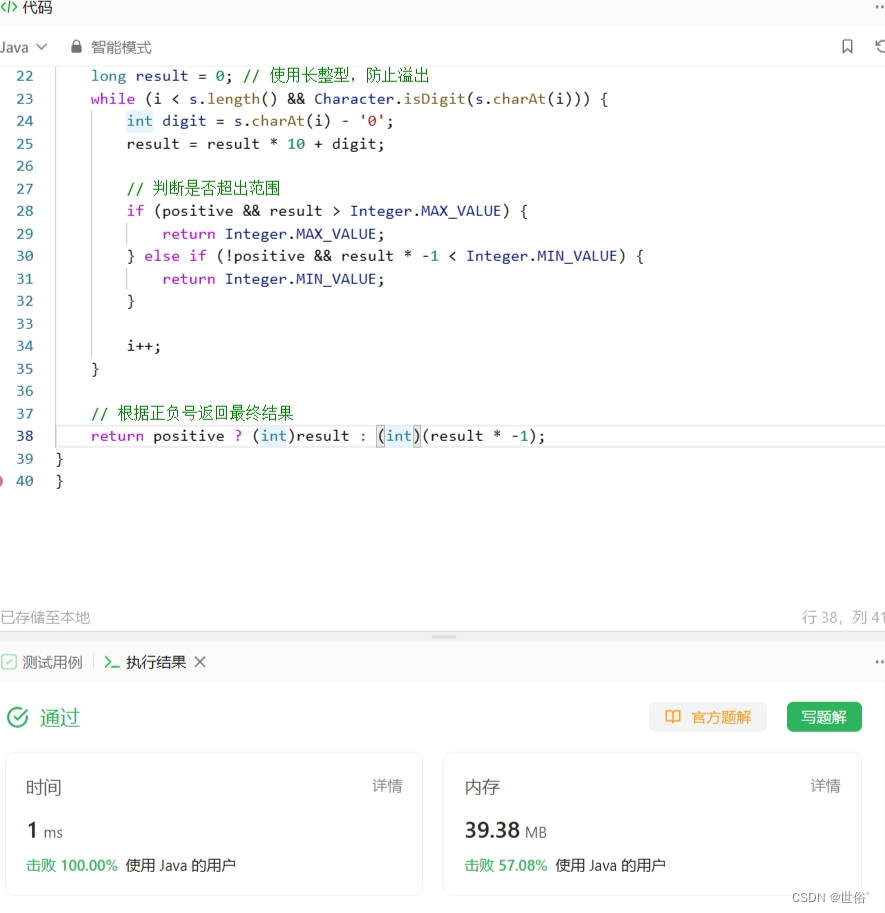
LeetCode运行结果:
方法二:有限状态机(Finite State Machine)
还有其他方法可以解决这个问题。一种常见的方法是使用有限状态机(Finite State Machine)。有限状态机的基本思想是根据输入的字符和当前状态进行状态转移,最终得到结果。
class Solution {
public int myAtoi(String s) {
Automaton automaton = new Automaton();
for (char c : s.toCharArray()) {
if (!automaton.process(c)) {
break;
}
}
return (int) (automaton.sign * automaton.result);
}
class Automaton {
public int sign = 1; // 符号,默认为正号
public long result = 0; // 结果,默认为0
private String state = "start"; // 初始状态
private Map<String, String[]> transitionTable = new HashMap<>(){{
put("start", new String[]{"start", "signed", "inNumber", "end"});
put("signed", new String[]{"end", "end", "inNumber", "end"});
put("inNumber", new String[]{"end", "end", "inNumber", "end"});
put("end", new String[]{"end", "end", "end", "end"});
}};
public boolean process(char c) {
state = transitionTable.get(state)[getStateIndex(c)];
if ("inNumber".equals(state)) {
result = result * 10 + (c - '0');
result = sign == 1 ? Math.min(result, Integer.MAX_VALUE) : Math.min(result, -1L * Integer.MIN_VALUE);
} else if ("signed".equals(state)) {
sign = c == '+' ? 1 : -1;
} else if ("end".equals(state)) {
return false;
}
return true;
}
private int getStateIndex(char c) {
if (c == ' ') {
return 0;
}
if (c == '+' || c == '-') {
return 1;
}
if (Character.isDigit(c)) {
return 2;
}
return 3;
}
}
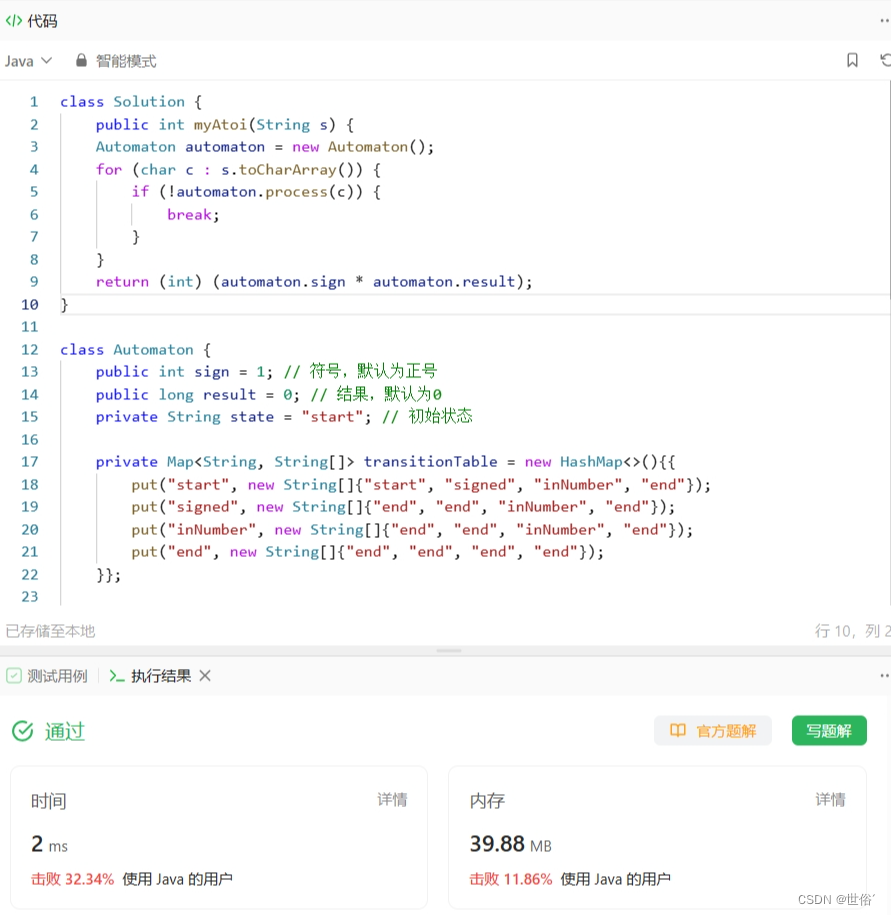
}在这个解决方案中,我们使用了一个包含四个状态的有限状态机。根据当前状态和输入字符的类型,我们进行状态转移,并更新符号和结果。具体的状态转移规则可以在 transitionTable 中定义。
这个解决方案的时间复杂度为 O(n),空间复杂度为 O(1)。
LeetCode运行结果:
方法三:正则表达式
正则表达式是一种强大的模式匹配工具,可以用来匹配和提取字符串中的特定模式。
import java.util.regex.Pattern;
import java.util.regex.Matcher;
class Solution {
public int myAtoi(String s) {
String pattern = "^\\s*([+-]?\\d+)";
Pattern regex = Pattern.compile(pattern);
Matcher matcher = regex.matcher(s);
if(matcher.find()) {
try {
long num = Long.parseLong(matcher.group(1));
if (num > Integer.MAX_VALUE) {
return Integer.MAX_VALUE;
} else if (num < Integer.MIN_VALUE) {
return Integer.MIN_VALUE;
} else {
return (int) num;
}
} catch (NumberFormatException e) {
// 处理超出整数范围的情况
if (matcher.group(1).charAt(0) == '-') {
return Integer.MIN_VALUE;
} else {
return Integer.MAX_VALUE;
}
}
}
return 0; // 如果无法匹配数字,则返回0
}
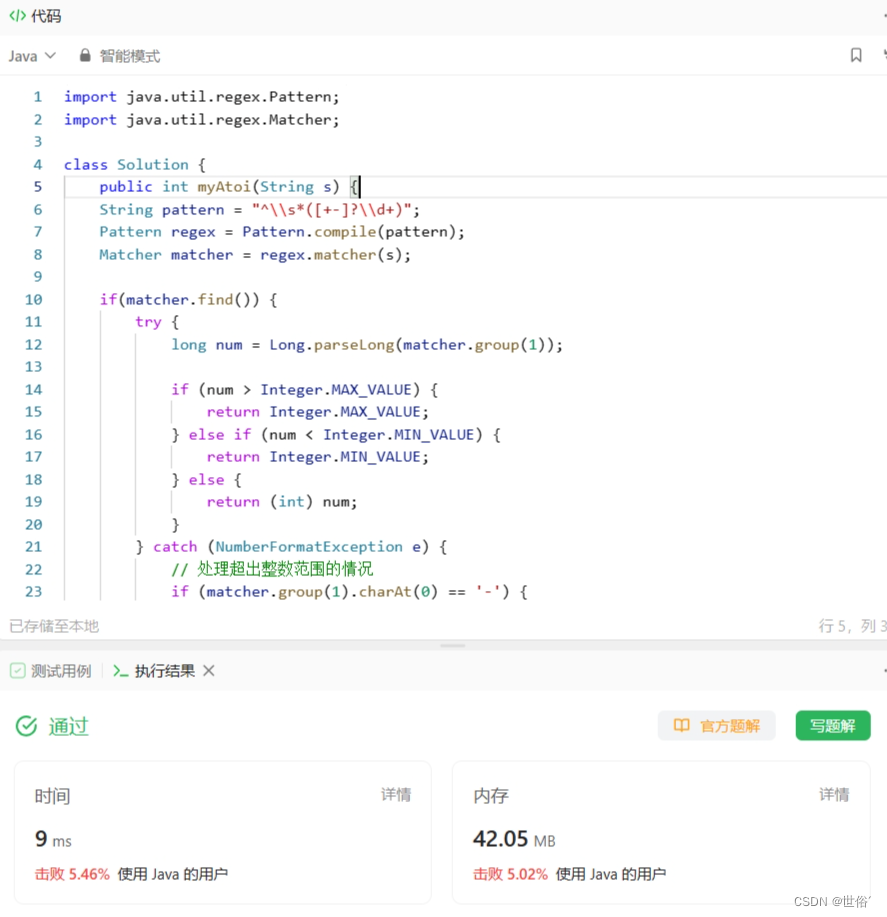
}在这个解决方案中,我们使用了正则表达式 ^\\s*([+-]?\\d+) 来匹配字符串中的数字。首先,使用 Pattern 类编译正则表达式,并使用 Matcher 类对输入字符串进行匹配。如果在字符串中找到一个或多个数字序列,我们尝试将其转换为长整型 num。然后,我们检查 num 是否超出了整数的范围,并根据结果返回相应的值。
这个解决方案的时间复杂度取决于正则表达式的匹配速度,通常为 O(n)。空间复杂度为 O(1),因为只使用了有限的变量来存储结果。
LeetCode运行结果:
第二题
题目来源
9. 回文数 - 力扣(LeetCode)
题目内容

解决方法
方法一:反转数字比较
class Solution {
public boolean isPalindrome(int x) {
// 处理特殊情况,负数和以0结尾的非零数不可能是回文数
if (x < 0 || (x % 10 == 0 && x != 0)) {
return false;
}
int reverse = 0;
int original = x;
while (x > 0) {
int digit = x % 10;
reverse = reverse * 10 + digit;
x /= 10;
}
return original == reverse;
}
}在这个解决方案中,我们首先处理了一些特殊情况:负数和以0结尾的非零数不可能是回文数。然后,我们使用一个循环,将输入的数字逐位反转并保存到变量 reverse 中。最后,我们检查反转后的数字是否等于原始数字 x。
这个方法的时间复杂度是 O(log n),其中 n 是 x 的位数。空间复杂度是 O(1)。
LeetCode运行结果:
第三题
题目来源
10. 正则表达式匹配 - 力扣(LeetCode)
题目内容

解决方法
方法一:动态规划
这是一个经典的正则表达式匹配问题,可以使用动态规划来解决。具体的思路如下:
- 定义一个二维布尔数组 dp,其中 dp[i][j] 表示 s 的前 i 个字符是否与 p 的前 j 个字符匹配。
- 初始化 dp[0][0] 为 true,表示空字符可以匹配。
- 对于第一行 dp[0][j]:如果 p[j-1] 是 '',则可以把 p[j-2] 和 '' 一起消去,即 dp[0][j] = dp[0][j-2];否则为 false。
- 对于其他行 dp[i][j]:
- 如果 p[j-1] 是字母或者 '.',则判断当前字符能否匹配,即 dp[i][j] = dp[i-1][j-1];
- 如果 p[j-1] 是 '*',有两种情况:
- "表示匹配零次前面的元素,即将 p[j-2] 和 "一起消去,即 dp[i][j] = dp[i][j-2];
- '*' 表示匹配一次或多次前面的元素,即当前字符与 p[j-2] 匹配且前一个字符匹配(dp[i-1][j])。
最后,返回 dp[s.length()][p.length()]。
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length();
int n = p.length();
// 创建并初始化 dp 数组
boolean[][] dp = new boolean[m + 1][n + 1];
dp[0][0] = true; // 空字符串和空模式匹配
// 处理边界情况,s 为空字符串时的匹配
for (int j = 1; j <= n; j++) {
if (p.charAt(j - 1) == '*') {
dp[0][j] = dp[0][j - 2]; // '*' 可以将前面的字符匹配 0 次
}
}
// 动态规划求解
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 如果当前字符匹配,则和上一个字符的匹配结果一致
if (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.') {
dp[i][j] = dp[i - 1][j - 1];
} else if (p.charAt(j - 1) == '*') {
// 如果遇到 '*' 字符,有两种情况:
// 1. '*' 匹配了前一个字符 0 次,则和 p 的前两个字符匹配结果一致
// 2. '*' 匹配了前一个字符多次,则当前字符和前面的模式字符串匹配,
// 并且和上一个字符的匹配结果一致
dp[i][j] = dp[i][j - 2]; // 匹配 0 次的情况
if (p.charAt(j - 2) == '.' || p.charAt(j - 2) == s.charAt(i - 1)) {
dp[i][j] = dp[i][j] || dp[i - 1][j];
}
}
}
}
return dp[m][n];
}
}这个算法的时间复杂度是 O(m * n),其中 m 是字符串 s 的长度,n 是模式 p 的长度。空间复杂度是 O(m * n)。
LeetCode运行结果:
方法二:递归回溯
除了动态规划,还可以使用递归回溯的方法来解决。具体的思路是从左到右依次匹配字符,对于每个字符,有如下几种情况:
- 如果当前字符和模式字符相同,或者模式字符是 '.',则继续匹配下一个字符。
- 如果模式字符是 '*',有两种情况:
- 模式字符和前一个字符不匹配,并且当前字符也和模式字符的前一个字符不匹配,则只能将 '*' 视为匹配 0 次前面的字符,继续匹配后面的字符。
- 其他情况下,可以将 '*' 视为匹配 0 次、1 次或多次前面的字符,然后继续匹配下一个字符。
如果能够成功匹配到最后一个字符,则字符串和字符规律匹配成功。
class Solution {
public boolean isMatch(String s, String p) {
if (p.isEmpty()) {
return s.isEmpty();
}
boolean firstMatch = !s.isEmpty() && (s.charAt(0) == p.charAt(0) || p.charAt(0) == '.');
if (p.length() >= 2 && p.charAt(1) == '*') {
return isMatch(s, p.substring(2)) || (firstMatch && isMatch(s.substring(1), p));
} else {
return firstMatch && isMatch(s.substring(1), p.substring(1));
}
}
}复杂度分析:
- 时间复杂度:最坏情况下,对于每个字符都存在两种选择(匹配 0 次或多次),因此时间复杂度是指数级的,即 O(2^(m + n)),其中 m 和 n 分别是字符串 s 和模式 p 的长度。
- 空间复杂度:递归过程中需要消耗额外的栈空间,最坏情况下递归深度是字符串 s 和模式 p 的长度的和,因此空间复杂度为 O(m + n)。
综上所述,动态规划方法在时间和空间复杂度上都优于递归回溯方法。在实际应用中,建议使用动态规划方法来解决这个问题,尤其是在输入规模较大时。
LeetCode运行结果: