"回忆里的我,比国王富有。奢侈的快乐~"
1、前缀和【模板】
(1) 题目解析

(2) 算法原理 
#include <iostream>
using namespace std;
const int N = 100010;
// 可能出现溢出
long long arr[N],dp[N];
int n,q;
int main() {
cin >> n >> q;
// 初始化数组
for(int i=1;i<=n;++i) cin >> arr[i];
// 创建dp
for(int i = 1; i <= n; i++) dp[i] = dp[i - 1] + arr[i];
// 查询
while(q--){
int l,r;
cin >> l >> r;
// 计算区间和
cout << dp[r] - dp[l - 1] << endl;
}
return 0;
}
2、DP35 【模板】二维前缀和
(1) 题目解析
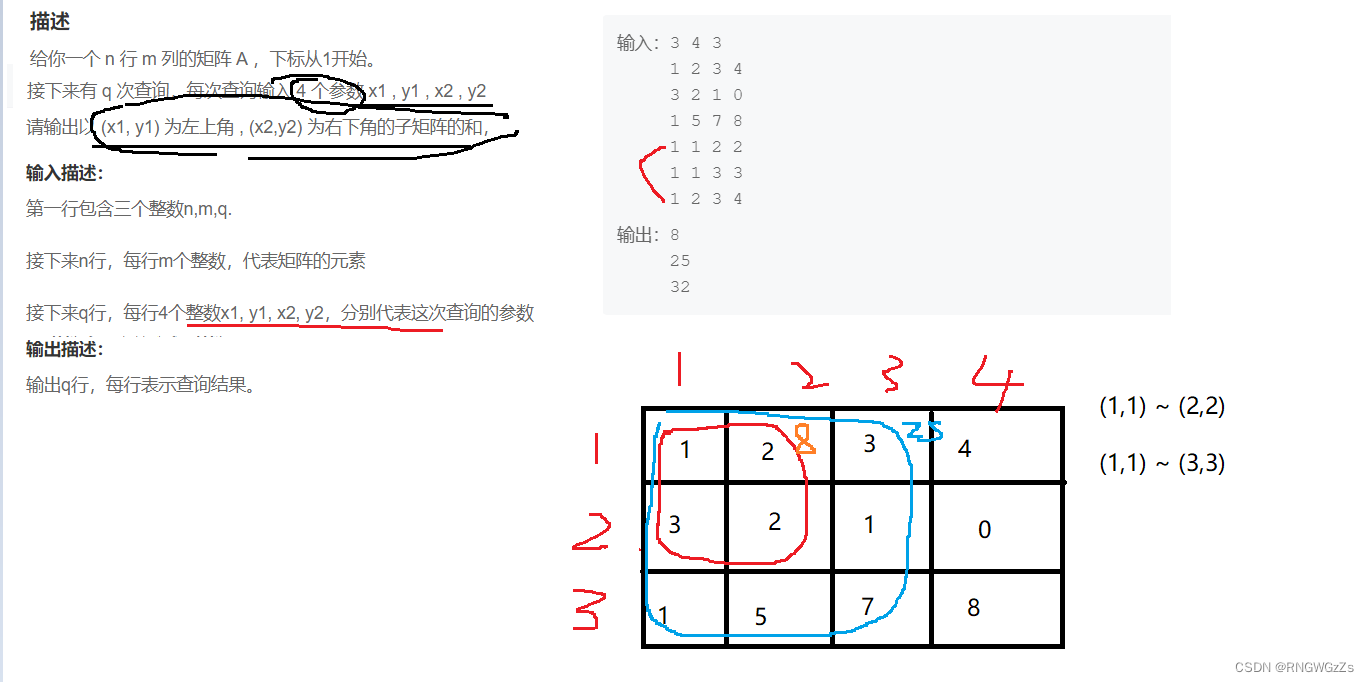
同一维前缀和类似,这类题型都需要预处理出前缀和数组,再求和。
(2) 算法原理
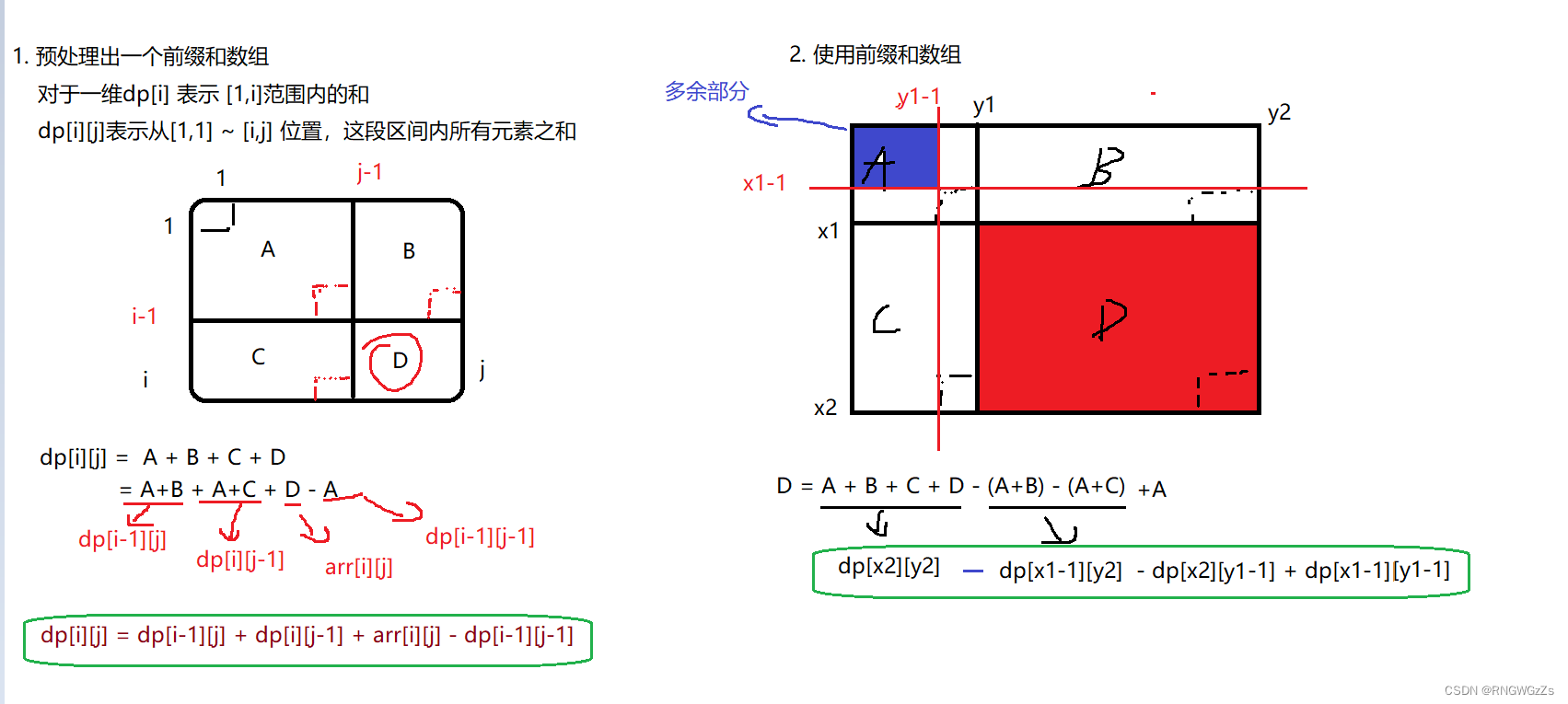
#include <iostream>
using namespace std;
const int N = 1010;
int main() {
int n, m, q;
long long arr[N][N], dp[N][N];
cin >> n >> m >> q;
// 输入数组
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
cin >> arr[i][j];
// 预处理前缀和
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];
// 查询
int x1,y1,x2,y2;
while(q--)
{
cin >> x1 >> y1 >> x2 >> y2;
cout << dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1] << endl;
}
return 0;
}3、寻找数组的中心下标
(1) 题目解析

本题的核心在于,存在一个mid,使得sum(0,mid-1) == sum(mid+1,end)。所以,我们只需要求得 (0,mid-1) 区间的值 是否等于 (mid+1,end)的值,就可以判断该mid 是否是中心下标。
(2) 算法原理 
class Solution {
public:
int pivotIndex(vector<int>& nums) {
int n = nums.size();
vector<int> f(n+1);
vector<int> g(n+1);
// 初始化前缀和
f[0] = g[n-1] = 0;
for(int i =1;i<=n;++i) f[i] = f[i-1] + nums[i-1];
for(int i =n-2;i>=0;--i) g[i] = g[i+1] + nums[i+1];
// 判断 0~n-1 迭代下标
for(int i=0;i<n;++i){
if(f[i] == g[i]) return i;
}
return -1;
}
};4、除自身以外数组的乘积
(1) 题目解析 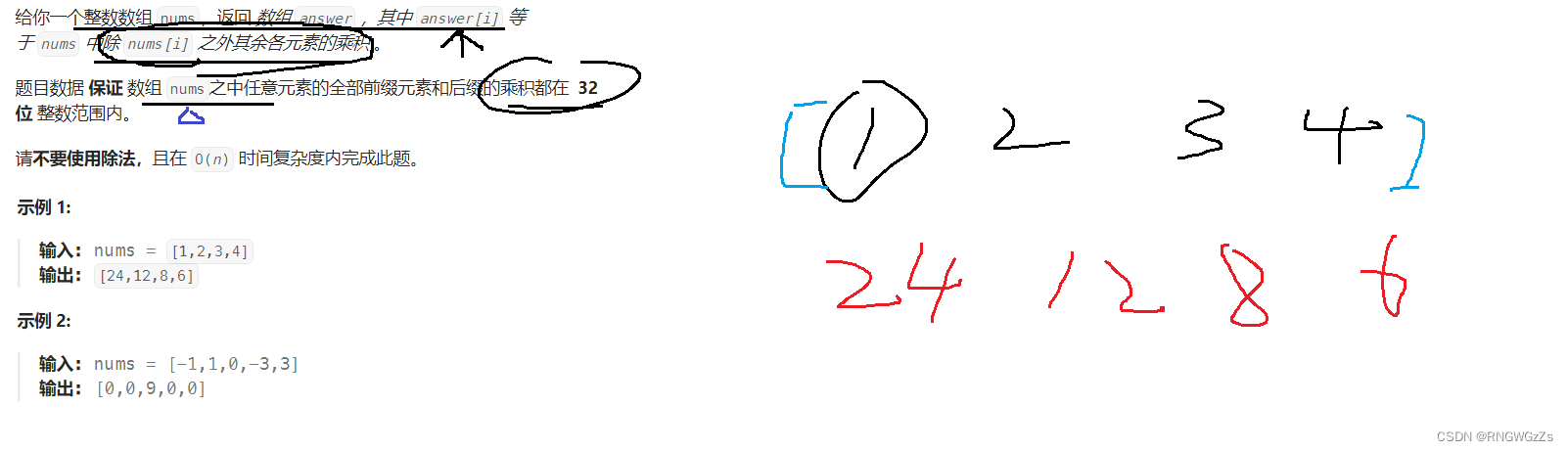
(2) 算法原理 
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> f(n+1);
vector<int> g(n+1);
// 初始化前缀和
f[0] = g[n-1] = 1;
for(int i=1;i<=n;++i) f[i] = f[i-1]*nums[i-1];
for(int i=n-2;i>=0;--i) g[i] = g[i+1]*nums[i+1];
// 判断
vector<int> ret;
for(int i=0;i<n;++i)
{
ret.push_back(f[i] * g[i]);
}
return ret;
}
};5、和为 K 的子数组
(1) 题目解析
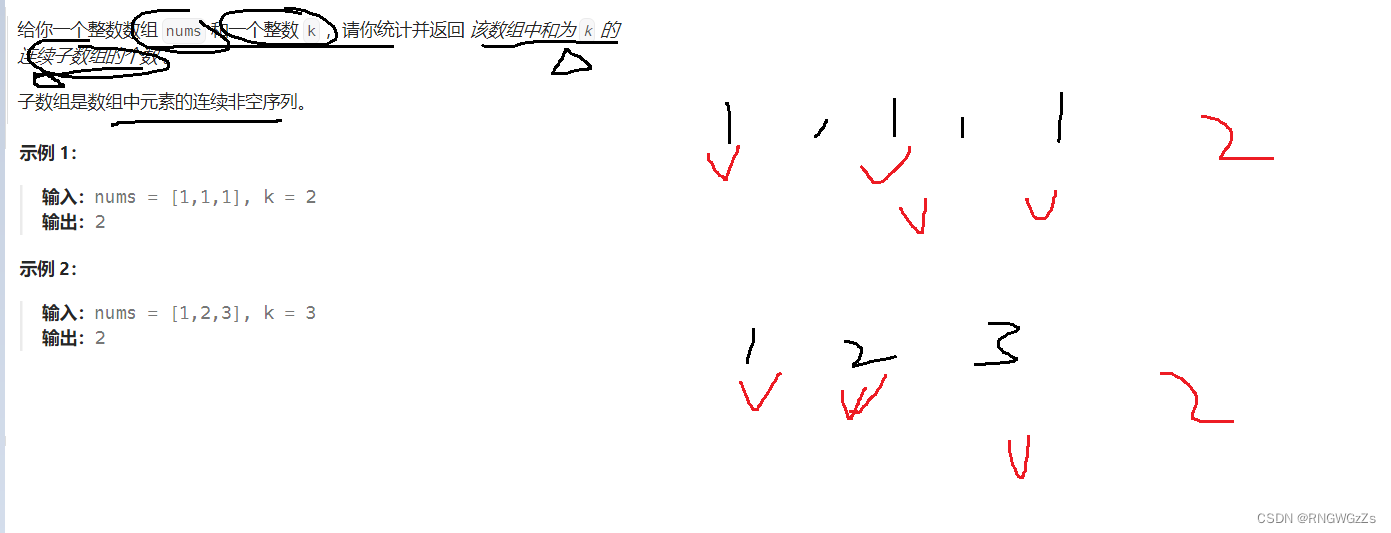
什么是子数组? 子数组一定是连续的 --> 这本质对应的是前缀和因为前缀和就是连续区间。
(2) 算法原理 
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int,int> hash;
hash[0] = 1; // 细节处理
int sum = 0; // 模拟前缀和
int count = 0;
for(auto& num:nums)
{
sum += num;
if(hash.count(sum-k)){
// 该元素存在
// 有多少个这个元素 就能找出多少个k
count += hash[sum-k];
}
// 该元素值个数++
hash[sum]++;
}
return count;
}
};6、和可被 K 整除的子数组
(1) 题目解析 
相比于上题,这道题无非条件做了些改变,在数组里找到能被k整除的前缀和。不过在开始这道题之前,我们得补充另外一个知识。
同余定理:
给定一个正整数m,如果两个整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余,记作a≡b(mod m)。对模m同余是整数的一个等价关系。
简单来说,就是这样:

有了上述的基础,我们再来认识认识这道题。
(2) 算法原理

class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k) {
unordered_map<int, int> hash;
hash[0 % k] = 1; // 0 这个数的余数
int sum = 0,ret = 0;
for(auto& n:nums)
{
sum += n;
int r = (sum % k + k) % k; // 修正后的余数
if(hash.count(r)) ret += hash[r];
hash[r]++;
}
return ret;
}
};7、连续数组
(1) 题目解析
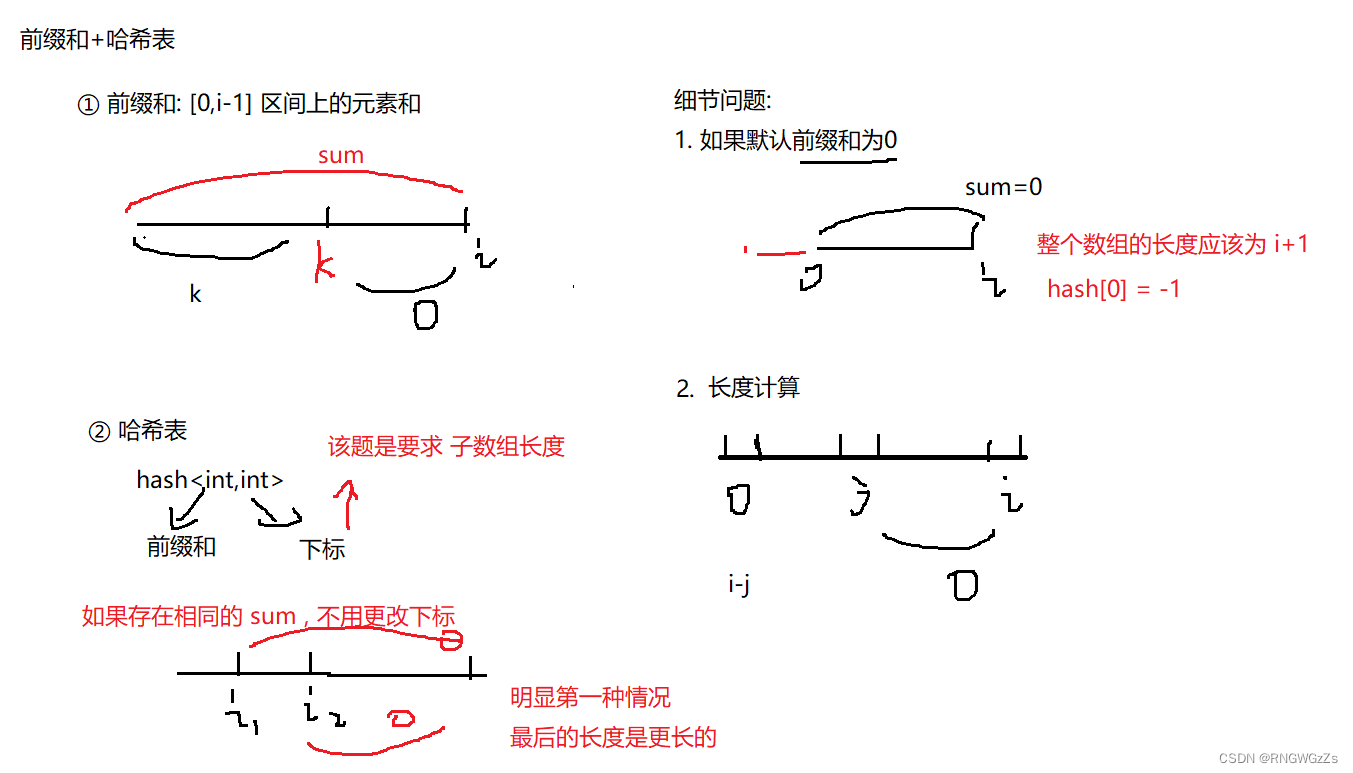
我们可以根据1,-1的性质,因为题目是要找到能够匹配相同数量的0,1数字。当我们将0替换为-1时,如果存在长度相同的0,1数对,那么它们的和为0。反过来,本题就是要找最长子数组元素和为0的长度。
(2) 算法原理
class Solution {
public:
int findMaxLength(vector<int>& nums) {
int n = nums.size();
unordered_map<int,int> hash;
hash[0] = -1;
int sum = 0;
int len = 0;
for(int i = 0; i < nums.size(); i++)
{
sum += nums[i] == 0 ? -1 : 1; // 计算前缀和
if(hash.count(sum)) len = max(len,i - hash[sum]);
else hash[sum] = i; // 存储下标
}
return len;
}
};8、矩阵区域和
(1) 题目解析
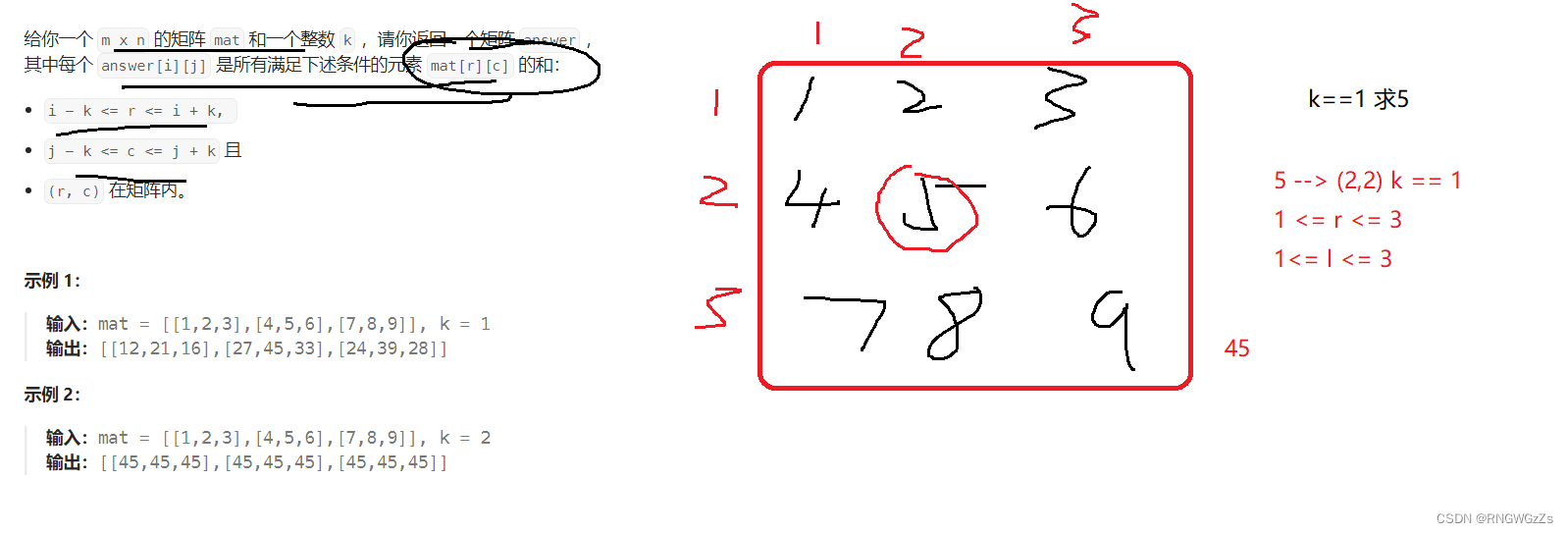
矩阵和同二维前缀和是相差无几的,都是求区域内的面积。例如上述例子,虽然是求整个矩阵的元素和,但是可以化解为从下标[1,1] 到 下标[3,3] 的前缀和矩阵。
(2) 算法原理
计算前缀和:
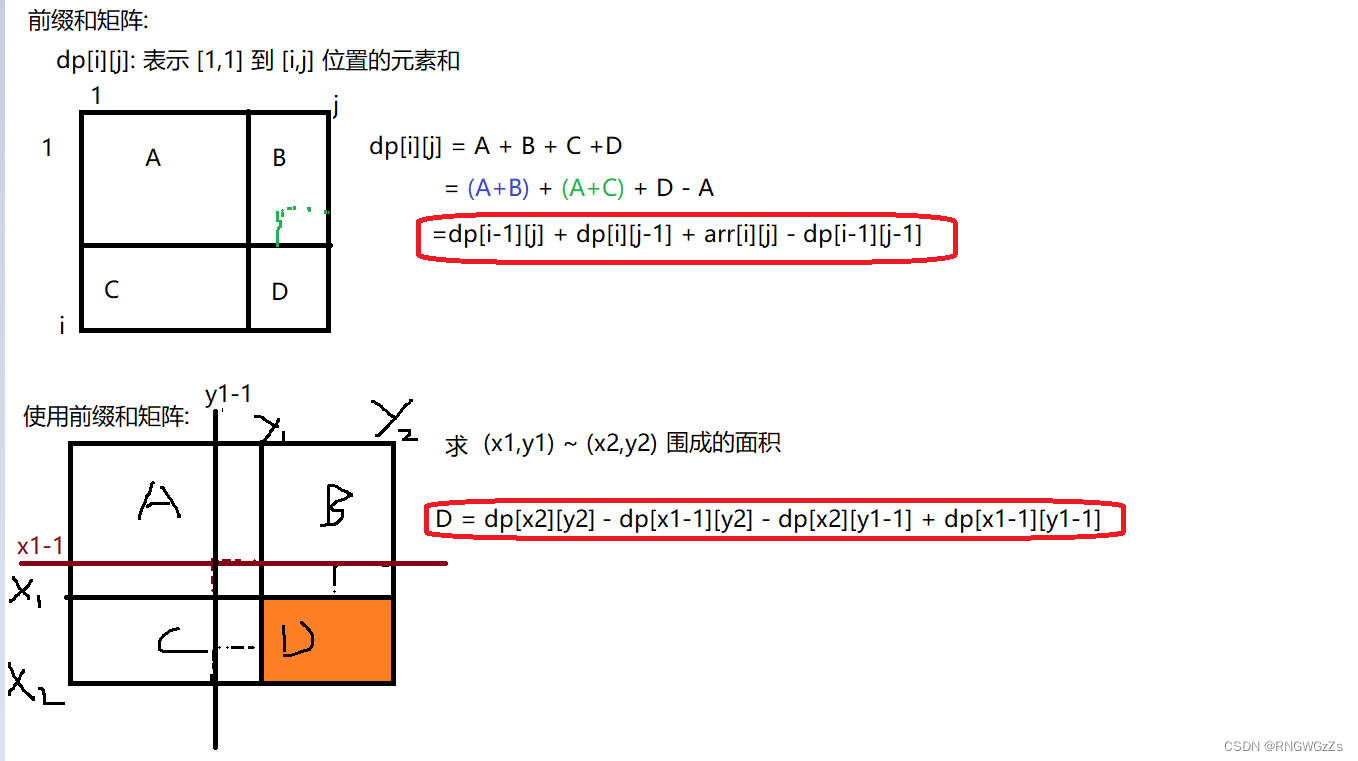
使用前缀和:
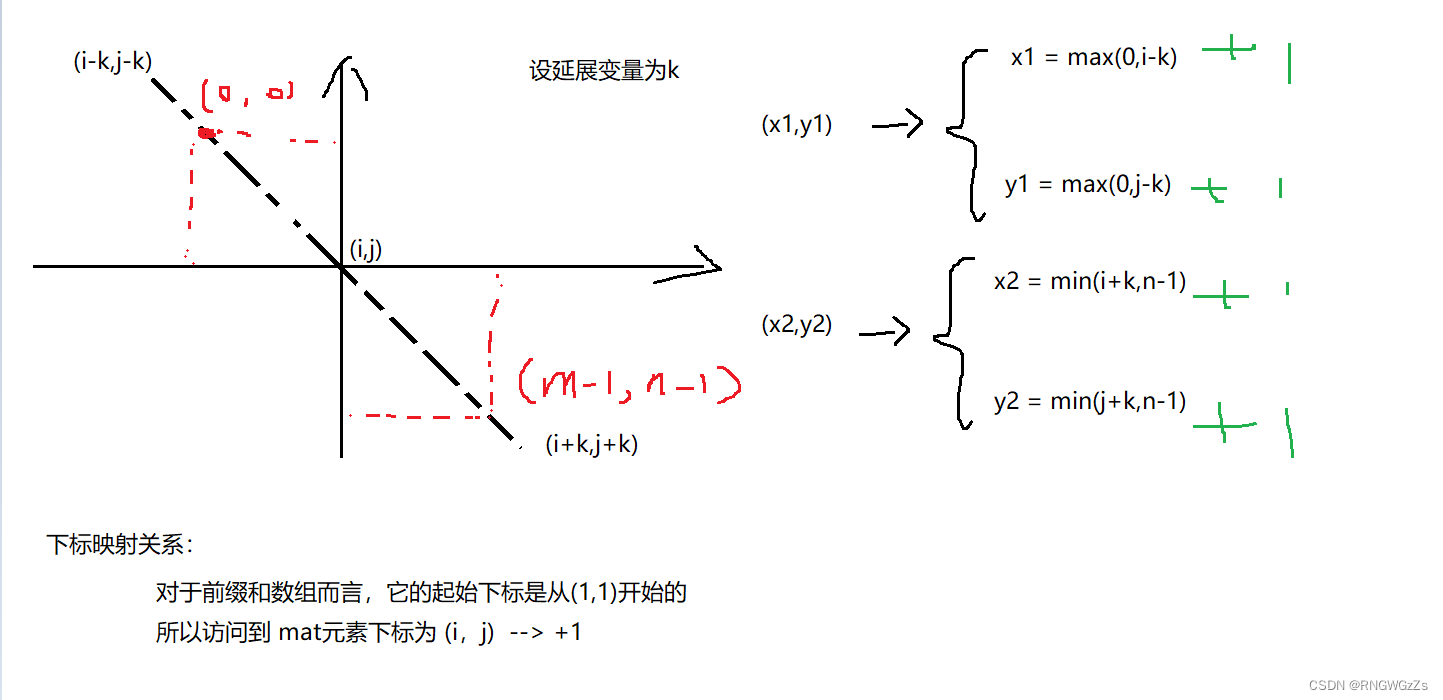
class Solution {
public:
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
int m = mat.size();
int n = mat[0].size();
// 初始化前缀和
vector<vector<int>> dp(m+1,vector<int>(n+1));
for(int i=1;i<=m;++i)
for(int j=1;j<=n;++j) dp[i][j] = dp[i-1][j] + dp[i][j-1] + mat[i-1][j-1] - dp[i-1][j-1];
// 使用前缀和
vector<vector<int>> ret(m,vector<int>(n));
for(int i=0;i<m;++i)
for(int j=0;j<n;++j)
{
int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;
int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;
ret[i][j] = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];
}
return ret;
}
};本篇到此结束,感谢你的阅读。
祝你好运,向阳而生~