本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

存在一个由 n 个节点组成的无向连通图，图中的节点按从 0 到 n - 1 编号。

给你一个数组 graph 表示这个图。其中，graph[i] 是一个列表，由所有与节点 i 直接相连的节点组成。

返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止，也可以多次重访节点，并且可以重用边。

示例 1：

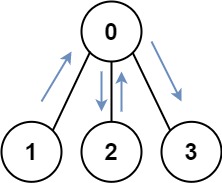
输入：graph = [[1,2,3],[0],[0],[0]]
输出：4
解释：一种可能的路径为 [1,0,2,0,3]

示例 2：

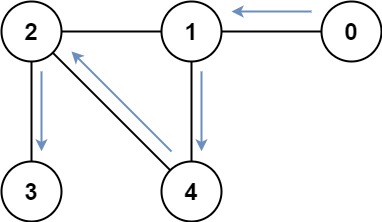
输入：graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
输出：4
解释：一种可能的路径为 [0,1,4,2,3]

提示：

• n == graph.length
• 1 <= n <= 12
• 0 <= graph[i].length < n
• graph[i] 不包含 i
• 如果 graph[a] 包含 b ，那么 graph[b] 也包含 a
• 输入的图总是连通图

---

解法1 状态压缩 + 广度优先搜索

由于题目需要我们求出「访问所有节点的最短路径的长度」，并且图中每一条边的长度均为 $1$ ，因此我们可以考虑使用广度优先搜索的方法求出最短路径。

在常规的广度优先搜索中，我们会在队列中存储节点的编号。对于本题而言，最短路径的前提是「访问了所有节点」，因此除了记录节点的编号以外，我们还需要记录每一个节点的经过情况。因此，我们使用三元组 $(u,mask,dist)$ 表示队列中的每一个元素，其中：

• $u$ 表示当前位于的节点编号；
• $mask$ 是一个长度为 $n$ 的二进制数，表示每一个节点是否经过。如果 $mask$ 的第 $i$ 位是 $1$ ，则表示节点 $i$ 已经过，否则表示节点 $i$ 未经过；
• $dist$ 表示到当前节点为止经过的路径长度。

这样一来，我们使用该三元组进行广度优先搜索，即可解决本题。初始时，我们将所有的 $(i,2^i,0)$ 放入队列，表示可以从任一节点开始。在搜索的过程中，如果当前三元组中的 $mask$ 包含 $n$ 个 $1$（即 $\text{mask}=2^n-1$ ），那么我们就可以返回 $dist$ 作为答案。

细节：为了保证广度优先搜索时间复杂度的正确性，即同一个节点 $u$ 以及节点的经过情况 $mask$ 只被搜索到一次，我们可以使用数组或者哈希表记录 $(u,mask)$ 是否已经被搜索过，防止无效的重复搜索。

class Solution {
public:
    int shortestPathLength(vector<vector<int>>& g) {
        int n = g.size();
        queue<tuple<int, int, int>> q;
        vector<vector<bool>> vis(n, vector<bool>(1 << n)); // [u,mask],避免重复遍历
        for (int i = 0; i < n; ++i) {
            q.emplace(i, 1 << i, 0);
            vis[i][1 << i] = true;
        }
        int ans = 0;
        while (!q.empty()) {
            auto [u, mask, dist] = q.front();
            q.pop();
            if (mask == (1 << n) - 1) {
                ans = dist;
                break;
            }
            // 搜索相邻的节点
            for (int v : g[u]) {
                // 将mask的第v位置1
                int maskV = mask | (1 << v);
                if (!vis[v][maskV]) {
                    q.emplace(v, maskV, dist + 1);
                    vis[v][maskV] = true;
                }
            }
        }
        return ans;
    }
};

复杂度分析：

• 时间复杂度：$O(n^2\cdot 2^n)$ 。常规的广度优先搜索的时间复杂度为 $O(n+m)$ ，其中 $n$ 和 $m$ 分别表示图的节点数和边数。本题中引入了 $mask$ 这一维度，其取值范围为 $[0,2^n)$ ，因此可以看成是进行了 $2^n$ 次常规的广度优先搜索。由于 $m$ 的范围没有显式给出，在最坏情况下为完全图，有 $O(n^2)=m$ ，因此总时间复杂度为 $O(n^2\cdot 2^n)$ 。
• 空间复杂度：$O(n\cdot 2^n)$ ，即为队列需要使用的空间。

---

解法2 预处理点对间最短路 + 状态压缩动态规划

由于题目中给定的图是连通图，那么我们可以计算出任意两个节点之间 $u,v$ 间的最短距离，记为 $d(u,v)$ 。这样一来，我们就可以使用动态规划的方法计算出最短路径。

对于任意一条经过所有节点的路径，它的某一个子序列（可以不连续）一定是 $0,1,\cdots ,n-1$ 的一个排列。我们称这个子序列上的节点为「关键节点」。在动态规划的过程中，我们也是通过枚举「关键节点」进行状态转移的。

我们用 $f[u][\text{mask}]$ 表示从任一节点开始到节点 $u$ 为止，并且经过的「关键节点」对应的二进制表示为 $mask$ 时的最短路径长度。由于 $u$ 是最后一个「关键节点」，那么在进行状态转移时，我们可以枚举上一个「关键节点」$v$ ，即：
$$f[u][\text{mask}]=\underset{v\in \text{mask},v\ne u}{\min }\{f[v][\text{mask}\backslash u]+d(v,u)\}$$

其中 $\text{mask}\backslash u$ 表示将 $mask$ 的第 $u$ 位从 $1$ 变为 $0$ 后的二进制表示。也就是说，「关键节点」$v$ 在 $mask$ 中的对应位置必须为 $1$ ，将 $f[v][\text{mask}\backslash u]$ 加上从 $v$ 走到 $u$ 的最短路径长度为 $d(v,u)$ ，取最小值即为 $f[u][mask]$ 。

最终的答案即为：$$\underset{u}{\min }f[u][2^n-1]$$
细节：当 $mask$ 中只包含一个 $1$ 时，我们无法枚举满足要求的上一个「关键节点」$v$ 。这里的处理方式与方法一中的类似：若 $mask$ 中只包含一个 $1$ ，说明我们位于开始的节点，还未经过任何路径，因此状态转移方程直接写为：
$$f[u][mask]=0$$
此外，在状态转移方程中，我们需要多次求出 $d(v,u)$ ，因此我们可以考虑在动态规划前将所有的 $d(v,u)$ 预处理出来。这里有两种可以使用的方法，时间复杂度均为 $O(n^3)$ ：

• 我们可以使用 $Floyd$ 算法求出所有点对之间的最短路径长度；
• 我们可以进行 $n$ 次广度优先搜索，第 $i$ 次从节点 $i$ 出发，也可以得到所有点对之间的最短路径长度。

class Solution {
public:
    int shortestPathLength(vector<vector<int>>& g) {
        int n = g.size();
        vector<vector<int>> d(n, vector<int>(n, n + 1));
        for (int i = 0; i < n; ++i) for (int j : g[i]) 
            d[i][j] = 1;
        // 使用floyd算法预处理出所有点对之间的最短路径长度
        for (int k = 0; k < n; ++k)
            for (int i = 0; i < n; ++i)
                for (int j = 0; j < n; ++j)
                    d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
        vector<vector<int>> f(n, vector<int>(1 << n, INT_MAX / 2));
        for (int mask = 1; mask < (1 << n); ++mask) {
            // 如果mask只包含一个1，即是2的幂
            if ((mask & (mask - 1)) == 0) {
                int u = __builtin_ctz(mask);
                f[u][mask] = 0; // 从某一点开始到u为止,经过的关键节点对应的二进制表示为mask时的最短路径长度
            } else {
                for (int u = 0; u < n; ++u) {
                    if (mask & (1 << u)) { // 如果经过了点u
                        for (int v = 0; v < n; ++v) { // 枚举上一个关键节点
                            if ((mask & (1 << v)) && u != v)
                                f[u][mask] = min(f[u][mask], f[v][mask ^ (1 << u)] 
                                    + d[v][u]);
                        }
                    }
                }
            }
        }
        int ans = INT_MAX;
        for (int u = 0; u < n; ++u) ans = min(ans, f[u][(1 << n) - 1]);
        return ans;
    }
};

复杂度分析：

• 时间复杂度：$O(n^2\cdot 2^n)$ 。状态的总数为 $O(n\cdot 2^n)$ ，对于每一个状态，我们需要 $O(n)$ 的时间枚举 $v$ 进行状态转移，因此总时间复杂度 $O(n^2\cdot 2^n)$ 。预处理所有 $d(u,v)$ 的时间复杂度为 $O(n^3)$ ，但其在渐近意义下小于 $O(n^2\cdot 2^n)$ ，因此可以忽略。
• 空间复杂度：$O(n\cdot 2^n)$ ，即为存储所有状态需要使用的空间。