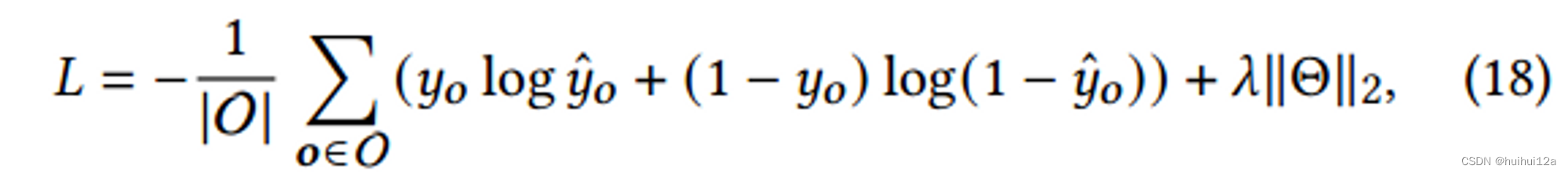Sequential Recommendation with Graph Neural Networks

1. 背景

序列推荐中存在问题：

• 长序列的用户行为反映了隐含的和嘈杂的偏好信号。用户可能会与许多带有隐式反馈的项目进行交互，比如点击和观看。与可以推断用户偏好的显式反馈(如喜欢和收藏夹)不同，单个隐式反馈无法反映用户偏好。
  用户可能会在大多数时候点击他们不感兴趣的项目，之后不会选择类似的项目进行交互。然而，这些记录将成为用户行为历史中的噪音，从而恶化了对他们真正兴趣的建模。
• 由于用户偏好的多样性，它们总是随着时间的推移而变化。正如我们所提到的，用户偏好是在变化的，不管是快是慢。给定一个时间点，一些首选项可能仍处于激活状态，而另一些可能已停用。
  因此，即使我们已经从隐式和噪声行为中提取了用户偏好，但如何建模它们在历史中的变化并估计当前激活的偏好仍然是一个挑战，这是推荐模型的核心。
  作者的想法：首先将松散的项目序列转换为紧密的项目-项目图，并设计一个关注图卷积网络，将弱信号收集到能准确反映用户偏好的强信号。然后，提出了一种动态图池化技术，该技术自适应地保留激活的核心偏好，以预测用户的下一个行为。

2. 模型

（1）先构造兴趣图：基于每个用户交互的商品items，计算两个item之间的相似性Mij，设置一个灵活的阈值，如果相似性大于阈值则两个节点之间有边。

（2）兴趣融合GNN

• 首先获取聚类注意力分数和query感知注意力分数

聚类注意分数：目标节点vi和其周围的k-hop邻居构成一个聚类，判断vi是否为聚类中心

query感知注意力分数，判断源节点vj和query节点vt的相关性。

将目标节点的聚类得分和源节点的查询得分相加作为源节点对目标节点的更新权值𝑗，注意力系数计算为：

其中邻居节点集合${\mathcal{N}}_i$包括节点i自身，${\alpha }_i$控制目标节点可以接收多少信息，${\beta }_j$控制的是源节点可以发送多少信息。

• 进行GNN
  
  （3）兴趣融提取图池化层

其实相当于把原始图中的节点分配到不同的簇中，再计算每个簇的嵌入向量，以及和query的相关性得分

首先获得分配矩阵S是n×m维，n是原始图中节点个数，m是簇的个数，矩阵中每个元素代表将原始图中节点分配给某个簇的概率：

表示获取第𝑖个节点被划分为𝑚集群的概率，然后计算每个簇的嵌入向量，以及和query的相关性得分：

（4）预测

• 从原始图获取图级表示，最简单的Readout就是求和
  

• 聚合后的粗图中嵌入进行顺序处理，因为原来的n个嵌入是有顺序的，想要聚合后的粗图多种也有顺序。使用带注意力的GRU，注意力就是${\gamma }^{\ast }$
  

• 预测。

将兴趣提取层的图级表示和兴趣进化层的进化输出作为用户当前的兴趣，并将它们与目标项嵌入连接起来，经过两层FNN：

2.1 Interest Graph Construction

2.1.1 Raw graph construction

此模块尝试为每个交互序列构建一个无向图 G = { V , E , A } \mathcal G = \{\mathcal V,\mathcal E,\mathcal A\} G={V,E,A},$\mathcal{V}$是交互的item的集合，目的是学习$\mathcal{E}$，即学习邻接矩阵A。

通过将每个用户的交互历史表示为图形，可以更容易地区分他/她的核心和外围兴趣。核心兴趣节点由于连接更多的相似兴趣，其度数高于外围兴趣节点，相似兴趣的频率越高，子图越密集、越大。

2.1.2 Node similarity metric learning

需要一个相邻节点相似的先验图，因此将图学习问题转化为节点相似度度量学习，与下游推荐任务联合训练。采用加权余弦相似度作为度量函数，并且使用多头度量，最后取均值，表示两个item嵌入向量的相似性：

2.1.3 Graph sparsification via 𝜀-sparseness

通常邻接矩阵应该是非负的，但从度量中计算出的余弦相似值在[-1,1]之间，简单的规范化它不会对图的稀疏性施加任何约束，并且可以产生一个完全连接的邻接矩阵，计算复杂的大，并且可能引入噪声，即不重要的边，因为不够稀疏，导致后续的图卷积不能关注图的最相关方面。
从𝑀中提取对称稀疏非负邻接矩阵，只考虑连接最重要的节点对。为了使提取阈值的超参数不敏感且不破坏图的稀疏性分布，采用了整个图的相对排序策略，即屏蔽(即设置为零)𝑀中小于非负阈值的那些元素。

2.2 Interest-fusion Graph Convolutional Layer

已经有可学习的兴趣图区分不同的兴趣，核心兴趣和外围兴趣分别形成大集群和小集群，不同类型的兴趣形成不同的集群，此外，为了将弱信号收集到能够准确反映用户偏好的强信号，需要在构建的图中聚合信息。

2.2.1 Interest fusion via graph attentive convolution

提出一个聚类和query感知的图关注卷积层，它可以感知用户在信息聚合过程中的核心兴趣(即位于聚类中心的item)和与查询兴趣相关的兴趣(即当前目标item)。

$E_{ij}$映射目标节点$v_i$在其邻居节点$v_j$上的重要性，进一步使用多头：

输入是一个节点嵌入矩阵 { h ⃗ 1 , h ⃗ 2 , . . . , h ⃗ n } , h ⃗ i ∈ R d \{\vec h_1,\vec h_2,...,\vec h_n\},\vec h_i \in \mathbb R^d {h 1​,h 2​,...,h n​},h i​∈Rd，其中𝑛为节点数(即用户交互序列的长度)，𝑑为每个节点的嵌入维数。该层产生一个新的节点嵌入矩阵 { h ⃗ 1 ′ , h ⃗ 2 ′ , . . . , h ⃗ n ′ } , h ⃗ i ′ ∈ R d ′ \{\vec h'_1,\vec h'_2,...,\vec h'_n\},\vec h'_i \in \mathbb R^{d'} {h 1′​,h 2′​,...,h n′​},h i′​∈Rd′

2.2.2 Cluster- and query-aware attention

为了在兴趣整合过程中增强重要信号，减弱噪声信号，提出了一种聚类和query感知的注意力机制。在休息传递过程中，利用注意力系数对边缘信息的权重进行重新分配，注意力机制考虑两个方面：
（1）认为target node $v_i$的邻居构成了一个cluster，判断target node是否是cluster的中心。
定义$v_i$的k-hop邻居是cluster的接受域，聚cluster中所有节点嵌入的平均${\vec{h}}_{i_c}$表示cluster的平均信息，为了识别目标节点是否为cluster的中心，使用目标节点嵌入及其cluster嵌入来计算以下关注分数：

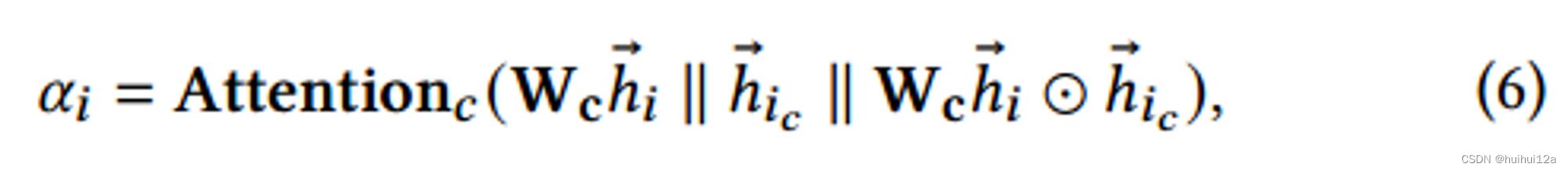
（2）学习source node和target node的嵌入之间的相关性
如果源节点与查询项的相关性更强，那么它在聚合中对目标节点的权重就更大。因为只有相关的行为才能在最终的预测中发挥作用：

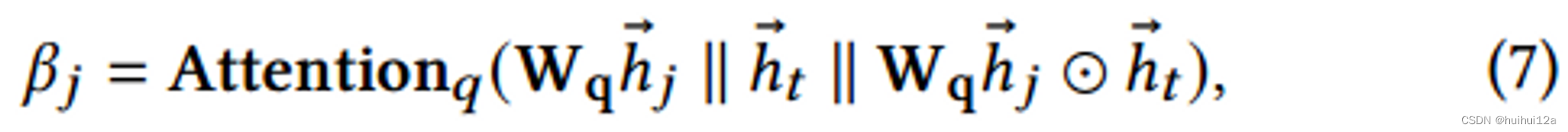
将目标节点的聚类得分和源节点的查询得分相加作为源节点对目标节点的更新权值𝑗，注意力系数计算为：

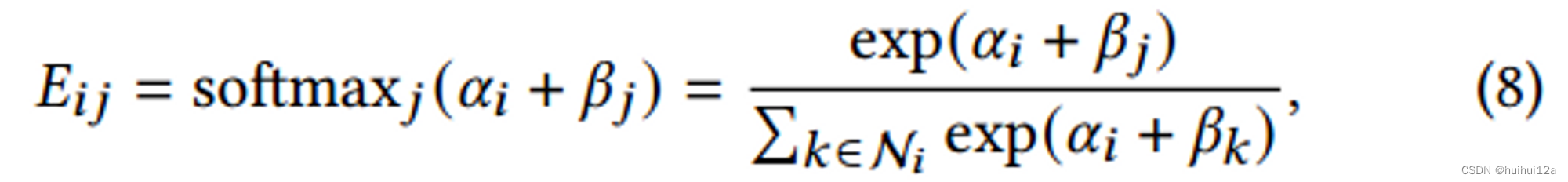
其中邻居节点集合${\mathcal{N}}_i$包括节点i自身，${\alpha }_i$控制目标节点可以接收多少信息，${\beta }_j$控制的是源节点可以发送多少信息。

2.3 Interest-extraction Graph Pooling Layer

池化的目的是对图进行合理的降采样。通过对所构造的图结构进行粗化，将松散兴趣转化为紧密兴趣，并保持其分布。

2.3.1 Interest extraction via graph pooling

为了得到池化图，需要一个聚类分配矩阵$S\in {\mathbb{R}}^{n\times m}$,给定原始图中的节点嵌入 { h ⃗ 1 ′ , h ⃗ 2 ′ , . . . , h ⃗ n ′ } \{\vec h'_1,\vec h'_2,...,\vec h'_n\} {h 1′​,h 2′​,...,h n′​}和节点的得分 { γ 1 , γ 2 , . . . γ n } \{\gamma_1,\gamma_2,...\gamma_n\} {γ1​,γ2​,...γn​}，聚类后粗化图的聚类嵌入和分数如下：

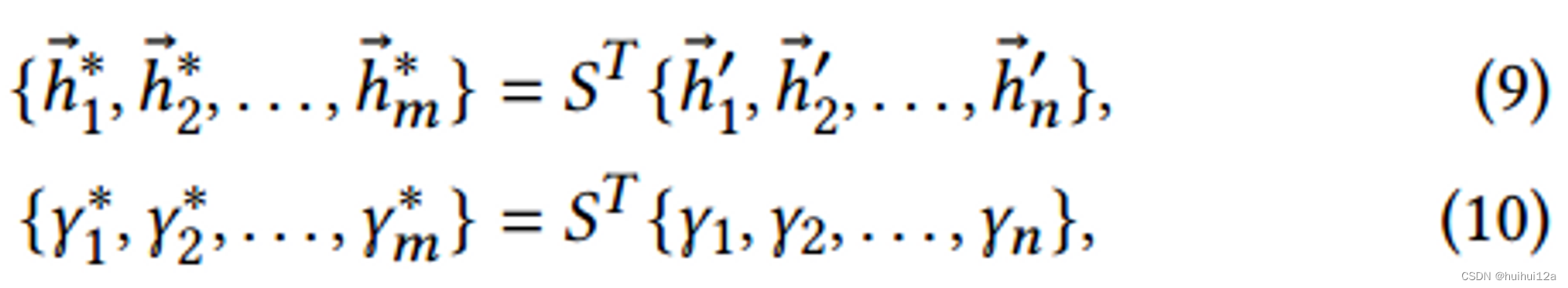
其中${\gamma }_i$是对${\beta }_i$的softmax，S为每个节点提供相应聚类的软分配。基于邻接矩阵和节点嵌入，通过标准消息传递和softmax函数得到分配映射的概率矩阵：

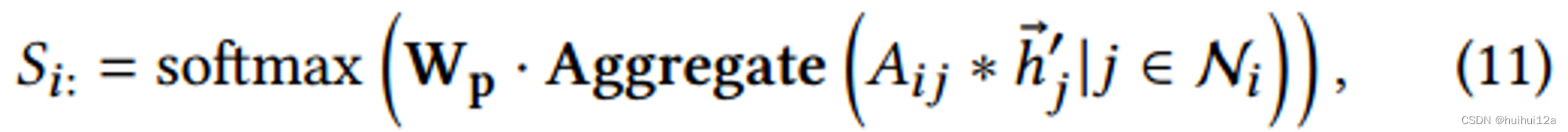
softmax函数用于获取第𝑖个节点被划分为𝑚集群的概率，可以通过$S^{T}AS$获得池化后，相当于聚类后的图的邻接矩阵$A^{\ast }$，确保集群间的连通性。当然也可以使用多层池化，得到分层聚类。

2.3.2 Assignment regularization

• Same maping regularization
  使连接强度较大的两个节点更容易映射到同一个集群:
  
  邻接矩阵A中各变量表示两个节点之间的连接强度，$S{S}^T$中的每个元素表示两个节点被划分到同一聚类的概率。
• Single affiliation regularization
  为了清晰地定义每个聚类的隶属关系，通过对熵进行如下正则化，使分配矩阵中的每一行𝑆i:趋近于一个one-hot向量:
  
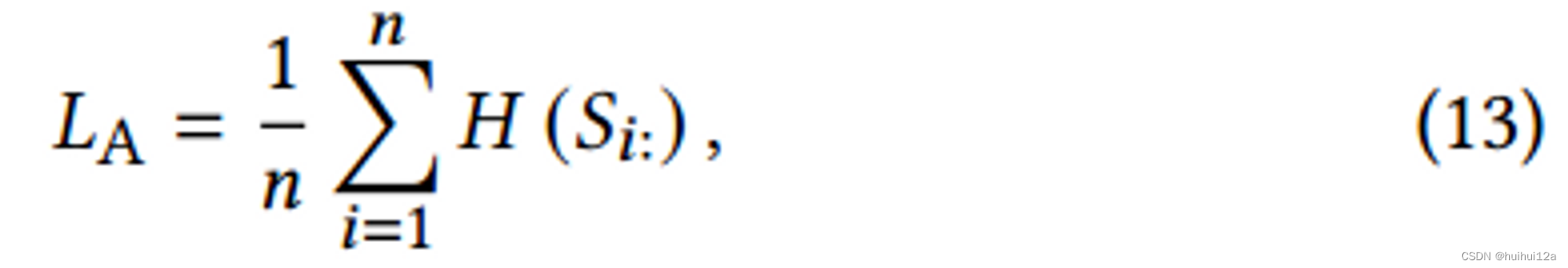
• Relative position regularization
  
  下游兴趣演化建模需要保持用户兴趣池化前后的时间顺序，因此，设计了一个位置正则化来保证池化过程中聚类之间的时间顺序：
  Pn是位置编码向量{1,2,…,n}，Pm是位置编码向量{1,2,…,m}。最小化L2范数使得𝑆中非零元素的位置更接近主对角线元素。直观地看，对于原序列中处于最前面位置的节点，其所分配的簇的位置索引倾向于在最前面。

2.3.3 Graph readout

已经得到了一个表示用户更强烈兴趣信号的紧密粗化图${\mathcal{G}}^{\ast }$,同时，对原始图$\mathcal{G}$进行加权读出，约束每个节点的重要性，在传播层前向计算后，对所有节点嵌入进行聚合，生成图级表示：

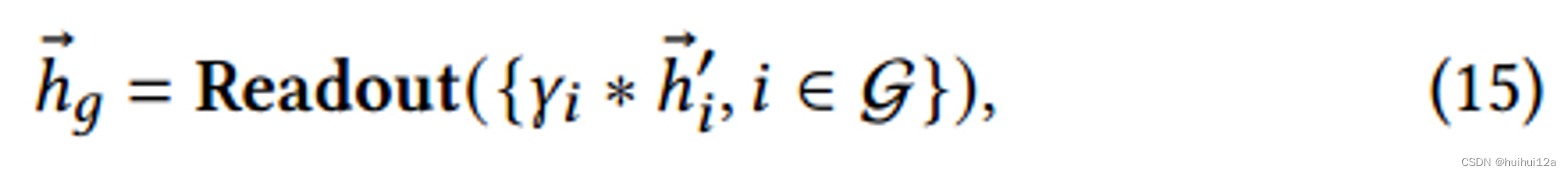
2.4 Prediction Layer

2.4.1 Interest evolution modeling

在外部环境和内部认知的共同影响下，用户的核心兴趣在不断演变。用户可能在一段时间对各种运动感兴趣，在另一段时间需要书籍。但是，仅使用上述读出操作，不考虑核心利益之间的演变，无疑会造成时间顺序的偏差。为了向兴趣的最终表示提供更多相关的历史信息，还需要考虑兴趣之间的时间顺序关系。

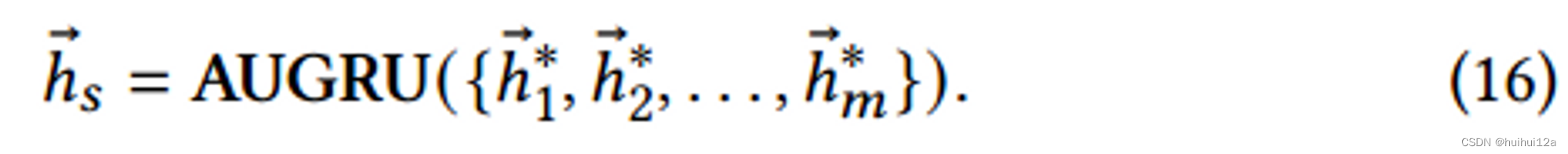
为了更好利用兴趣提取层中融合兴趣的重要性权值${\gamma }^{\ast }$，采用带注意力机制的GRU,AUGRU使用注意力分数${\gamma }^{\ast }$来缩放更新门的所有维度，结果表明，兴趣越不相关，对隐藏状态的影响越小。它更有效地避免了兴趣漂移的干扰，推动了相对兴趣的平稳演化

2.4.2 Prediction

将兴趣提取层的图级表示和兴趣进化层的进化输出作为用户当前的兴趣，并将它们与目标项嵌入连接起来，经过两层FNN：

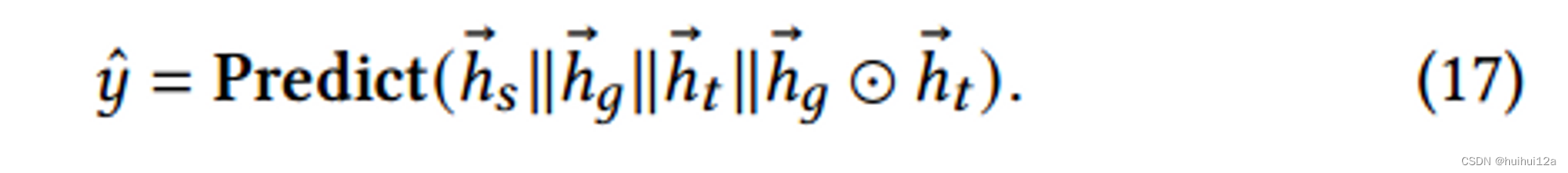
损失函数为：