文章目录
- 向量空间
- 向量及其性质
- 基与维数
- 向量的坐标运算
《线性代数的本质》 - 3blue1brown
高中数学A版选修4-2 矩阵与变换
《线性代数及其应用》(第五版)
《高等代数简明教程》- 蓝以中
向量空间
In the beginning Grant created the space. And Grant said, Let there be vector: and there was vector.
向量及其性质
三维几何空间中的一个有向线段称为向量(vector)。本文统一用 a , b , c , k , λ a,b,c,k,\lambda a,b,c,k,λ 表示标量,小写黑体字母 u , v , w , a , b , x \mathbf u,\mathbf v,\mathbf w,\mathbf a,\mathbf b,\mathbf x u,v,w,a,b,x 表示向量。
向量通常定义两种运算:加法和数乘。加法遵循三角形法则(平行四边形法则),数乘被称为缩放(scaling)。运算法则如下图
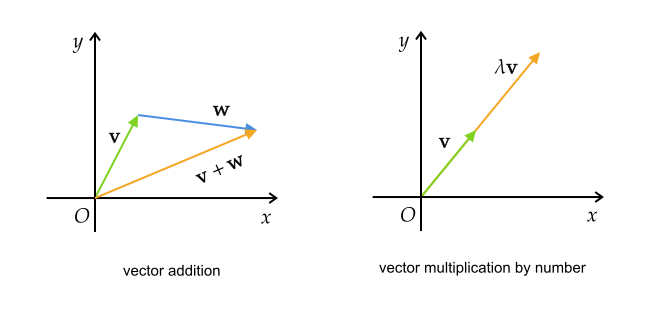
性质:根据向量的几何性质可证明向量的加法和数乘满足以下八条性质:
- 加法交换律: v + w = w + v \mathbf v+\mathbf w=\mathbf w+\mathbf v v+w=w+v
- 加法结合律: u + ( v + w ) = ( u + v ) + w \mathbf u+(\mathbf v+\mathbf w)=(\mathbf u+\mathbf v)+\mathbf w u+(v+w)=(u+v)+w
- 加法单位元: ∃ 0 ∈ V , 0 + v = v \exists 0\in V,\ 0+\mathbf v=\mathbf v ∃0∈V, 0+v=v
- 加法逆元: ∃ ( − v ) ∈ V , v + ( − v ) = 0 \exists (-\mathbf v)\in V,\ \mathbf v+(-\mathbf v)=0 ∃(−v)∈V, v+(−v)=0
- 数乘结合律: a ( b v ) = ( a b ) v a(b\mathbf v)=(ab)\mathbf v a(bv)=(ab)v
- 数乘分配律: a ( v + w ) = a v + a w a(\mathbf v+\mathbf w)=a\mathbf v+a\mathbf w a(v+w)=av+aw
- 数乘分配律: ( a + b ) v = a v + b v (a+b)\mathbf v=a\mathbf v+b\mathbf v (a+b)v=av+bv
- 数乘单位元: ∃ 1 ∈ F , 1 v = v \exists 1\in\mathbb F,\ 1\mathbf v=\mathbf v ∃1∈F, 1v=v
向量空间是三维几何空间向高维空间的推广。线性代数中,每个向量都以坐标原点为起点,那么任何一个向量就由其终点唯一确定。从而,向量和空间中的点一一对应。因此,空间也可以看成由所有向量组成的集合,并且集合中的元素可以进行加法和数乘运算。于是,便有了向量空间的抽象定义。
向量空间: 设 V V V 为 n n n 维向量的非空集合, F \mathbb F F 是一个数域,若 V V V 对于向量的加法和数乘两种运算封闭,那么称集合 V V V 为数域 F F F 上的向量空间(vector space)。所谓封闭是指
- ∀ v , w ∈ V , v + w ∈ V \forall\mathbf v,\mathbf w\in V,\ \mathbf v+\mathbf w\in V ∀v,w∈V, v+w∈V
- ∀ v ∈ V , c ∈ F , c v ∈ V \forall\mathbf v\in V, c\in F,\ c\mathbf v\in V ∀v∈V,c∈F, cv∈V
线性代数中的数域通常取全体实数,即 F = R \mathbb F=\R F=R。
例如: n n n维向量的全体生成实数域上的向量空间
R n = { x = ( x 1 , x 2 , ⋯ , x n ) ∣ x 1 , x 2 , ⋯ , x n ∈ R } \R^n=\{\mathbf x=(x_1,x_2,\cdots,x_n)\mid x_1,x_2,\cdots,x_n\in\R\} Rn={x=(x1,x2,⋯,xn)∣x1,x2,⋯,xn∈R}
子空间:设 U U U 是向量空间 V V V 的一个非空子集,如果 U U U中的线性运算封闭,则 U U U 也是向量空间,称为 V V V 的子空间。
基与维数
仿照解析几何的基本方法,建立一个坐标系,实现空间内的点与有序实数对一一对应,从而空间内的向量与有序实数对也一一对应,这样就可以用代数方法来研究向量的性质。
为方便建立空间的坐标系,先定义几个概念。
定义:取向量空间 V V V 内一个向量组 a 1 , a 2 , ⋯ , a r \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_r a1,a2,⋯,ar
- 向量 x 1 a 1 + x 2 a 2 + ⋯ + x r a r x_1\mathbf a_1+x_2\mathbf a_2+\cdots+x_r\mathbf a_r x1a1+x2a2+⋯+xrar 称为向量组的一个线性组合(linear combination)
- 向量组的所有线性组合构成的向量集称为由该向量组张成的空间,记作
span { a 1 , ⋯ , a n } = { x 1 a 1 + ⋯ + x n a n ∣ x 1 , ⋯ , x n ∈ R } \text{span}\{\mathbf a_1,\cdots,\mathbf a_n\}=\{x_1\mathbf a_1+\cdots+x_n\mathbf a_n\mid x_1,\cdots,x_n\in\R\} span{a1,⋯,an}={x1a1+⋯+xnan∣x1,⋯,xn∈R}
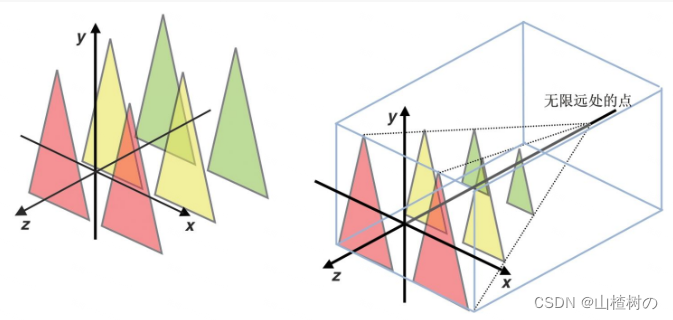
如下图,若 u , v ∈ R 3 \mathbf u,\mathbf v\in\R^3 u,v∈R3 不共线,则 span { u , v } \text{span}\{\mathbf u,\mathbf v\} span{u,v} 是 R 3 \R^3 R3中包含 u , v \mathbf u,\mathbf v u,v 和原点的平面,图示
 3. 当且仅当系数
x
1
=
x
2
=
⋯
=
x
r
=
0
x_1=x_2=\cdots=x_r=0
x1=x2=⋯=xr=0 时,线性组合为零
3. 当且仅当系数
x
1
=
x
2
=
⋯
=
x
r
=
0
x_1=x_2=\cdots=x_r=0
x1=x2=⋯=xr=0 时,线性组合为零
x
1
a
1
+
x
2
a
2
+
⋯
+
x
r
a
r
=
0
x_1\mathbf a_1+x_2\mathbf a_2+\cdots+x_r\mathbf a_r=0
x1a1+x2a2+⋯+xrar=0
则称向量组线性无关(linearly independence)。反之,如果存在不全为零的数使上式成立,则称向量组线性相关(linearly dependence)。
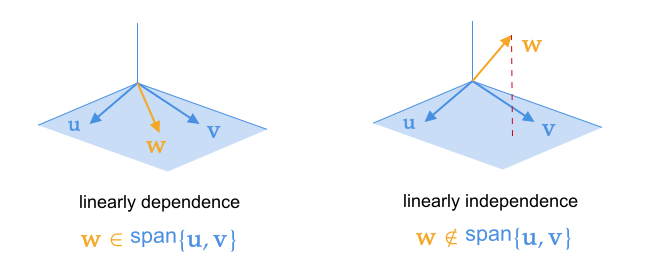
定理:若向量 v \mathbf v v 可由线性无关的向量组 a 1 , a 2 , ⋯ , a r \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_r a1,a2,⋯,ar 线性表示,则表示系数是唯一的。
证明:设向量
v
\mathbf v
v 有两组表示系数
b
=
k
1
a
1
+
k
2
a
2
+
⋯
+
k
r
a
r
b
=
l
1
a
1
+
l
2
a
2
+
⋯
+
l
r
a
r
\mathbf b=k_1\mathbf a_1+k_2\mathbf a_2+\cdots+k_r\mathbf a_r \\ \mathbf b=l_1\mathbf a_1+l_2\mathbf a_2+\cdots+l_r\mathbf a_r
b=k1a1+k2a2+⋯+krarb=l1a1+l2a2+⋯+lrar
则有
(
k
1
−
l
1
)
a
1
+
(
k
1
−
l
2
)
a
2
+
⋯
+
(
k
1
−
l
r
)
a
r
=
0
(k_1-l_1)\mathbf a_1+(k_1-l_2)\mathbf a_2+\cdots+(k_1-l_r)\mathbf a_r=0
(k1−l1)a1+(k1−l2)a2+⋯+(k1−lr)ar=0
因为
a
1
,
a
2
,
⋯
,
a
r
\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_r
a1,a2,⋯,ar 线性无关,故必有
k
1
−
l
1
=
k
1
−
l
1
=
⋯
=
k
1
−
l
1
=
0
k_1-l_1=k_1-l_1=\cdots=k_1-l_1=0
k1−l1=k1−l1=⋯=k1−l1=0
即表示系数是唯一的。
接下来,我们自然想用一组线性无关的向量来张成整个向量空间。
向量空间的基:张成向量空间 V V V的一个线性无关的向量集合称为该空间的一组基(basis)。基向量组所含向量的个数,称为向量空间 V V V的维数(dimension),记为 dim V \dim V dimV。
可以证明,向量空间的任意一组基的向量个数是相等的。
单由零向量组成的向量空间 { 0 } \{0\} {0}称为零空间。零空间的维数定义为零。
基定理: n n n 维向量空间的任意 n n n 个线性无关的向量构成空间的一组基。
向量的坐标运算
向量空间选定了基向量后,空间中全体向量的集合与全体有序实数组的集合之间就建立了一一 对应的关系。
坐标:设向量组
a
1
,
a
2
,
⋯
,
a
n
\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n
a1,a2,⋯,an 是线性空间
V
V
V 的一组基,则空间内任一向量
v
∈
V
\mathbf v\in V
v∈V 都可表示为基向量的唯一线性组合
v
=
x
1
a
1
+
x
2
a
2
+
⋯
+
x
n
a
n
\mathbf v=x_1\mathbf a_1+x_2\mathbf a_2+\cdots+x_n\mathbf a_n
v=x1a1+x2a2+⋯+xnan
有序数组
x
1
,
x
2
,
⋯
,
x
n
x_1,x_2,\cdots,x_n
x1,x2,⋯,xn 称为向量
v
\mathbf v
v 在基
a
1
,
a
2
,
⋯
,
a
n
\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n
a1,a2,⋯,an 下的坐标,一般记作
[
x
1
x
2
⋮
x
n
]
or
(
x
1
,
x
2
,
⋯
,
x
n
)
\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}\quad \text{or}\quad (x_1,x_2,\cdots,x_n)
x1x2⋮xn
or(x1,x2,⋯,xn)
类似于三维几何空间,由
n
n
n个有序数构成的向量称为
n
n
n维向量。

例:设 v 1 = [ 3 6 2 ] , v 2 = [ − 1 0 1 ] , x = [ 3 12 7 ] \mathbf v_1=\begin{bmatrix}3\\6\\2\end{bmatrix},\mathbf v_2=\begin{bmatrix}-1\\0\\1\end{bmatrix},\mathbf x=\begin{bmatrix}3\\12\\7\end{bmatrix} v1= 362 ,v2= −101 ,x= 3127 。判断 x \mathbf x x 是否在 H = span { v 1 , v 2 } H=\text{span }\{\mathbf v_1,\mathbf v_2\} H=span {v1,v2} 中,如果是,求 x \mathbf x x 相对于基向量 B = { v 1 , v 2 } B=\{\mathbf v_1,\mathbf v_2\} B={v1,v2} 的坐标。
解:如果
x
\mathbf x
x 在
H
=
span
{
v
1
,
v
2
}
H=\text{span }\{\mathbf v_1,\mathbf v_2\}
H=span {v1,v2} 中,则下列方程是有解的
c
1
[
3
6
2
]
+
c
2
[
−
1
0
1
]
=
[
3
12
7
]
c_1\begin{bmatrix}3\\6\\2\end{bmatrix}+c_2\begin{bmatrix}-1\\0\\1\end{bmatrix}=\begin{bmatrix}3\\12\\7\end{bmatrix}
c1
362
+c2
−101
=
3127
如果数
c
1
,
c
2
c_1,c_2
c1,c2存在,则它们是
x
\mathbf x
x 相对于
B
B
B 的坐标。由初等行变换得
[
3
−
1
3
6
0
12
2
1
7
]
→
[
1
0
2
0
1
3
0
0
0
]
\begin{bmatrix}\begin{array}{cc:c} 3&-1&3\\6&0&12\\2&1&7 \end{array}\end{bmatrix}\to \begin{bmatrix}\begin{array}{cc:c} 1&0&2\\0&1&3\\0&0&0 \end{array}\end{bmatrix}
362−1013127
→
100010230
于是,
x
\mathbf x
x 相对于
v
1
,
v
2
\mathbf v_1,\mathbf v_2
v1,v2 的坐标
v
B
=
[
3
2
]
\mathbf v_B=\begin{bmatrix}3\\2\end{bmatrix}
vB=[32]
有时为了区分坐标的基向量,向量 v \mathbf v v 在基 B = { b 1 , b 2 , ⋯ , b n } B=\{\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n\} B={b1,b2,⋯,bn} 下的坐标,记作 v B \mathbf v_B vB

建立了坐标之后, V V V中抽象的向量 v \mathbf v v 和 R n \R^n Rn中具体的数组 ( x 1 , x 2 , ⋯ , x n ) T (x_1,x_2,\cdots,x_n)^T (x1,x2,⋯,xn)T 实现了一一对应,并且向量的线性运算也可以表示为坐标的线性运算。
设
v
,
w
∈
V
\mathbf v,\mathbf w\in V
v,w∈V,有
v
=
v
1
a
1
+
v
2
a
2
+
⋯
+
v
n
a
n
w
=
w
1
a
1
+
w
2
a
2
+
⋯
+
w
n
a
n
\mathbf v=v_1\mathbf a_1+v_2\mathbf a_2+\cdots+v_n\mathbf a_n\\ \mathbf w=w_1\mathbf a_1+w_2\mathbf a_2+\cdots+w_n\mathbf a_n
v=v1a1+v2a2+⋯+vnanw=w1a1+w2a2+⋯+wnan
向量加法运算
v
+
w
=
(
v
1
+
w
1
)
a
1
+
(
v
2
+
w
2
)
a
2
+
⋯
+
(
v
n
+
w
n
)
a
n
\mathbf v+\mathbf w=(v_1+w_1)\mathbf a_1+(v_2+w_2)\mathbf a_2+\cdots+(v_n+w_n)\mathbf a_n
v+w=(v1+w1)a1+(v2+w2)a2+⋯+(vn+wn)an
即对应的坐标运算为
[
v
1
v
2
⋮
v
n
]
+
[
w
1
w
2
⋮
w
n
]
=
[
v
1
+
w
1
v
2
+
w
2
⋮
v
n
+
w
n
]
\begin{bmatrix}v_1\\ v_2\\ \vdots \\ v_n\end{bmatrix}+ \begin{bmatrix}w_1\\ w_2\\ \vdots \\ w_n\end{bmatrix}= \begin{bmatrix}v_1+w_1\\ v_2+w_2\\ \vdots \\ v_n+w_n\end{bmatrix}
v1v2⋮vn
+
w1w2⋮wn
=
v1+w1v2+w2⋮vn+wn
向量数乘运算
c
v
=
(
c
v
1
)
a
1
+
(
c
v
2
)
a
2
+
⋯
+
(
c
v
n
)
a
n
c\mathbf v=(cv_1)\mathbf a_1+(cv_2)\mathbf a_2+\cdots+(cv_n)\mathbf a_n
cv=(cv1)a1+(cv2)a2+⋯+(cvn)an
即对应的坐标运算为
c
[
v
1
v
2
⋮
v
n
]
=
[
c
v
1
c
v
2
⋮
c
v
n
]
c\begin{bmatrix}v_1\\ v_2\\ \vdots \\ v_n\end{bmatrix}= \begin{bmatrix}cv_1\\ cv_2\\ \vdots \\ cv_n\end{bmatrix}
c
v1v2⋮vn
=
cv1cv2⋮cvn
向量的坐标取值依托于坐标系的基向量。选取的基向量不同,其所对应的坐标值就不同。当然,基向量自身的坐标总是:
e
1
=
[
1
0
⋮
0
]
,
e
2
=
[
0
1
⋮
0
]
,
⋯
,
e
n
=
[
0
0
⋮
1
]
,
\mathbf e_1=\begin{bmatrix}1\\0\\\vdots\\0\end{bmatrix},\quad \mathbf e_2=\begin{bmatrix}0\\1\\\vdots\\0\end{bmatrix},\quad \cdots,\quad \mathbf e_n=\begin{bmatrix}0\\0\\\vdots\\1\end{bmatrix},\quad
e1=
10⋮0
,e2=
01⋮0
,⋯,en=
00⋮1
,
这种坐标形式通常称为标准向量组(或单位坐标向量组)。
总之,在 n n n维向量空间 V n V_n Vn 中任取一组基,则 V n V_n Vn 中的向量与 R n \R^n Rn 中的数组之间就有一一对应的关系,且这个对应关系保持线性组合(线性运算)的一一对应。接下来我们将默认使用标准坐标系:坐标原点为 O O O,基向量组为 e 1 , e 2 , ⋯ , e n \mathbf e_1,\mathbf e_2,\cdots,\mathbf e_n e1,e2,⋯,en 。后续将对向量实体和坐标不做区分。