WebGL透视投影

news2024/10/5 13:46:40

目录

透视投影

透视投影可视空间 

可视空间构造效果图

Matrix4.setPerspective（）

三角形与可视化空间的相对位置

示例代码

代码详解 

示例效果

投影矩阵的作用

透视投影矩阵对物体进行了两次变换

透视投影变换示意图

透视投影

在透视投影下，产生的三维场景看上去更是有深度感，更加自然，因为我们平时观察真实世界用的也是透视投影。在大多数情况下，比如三维射击类游戏中，我们都应当采用透视投影。

在下图的场景中，道路两边都有成排的树木。树应该都是差不多高的，但是在照片上，越远的树看上去越矮。同样，道路尽头的建筑看上去比近处的树矮，但实际上那座建筑比树高很多。这种“远处的东西看上去小”的效果赋予了照片深度感，或称透视感。我们的眼睛就是这样观察世界的。有趣的是，孩童的绘画往往会忽视这一点。

在正射投影的可视空间中，不管三角形与视点的距离是远是近，它有多大，那么画出来就有多大。为了打破这条限制，我们可以使用透视投影可视空间，它将使场景具有图上图那样的深度感。 

本例PerspectiveView使用了一个透视投影可视空间，视点在（0，0，5），视线沿着Z轴负方向。下图显示了程序的运行效果，以及程序的场景中各三角形的位置。

如上图（右）所示，沿着Z轴负半轴（也就是视线方向），在轴的左右侧各依次排列着3个相同大小的三角形，场景与本例第一张图中的道路和树木有一点相似。在使用透视投影矩阵后，WebGL就能够自动将距离远的物体缩小显示，从而产生上图（左）中的深度感。 

透视投影可视空间 

透视投影可视空间如下图所示。就像盒状可视空间那样，透视投影可视空间也有视点、视线、近裁剪面和远裁剪面，这样可视空间内的物体才会被显示，可视空间外的物体则不会显示。那些跨越可视空间边界的物体则只会显示其在可视空间内的部分。

可视空间构造效果图

不论是透视投影可视空间还是盒状可视空间，我们都用投影矩阵来表示它，但是定义矩阵的参数不同。Matrix4对象的setPerspective（）方法可用来定义透视投影可视空间。（WebGL矩阵变换库_山楂树の的博客-CSDN博客） 

Matrix4.setPerspective（）

定义了透视投影可视空间的矩阵被称为透视投影（perspective projection matrix）。

注意，第2个参数aspect是近裁剪面的宽高比，而不是水平视角（第1个参数是垂直视角）。比如说，如果近裁剪面的高度是100而宽度是200，那么宽高比就是2。

在本例中，各个三角形与可视空间的相对位置如下图所示。我们指定了near=1.0，far=100，aspect=1.0（宽度等于高度，与画面相同），以及fov=30.0。

三角形与可视化空间的相对位置

 

示例代码

var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_ViewMatrix;\n' +
  'uniform mat4 u_ProjMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_ProjMatrix * u_ViewMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  var canvas = document.getElementById('webgl');
  var gl = getWebGLContext(canvas);
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) return;
  // 设置顶点坐标和颜色，蓝色三角形在最前面
  var n = initVertexBuffers(gl);
  gl.clearColor(0, 0, 0, 1);
  var u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix');
  var u_ProjMatrix = gl.getUniformLocation(gl.program, 'u_ProjMatrix');
  var viewMatrix = new Matrix4();　// 视图矩阵
  var projMatrix = new Matrix4();  // 模型矩阵
  viewMatrix.setLookAt(0, 0, 5, 0, 0, -100, 0, 1, 0);  // 视点、被观察点、正方向
  projMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100); // 视角顶底面夹角、近裁面宽高比、near、far
  // 将视图和投影矩阵传递给u_ViewMatrix、u_ProjectMatrix
  gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);
  gl.uniformMatrix4fv(u_ProjMatrix, false, projMatrix.elements);
  gl.clear(gl.COLOR_BUFFER_BIT);
  gl.drawArrays(gl.TRIANGLES, 0, n);
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // 顶点坐标、颜色
    0.75,  1.0,  -4.0,  0.4,  1.0,  0.4, // 后面的绿色
    0.25, -1.0,  -4.0,  0.4,  1.0,  0.4,
    1.25, -1.0,  -4.0,  1.0,  0.4,  0.4, 
    0.75,  1.0,  -2.0,  1.0,  1.0,  0.4, // 中间的黄色
    0.25, -1.0,  -2.0,  1.0,  1.0,  0.4,
    1.25, -1.0,  -2.0,  1.0,  0.4,  0.4, 
    0.75,  1.0,   0.0,  0.4,  0.4,  1.0,  // 前面的蓝色
    0.25, -1.0,   0.0,  0.4,  0.4,  1.0,
    1.25, -1.0,   0.0,  1.0,  0.4,  0.4, 
    // 左侧有三个三角形
   -0.75,  1.0,  -4.0,  0.4,  1.0,  0.4, // 后面的绿色
   -1.25, -1.0,  -4.0,  0.4,  1.0,  0.4,
   -0.25, -1.0,  -4.0,  1.0,  0.4,  0.4, 
   -0.75,  1.0,  -2.0,  1.0,  1.0,  0.4, // 中间的黄色
   -1.25, -1.0,  -2.0,  1.0,  1.0,  0.4,
   -0.25, -1.0,  -2.0,  1.0,  0.4,  0.4, 
   -0.75,  1.0,   0.0,  0.4,  0.4,  1.0,  // 前面的蓝色
   -1.25, -1.0,   0.0,  0.4,  0.4,  1.0,
   -0.25, -1.0,   0.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 18; // 六个三角形18个顶点
  var vertexColorbuffer = gl.createBuffer();  
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);
  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);
  return n;
}

代码详解 

main（）函数中首先调用initVertexBuffers（）函数，向缓冲区对象中写入这6个三角形的顶点坐标和颜色数据（第26行），在这6个三角形中，右侧3个的数据从第44行开始，左侧3个的数据从第54行开始。而且，需要绘制的顶点的个数为18（第75行，6个三角形，3×6=18）。

接着，我们获取了着色器中视图矩阵和透视投影矩阵uniform变量的存储地址（第28行和第29行），并创建了两个对应的矩阵对象（第30和第31行）。

然后，我们计算了视图矩阵（第32行），视点设置在（0，0，5），视线为Z轴负方向，上方向为Y轴正方向。最后，我们按照金字塔状的可视空间建立了透视投影矩阵（第33行）。 

其中，第2个参数aspect宽高比（近裁剪面的宽度与高度的比值）应当与＜canvas＞保持一致，我们根据＜canvas＞的width和height属性来计算出该参数，这样如果＜canvas＞的大小发生变化，也不会导致显示出来的图形变形。 

接下来，将准备好的视图矩阵和透视投影矩阵传给着色器中对应的uniform变量（第35和第36行）。最后将三角形绘制出来（第38行），就获得了如下图所示的效果。

示例效果

到目前为止，还有一个重要的问题没有完全解释，那就是矩阵为什么可以用来定义可视空间。接下来，我们尽量避开其中复杂的数学过程，稍做一些探讨。

投影矩阵的作用

首先看一下本例的运行效果如上图，可以看到：运用透视投影矩阵后，场景中的三角形有了两处变化

透视投影矩阵对物体进行了两次变换

首先，距离较远的三角形看上去变小了；其次，三角形被不同程度地平移以贴近中心线（即视线），使得它们看上去在视线的左右排成了两列。实际上，如下图（左）所示，这些三角形的大小是完全相同的，透视投影矩阵对三角形进行了两次变换：（1）根据三角形与视点的距离，按比例对三角形进行了缩小变换；（2）对三角形进行平移变换，使其贴近视线，如下图右所示。经过了这两次变换之后，就产生了上图0那张照片中的深度效果。

透视投影变换示意图

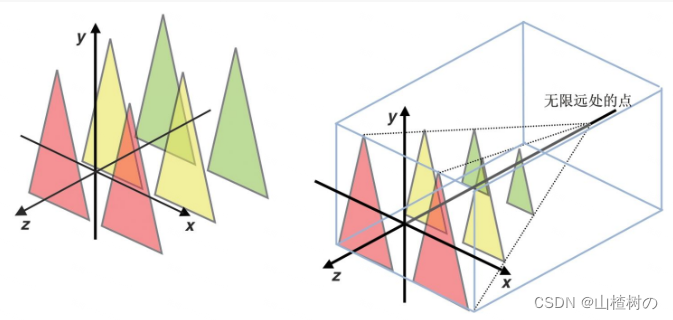
这表明，可视空间的规范（对透视投影可视空间来说，就是近、远裁剪面，垂直视角，宽高比）可以用一系列基本变换（如缩放、平移）来定义。Matrix4对象的setPerspective（）方法自动地根据上述可视空间的参数计算出对应的变换矩阵。

换一个角度来看，透视投影矩阵实际上将金字塔状的可视空间变换为了盒状的可视空间，这个盒状的可视空间又称规范立方体（Canonical View Volume），如上图（右）所示。

注意，正射投影矩阵不能产生深度感。正射投影矩阵的工作仅仅是将顶点从盒状的可视空间映射到规范立方体中。顶点着色器输出的顶点都必须在规范立方体中，这样才会显示在屏幕上。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1012101.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

华为云云耀云服务器L实例评测｜拉取创建canal镜像配置相关参数 搭建canal连接MySQL数据库 spring项目应用canal初步

华为云云耀云服务器L实例评测｜拉取创建canal镜像配置相关参数 搭建canal连接MySQL数据库 spring项目应用canal初步

前言 最近华为云云耀云服务器L实例上新，也搞了一台来玩，本篇博客介绍如何在华为云上部署canal的docker镜像，以及在spring项目中的初步应用。 其他相关的华为云云耀云服务器L实例评测文章列表如下： 初始化配置SSH连接 & 安装…
阅读更多...
IntelliJ IDEA使用_常用快捷键（windows版）

IntelliJ IDEA使用_常用快捷键（windows版）

文章目录 版本说明搜索操作层级关系查看光标选择代码定位代码操作Git操作编辑器操作 版本说明 当前的IntelliJ IDEA 的版本是2021.2.2（下载IntelliJ IDEA） ps：不同版本一些图标和设置位置可能会存在差异，但应该大部分都差不多。…
阅读更多...
C++ PrimerPlus 复习 第四章 复合类型（上）

C++ PrimerPlus 复习 第四章 复合类型（上）

第一章 命令编译链接文件 make文件 第二章 进入c 第三章 处理数据 第四章 复合类型 （上） 文章目录 创建和使用数组；**声明语句中初始化数组元素。****使用大括号的初始化（列表初始化）** 字符串创建和使用C风格字符…
阅读更多...
好用免费的链接转二维码

好用免费的链接转二维码

能把链接等转成二维码的形式 ，并且是完全免费的 ，超级好用：草料网址二维码生成器 https://cli.im/url?3f07d81d705e31db2dcde5ca2feeece8 测试了博客的链接转成了二维码 ，很好用
阅读更多...
（入门向）面向萌新的算法比赛入门指南

（入门向）面向萌新的算法比赛入门指南

什么是算法 算法是指解决问题或完成特定任务的一系列明确指令或步骤集合。它是一个定义良好、逐步执行的操作序列，用于将输入转换为输出。算法可用于计算、数据处理、自动化控制、问题解决等各个领域。 算法通常由一系列简单的操作组成，这些操作可以是…
阅读更多...
Java基于SpringBoot的逍遥大药房管理平台

Java基于SpringBoot的逍遥大药房管理平台

博主介绍：✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 大家好，我是程序员徐师兄、今天给大家谈谈基于android的app开发毕设题目，以及基于an…
阅读更多...
GIS前端编程—视频展示

GIS前端编程—视频展示

GIS前端编程—视频展示 视频展示1. 互联网公共地图服务开放平台2. 开源GIS服务平台 得益于互联网的快速发展，WebGIS发展迅猛，其开发工具与开发平台也呈现出百花齐放之势。目前，涌现出了大量的WebGIS二次开发产品。在互联网方向上，…
阅读更多...
【Springboot】整合kafka

【Springboot】整合kafka

目录 安装zookeeperjdk安装zookeeper安装 安装kafka（非集群）springboot项目整合配置 安装zookeeper jdk安装 环境准备：CentOS7，jdk1.8 步骤如下： 下载自己需要的版本 这里使用的jdk1.8，获取链接如下 链接…
阅读更多...
Maxwell 概述、安装、数据同步【一篇搞定】！

Maxwell 概述、安装、数据同步【一篇搞定】！

文章目录 什么是 Maxwell？Maxwell 输出格式Maxwell 工作原理Maxwell 安装Maxwell 历史数据同步Maxwell 增量数据同步 什么是 Maxwell？ Maxwell 在大数据领域通常指的是一个用于数据同步和数据捕获的开源工具，由美国 Zendesk 开源&#xff0c…
阅读更多...
千巡翼X1协调转弯功能

千巡翼X1协调转弯功能

近年来，随着技术的飞速发展，无人机航测已成为现代测绘领域的一项重要应用。 无人机的出现极大地提高了航测的效率和精度，极大地减少了人力资源的投入。通过搭载各种高精度的航测仪器和传感器，无人机可以在短时间内完成大面积的航…
阅读更多...
使用vscode以16进制方式查看bin文件内容

使用vscode以16进制方式查看bin文件内容

简介 方便对bin文件内容进行分析。 使用 VSCODE：插件下载 Hex Editor,下载完后使用vscode打开bin文件。 使用快捷键CtrlShiftP， 并在上方命令框输入>hex 选择 结果如下
阅读更多...
微信小程序隐私授权

微信小程序隐私授权

微信开发者平台新公告：2023年9月15之后，隐私协议将被启用，所以以后的小程序都要加上隐私协议的内容提示用户， 首先设置好隐私协议的内容，登录小程序的开发者后台，在设置--》服务内容声明--》用户隐私保护指…
阅读更多...
前端JavaScript入门到精通，javascript核心进阶ES6语法、API、js高级等基础知识和实战 —— JS基础（一）

前端JavaScript入门到精通，javascript核心进阶ES6语法、API、js高级等基础知识和实战 —— JS基础（一）

ﻌﻌﻌﻌ♡‎ﻌﻌﻌﻌ♡‎‎ﻌﻌﻌﻌ♡‎ﻌﻌﻌﻌ♡ﻌﻌﻌﻌ…
阅读更多...
OPC HDA扫盲

OPC HDA扫盲

目录 1 基本概念 1.1 历史数据服务器类型 1.2 数据源 1.3 对象和接口概述 1.4 所需接口定义 1.5 可选接口定义 1.6 定义 1.7 边界值和时域 2 HDA聚合 2.1 生成间隔 2.2 数据类型 2.3 数据质量 3 聚合示例 3.1 示例数据 3.2 内插（INTERPOLATIVE&#x…
阅读更多...
构造与析构

构造与析构

在类的声明中，构造函数和析构函数是一类特殊的函数：由系统自动执行，在程序中不可显示地调用它们。 构造函数 作用：建立对象时对对象的数据成员进行初始化 特点： 构造函数是与类同名的特殊成员函数，没有…
阅读更多...
Xamarin.Android实现App内版本更新

Xamarin.Android实现App内版本更新

目录 1、具体的效果2、代码实现2.1 基本原理2.2 开发环境2.3 具体代码2.3.1 基本设置2.3.2 系统的权限授予2.3.3 进度条的layout文件2.3.4 核心的升级文件 3、代码下载4、知识点5、参考文献 1、具体的效果 有事需要在程序内集成自动更新的功能，网上找了下&#xff…
阅读更多...
【ARM AMBA AXI 入门 11 - AXI 总线 AWCACHE 和 ARCACHE 介绍】

【ARM AMBA AXI 入门 11 - AXI 总线 AWCACHE 和 ARCACHE 介绍】

文章目录 1.1 AXI 传输事务属性1.1.1 slave type1.1.2 系统级缓存 1.2 Memory Attributes1.2.1 Bufferable，AxCACHE[0]1.2.2 Modifiable, AxCACHE[1]1.2.3 cache-allocate 1.3 Memory types 转自：https://zhuanlan.zhihu.com/p/148813963 如有侵权请联系…
阅读更多...
学习记忆——英语篇

学习记忆——英语篇

文章目录 英语字母形象起源右脑记忆单词的原则四大步骤第一步：摄取信息第二步：处理信息第三步：储存信息第四步：提取信息 训练例子字母形象训练 右脑记忆单词5大方法字源法编码法字母编码法字母组合编码法 拼音法全拼法拼音组合 熟…
阅读更多...
前K个高频单词-c++实现

前K个高频单词-c++实现

692. 前K个高频单词 - 力扣（LeetCode） 给定一个单词列表 words 和一个整数 k ，返回前 k 个出现次数最多的单词。 返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率， 按字典顺序 排序。 示例 1&#xff…
阅读更多...
关于Linux服务器.sh文件启动问题

关于Linux服务器.sh文件启动问题

问题描述 在linux服务器上使用文本编辑（并非vim操作）对.sh脚本文件进行修改后无法启动，显示’\r’识别错误等。 错误如下： 错误原因 因为.sh文件在经过这种编辑后格式产生了错误，由unix转为了doc格式，需…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023