题目链接:位运算、递推与递归、前缀和、差分、二分 - Virtual Judge (vjudge.net)
A.洛谷 - P2280

样例输入:
2 1
0 0 1
1 1 1
样例输出:
1分析:这道题先用二维前缀和处理一下地图,这样我们就可以在O(1)的复杂度内求取一个区域内的价值和,由于炸弹的爆破范围是固定的,所以我们只需要枚举矩形的一个端点即可唯一确定该区域,枚举复杂度为地图的大小,这样就可以通过本题了。
需要注意的是本题给的内存是131072kb,那么就能够开131072*1024B/4=33554432个int型变量,那么发现这个只允许我们开一个5000*5000的二维数组,所以我们就必须要省掉一个数组,我们可以省掉原数组,直接在前缀和数组上进行操作。
//一定要注意内存问题
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=5e3+10;
int s[N][N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int x,y,val;
scanf("%d%d%d",&x,&y,&val);
s[x+1][y+1]+=val;//为了防止越界这里进行一个偏移
}
for(int i=1;i<N;i++)
for(int j=1;j<N;j++)
s[i][j]=s[i][j]+s[i-1][j]+s[i][j-1]-s[i-1][j-1];
int ans=0;
for(int i=m;i<N;i++)
for(int j=m;j<N;j++)
ans=max(ans,s[i][j]-s[i-m][j]-s[i][j-m]+s[i-m][j-m]);
printf("%d",ans);
return 0;
}B.洛谷 - P1028
样例输入:
6
样例输出:
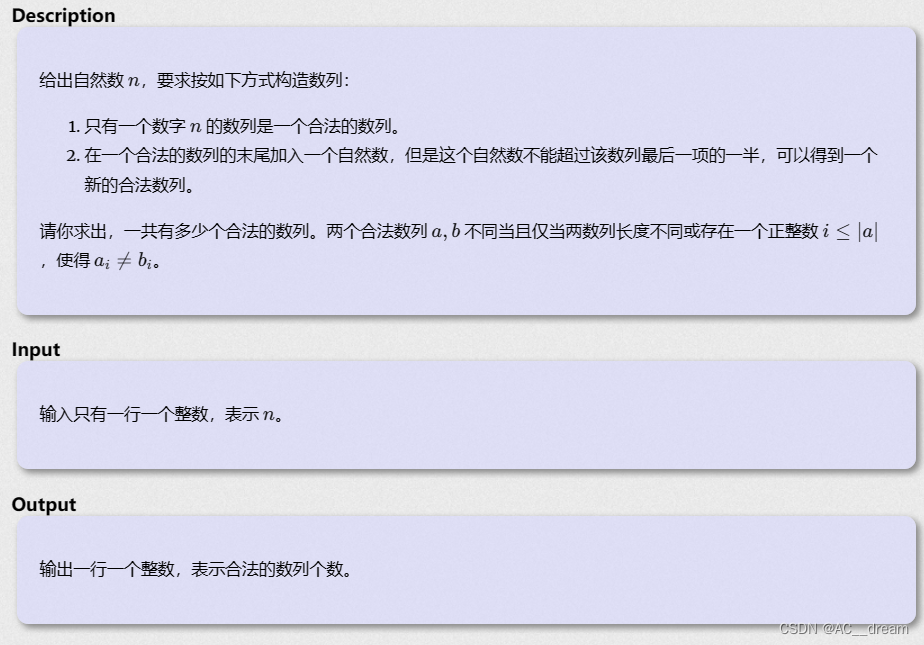
6分析:设f[i]表示以i作为开头能够扩展的最大合法序列数量,我们可以直接由f[0~(i/2)]递推过来,因为我们第一个位置放置i,那么第二个位置可以放0~i/2的任意数,所以就有,利用这个递推公式我们就可以求出来f[n],其中初始条件为f[0]=0
这道题也可以直接搜索,加一个记忆化,下面会附上两种方法的代码:
递推:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e3+10;
long long f[N];//f[i]表示以i作为开头能够扩展的最大合法序列数量
int main()
{
int n;
cin>>n;
f[0]=1;
for(int i=1;i<=n;i++)
for(int j=0;j<=i/2;j++)//枚举下一位是j
f[i]+=f[j];
printf("%d",f[n]);
return 0;
}记忆化搜索:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e3+10;
long long f[N];//f[i]表示以i作为开头能够扩展的最大合法序列数量
long long dfs(int x)//求取以x作为开头能够扩展的最大合法序列数量
{
if(f[x]!=-1) return f[x];
int ans=0;
for(int i=0;i<=x/2;i++)//枚举下一位是i
ans+=dfs(i);
f[x]=ans;//保存一下答案
return ans;
}
int main()
{
int n;
cin>>n;
f[0]=1;
for(int i=1;i<=n;i++) f[i]=-1;
printf("%d",dfs(n));
return 0;
}C.POJ - 3122

简化题意:一个人有n块蛋糕和f个朋友,接下来给出n块蛋糕的半径,每块蛋糕的高都是1.现在要将这n块蛋糕分给他自己以及他的f个朋友,保证每个人的蛋糕是一整块蛋糕上的,也就是说不能是由几块小蛋糕拼接而成的,而且每个人的蛋糕体积要相同,现在问每个人获得的蛋糕体积最大为多少?
样例输入:
3
3 3
4 3 3
1 24
5
10 5
1 4 2 3 4 5 6 5 4 2样例输出:
25.1327
3.1416
50.2655分析:这道题目我们直接二分每个人分得的蛋糕体积即可,对于每一个体积x,我们只需要计算每块蛋糕所能够划分出体积为x的蛋糕的份数和即可,注意是下取整,然后拿划分出的总数量和f+1进行比较,如果小于f+1说明蛋糕不够分,也就是我们枚举的体积偏大,否则就说明枚举体积偏小,继续增大x。
圆周率我们可以直接用acos(-1)来求,设置一个合适的二分精度即可。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
#define pi acos(-1)
const int N=1e4+10;
int r[N];
int n,f;
bool check(double v)
{
int cnt=0;
for(int i=1;i<=n;i++)
cnt+=(int)(pi*r[i]*r[i]/v);
return cnt>=f;
}
int main()
{
int T;
cin>>T;
while(T--)
{
scanf("%d%d",&n,&f);
for(int i=1;i<=n;i++)
scanf("%d",&r[i]);
f++;//注意分为f+1份
double l=0,r=999999999;
while(r-l>1e-6)
{
double mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
printf("%.4lf\n",l);
}
return 0;
} D.洛谷 - P3406
样例输入:
9 10
3 1 4 1 5 9 2 6 5 3
200 100 50
300 299 100
500 200 500
345 234 123
100 50 100
600 100 1
450 400 80
2 1 10样例输出:
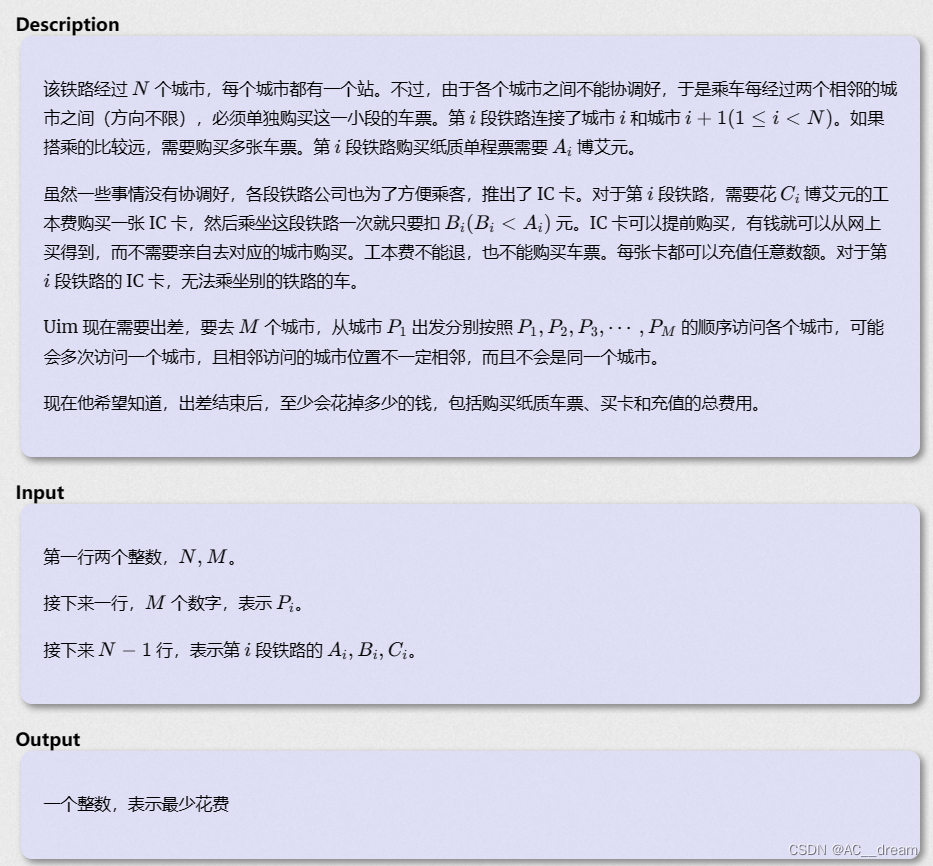
6394分析:我们可以分别考虑每一段的车票购买方式,要么就全部都购买纸质单程票,要么就买IC卡,任意两段的车票购买方式都是互不影响的,所以购买方式主要取决于该段一共需要经过多少次,如果经过的次数足够多,那么买IC卡会相对划算一些,否则就直接买纸质单程票即可。所以问题现在转化为求取每一段的经过次数,由于当前站和下一站不一定是相邻的,所以这相当于对一个区间进行修改,所以我们就可以转化为差分来进行区间修改。最后对于每一段我们都可以计算出该段的经过次数,然后直接分别计算两种方式的花费,取一个最小值即可。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e5+10;
int a[N];
int d[N];//记录差分数组
struct node{
long long a,b,c;
}p[N];//p[i]记录从第i个点到第i+1个点之间的铁路的花费
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++)
scanf("%d",&a[i]);
for(int i=1;i<n;i++)
scanf("%lld%lld%lld",&p[i].a,&p[i].b,&p[i].c);
for(int i=2;i<=m;i++)
{
int mi=min(a[i],a[i-1]);
int mx=max(a[i],a[i-1]);
d[mi]++;d[mx]--;
}
long long ans=0;
for(int i=1;i<n;i++)
{
d[i]+=d[i-1];//恢复为原数组
ans+=min(d[i]*p[i].a,p[i].c+d[i]*p[i].b);
}
printf("%lld\n",ans);
return 0;
}
E.洛谷 - P1164

样例输入:
4 4
1 1 2 2
样例输出:
3
分析:这道题目类似于01背包问题。
设f[i][j]表示考虑前i种菜后花费j元的方案数,对于第i种菜我们可以选择买或者不买,如果选择不买,那么有f[i-1][j]种情况,因为第i种菜没有买,那么相当于买前i-1种菜花费了j元,如果要是选择买,首先需要满足j是大于第i份菜的价格的,在满足这个条件的基础上有f[i-1][j-a[i]]种情况,因为一共花费了j元,第i种菜花费了a[i]元,那么前i-1种菜就花费了j-a[i]元,那么f[i][j]就是这两种情况的加和。按照这个方法递推即可。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=103,M=10003;
int a[N];
int f[N][M];//f[i][j]表示考虑前i种菜后花费j元的方案数
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
f[0][0]=1;
for(int i=1;i<=n;i++)
for(int j=0;j<=m;j++)
if(j<a[i]) f[i][j]=f[i-1][j];//当前的钱不够买第i种菜品
else f[i][j]=f[i-1][j]+f[i-1][j-a[i]];//当前的钱够买第i种菜品,所以有买或者不买两种选择
printf("%d\n",f[n][m]);
return 0;
} F.POJ - 3104

简化题意:现在有n件衣服,接下来给出n件衣服的含水量,在自然情况下每件衣服每秒钟会蒸发1单元的水分,现在有一台洗衣机,每秒可使得一件衣服的含水量减少k单元。问至少需要多长时间可以使得所有衣服的含水量减至0.
样例输入:
sample input #1
3
2 3 9
5
sample input #2
3
2 3 6
5样例输出:
sample output #1
3
sample output #2
2分析:题目中给出洗衣机每秒会使得一件衣服的含水量减少k单元,那么也就是每秒比不用洗衣机多减少k-1单元的水分,我们可以直接二分蒸干所需时间t,然后我们可以知道每件衣服自然蒸干的话能够蒸干t单元的水分,如果衣服本身含有水分小于等于t,那么这件衣服是不需要洗衣机的,如果是大于t的,那么大于t的部分是需要用洗衣机来蒸干的,相当于洗衣机每秒多蒸干k-1单元的水分,那么我们可以计算出该件衣服至少需要使用洗衣机多长时间,注意是上取整,最后计算出所有衣服占用洗衣机的时间和,如果大于t,那么说明我们枚举的时间偏小,否则说明时间可能偏大。按照这个思路进行二分即可。
需要注意一点,由于我们check函数中是除了k-1,那么k就不能等于1,所以k等于1时我们需要特判,k等于1那么洗衣机是不起作用的,直接取含水量最大的衣服的含水量作为答案即可。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e7+10;
int a[N];
int n,k;
bool check(int x)
{
//注意:这里可能会int溢出,所以应该将t设置为long long 类型
long long t=0;//记录每一件衣服所需要占用洗衣机的时间
for(int i=1;i<=n;i++)
{
if(a[i]<=x) continue;//不需要用洗衣机
t+=(a[i]-x-1)/(k-1)+1;//注意是上取整
}
return t<=x;
}
int main()
{
cin>>n;
int mx=0;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]),mx=max(mx,a[i]);
cin>>k;
if(k==1)//需要特判,因为当洗衣机流失水分速度等于自然流失速度,那么洗衣机将无法加速蒸干,而在check中会出现除0的操作
{
printf("%d",mx);
return 0;
}
int l=0,r=1999999999;
while(l<r)
{
int mid=l+r>>1;
if(check(mid)) r=mid;
else l=mid+1;
}
printf("%d",l);
return 0;
}G.POJ - 3258

样例输入:
25 5 2
2
14
11
21
17样例输出:
4题意:有一个长度为L的河,河的两端各有一块石头,在河中还有n块石头,给出每块石头的位置,现在让我们最多移除m块石头,不能移除河两端的石头,问相邻两块石头的距离的最小值最大可能是多少?
分析:一般看到最小值最大或者最大值最小问题就应该往二分思路上想,对于这道题目来说我们可以二分距离x,我们从河的一端开始考虑,找到离他最近的一块石头,如果两块石头之间距离小于x,那么就将这块石头移除,并统计移除的石头数目,如果两块石头之间的距离是大于等于x的,那么就保留这块石头,并将上一块未移除的石头位置标记为现在这个位置。我们每次判断一块石头是否应该移除都应该是与上一块未移除的石头之间求一个距离,判断这个距离和我们二分的x进行比较,小于x就移除,否则就直接更新上一块未移除的石头位置即可。最后我们需要比较移除的石头块和m的关系,如果小于等于m,代表当前距离是可行的,就将左边界更新一下,否则更新右边界。
注意由于给定的石头位置是无序的,所以我们首先需要对石头的位置进行排序。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e6+10;
int a[N];
int len,n,m;
bool check(int x)//二分间隔
{
int cnt=0;//记录达到最小间隔为x至少需要移走的石块数
int last=0;//记录上一块未移走的石头位置
for(int i=1;i<=n;i++)
{
if(a[i]-last<x)
cnt++;
else
last=a[i];
}
if(len-last<x) cnt++;//注意最后一块保留的石头与终点的石块距离也应大于等于x
return cnt<=m;//比较移走的石块数与m大小即可,小于等于m说明满足要求
}
int main()
{
cin>>len>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
sort(a+1,a+n+1);
int l=0,r=1e9+10;
while(l<r)
{
int mid=l+r+1>>1;
if(check(mid)) l=mid;
else r=mid-1;
}
printf("%d",l);
return 0;
} H.HDU - 6514

样例输入:
6 6
3
2 2 4 4
3 3 5 6
5 1 6 2
2
3 2 5 4
1 5 6 5样例输出:
YES
NO注意本题是多组输入!
题意:给定一个n和m代表地图的大小,接下来给定一个p代表监视器的数量,然后对于每一个监视器给定一个x1,y1,x2,y2代表这个监视器的可监视范围为以(x1,y1)和(x2,y2)为对角线顶点的矩形,最后给出一个q,代表询问组数,每次询问也是给出一个x1,y1,x2,y2,询问(x1,y1)和(x2,y2)为对角线顶点的矩形是否能被监视器完全监视。能输出YES,不能输出NO.
分析:相信大家都能够往差分上想,那么对于前面p个监视器的监视范围就相当于一个二维差分修改矩形值,那么我们处理完后就可以得到一个差分数组d,对这个差分数组d求一下前缀和我们就可以得到原数组,原数组的含义就代表每个位置会被多少个监视器监视,但是通过这道题我们可以发现我们只需要知道一个位置是否被监视而不需要知道他被多少个监视器所监视,所以我们对于原数组不为0的位置直接置为1即可。这样我们就可以知道每个位置是否被监视了,然后我们对原数组进行一次二维前缀和处理,这样我们就可以O(1)求出来一个面积内的格子被多少监视器监视了,由于每个格子最多被一个监视器监视,所以如果求出来的监视器个数不等于格子数,那么就说明一定有格子未在监视器监视范围内,直接输出NO,否则输出YES即可。
最后我们看一下数据范围:n*m<=1e7,给出这种形式我们无法具体确定n和m的范围,所以我们不能理解为n和m均为小于等于1e3.5的,所以这就代表了我们没法直接开二维数组来存这道题,所以我们需要用一个一维数组来存数据,每次需要用二维数据时我们只要对他进行一次映射即可。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e7+10;
int n,m;
int s[N];
int find(int x,int y)
{
if(x<1||y<1||x>n||y>m) return 0;//防止x等于0时出现(-1)*m+y
return (x-1)*m+y;
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF)//注意是多组询问
{
memset(s,0,sizeof s);
int p;
cin>>p;
int x1,y1,x2,y2;
for(int i=1;i<=p;i++)
{
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
s[find(x1,y1)]++;
s[find(x1,y2+1)]--;
s[find(x2+1,y1)]--;
s[find(x2+1,y2+1)]++;
}
for(int i=1;i<=n;i++)//将差分数组处理为原数组
for(int j=1;j<=m;j++)
s[find(i,j)]+=s[find(i-1,j)]+s[find(i,j-1)]-s[find(i-1,j-1)];
for(int i=1;i<=n;i++)//将原数组处理为前缀和数组
for(int j=1;j<=m;j++)
{
if(s[find(i,j)]) s[find(i,j)]=1;
s[find(i,j)]+=s[find(i-1,j)]+s[find(i,j-1)]-s[find(i-1,j-1)];
}
int q;
cin>>q;
for(int i=1;i<=q;i++)
{
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
int t=s[find(x2,y2)]-s[find(x1-1,y2)]-s[find(x2,y1-1)]+s[find(x1-1,y1-1)];//处理这一块矩形区域有多大面积被覆盖
if(t==(x2-x1+1)*(y2-y1+1)) puts("YES");
else puts("NO");
}
}
return 0;
}I.CodeForces - 371C

样例输入:
BBBSSC
6 4 1
1 2 3
4
样例输出:
2
题意:小明要做汉堡,汉堡由 'B' (bread), 'S' (sausage) ,'C' (cheese)组成,输入第一行给出汉堡的样式,第二行给出现有的B S C 的个数,第三行给出商店里B S C 的单价,第四行给出现有的钱数。问用这些最多能做出多少个汉堡。
分析:我们首先需要处理一下字符串,从字符串中我们可以求出来一个汉堡需要多少个B,多少个S以及多少个C。然后我们开始二分可以做出来的最多的汉堡数x,不妨假设一个汉堡需要cntB个B,cntS个S以及cntC个C,那么我们总共就需要cntB*x个B,cntS*x个S,cntC*x个C,那么由于我们已经有cntb个B,cnts个S,cntc个C,那么我们还需要买(cntB-cntb)个B,(cntS-cnts)个S,(cntC-cntc)个C,当然如果需要买的个数小于等于0那就代表不需要买,对于需要买的原料我们计算需要花费的钱的总和,如果小于等于所拥有的钱那么就可以做x个,否则就不可以,按照这个思路二分即可。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e3+10;
char s[N];
int cntB,cntS,cntC;
long long nb,ns,nc;
long long pb,ps,pc;
long long money;
bool check(long long x)
{
long long sum=0;//记录制作x个三明治至少要花多少钱
long long cntb=cntB*x-nb;//需要购买的面包数
long long cntc=cntC*x-nc;//需要购买的香肠数
long long cnts=cntS*x-ns;//需要购买的奶酪数
if(cntb>0) sum+=cntb*pb;//购买面包花的钱
if(cntc>0) sum+=cntc*pc;//购买香肠花的钱
if(cnts>0) sum+=cnts*ps; //购买奶酪花的钱
return sum<=money;//如果需要花费的钱少于拥有的钱就可以制作
}
int main()
{
scanf("%s",s+1);
for(int i=1;i<=strlen(s+1);i++)
if(s[i]=='B') cntB++;
else if(s[i]=='C') cntC++;
else cntS++;
cin>>nb>>ns>>nc>>pb>>ps>>pc>>money;
long long l=0,r=99999999999999;
while(l<r)
{
long long mid=l+r+1>>1;
if(check(mid)) l=mid;
else r=mid-1;
}
printf("%lld",l);
return 0;
}